厘清指數函數與冪函數離切交的位置關系
廣東省佛山市高明區第一中學(528500) 王順耿
引例已知函數f(x)=在其定義域(0,+∞)內既有極大值又有極小值,則實數a的取值范圍是( )
A.(0,1)∪(1,) B.(0,1) C.(,+∞) D.(1,)
因為f′(x)=x2?ax,要使函數f(x)在定義域(0,+∞)內既有極大值又有極小值,則導函數f′(x)有兩個變號零點,即函數y=x2與函數y=ax有兩個交點,探本溯源就是考察冪函數y=x2與指數函數y=ax圖象的位置關系.事實上,我們學習了指數函數和冪函數,但對它們間較為深入的函數圖象位置關系還缺少研究,明確它們間的位置關系對某些問題的研究有一定的幫助,下面對兩函數圖象的位置關系做進一步的探究.
1 指冪兩函數圖象的位置分析
指數函數y=ax(a >0,a≠1)圖象分布在第一、二象限,冪函數y=xα(α≠0)圖象主要分布在第一象限,當冪函數又是偶函數時,第二象限圖象與第一象限圖象對稱,下面依據底數a和冪指數α的變化,從三個角度對兩函數圖象的位置關系作深入探究.
1.1 確定的冪函數與變化的指數函數
冪函數y=xα(α≠0)的冪指數α確定,探究隨著指數函數y=ax(a >0,a≠1)底數a的變化,兩函數圖象的位置關系,先考察兩函數在(0,+∞)上的位置關系.

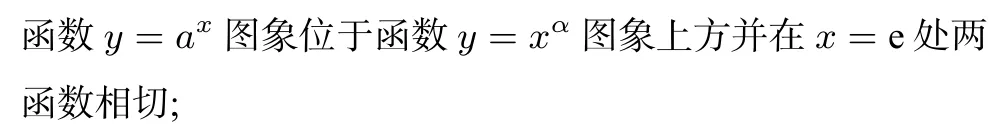
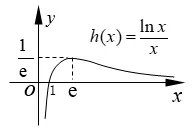
③若0 ④若lna <0,則0< a <1,函數y=lna與函數f(x)=相交一點,方程ax=xα一解,在(0,+∞)上,函數y=ax圖象與函數y=xα圖象在x=x0(x0∈(0,1))處相交. ⑧若lna >0,則a >1,函數y=lna與函數f(x)=相交一點,方程ax=xα一解,在(0,+∞)上,函數y=ax圖象與函數y=xα圖象在x=x0(x0∈(0,1))處相交. 特別地,當冪函數y=xα又是偶函數時,在(?∞,0)上,指數函數y=ax圖象與冪函數y=xα圖象的位置關系探究如下: 由a?x=(?x)α=xα(x >0,x≠1),得=?lna,同樣令f(x)=. (1)當α>0 時,據圖1 有以下結論: 圖1 ①當?lna >,即0< a <(<1)時,a?x >(?x)α,在(?∞,0)上,函數y=ax圖象在函數y=xα圖象上方; ②當?lna=,即a=(<1)時,在(?∞,0)上,函數y=ax圖象位于函數y=xα圖象上方并在x=?e 處兩函數相切; ③當0 ④當?lna <0,即a >1 時,在(?∞,0)上,函數y=ax圖象與函數y=xα圖象在x=∈(?1,0))處相交. (2)當α<0 時,據圖2 有以下結論: 圖2 ⑤當?lna <,即a >(>1)時,a?x <(?x)α,在(?∞,0)上,函數y=ax圖象在函數y=xα圖象下方; ⑥當?lna=,即a=(>1)時,在(?∞,0)上,函數y=ax圖象位于函數y=xα圖象下方并在x=?e 處兩函數相切; ⑧當?lna>0,即0 指數函數y=ax(a >0,a≠1)的底數a確定,探究冪函數y=xα(α≠0)隨著冪指數α的變化,兩函數間的位置關系,先考察兩函數在(0,+∞)上的位置關系. (1)當a >1 時,lna >0,x=e 是函數g(x)在(1,+∞)上的極小值點,也是(1,+∞)上的最小值點,g(x)min=g(e)=e lna >0,如圖3 所示,依圖3 有下面結論: 圖3 ①若α <0,函數y=α與函數g(x)=相交一點,方程ax=xα一解,在(0,+∞)上,函數y=ax圖象與函數y=xα圖象在x=x0(x0∈(0,1))處相交; ②若0< α ③若α=e lna,函數y=α與函數g(x)=相切,在(0,+∞)上,函數y=ax圖象位于函數y=xα圖象上方并在x=e 處相切; ④若α >e lna,函數y=α與函數g(x)=相交兩點,在(0,+∞)上,函數y=ax圖象與函數y=xα圖象在x=x1(x1∈(1,e))和x=x2(x2∈(e,+∞))處相交. (2)當0< a <1 時,lna <0,x=e 是函數g(x)在(1,+∞)上的極大值點,也是(1,+∞)上最大值點,g(x)max=g(e)=e lna <0,如圖4 所示,依圖4 有下面結論: 圖4 ⑤若α >0,函數y=α與函數g(x)=相交一點,在(0,+∞)上,函數y=ax圖象與函數y=xα圖象在x=x0(x0∈(0,1))處相交; ⑥若e lna < α <0,有< α(x >1)和> α(0< x <1),即ax < xα(x >0),在(0,+∞)上,函數y=ax圖象在函數y=xα圖象下方; ⑦若α=e lna,函數y=α與函數g(x)=相切,在(0,+∞)上,函數y=ax圖象位于函數y=xα圖象下方并在x=e 處相切; ⑧若α 同樣地,給定指數函數y=ax,當冪函數y=xα又是偶函數時,在(?∞,0)上,冪函數y=xα圖象與指數函數y=ax圖象的位置關系,探究如下: 由a?x=(?x)α=xα(x >0,x≠1),得=?α,同樣令g(x)=. (1)當a>1 時,據圖3 有以下結論: ①當?α<0,即α>0 時,在(?∞,0)上,函數y=xα圖象與函數y=ax圖象在處相交; ②當0?α(x >1)和0),在(?∞,0)上,函數y=xα圖象在函數y=ax圖象上方; ③當?α=e lna,即α=?e lna時,在(?∞,0)上,冪函數y=xα又是偶函數時,其函數圖象位于指數函數y=ax圖象上方并在x=?e 處相切; ④當?α >e lna,即α (2)當0 ⑤當?α>0,即α<0 時,在(?∞,0)上,冪函數y=xα圖象與指數函數y=ax圖象在處相交; ⑥當e lna 1)和>?α(0< x <1),即a?x > xα=(?x)α(x >0),在(?∞,0)上,冪函數y=xα圖象在指數函數y=ax圖象下方; ⑦當?α=e lna,即α=?e lna時,在(?∞,0)上,冪函數y=xα又是偶函數時,其函數圖象位于指數函數y=ax圖象下方并在x=?e 處相切; ⑧當?α 當冪指數α=底數a時,探究指數函數y=ax(a >0,a≠1)與冪函數y=xa(a >0,a≠1)的位置關系,先考察在(0,+∞)上的位置關系. 由ax=xa,得,令h(x)=,由h′(x)==0,得x=e 是函數h(x)在(0,+∞)上的極大值點,也是最大值點,h(x)max=h(e)=,如圖5 示,依圖5 有下面結論: 圖5 ④若?<0,則>0,由圖5 可得a >1,在(?∞,0)上,冪函數y=xα圖象與指數函數y=ax圖象在x=∈(?1,0))處相交. 這樣,就將指數函數與冪函數離切交的位置關系進行了完整地探究,綜合上述探究,還可以得出一個一般性的結論: 若指數函數y=ax(a>0,a≠1)與冪函數y=xα(α≠0)在(0,+∞)上相切,必在x=e 處相切;在(?∞,0)上相切,必在x=?e 處相切. 例1 見文首“引例”. 解由1.1 中的③得,當1< a <時,函數y=ax圖象與函數y=xα圖象在x=x1(x1∈ (1,e))和x=x2(x2∈(e,+∞))處交叉相交,故選D. 例2 已知不等式在(0,+∞)上恒成立,則t的取值范圍是____. 解由1.2 中的⑥、⑦得,當e ln≤t+1<0,即?(1+e ln 3)≤t 依據1.3 中的函數h(x)=及圖5 可得結論: 題4 (2015年高考山東文科第3題)設a=0.60.6,b=0.61.5,c=1.50.6,則a,b,c的大小關系是( ) A.a C.b 解據上面結論,顯然為b 例5 比較與與πe的大小 解據上面結論,顯然有 仔細體會上述的探究方法及其結論,當我們碰到需要考慮指數函數與冪函數位置關系的問題時,就可以汲取上述的研究方法或結論,以便快速方便地去解決相關指冪函數間的問題.
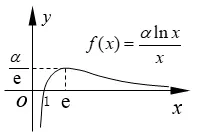
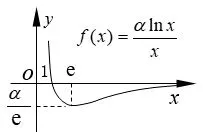
1.2 確定的指數函數與變化的冪函數

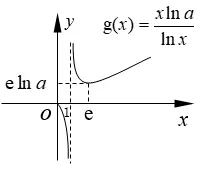

1.3 底數a 與冪指數α 同步變化


2 簡單應用


