探尋凹凸本質 凝煉致用模型

東莞市第四高級中學(523220) 王文濤

一.試題呈現

題目1 (2021年廣東省中考第25題節選)二次函數y=ax2+bx+c的圖像過點(?1,0),且對任意實數x,都有4x?12≤ax2+bx+c≤2x2?8x+6,求該二次函數的解析式.

題目2 (2020年高考江蘇卷第19題節選)已知關于x的函數y=f(x),y=g(x)與h(x)=kx+b(k,b∈R)在區間D上恒有f(x)≥h(x)≥g(x),若f(x)=x2+2x,g(x)=?x2+2x,D=(?∞,+∞),求h(x).

這兩道題的形式新穎,表面看起來考察的是二次函數恒成立問題,但實質背景是凹凸函數的切線方面的幾何特征.下面從一元函數微分學的視角給出新的解答和推廣.

二.解法探究

以題目1 為例,采用兩邊夾的思想,先必要性求值,再證明充分性.

解因為二次函數y=ax2+bx+c的圖像過點(?1,0),所以有a?b+c=0.又因為對任意實數x,都有4x?12≤ax2+bx+c≤2x2?8x+6,令x=3,有0≤9a+3b+c≤0,所以9a+3b+c=0,與a?b+c=0聯立,解得b=?2a,c=?3a.

設f(x)=4x?12,g(x)=ax2+bx+c,h(x)=2x2?8x+6,則f(x)≤g(x)≤h(x),f(3)=g(3)=h(3).設F(x)=g(x)?f(x)=ax2+(b?4)x+c+12,F′(x)=2ax+b?4,由上知F(x)≥0=F(3),則x=3 是F(x)的極小值點,由費馬引理得F′(3)=0,即2a×3+b?4=0,所以a=1,b=?2,c=?3.

下證充分性.當a=1,b=?2,c=?3,g(x)?f(x)=x2?6x+9=(x?3)2≥0,h(x)?g(x)=x2?6x+9=(x?3)2≥0,所以f(x)≤g(x)≤h(x),所以所求的解析式為y=x2?2x?3.

注f(x)=4x?12 是g(x)與h(x)在x=3 處的公切線.

三.相關背景

為行文方便起見,以下根據文獻[1]給出函數凸(凹)的定義以及相關定理和幾何特征.

定義1 設f為定義在區間I上的函數,若對I上的任意兩點x1,x2和任意實數λ∈(0,1),總有f(λx1+(1?λ)x2)≤λf(x1)+(1?λ)f(x2),則稱f為I上的凸函數.反之,如果總有f(λx1+(1?λ)x2)≥λf(x1)+(1?λ)f(x2),則稱f為I的凹函數.

定理1 設f為定義在區間I上的可導函數,則下述論斷互相等價:1?f為I上的凸(凹)函數; 2?f′為I上的增(減)函數;3?對I上的任意兩點x1,x2,有f(x2)≥f(x1)+f′(x1)(x2?x1)(f(x2)≤f(x1)+f′(x1)(x2?x1)).

定理2 設f(x)為區間I上的二階可導函數,則在I上f為凸(凹)函數的充要條件是f′′(x)≥0(f′′(x)≤0),x∈I.

通過以上論斷3?我們能得到凸(凹)函數的幾何特征:凸(凹)函數的曲線總是在它的任一切線的上方(下方).

四.三種推廣模型

性質1 設f(x)和g(x)為開區間I上的二階可導函數,f(x)≥g(x),f(x0)=g(x0),且滿足下列三個條件之一:(1)f(x)為凸函數,g(x)為凹函數;(2)f(x)為凸函數,g(x)為凸函數;(3)f(x)為凹函數,g(x)為凹函數,則f(x)和g(x)必存在公切線h(x),且對應三個條件有(1)f(x)≥h(x)≥g(x);(2)f(x)≥g(x)≥h(x);(3)h(x)≥f(x)≥g(x).

證明設F(x)=f(x)?g(x),由條件知F(x)≥0=F(x0),則x0為函數F(x)的極小值點,由費馬引理得F′(x0)=0,即f′(x0)=g′(x0),又因為f(x0)=g(x0),所以f(x)和g(x)在x=x0處存在公切線h(x).后略.

以上三個條件對應了三種推廣模型,分別見圖1(對應例1)、圖2(對應題目1)、圖3(對應例2).

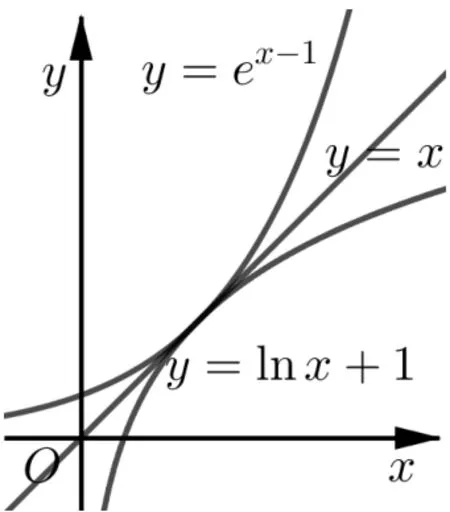
圖1

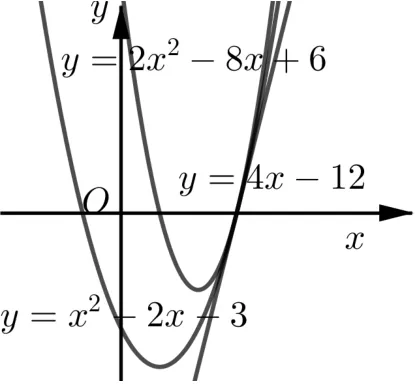
圖2

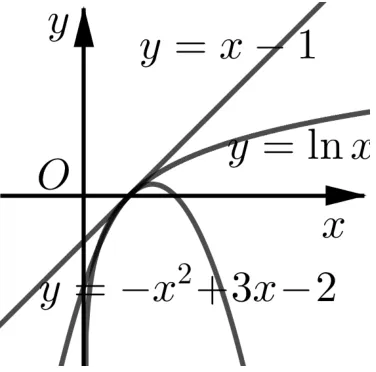
圖3

五.典型例題

例1 已知f(x)=ex?1,g(x)=lnx+1 與h(x)=kx+b(k,b∈R)在區間(0,+∞)上恒有f(x)≥h(x)≥g(x),求h(x)的表達式.

解由ex?1≥kx+b≥ lnx+1,令x=1,得1≥k+b≥1,所以k+b=1.設G(x)=ex?1?(kx+b),G′(x)=ex?1?k,滿足G(x)≥0=G(1),則由費馬引理有G′(1)=0,即1?k=0,所以k=1,b=0.下證充分性.當k=1,b=0,G(x)=ex?1?x,G′(x)=ex?1?1,當x∈(0,1),G′(x)<0; 當x∈(1,+∞),G′(x)>0,所以G(x)≥G(1)=0,所以ex?1≥x.設H(x)=x?(lnx+1),H′(x)=.當x∈(0,1),H′(x)<0;x∈(1,+∞),H′(x)>0,所以H(x)≥H(1)=0,所以x≥lnx+1,所以f(x)≥h(x)≥g(x).因此h(x)=x.

注解題的核心是先觀察或分析出是否存在x0使得f(x0)=g(x0).

例2 已知當x≥,?x2+3x?2≤klnx+m≤x?1,求k,m.(答案:k=1,m=0)

例3 (重慶南開中學試題節選)已知f(x)=x2,g(x)=blnx.定義:對于函數f(x)與g(x)定義域上的任意實數x,若存在常數k,m,使得f(x)≥kx+m,g(x)≤kx+m都成立,則稱直線y=kx+m為函數數f(x)與g(x)的“隔離直線”.設b=2e,試探究f(x)與g(x)是否存在“隔離直線”?若存在,求出“隔離直線”的方程;若不存在,請說明理由.(答案:存在;y=

解決如例3 這樣新定義概念的題型更需要一雙“慧眼”.

六.指導意義

三種推廣模型及蘊含的思想方法也可以引導我們突破問題.

例4 (2021年八省聯考第22題)已知函數f(x)=ex?sinx?cosx,g(x)=ex+sinx+cosx.(1)證明:當時,f(x)≥0.(2)若g(x)≥2+ax,求a.

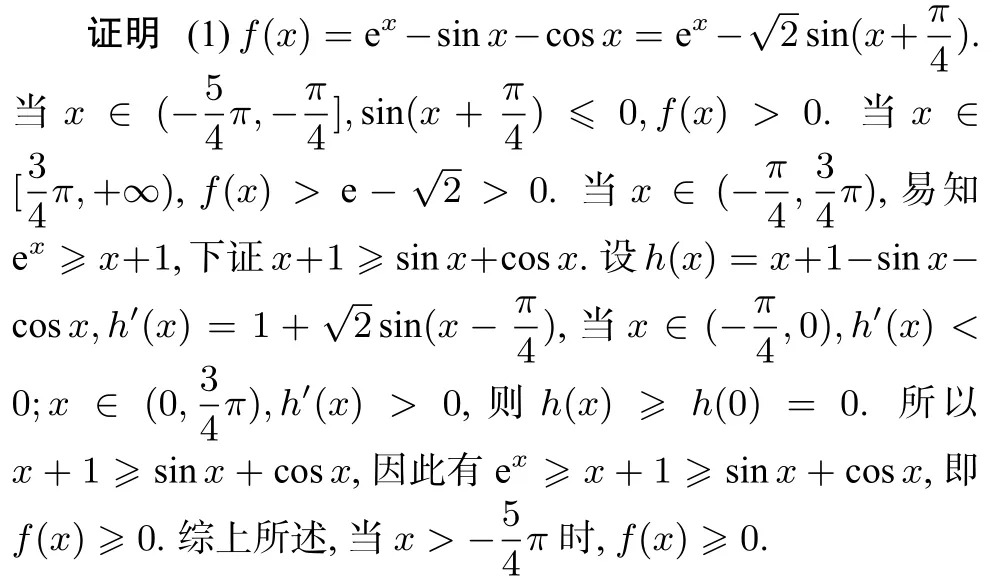
(2)設φ(x)=ex+sinx+cosx?ax?2≥0=φ(0),所以φ′(0)=0,因為φ′(x)=ex+cosx?sinx?a,所以φ′(0)=1+1?0?a=0,即a=2.充分性的證明從略.

思路剖析第(1)問注意到m(x)=ex是凸函數,n(x)=sinx+cosx,n′′(x)=,當x∈,n′′(x)<0,此時n(x)是凹函數.又m(0)=n(0)=1,m′(0)=n′(0)=1,因此m(x)和n(x)在x=0處有公切線y=x+1,故考慮分類討論:在x∈部分用切線放縮的模型來做,其余兩部分根據三角函數值的周期性和有界性去討論,見圖4.第(2)問也用到了觀察法和先必要性求值再證明充分性的方法.值得一提的是g(x)和y=2+ax均過(0,2),g′′(x)=ex?sinx?cosx=f(x),由第(1)知當x >?π時,g′′(x)≥0,所以第(2)問的命題有凸函數(局部)的切線放縮的背景.由上述分析也可以對本題做以下改編.

圖4

改編題(1)已知:當x∈(?,+∞),有ex≥kx+b≥sinx+cosx成立,求k,b.(答案:k=b=1)

(2)若ex+sinx+cosx≥kx+b≥2 ln(x+1)+2 對任何實數x成立,求k,b.(答案:k=b=2)

注在模型f(x)≥h(x)≥g(x)中,若f(x)恒大于g(x),則上述方法失效,需要分兩步f(x)≥h(x),h(x)≥g(x)來做,比如2020年高考江蘇卷第19題第(2)(3)問.

眾多高考題出題的背景涉及到凹凸函數的切線性質,又因為高中所涉及到的函數一般都具有二階導數,所以在教學中可以高屋建瓴地適當引導學生通過二階導數值的正負快速判斷函數在某一區間的凹凸性,而一旦具有凹凸性,便可嘗試利用其良好的切線性質作為解題的突破口.本文不拘泥于以二次函數為載體,而是對其推廣到一般的凹凸函數;推廣的模型可以指導解決問題并改編和命制題目(比如例4),體現了創新性.