探究一道以卡特蘭數為背景的概率題

安徽省淮南第二中學(232001) 趙帥

一、原題呈現

(淮南第二中學屆高三模擬)某中學為了豐富學生的課外生活,減輕學生的生活壓力,組織學生開展以班級為單位的猜謎語比賽,規定每班的初始分為0 分,隨機抽取題目,猜對得5 分,猜錯扣5 分,并且猜測結果只有“對”與“錯”兩種,設高二年級某班學生猜對的概率為,猜錯的概率為,記“該班學生完成n次猜謎語后的總分為Sn”.若規定積分扣到零分則被淘汰(第一次輸也會被淘汰),求S5=5 的概率.

解析S5=5,即總共猜謎語5 次,猜錯2 次,又由Si≥5(i=1,2,3,4),可得共有以下可能:

①第一次和第二次猜對,第三次猜錯,第四次猜對,第五次猜錯;

②第一次、第二次和第三次猜對,其余兩次猜錯.故所求概率為:

二、問題一般化與變式

易知,若猜謎語的次數為奇數,則猜正確和猜錯誤的次數中二者必為一奇數一偶數,則最后的得分必為5 的奇數倍;若猜謎語的次數為偶數,則猜正確和猜錯誤的次數中二者必為兩奇數或兩偶數,則最后的得分必為5 的偶數倍.

在滿足規定:積分扣到零分則被淘汰(第一次猜錯也會被淘汰)的情況下,則S2n+1=5×(1+2m)=10m+5(m,n∈N)與S2n=5×2m=10m(m,n∈N?)概率為多少?

分析要解決這個問題,先從解決S5=5 的概率入手.我們可建立一個坐標“棋盤”,為了簡潔,縱坐標為得分的.如圖1.

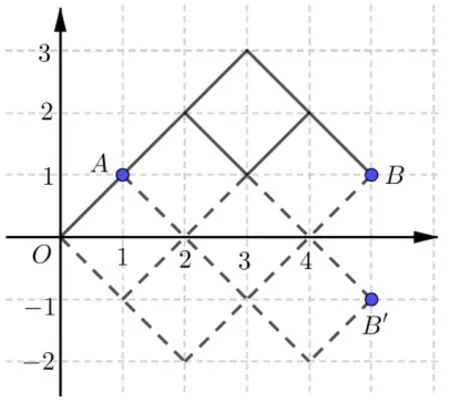
圖1

首先,初始情況對應圖中O點,由于第一次猜謎語一定要贏,則必須到達A(1,1)點,然后沿著最短路徑到達B(5,1)點(過程中必有兩次正確兩次錯誤).顯然符合規定的路徑條數有且只有兩條,故所求概率為:

顯然這種解法易于觀察,但對于研究更一般的情形很難解決.所以對解法做出以下調整.

若不考慮規定,則從A點到B的最短路徑數為=6,但很顯然6 條最短路徑中并不是每個都符合規定(即路徑要在x軸上方),為此,取B′(5,?1),則可發現,不滿足規定的A點到B點所有經過x軸的最短路徑與A點到B′點所有最短路徑為一一對應的關系,則它們的路徑數相同,故不符合規定的最短路徑數為=4.故所求概率為

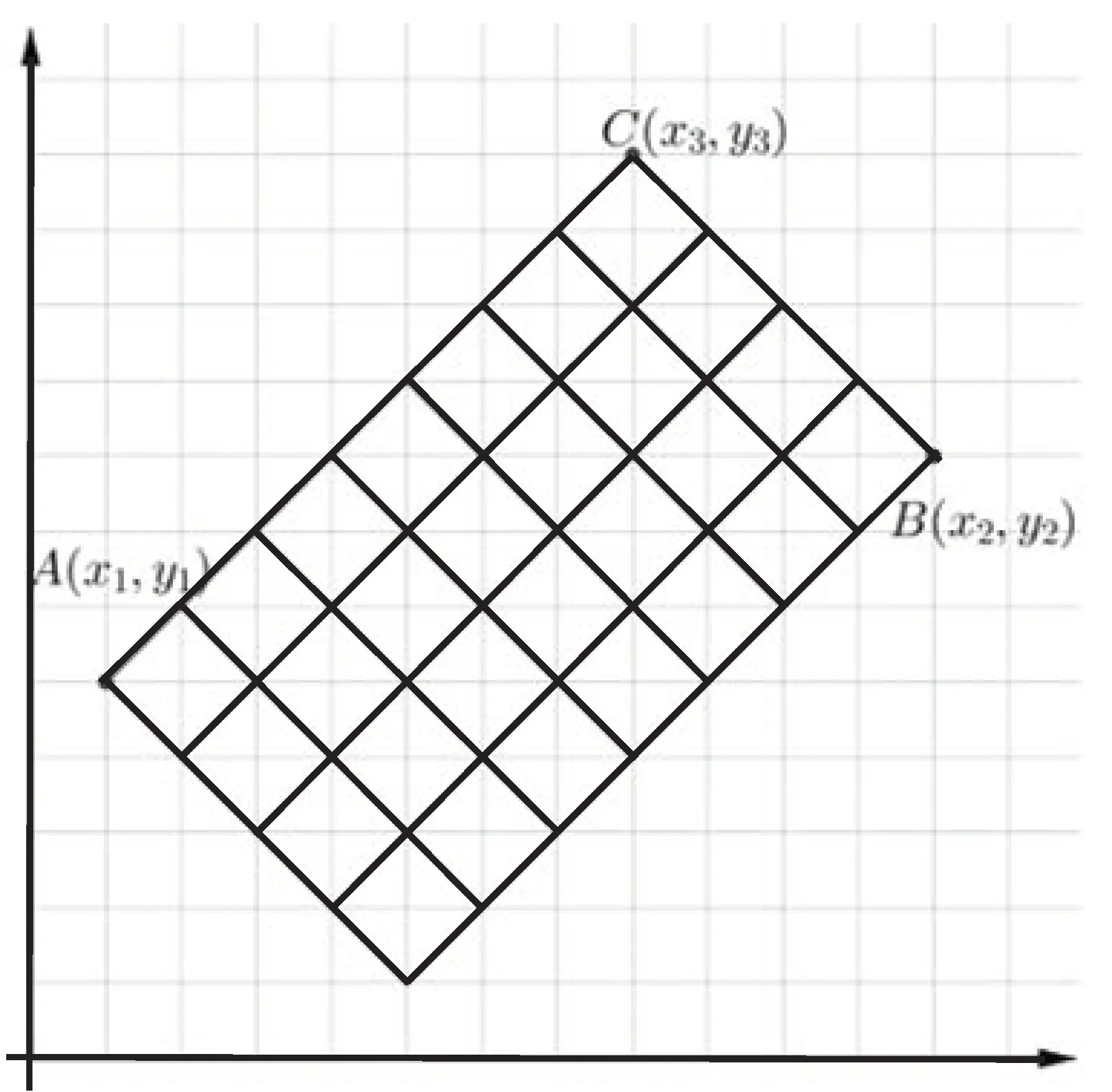
圖2

據此,我們根據以上分析可得以下定理,并證明之.

定理1 由整點A(x1,y1)到整點B(x2,y2)的所有最短路徑條數為

證明可知直線AC的方程為:y?y1=x?x1,直線BC的方程為:y?y2=?(x?x2),解得C點坐標為,故由點A到點C需要經過x3?x1=次步驟,同時也為共x2?x1步驟中所有“上升”的步驟數.由組合知識可得,由整點A(x1,y1)到整點B(x2,y2)的所有最短路徑條數為

定理2 由整點A(x1,y1)到整點B(x2,y2)(其中y1>0,y2>0,x2?x1≥y1+y2)圖象恒在x軸上方(不含x軸)的所有最短路徑條數為

證明由定理1 可知,為整點A(x1,y1)到整點B′(x2,?y2)(點B關于x軸的對稱點)的所有最短路徑數.即證由整點A(x1,y1)到整點B(x2,y2)圖象經過x軸所有最短路徑數等于由整點A(x1,y1)到整點B′(x2,?y2)的所有最短路徑數.設P為由點A到點B所有經過x軸的最短路徑構成的集合,P′為由點A到點B′所有最短路徑構成的集合,即證|P|=|P′|.下證P與P′為一一映射.

設由點A到點B的最短路徑中與x軸的第一個交點為點M,則由點M到點B的路徑與由點M到點B′的路徑均關于x軸對稱,且剩余路徑均相同,顯然P與P′為一一映射,故|P|=|P′|,定理成立.

變式1 若積分扣到零分則被淘汰(第一次猜錯也會被淘汰),求S9=15 的概率.

解設猜對的次數為x,猜錯的次數為y,則有x+y=9且x?y=3 解得x=6,y=3.由于規定,則需求出從(1,1)點到(9,3)點的最短路徑條數與(1,1)點到(9,?3)點的最短路徑條數之差,則可通過構造棋盤得:

變式2 若積分扣到零分則被淘汰(第一次猜錯也會被淘汰),求S2n+1=10m+5(m,n∈N)與S2n=10m(m,n∈N?)的概率.

解對于S2n+1=10m+5(m,n∈N),設猜對的次數為x,猜錯的次數為y,則有x+y=2n+1 且x?y=2m+1 解得x=m+n+1,y=n?m.由于規定,則需求出從(1,1)點到(2n+1,2m+1)點的最短路徑條數與(1,1)點到(2n+1,?2m?1)點的最短路徑條數之差,則可通過構造棋盤得:同理,對于S2n=10m(m,n∈N?),可得:

三、鏈接高考并推廣

題目(2016年高考全國Ⅲ卷)定義“規范01 數列”{an}如下:{an}共有2m項,其中m項為0,m項為1,且對任意的k≤2m,a1,a2,···,ak中0 的個數不少于1 的個數.若m=4,則不同的“規范01 數列”共有( )

A.18個 B.16個 C.14個 D.12個

解記每項取1 得1 分,取0 扣一分.則此“規范01數列”的個數為:由(1,1)點到(8,0)點且圖象恒在直線y=?1 圖象上方的最短路徑條數,構造棋盤,也即:由(1,2)點到(8,1)點且圖象恒在x軸上方的最短路徑條數,即:

推廣定義“規范01 數列”{am+n} 如下:{am+n}共有m+n項,其中m項為1,n項為0,且對任意的k≤m+n(m≥n),a1,a2,···,ak中0 的個數不少于1的個數,求不同的“規范01 數列”個數.

解記每項取1 得1 分,取0 扣一分.則此“規范01 數列”的個數為:由(1,1)點到(m+n,m?n)點且圖象恒在直線y=?1 圖象上方的最短路徑條數,也即:由(1,2)點到(m+n,m?n+1)點且圖象恒在x軸上方的最短路徑條數,即:

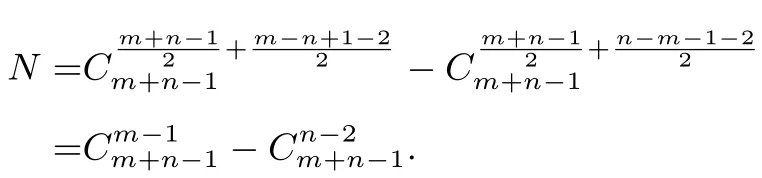
綜上,再進行深入研究可知問題的結論背景直指組合數學中的“卡特蘭數”(組合數學中一個常出現在各種計數問題中的數列,其在出棧次序問題,凸多邊形三角劃分問題,信息學中有很多得應用).我們可通過構造棋盤模型,將原本復雜的問題變為更為具體清晰,為解決這類概率(計數)問題提供了便利.