三穩態電磁式渦激振動俘能裝置發電性能研究

吳子英， 常宇琛， 趙 偉， 李永越， 劉麗蘭

(西安理工大學 機械與精密儀器工程學院,西安 710048)

流致振動現象初期研究重心主要集中在如何抑制流致振動對高聳建筑物海洋結構物[1-2]的危害，如廣東虎門大橋也受到了流致振動的危害。此外，科學界也對流致振動現象進行開發利用，提出了基于流致振動的能量捕獲裝置，較為典型是基于渦激振動和馳振的能量捕獲裝置，基于流致振動的能量捕獲研究也成為了能量捕獲領域的熱點話題[3-4]。

較為成功的最早研究渦激振動能量捕獲裝置的是美國密歇根大學Bernitsas等[5]提出的渦激振動能量發電裝置VIVACE，該裝置利用海洋洋流流經圓柱體時，引發圓柱體產生渦激振動從而帶動電磁感應式轉子發動機發電來捕獲流體動能，成功開創了人類在海洋洋流能量利用中的里程碑。渦激振動能量捕獲裝置多樣，多采用壓電懸臂梁連接圓柱形鈍體型結構，如宋汝君等[6]提出的復擺式渦激振動俘能器，分別從理論和實驗角度研究了水流流速與俘能功率之間的關系。羅竹梅等[7]提出了串列、并列和錯列布置的耦合連接型五圓柱柱體結構渦激振動俘能器，獲得了柱群俘能結構集中俘獲低速海流能的初步理論。在結構參數影響研究方面，白旭等[8]分析了低阻尼條件下不同質量比對渦激振動能量捕獲效率的影響。曹東興等[9]從理論和實驗角度較為詳細的研究了流速、圓柱體直徑、磁間距、磁極和外接電阻等系統參數對俘能器振動特性及輸出電壓的影響。

目前的渦激振動俘能裝置多可以簡化為線性振動系統，共振帶寬過窄；相較于線性振動，非線性振動因具有較寬的工作帶寬，所以基于非線性振動的俘能裝置受到了國內外學者的廣泛關注。如Ma等[10]針對如何提高非線性頻寬做了大量研究；首次使用了兩段線性彈簧建立非線性系統使得俘能裝置在過渡區域也可使用，提出了自適應非線性剛度理念；實驗證明，此裝置可在水速0.275 m/s以上充分俘能，俘能效率較傳統的線性系統有較大提升。Qin等[11]建立了渦激振動和馳振復合振動裝置(BPEH)，引入雙穩態系統進一步提高俘能效率；該裝置在全流速范圍內，渦激振動和馳振相互發揮耦合作用，可以適應復雜激勵的流速場。譚洪波等[12]提出了一種多穩態馳振能量捕獲器，對其動力學響應和發電性能進行了數值仿真研究；三、四穩態系統有較淺的勢阱，在較小的外界激勵能量下，系統易產生大幅運動模式。

本文將彈簧提供的三穩態特征與電磁式渦激振動能量發電裝置相結合，提出了一種三穩態電磁式渦激振動俘能裝置，通過引入單向離合器校正發電機輸入軸的轉動方向，使用三相交流電磁發電機實現能量轉換，通過數值仿真分析非線性系統參數對發電性能的影響規律，分析能量俘獲裝置結構參數、單向離合器以及飛輪大小對渦激振動俘獲裝置發電性能的影響規律。

1 三穩態渦激振動俘能裝置和力學模型

1.1 三穩態渦激振動俘能裝置模型

渦激振動是由于流體黏性作用使得其在繞流圓柱體后側產生了交替脫落的漩渦，從而引起了柱體橫向的往復運動，如圖1所示。

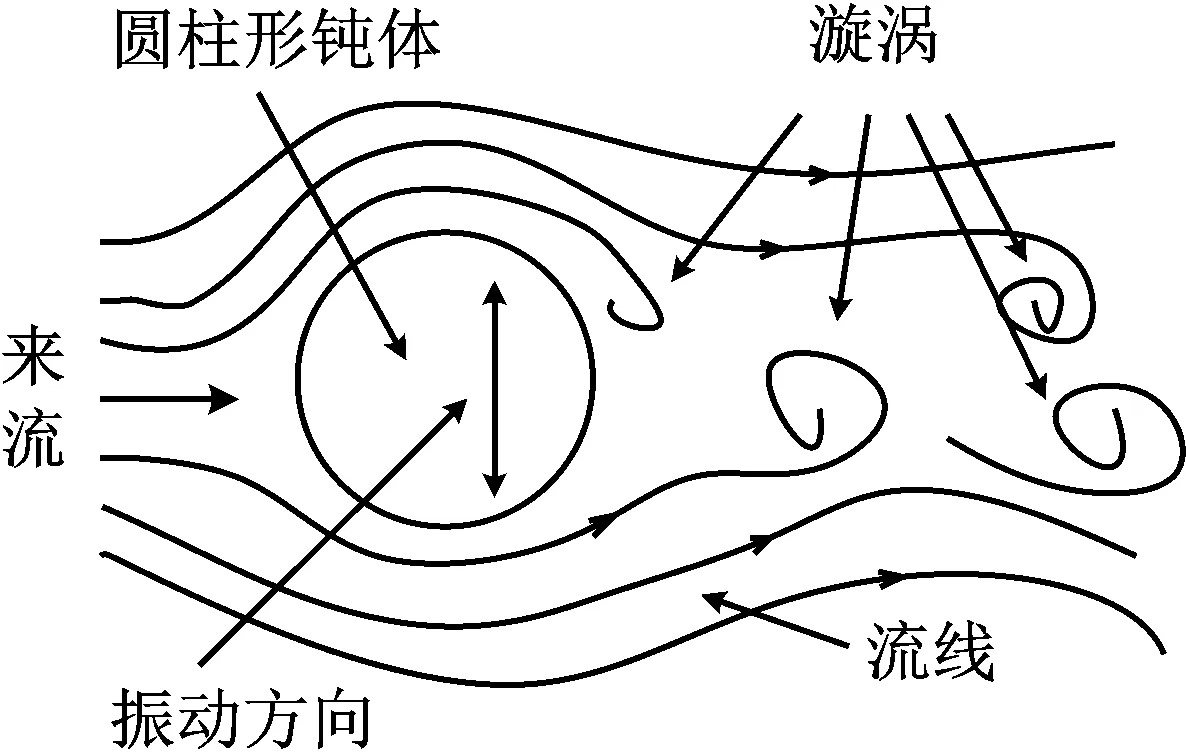
圖1 渦激振動原理示意圖Fig.1 Schematic of vortex induced vibration

本文通過引入非線性回復力和單向離合器，提出的一種可進行鈍體上下兩個振動方向動能捕獲的新型三穩態電磁式渦激振動俘能裝置，如圖2所示。圖2中，在中心軸6上左側安裝有左齒輪4、正向單向離合器14，中心軸6右側安裝有右齒輪7、反向單向離合器13，左/右齒輪分別通過正向/反向單向離合器與中心軸6相連，中心軸6借助聯軸器12與發電機11和飛輪10相連，鈍體1固定在鈍體支架15末端，鈍體支架15在直線導軌3中上下滑動，左右齒輪同時與鈍體支架相連，彈簧2安裝在鈍體支架15與機架5間。圓形截面鈍體1在水流的沖擊下產生上下運動，當鈍體1向上運動時，鈍體支架15帶動左齒條17和右齒條16同時向上運動，由于正向/反向單向離合器工作方式不同，正向單向離合器14工作，此時，反向單向離合器13不工作，從而左齒條17帶動與其嚙合的左齒輪4轉動，而右齒輪8不發生轉動，左齒條17、左齒輪4、正向單向離合器14通過中心軸6將鈍體1的向上直線運動轉換為驅動轉子發電機11發電的旋轉運動。當鈍體1向下運動時，右齒條16驅動右齒輪7轉動，反向單向離合器13工作，正向單向離合器14不工作，此時左齒輪4空轉，右齒輪7將鈍體1向下的直線運動轉換為驅動轉子發電機11發電的旋轉運動。在水流的沖擊下，鈍體1上下運動，發電機11始終朝著一個方向轉動。

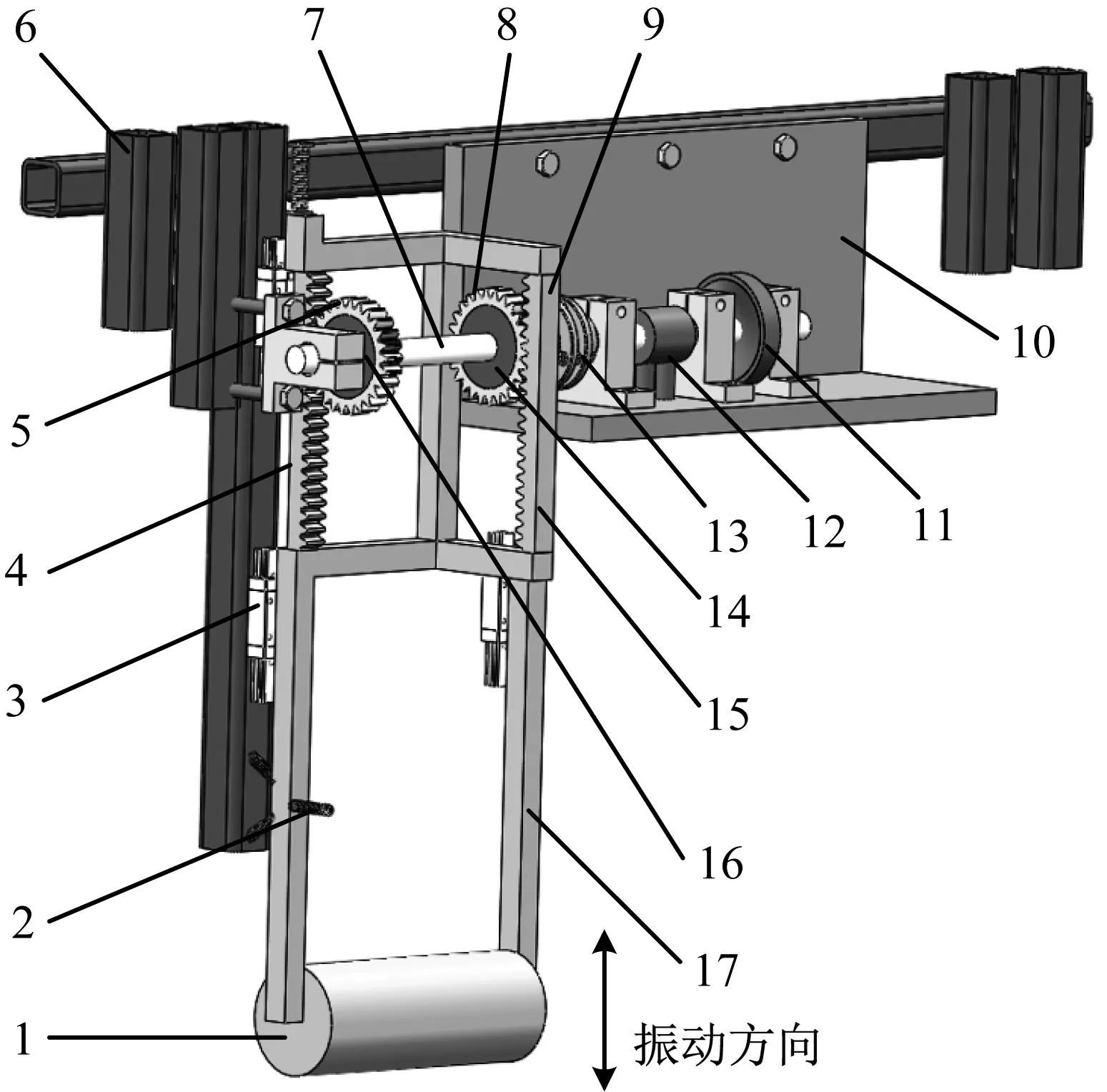
1-圓形截面鈍體；2-彈簧；3-直線導軌；4-左齒條；5-左齒輪；6-機架；7-中心軸；8-右齒輪；9-右齒條；10-固定板；11-飛輪；12-轉子發電機；13-聯軸器；14-反向單向離合器；15-右齒條；16-正向單向離合器；17-鈍體支架圖2 三穩態渦激振動俘能裝置模型Fig.2 3D model of tristable vortex induced vibration energy harvester

1.2 非線性回復力

本文的非線性回復力建模借助Yang等[13]的思想，如圖3所示。

圖3中，中心慣性質量M由一個水平支撐彈簧和一對斜彈簧支撐，具有Ks(N/m)剛度的彈簧起到了恢復機構的作用；當外部激勵作用于M(鈍體)時，鈍體以y(t)方向振動。雖然每個彈性構件都提供線性恢復力，但由于幾何構型的關系，產生的力具有很強的非線性。是非線性系統的幾何參數，其a,b,c,l為彈簧的正常狀態長度。采用質量M來決定整個系統的質量，因其質量遠大于彈性構件的質量，故彈簧的動質量總和可以忽略不計。

對于給定的位移，非線性系統的彈性勢能Us表達式如下：

(1)

(2)

選取參數a=0.07 m、b=0.02 m、c=0.015 m、Ks=200 N/m、l=0.05 m，由式(1)可得出勢能函數如圖4，可看出具有明顯的三穩態特征。

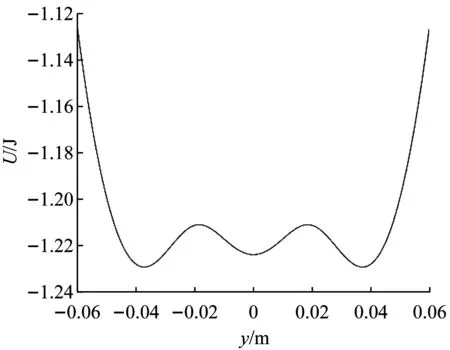
圖4 三穩態系統勢能圖Fig.4 Tristable potential energy function

1.3 尾流振子方程

Hartlen等[14]最早提出了流固耦合的尾流振子模型，把流場近尾跡動力學用振子來模化；采用Van der Pol方程來描述近尾跡流場的振蕩特性，計算得到了正確的升力變化規律。Facchinetti等[15]在流固耦合模型中分別采用結構的位移、速度和加速度來耦合并表示流體振子的運動過程，通過對比計算，認為采用加速度描述振子的受力最為理想。本文亦采用加速度項來描述本文發電裝置的流固耦合現象，Van der Pol尾流振子的方程為

(3)

式中：q為無量綱參數，意為尾流振子；ε為非線性項中的小參數；A為結構對流體的耦合動力參數。尾流振子無量綱參數q定義為

(4)

式中:CL是流體對結構的瞬時升力系數；CL0是對應的靜態圓柱體橫向升力幅值；Ωf表示漩渦脫落頻率

(5)

式中：U為流體的流速；D為剛性圓柱體的外徑；St為斯特勞哈爾數。

1.4 三穩態渦激振動俘能裝置力學模型和動力學方程

該渦激振動俘能裝置由兩部分構成：水流和非線性彈簧支承的鈍體相互耦合作用而構成的尾流振子系統；單向離合器、齒輪與轉子式發電機構成的轉子發電系統。對圖1所示結構模型進行力學簡化，將圓形鈍體和齒條簡化為如圖5所示的集總質量。

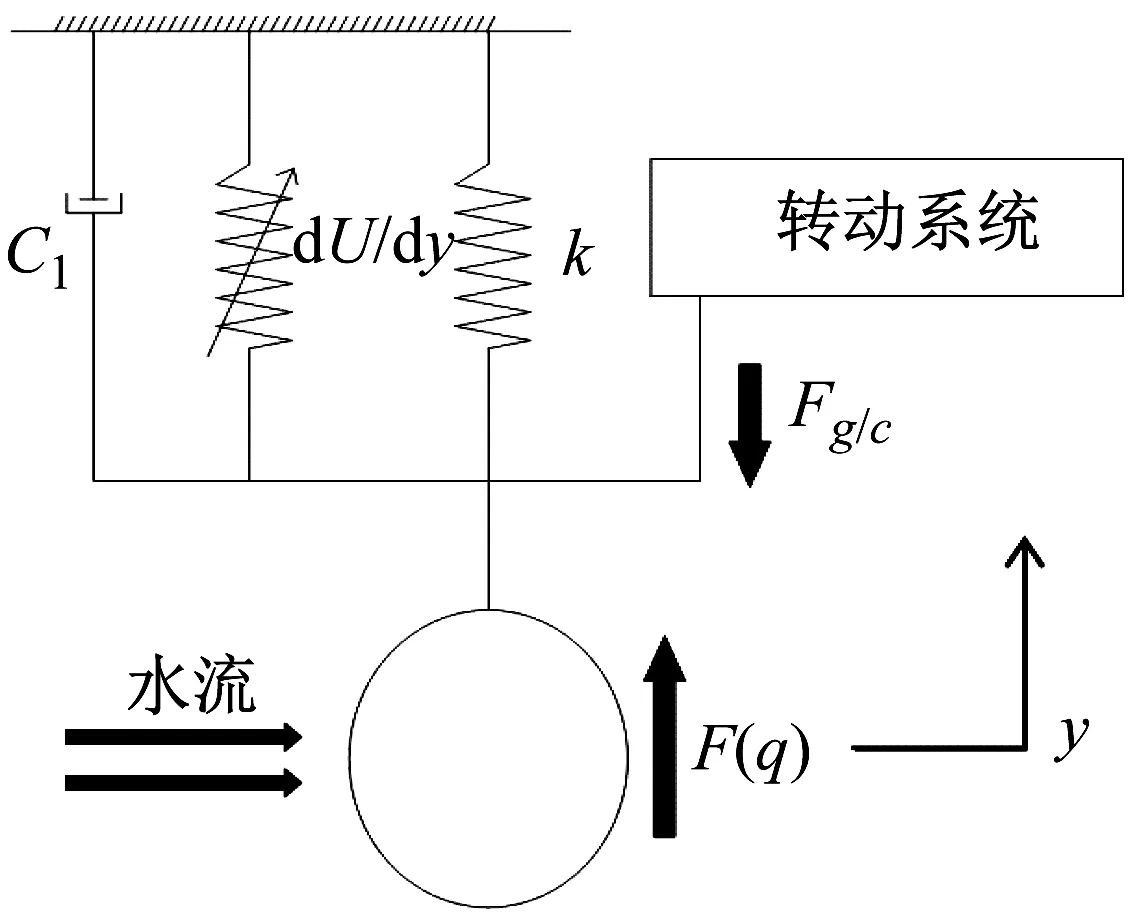
圖5 鈍體系統力學模型Fig.5 Mechanical model of bluff vibration system

根據牛頓第二定律和尾流振子方程，可以得到直徑為D的單自由度非線性彈簧支承的剛性鈍體在自由流速度為U的平穩勻速流動中的動力學方程為

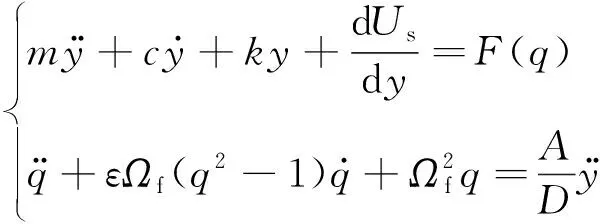
(6)

式中：m為剛性圓柱體質量和流體附加質量，即m=ms+ma；ms為圓柱體質量；ma為流體附加質量，即ma=1/4CmρπD2L；Cm為附加質量系數；ρ為流體密度；c為結構阻尼cn和流體阻尼cf之和，c=cn+cf；cf為流體阻尼，cf=γΩfρD2；F(q)為水流激勵力，F(q)=1/4ρU2DCL0Lq；L為鈍體長度。

1.5 轉子系統力學模型和動力學方程

將齒輪、單向離合器、轉子發電機和飛輪部分簡化為如圖6所示的轉子系統模型。

圖6 轉子系統力學模型Fig.6 Schematic of nonlinear restoring force

在轉子系統工作過程中，由于鈍體上下振動的速度變化，導致左/右齒輪的轉速也發生變化，發電機也處于運轉狀態，此時會出現兩種工作狀態：① 左/右齒輪轉速大于發電機的轉速，鈍體的動能能量通過齒輪、單向離合器到發電機，轉化為電能，此時鈍體和發電機處于結合狀態；② 左/右齒輪轉速小于發電機的轉速，由于單向離合器只有在輸入轉速大于輸出轉速時才起作用[16]，所以鈍體的動能能量無法通過齒輪、單向離合器到發電機，此時鈍體和發電機處于脫離狀態。因此需要將上述兩種狀態分別進行建模研究。

在結合狀態下，水流力F(q)通過鈍體和單向齒輪結構傳遞到發電機，發電機產生阻力

(7)

綜上，得到結合狀態下三穩態渦激振動俘能裝置流固電耦合的動力學方程為

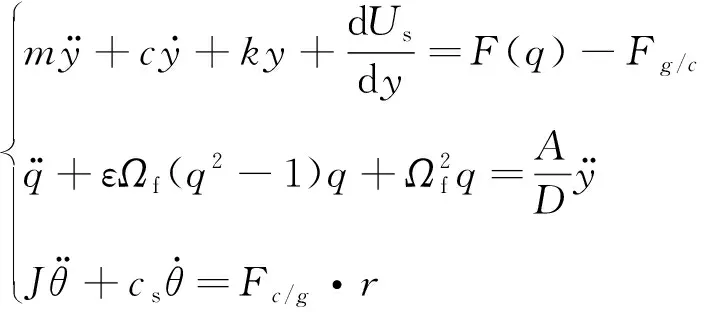
(8)

式中：Fg/c是發電系統對鈍體系統的阻力，與此同時也是發電系統的動力，所以Fg/c和Fc/g大小相同，方向相反；J是齒輪、中心軸、發電機和飛輪的總轉動慣量；Cs是發電系統的阻尼系數；r為齒輪半徑。

根據法拉第感應定律得到角位移引起電動勢的電壓UVIV

(9)

進一步可得到俘能裝置的發電功率表達式P

(10)

式中：ke為電勢系數；RL為發電機外電阻；Ra為發電機內電阻。

(11)

式(11)的解可寫為

θ=θ0e-(ceq/J)t

(12)

式中:θ0為發電機的最大轉速;t為衰減時間。因此，脫離周期的阻尼力和輸出電壓為

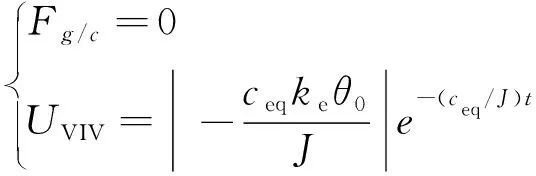
(13)

綜上，得到脫離狀態下，三穩態渦激振動俘能裝置流固電耦合的動力學方程為

(14)

2 數值仿真

相對于雙穩態勢能函數，三穩態勢能函數具有3個穩定平衡點和2個不穩定平衡點，勢阱深度較雙穩態淺，在較弱的外界激勵下三穩態系統通常更易產生大幅運動模式。單向離合器結構具有速度相反運動校正功能，從而使本文的俘能裝置具有更高的發電效率。主要從以下兩個方面進行數值仿真研究：① 將三穩態渦激振動俘能裝置與雙穩態渦激振動俘能裝置發電性能對比，探究三穩態能量捕獲器的特點；② 研究俘能裝置結構參數對發電功率的影響規律，探尋俘能裝置較佳結構參數配置；探討有無單向離合器與飛輪大小對發電性能的影響。仿真參數如表1所示。

表1 仿真參數Tab.1 Simulation parameters

2.1 雙穩態與三穩態俘能裝置發電功率和動力學響應比較

2.1.1 勢能函數比較

三穩態和雙穩態的勢能函數如圖7所示。

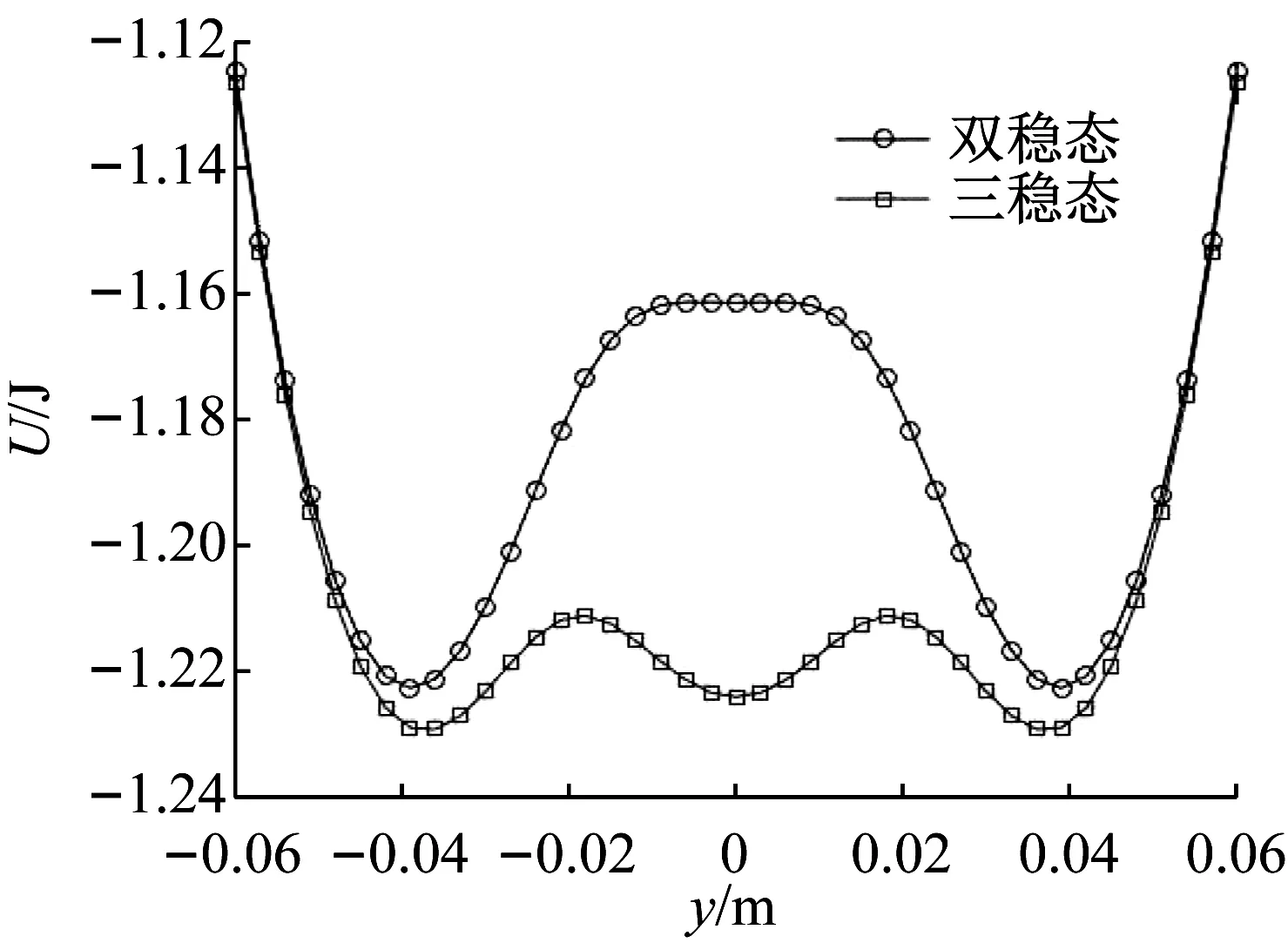
圖7 兩種穩態系統勢能函數對比Fig.7 Bistable and tristable potential energy function

由圖7可知：雙穩態俘能器具有兩個對稱勢阱和一個勢壘，而三穩態俘能器具有三個勢阱和兩個勢壘。從圖中得出雙穩態俘能器的勢壘高度-0.062 J，而三穩態俘能器的勢壘高度僅為-0.033 J，差值為0.029 J。即三穩態系統較雙穩態系統勢壘顯著降低，在相同的外界激勵下，三穩態俘能器可以更容易地越過勢壘，實現大幅度運動。

2.1.2 振幅比和發電功率

在流致振動研究中，通常采用振幅比(A*)來描述鈍體的位移幅度，振幅比(A*)被描述為實際位移與鈍體的半徑的比值，即：

A*=y/D

(15)

兩種系統的振幅比和發電功率如圖8所示。

由圖8可知:① 在引入三穩態系統之后，在振幅比的峰值數值高于雙穩態系統；且無論是雙穩態或是三穩態系統，都會隨著流速的繼續增加而減小；這是因為鈍體采用圓柱體，發生“渦激振動”現象；渦激振動顯著的特點是較低流速下產生渦激共振使發電裝置的振動幅值最大，且存在“自限性”現象;② 隨著流速的增加，兩種俘能系統功率的變化曲線同樣遵循渦激振動的“自限性”現象：在流速為0.32 m/s時，取到最大值，隨后流速再增加，功率減小；三穩態系統不僅在峰值高于雙穩態，且降低的速率也明顯慢于雙穩態。說明從發電性能來看，三穩態系統遠遠優于雙穩態系統。通過與文獻[9]的研究結果相比，本文的仿真研究結果與文獻[9]的研究結果有相似性，也證明了本文的結果有一定的正確性。

綜上，可得出部分結論：① 引入雙穩態和三穩態后，阻流體的振動均出現了在一定流速范圍內，隨著流速的增大而增大的趨勢，且之后出現了“自限性”現象；② 相對于雙穩態，引入三穩態后的鈍體隨著流速的增大，其振幅比增大的幅度較大；且發電功率都有明顯的提升，說明三穩態系統較雙穩態系統來說有更優良的發電性能。

2.1.3 動力學響應

為了進一步分析振幅比情況，我們選取圖8曲線中三個速度點U=0.22 m/s，U=0.32 m/s和U=0.42 m/s，得到鈍體的相圖與振幅比圖，如圖9～圖11所示。

從圖9、圖10和圖11可以看出，在三個流速的情況下，雙穩態和三穩態俘能裝置鈍體的增大速度大小基本一致，但與雙穩態俘能裝置，三穩態俘能裝置的鈍體振幅比更大。

根據式(5)可以計算出三種流速0.22 m/s、0.32 m/s和0.42 m/s的漩渦脫落頻率分別為0.44、0.63和0.83 Hz，對式(6)進行掃頻數值仿真，得到三穩態渦激振動俘能系統中鈍體的振動幅值響應曲線，如圖12所示。

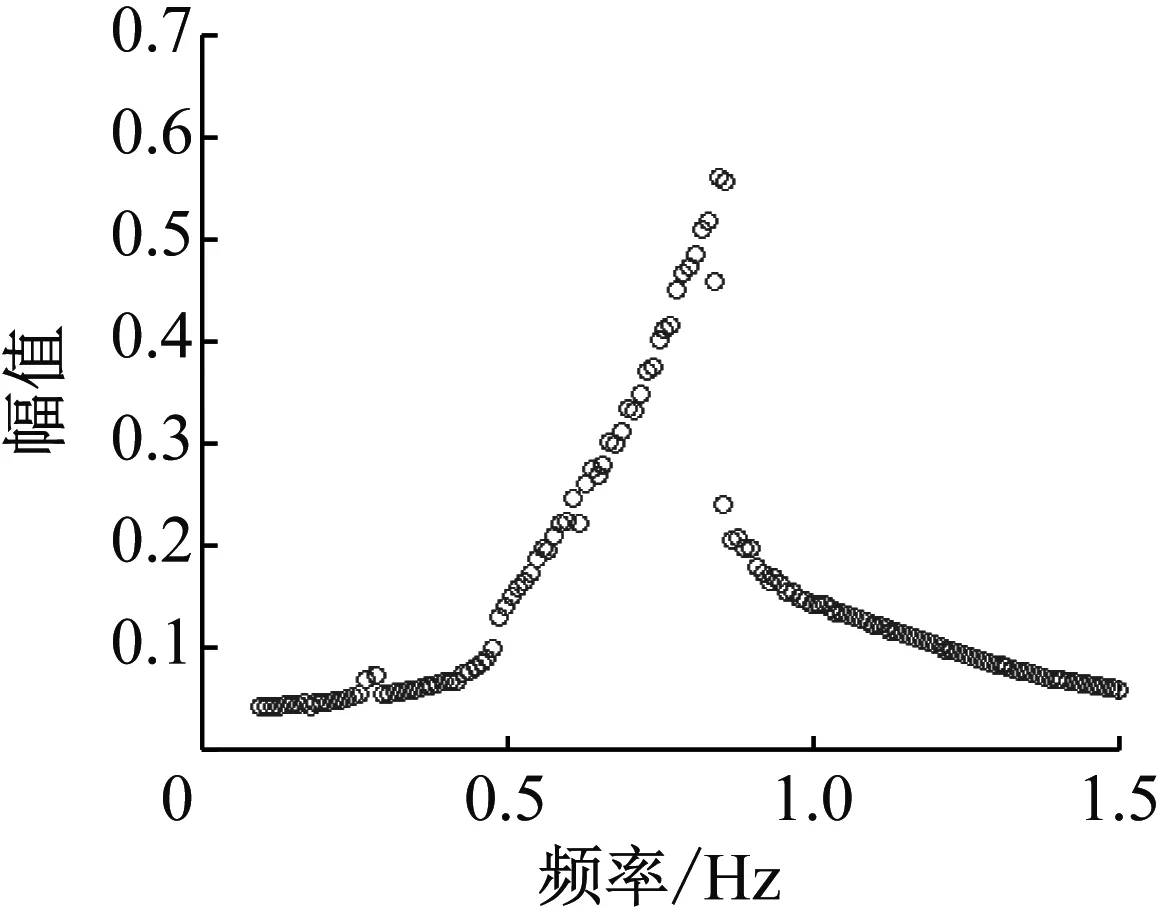
圖12 非線性幅頻響應曲線Fig.12 Nonlinear Relationship curve of vibration amplitude of TVIVEH vs. frequency

從圖12可以看出，文中三穩態渦激振動俘能裝置具有非線性振動特征，共振頻帶較寬，漩渦脫落頻率也位于非線性共振頻帶中，隨著漩渦頻率的增大，俘能系統非線性振動的幅值也隨之增大，從0.8左右振幅有所下降，側面驗證了理論建模的正確性。

2.2 質量比對系統的影響

質量比m*的定義為鈍體的結構質量與其排開水的流體質量之比，數學表達如式(16)所示

(16)

分別取質量比m*=1.02,1.27，1.66,1.91；其他參數分別取值為D=100 mm，RL=10 Ω；四個質量比下俘能裝置發電功率的仿真結果如圖13所示。

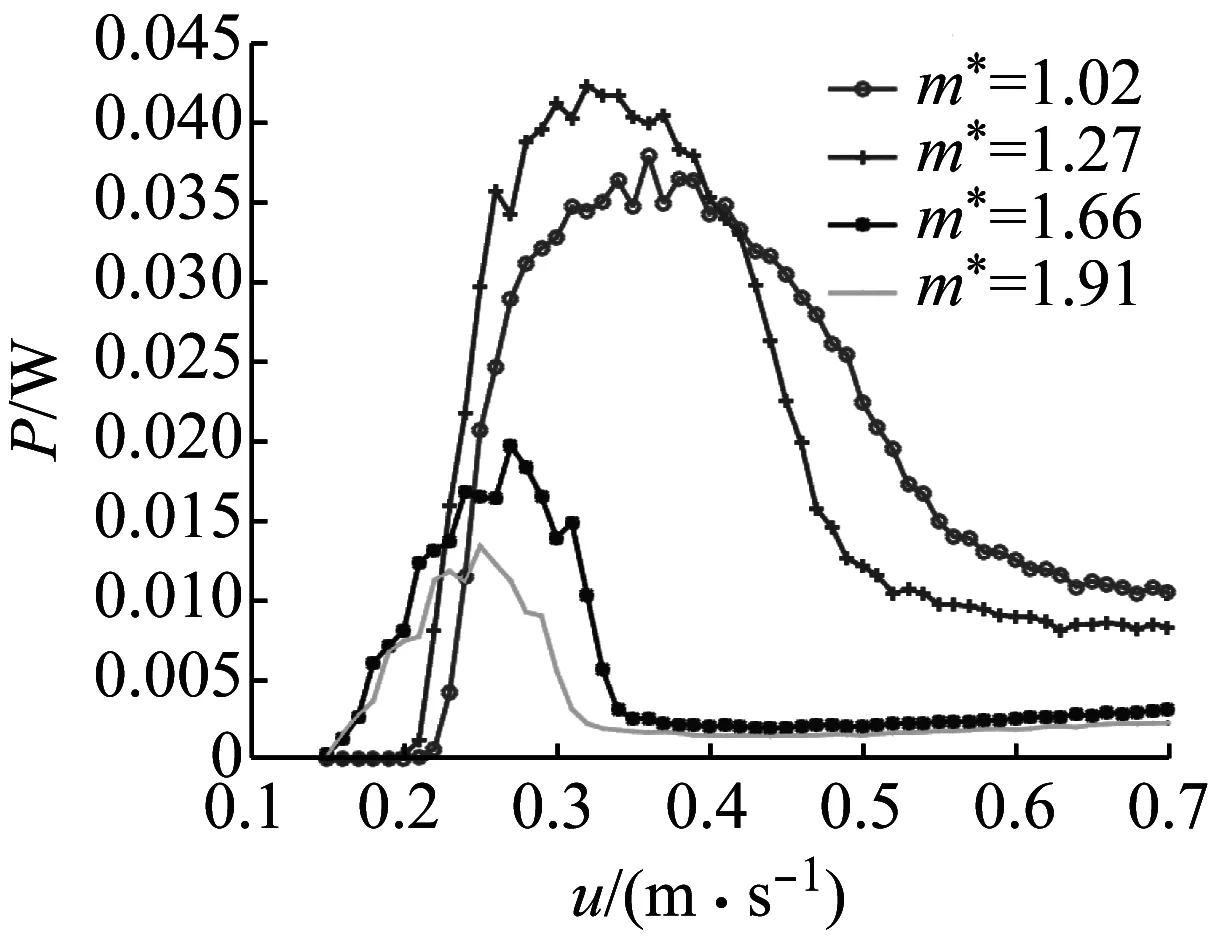
圖13 不同質量比下功率隨流速變化曲線Fig.13 Relationship curve of power of TVIVEH vs. water velocity under different mass ratio

從圖13可以看出，三穩態渦激振動能量俘能器系統在不同質量比下平均功率趨勢均為快速增長然后下降趨勢；且當質量比大于1.27時，隨著質量比的增加，俘能裝置的發電功率在不斷減小。說明質量比為1.27時，俘能裝置發電性能較佳。

2.3 鈍體直徑對系統的影響

鈍體直徑主要影響渦激振動的渦脫頻率和尾流鈍體q，因此鈍體直徑的選取要在適宜的范圍內，取鈍體直徑90 mm，100 mm，110 mm和120 mm，根據圖13，其他關鍵參數分別取值為m*=1.27，RL=10 Ω；四個鈍體直徑下俘能裝置發電功率的仿真結果如圖14所示。

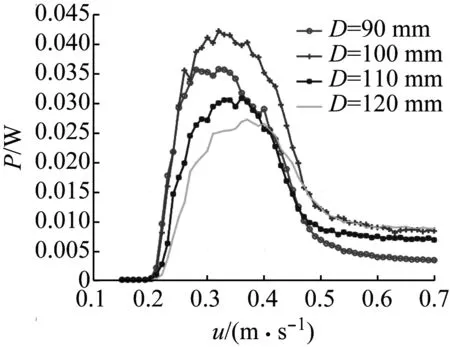
圖14 不同鈍體直徑下功率隨流速變化曲線Fig.14 Relationship curve of power of TVIVEH vs. water velocity under different diameter of bluff

從圖14可以看出，三穩態渦激振動能量俘能器系統在不同鈍體直徑下其平均功率趨勢均為快速增長然后下降趨勢；且當直徑大于100 mm時，隨著直徑的增加，發電功率在不斷減小。

為了準確分析鈍體直徑對裝置發電性能的影響規律；取U=0.32 m/s時，分析不同的鈍體直徑對于發電性能的影響，如圖15所示。

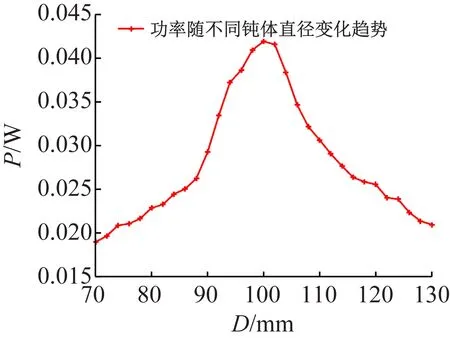
圖15 不同鈍體直徑裝置發電功率曲線Fig.15 Relationship curve of power vs. diameter of bluff

由圖14和圖15可知，在質量比m*=1.27直徑為100 mm時，該系統的鈍體直徑可獲得最大發電量。

2.4 負載電阻對系統的影響

三穩態渦激振動電磁式發電裝置的發電系統的電阻主要分為發電機內阻(Ra)和負載電阻(RL)；發電機內阻是隨發電機不同而固定的數值，而本節則是在探究不同的負載電阻對裝置的發電性能特性有何影響；分別取RL=5 Ω，10 Ω，15 Ω，20 Ω，其他關鍵參數分別取值為m*=1.27，D=100 mm；四個負載電阻下俘能系統的發電功率如圖16所示。

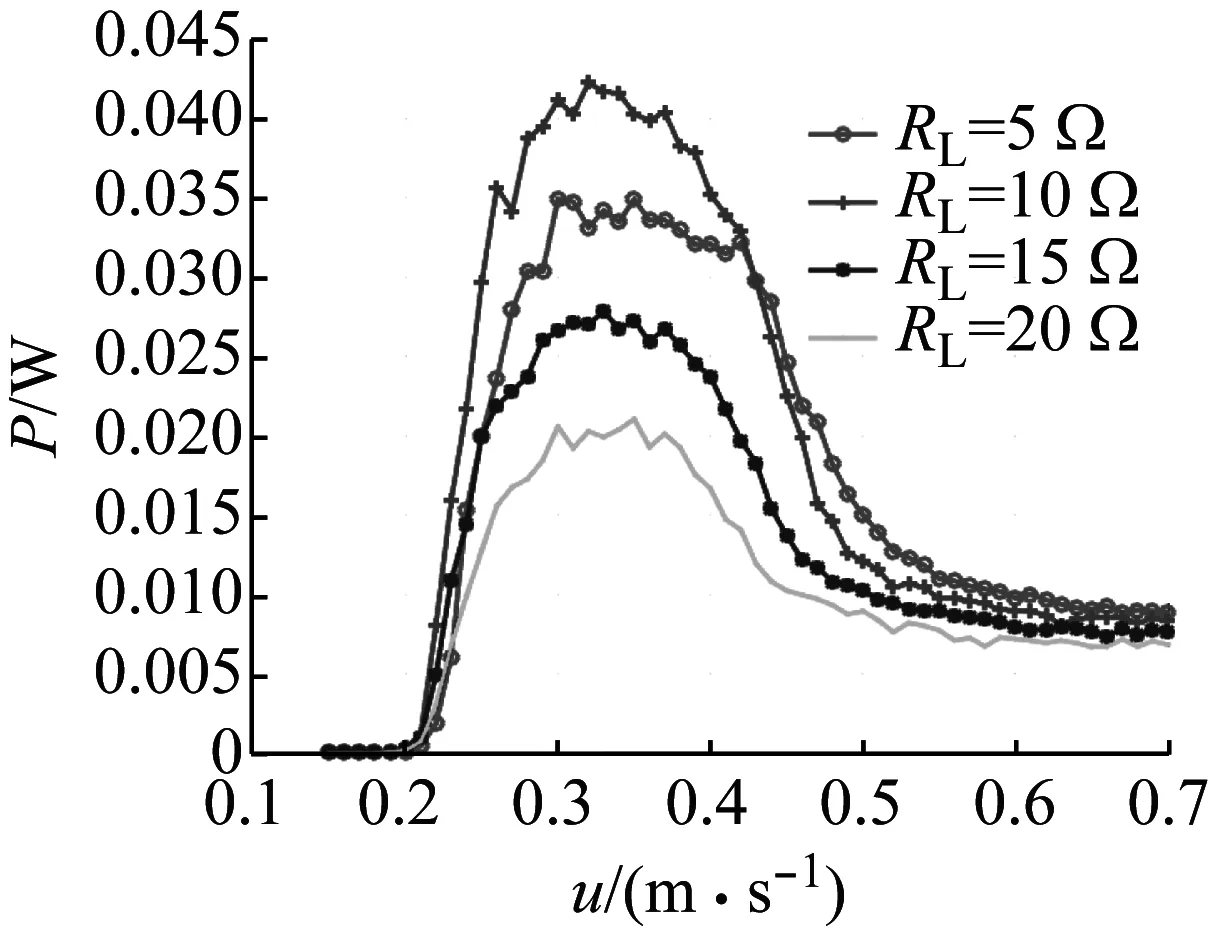
圖16 不同負載電阻下功率隨流速變化曲線Fig.16 Relationship curve of power of TVIVEH vs. water velocity under different load resistance

由圖16可知，三穩態渦激振動能量俘能器系統在不同負載電阻下平均功率趨勢均為快速增長然后下降趨勢；且當負載電阻大于10 Ω時，隨著負載電阻的增加，發電功率在不斷減小。

為了準確分析負載電阻對裝置發電性能的影響規律；取U=0.32 m/s時，保持質量比參數1.27和直徑參數100 mm不變，分析不同的負載電阻對于發電性能的影響，如圖17所示。

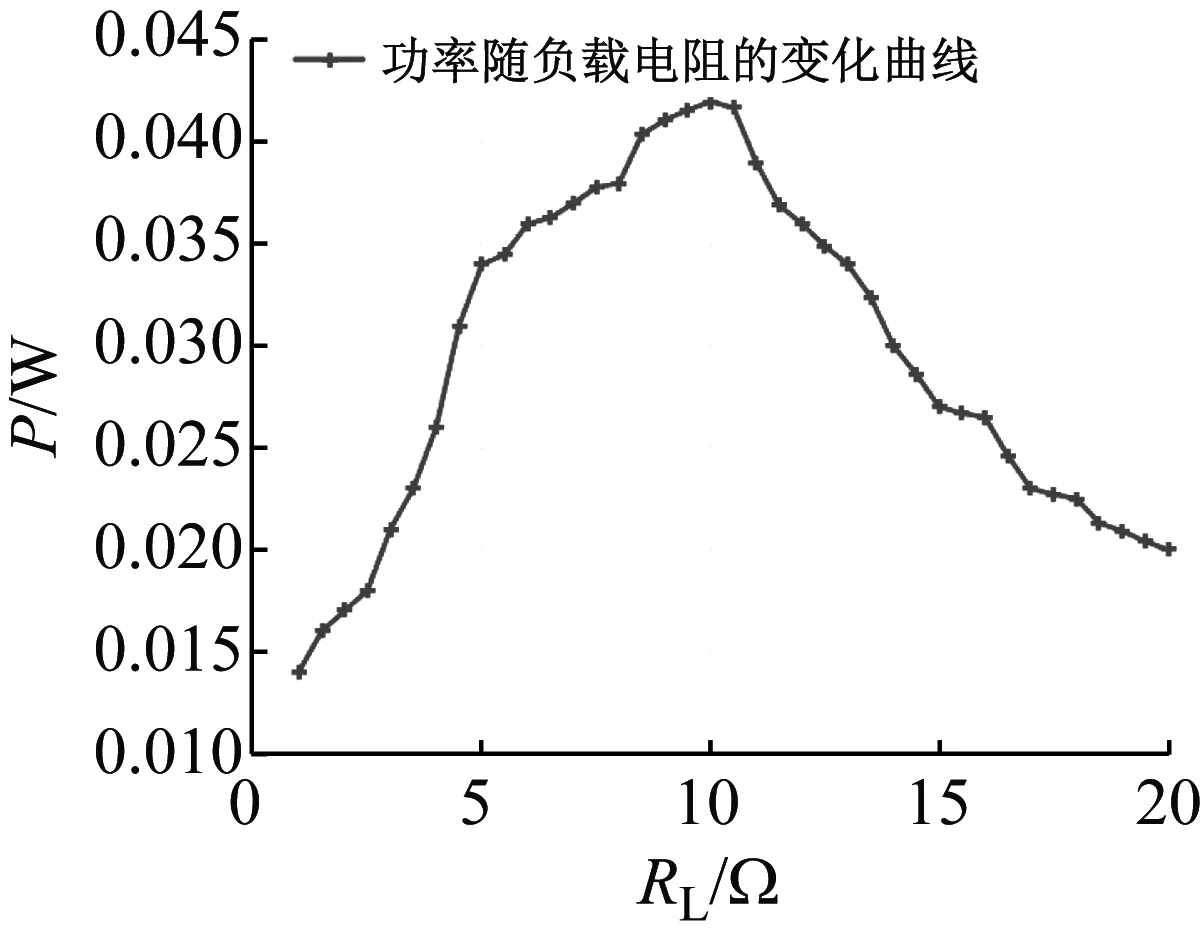
圖17 不同負載電阻裝置發電功率曲線Fig.17 Relationship curve of power vs. load resistance

由圖16和圖17可知，負載電阻為10 Ω時，俘能裝置輸出功率最大，該負載電阻值為該系統的最優參數。

2.5 單向離合器和飛輪大小的影響

飛輪是利用自身轉動慣量來吞吐能量，從而減少發電機轉速的速度波動，使輸出功率更平穩。分析有/無單向離合器(記為MMR/No-MMR)時，俘能裝置發電功率變化情況，同時也給出了兩種不同轉動慣量(即0.000 7 kg·m2和0.000 2 kg·m2)飛輪下的發電功率情況，如圖18所示。

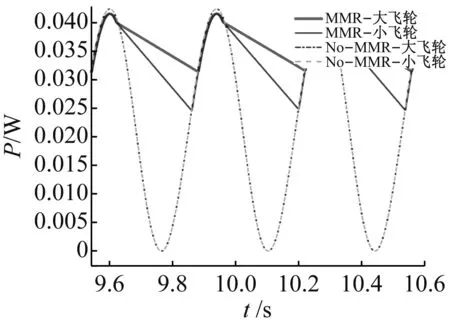
圖18 有/無飛輪和有大/小飛輪下功率曲線Fig.18 Relationship curve of power of TVIVEH vs. time with/without large/small moment of inertia

由圖18可知：

(1) 有單向離合器：轉動慣量較大的飛輪可以使得運動較為平緩；在脫離狀態下，大轉動慣量轉子系統的速度下降的速度要低于小轉動慣量轉子系統的速度下降的速度，說明大飛輪的轉子系統可以俘獲更多的可利用能量；在流體的輸入能量固定的情況下，該結構可以有效的提高裝置的俘能效率。與文獻[16]的研究結果對比，本文的仿真結果與文獻[16]有較大相似之處，也佐證了本文研究的正確性;

(2) 無單向齒輪結構：俘能裝置僅僅俘獲了上下運動中的一個方向的振動能量，無論是大小轉動慣量，都基本不會影響到裝置的俘能功率和俘能效率；飛輪的轉動質量的改變對于整個系統來說，影響很小，可以忽略不計。

3 結 論

本文將三穩態非線性系統和單向離合器結構引入渦激振動能量捕獲器中，提出了三穩態渦激振動電磁式俘能器，建立了力學模型及動力學方程，進行了數值仿真研究，主要結論如下：

(1) 與雙穩態系統相比，三穩態系統中勢阱深度較雙穩態淺，當兩種系統處于較弱的激勵時，三穩態系統產生大幅運動所需的外界能量低，可捕獲較多的流體動能。在整個流速過程中，三穩態系統的振幅比與發電功率也是高于雙穩態系統。

(2) 分別從質量比、鈍體直徑、負載電阻等因素探究了系統的最優參數；因單向離合器結構的存在，當發電機轉速下降到一定的數值時，鈍體上升運動會發電機輸入軸再次進入結合狀態，實現往返方向都能俘獲能量的目的，從而大大提升效率。