基于均值散布負熵信息圖的單向閥早期故障診斷方法
馮澤仲, 熊 新, 王曉東
(1.昆明理工大學 信息工程與自動化學院,昆明 650500;2.云南省礦物管道輸送工程技術研究中心,昆明 650500;3.昆明理工大學 云南省人工智能重點實驗室,昆明 650500)
礦漿管道是一種新型物料運輸方式,有效解決了礦源地偏遠,礦漿輸送困難的問題,具有節能、環保、廉價等優點。作為礦漿管道輸送的核心動力設備,隔膜泵能夠在高壓、高溫及高腐蝕等工況下較好的輸送漿體介質。其中,由于單向閥受較高的工作頻率及惡劣運行環境的影響,致使其成為隔膜泵中最易發生故障的部件,因此,開展單向閥故障診斷技術的研究對保障整個管道系統的安全可靠運行,避免重大事故的發生具有非常重要的意義[1]。
當由往復式部件組成的系統出現故障時會改變信號中的循環平穩特性[2],因而,學者們開發出了多種循環平穩指標用于表征往復式設備在不同健康狀況下運行時的特征[3]。從信號處理的角度來分析,通過及時的揭示能夠反映單向閥徹底失效時對應的特定頻率周期瞬變信息即可實現對故障的早期診斷[4-5]。然而,故障產生的初期其特征一般比較微弱,且常常受到復雜多變振動傳輸路徑的影響以及背景噪聲環境的干擾,使得能反映故障信息的沖擊性成分被淹沒于混合信號當中,這導致常規的信號處理方法難以有效地檢測出早期故障的微弱沖擊成分。
共振解調技術通過將信號中的特定頻率分量與無關干擾信息進行分離,為分析低信噪比信號中隱藏的周期性瞬態成分提供了一種有效的途徑。其中,快速譜峭度(fast kurtogram, FK)是一種經典的共振解調方法[6],它通過計算信號在不同頻段中的脈沖特性,可在二維頻譜圖中顯示敏感頻段所在的位置。然而,FK在處理信號中包含有非高斯噪聲(例如偶發脈沖)時會受到較大的干擾,這通常表現為非高斯噪聲將獲得比周期脈沖信號更高的峭度值[7]。為了克服這一缺點,Wang等[8]提出了雙樹復合小波包變換子頻帶均值峭度圖的方法,該方法采用的雙樹復合小波包變換可以有效細分高、低頻帶的同時還具有理想的平移不變形,通過子頻帶均值計算的方式有效緩解了非高斯噪聲對檢測周期性脈沖信號的影響。
另一方面,限制FK性能的一個重要因素是其無法識別信號中的循環平穩信息。為了提升對敏感頻段選取的有效性,Antoni引入負熵這一概念來等價峭度指標,創造性地使時域中的脈沖特性和頻域中的循環平穩特性共享了相同的物理意義,提出信息圖[9]的方法,這在很大程度上提升了診斷的有效性。然而,由于信息圖所采用的傳統Shannon熵對高斯噪聲較為敏感,容易導致高值出現在多個頻帶中,使得檢測結果變得難以解釋[10]。因此,為了提升信息圖在強非線性、非平穩的工程數據中的診斷能力,需為其提供更加魯棒的信號不規則衡量指標。近些年,一些非線性分析方法廣泛應用于機械設備故障診斷當中,如分形維數、排列熵[11]、近似熵[12]等。特別是排列熵和近似熵在機械設備裂紋檢測,故障診斷和剩余壽命預測等研究中表現出了不俗的性能。但這兩種方法也存在一些缺陷,例如:近似熵在檢測檢測較短信號時其性能不夠可靠,而在檢測較長信號時其速度較慢;排列熵相比于近似熵雖然在速度上有了較大的提升,但是排列熵對幅值的影響卻未有考慮,無法解決嵌入向量中出現的幅值相等情況。為了克服這些問題,Rostaghi等[13]提出了一種新的時間序列不規則衡量指標——散布熵。相比于其他方法,散布熵具有速度快、抗噪能力強、檢測結果可靠等優點。
綜上所述,本文針對原始信息圖在強背景噪聲和異常干擾環境下對單向閥早期故障的特征難以提取的問題,提出了一種基于均值散布負熵的單向閥早期故障診斷方法,即:分別通過散布熵和均值計算方法來緩解噪聲和異常干擾對診斷結果的影響。仿真和試驗分析結果均驗證了所提方法的有效性。
1 信息圖
1.1 平方包絡負熵(脈沖特性)
信號中的瞬態能量變化通常可用于描述系統由于異常沖擊等產生的脈沖激勵響應,因此,通過分析信號中瞬態的變化可以檢測信號中隱藏的周期性脈沖信息,其基本策略是通過一些標量指標(如波峰因子、峰峰值、峭度等)來量化沖擊的強度。而基于包絡信號強大的信息解析能力,通常在分析之前會先將原始加速度信號進行包絡變換[14]。對于濾波后的信號,通過希爾伯特變換,計算出解析信號的平方絕對值即可得到平方包絡(square envelope, SE)信號
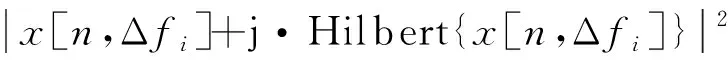
(1)
式中:SEx[n,Δfi]是長度為n帶寬為Δfi的信號;j是虛數單位。Antoni等通過分析指出,從本質上講,脈沖特性是非平穩性的一種表現形式,可通過一些用于分析非高斯信號的工具進行有效檢測。受到熱力學概念的啟發,將信號中的瞬態視為偏離了目標系統的平衡狀態,利用熵的概念來等效于峭度,并將其應用于SE中來檢測不同頻帶的非高斯信息,值得注意的是,譜熵與FK表現出了相反的行為,為了與FK保持一致的單調性,定義了譜負熵的概念
(2)
式中,〈·〉表示在信號的整個長度上執行平均運算。
1.2 平方包絡譜負熵(循環平穩特性)
除了檢測信號中的脈沖特性,頻譜相關性(spectral correlation, SC)是另一種檢測隨機信號中重復瞬變的有效工具。它被定義為協方差函數的雙重傅里葉變換,不但可以描述循環信息在頻譜頻率上傳播的固定載波的特性,而且可以描述循環頻率中的周期性隱藏調制[15]。當應用于循環平穩信號時,可用于描述頻譜坐標軸上等距分布的循環頻率調制諧波iα0。為了能夠簡單高效的分析信號中包含的循環平穩性,Borghesani等通過頻譜頻率軸上SC的積分/求和,建立了SC、SE和平方包絡譜(square envelope spectrum, SES)之間的關系[16],即:
(3)
式中:δ是離散的狄拉克函數;SESx,i[Δfi]表示頻率為α時的傅里葉系數;Fs是采樣頻率。SES中的諧波可以看作是與沿著循環頻率α軸高波動能量流的相關瞬變。通過測試SES中是否存在諧波,可以很好地實現周期性的有效檢測。因此,可以按照與時域瞬變類似的方法來量化評價SES的諧波結構。即:根據Parseval定理,循環平穩特性可用SES上的負熵進行描述
(4)
1.3 信息圖
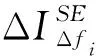
(5)
2 均值散布負熵
在本節,首先給出了散布負熵的計算方式;然后,對比分析了不同熵對噪聲的魯棒性;最后,引入一種均值熵計算方法以緩解偶發脈沖對診斷結果的誤導。
2.1 散布負熵
長度為N的信號x=x1,…,xN的散布負熵計算步驟如下:
(1) 利用正態分布函數將x映射到y={y1,y2,…,yN},y∈(0,1)中進行歸一化
(6)
式中,σ和μ分別表示標準差和期望。
(2) 通過線性變換將yj歸類到1至c個類中
(7)
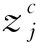
(3) 嵌入向量通過下式求得
i=1,2,…,N-(m-1)d
(8)
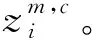
(9)
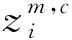
(5) 對于cm個可能的散布模式πv0…vm-1,其相對散布頻數計算如下
(10)
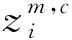
(6) 根據Shannon熵定義來求取x的DE。值得注意的是,對DE取負即為散布負熵(NDE)。
(11)
其中,根據經驗,時間延遲d通常設置為1,嵌入維數m=2~6,類別數c=3~10[17]。
2.2 噪聲對熵值的影響分析
為了定量描述機械設備由于故障產生的周期性脈沖信號,使用仿真的周期性脈沖響應信號如下
(12)
其中位移常數y0=2.5,相對阻尼比ζ=0.3,固有頻率fn=900 Hz,t為采樣時刻,設置重復周期T=0.04 s,即故障特征頻率fc=25 Hz,采樣頻率fs=12 kHz,模擬數據長度N=4 096,生成周期性脈沖仿真信號如圖2所示。

圖2 周期性脈沖仿真信號Fig.2 Periodic impulse simulation signal
為了測試不同形式的熵對噪聲的敏感性,我們對周期性脈沖信號中加入了不同強度的噪聲進行測試
s(t)=x(t)+e(t)
(13)
式中,e(t)表示高斯白噪聲。通常,當信噪比降低時,所有負熵的值都會減小,而通過測試不同形式的熵在較高信噪比下的數值變化情況則可以很好的反映其對噪聲的敏感程度。本文選取傳統的Shannon熵、排列熵(m=5,d=1)、近似熵(m=2,r=0.2*標準差)和散布熵(m=2,c=6,d=1)在不同信噪比下進行對比分析,標準化后的測試結果如圖3所示。
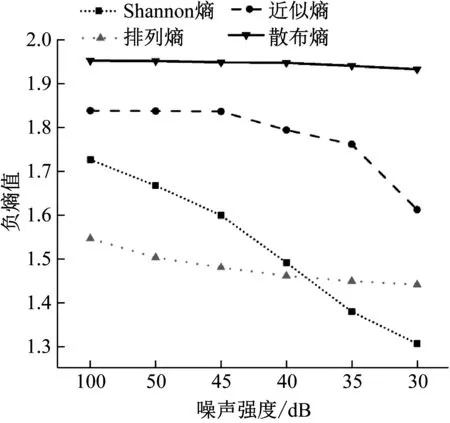
圖3 仿真信號在不同信噪比下的熵值變化情況Fig.3 Variation of entropy value of simulated signal at different SNR
從圖3可以觀察到,隨著信噪比在較高范圍內逐漸的降低,傳統Shannon熵值變化最明顯,對噪聲較為敏感;近似熵在噪聲強度在100~45 dB之間表現出了較好的穩定性,當小于45 dB后則變化較為明顯;排列熵和散布熵整體變化不大,而相比之下,散布熵最為穩定,對噪聲的魯棒性最強。
2.3 均值計算對熵值的影響分析
除了噪聲對信息圖的影響外,非高斯異常干擾也是限制信息圖診斷效果的另一個重要因素,例如在極端情況下,當瞬變信號過于密集以至于相互直接彼此重疊時,信號中的脈沖特性將會消失;而另一種極端情況是信號中由于異常沖擊干擾導致出現單一的脈沖時將得到最大的負熵值。因此,信號中的偶發脈沖在很大程度上阻礙了最佳頻段的選擇。為了緩解這個問題,本文提出了一種基于滑動窗的均值熵計算方法。
對于通過樹狀等分頻譜劃分方法得到的第i個子頻帶平方包絡信號SEx[n,Δfi],其滑動窗均值熵由下式計算可得
(14)
式中,M表示等分窗口的個數,本文設置M=4。為了分析提出的滑動窗均值熵在處理異常干擾和周期性脈沖信號時的有效性,在圖4中分別對比了原始的Shannon負熵和均值Shannon負熵的測試結果。
(a) 單脈沖負熵=3.684
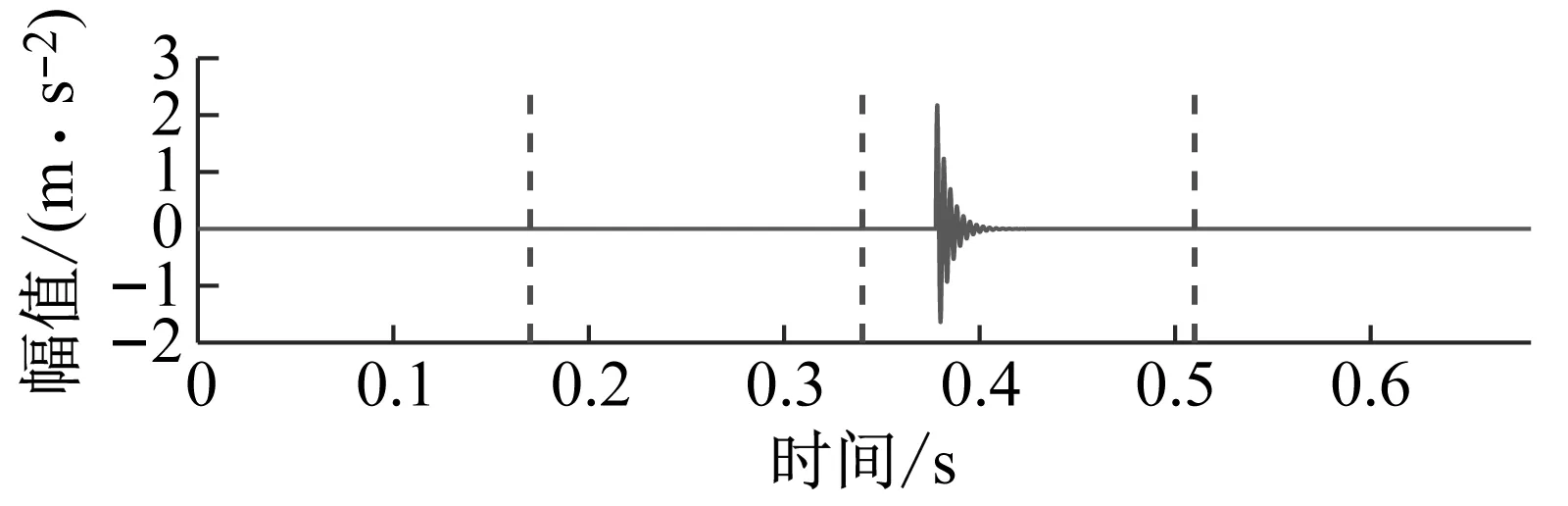
(b) 單脈沖均值負熵=0.834 75
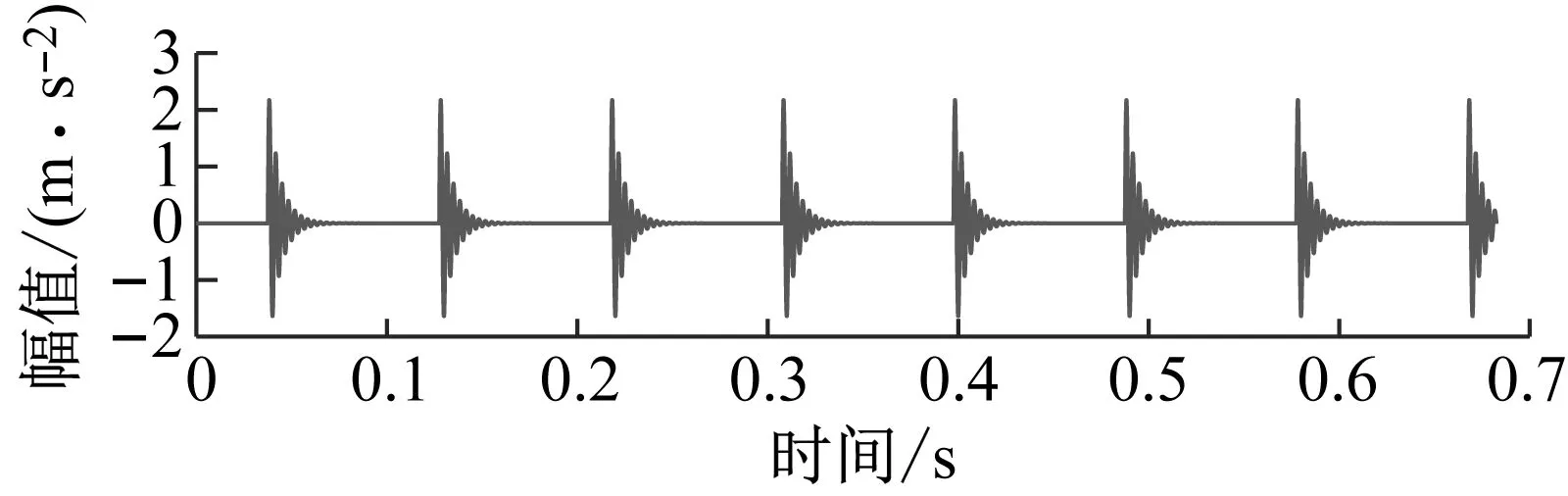
(c) 周期脈沖負熵=1.85
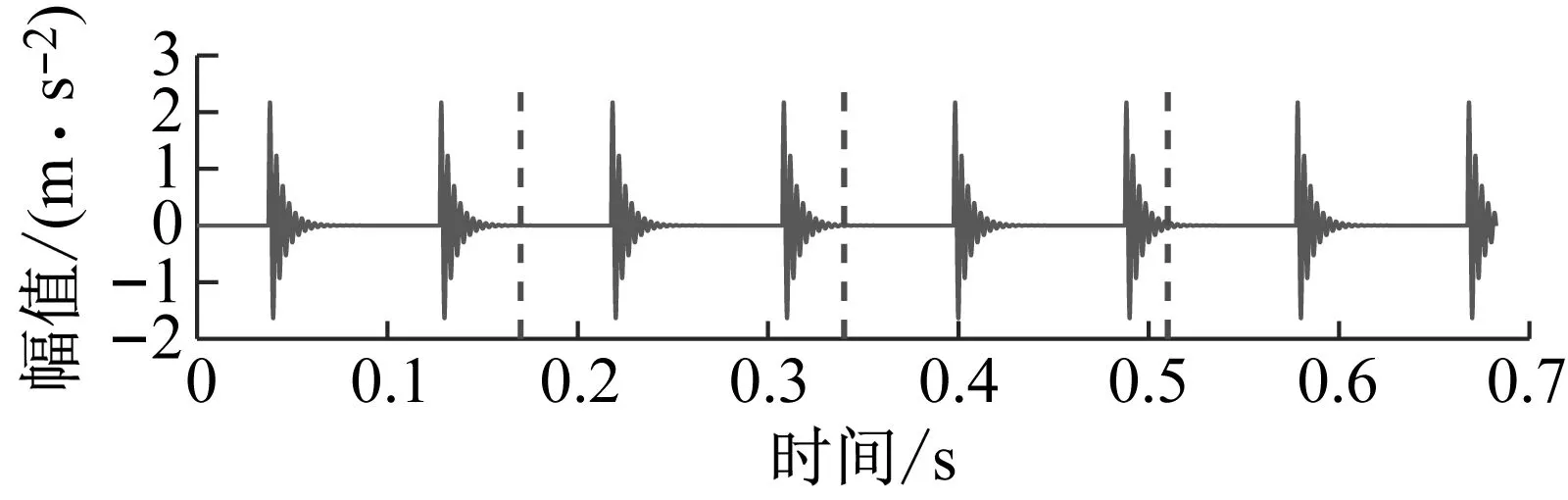
(d) 周期性脈沖均值負熵=1.834圖4 單脈沖、周期性脈沖信號分別對應的負熵和均值負熵Fig.4 Negentropy and mean negentropy corresponding to single impulse signal, periodic impulse signal respectively
從圖4可以看出,單脈沖信號的均值負熵遠小于原始信號的負熵;而對于周期性脈沖信號的均值負熵則和原始信號的負熵近似相等。這表明通過加窗均值操作可以顯著降低偶發異常干擾對時域中脈沖特性分析的影響。
3 基于均值散布負熵信息圖的單向閥早期故障診斷方法
本文利用均值散布負熵來改進信息圖,以更準確地提取機械故障時信號中存在的重復瞬變信息,實現對單向閥早期故障的診斷。所提方法的結構圖如圖5所示,具體步驟描述如下:
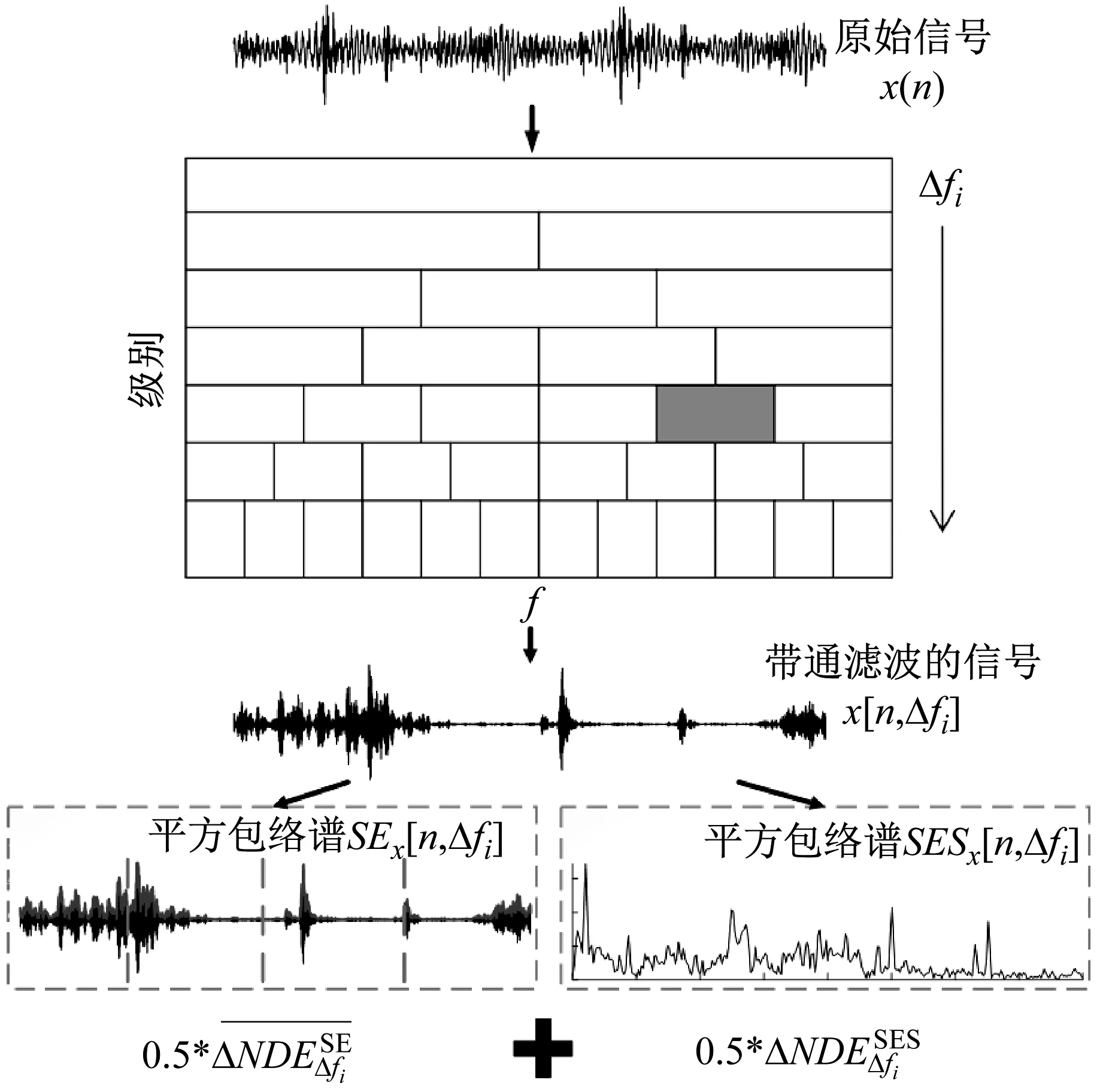
圖5 所提方法的結構圖Fig.5 Structural diagram of the proposed method
步驟1 對原始時間信號x(n),i=1,2,…,n采用樹狀濾波策略(如快速Kurtogram)分解為不同深度的子頻帶信號Δfi。
步驟2 根據式(1)和式(3)分別計算出每個子頻帶信號的平方包絡信號SEx[n,Δfi];以及平方包絡譜信號SESx[α,Δfi]。
步驟3 對于得到的SEx[n,Δfi]按照固定窗長進行M段等分,并求取該子頻帶信號的均值SE散布負熵
(15)
步驟4 對于得到的SESx[α,Δfi],求取該子頻帶信號的SES散布負熵
(16)
步驟5 通過對子頻帶的均值SE散布負熵和SES散布負熵進行加權平均求得平均散布負熵
(17)

4 仿真信號分析
為分析所提方法的有效性,在周期性脈沖信號(12)的基礎上,構建由偶發脈沖干擾i(t)、高斯白噪聲n(t)相互耦合的多分量信號。仿真信號表示為
s(t)=x(t)+i(t)+n(t)
(18)
其中周期性脈沖信號的位移常數y0=2.5,相對阻尼比ζ=0.09,固有頻率fn=900 Hz;重復周期T=0.03 s,采樣頻率fs=12 kHz,數據長度N=10 240,生成的周期性脈沖信號如圖6(a)所示;與偶發脈沖混合的信號如圖6(b)所示;對圖6(b)中添加SNR=-1 dB的高斯白噪聲,混合噪聲的信號如圖6(c)所示,可以看出由于較低的信噪比,原始周期性脈沖信號完全淹沒于噪聲中。為此,將所提方法用于提取隱藏于圖6(c)中的周期性脈沖信號。

(a)
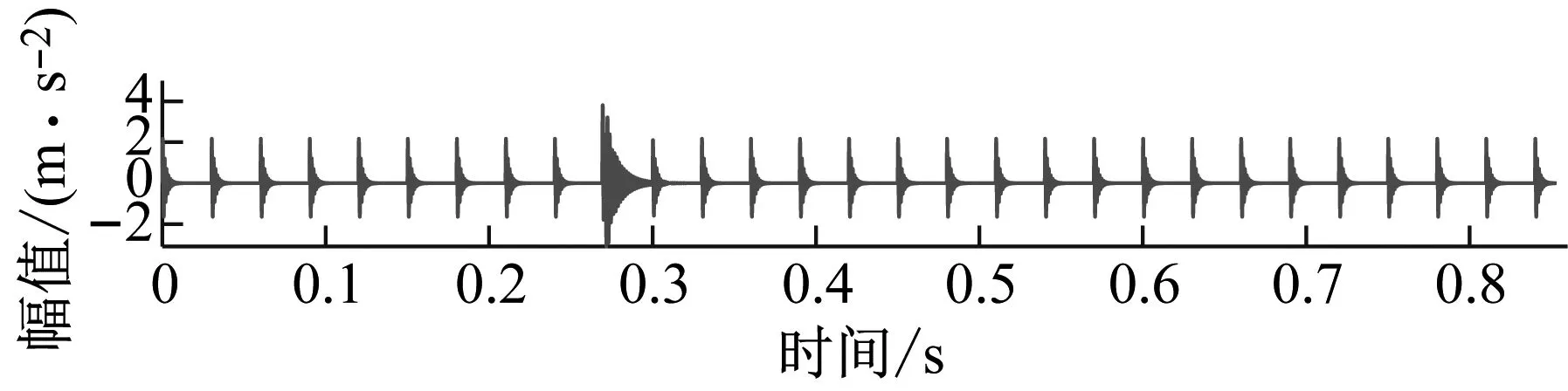
(b)
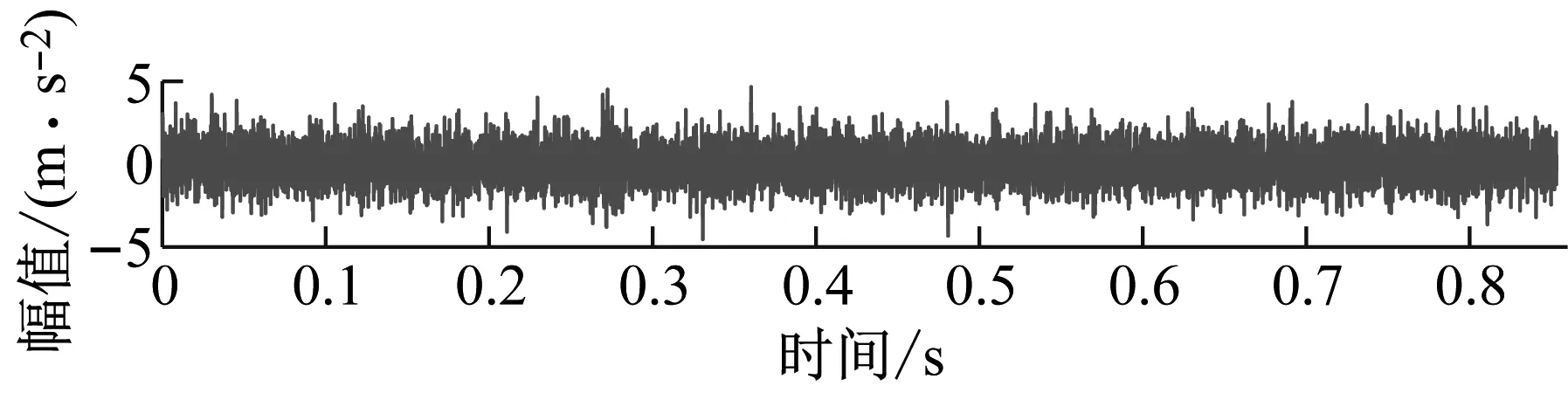
(c)圖6 周期性脈沖信號、加入偶發脈沖的混合信號及加噪信號Fig.6 Periodic impulse signals, mixed signals with occasional impulses, and noise-added signals
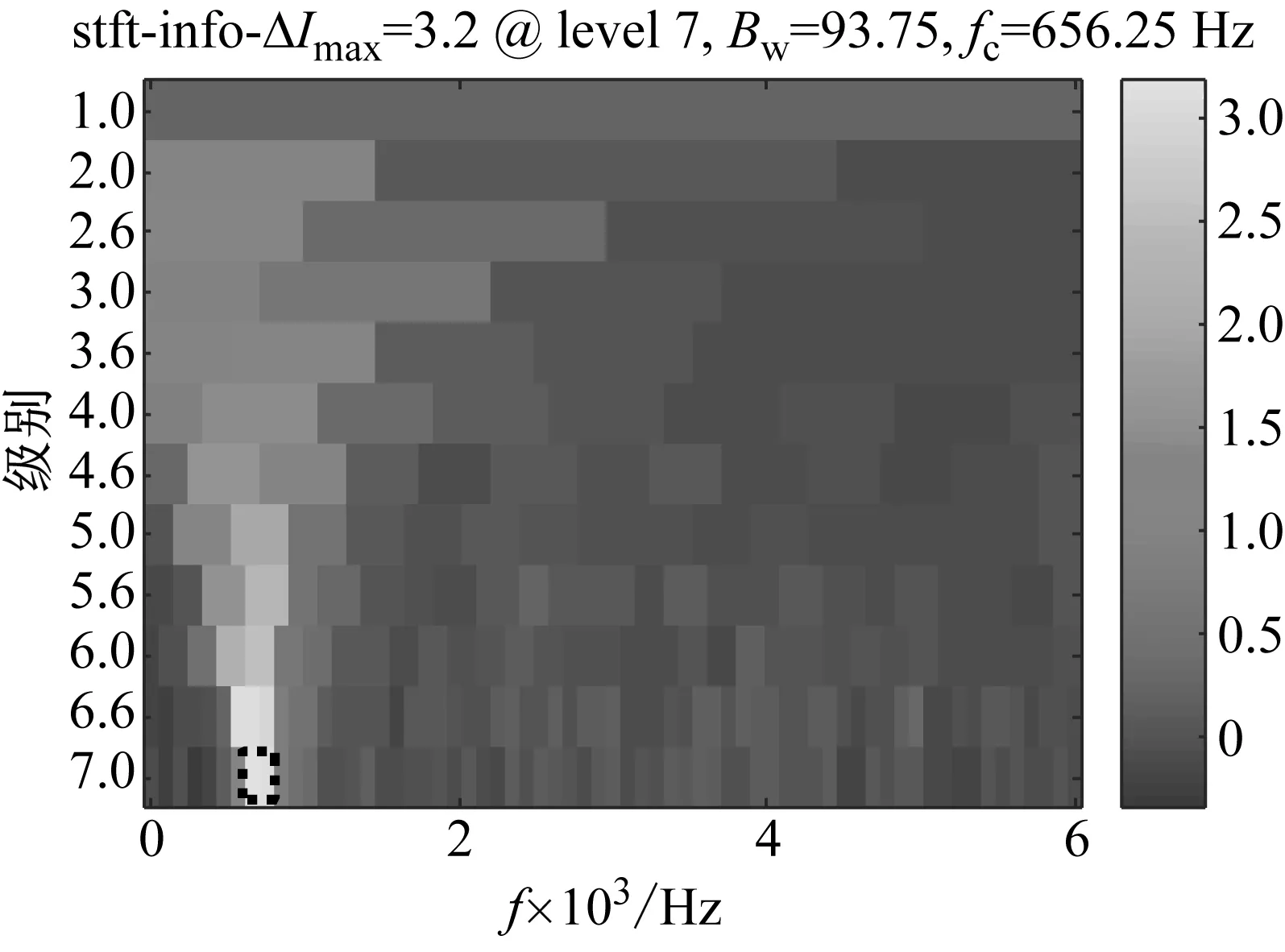
首先,通過均值散布負熵信息圖來確定濾波頻段的位置,其中熵值的不同大小對應不同的顏色。結果如圖7所示。
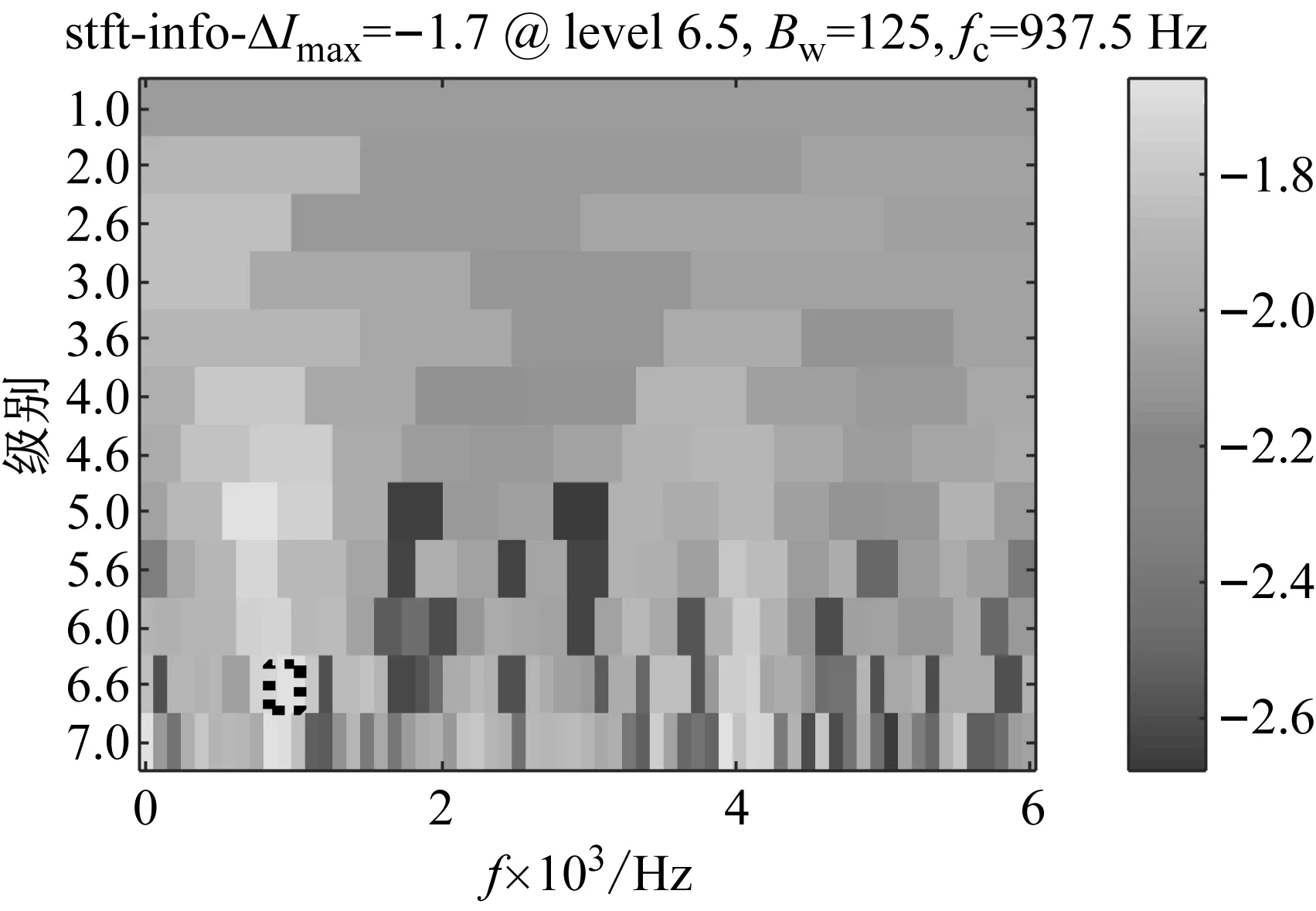
(a) 基于的信息圖
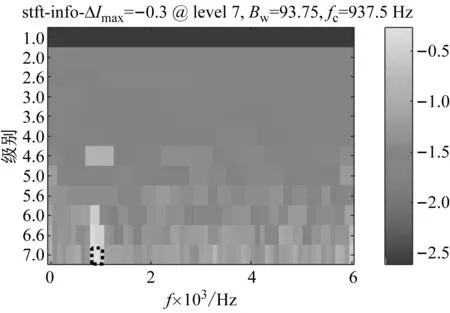
(b) 基于的信息圖
(c) 基于的信息圖圖7 仿真信號的均值散布負熵信息圖Fig.7 Mean dispersion negentropy infogram of the simulated signal
然后,利用選取的頻段對原始信號進行帶通濾波,濾波后的信號以及對應的平方包絡譜在圖8中示出。
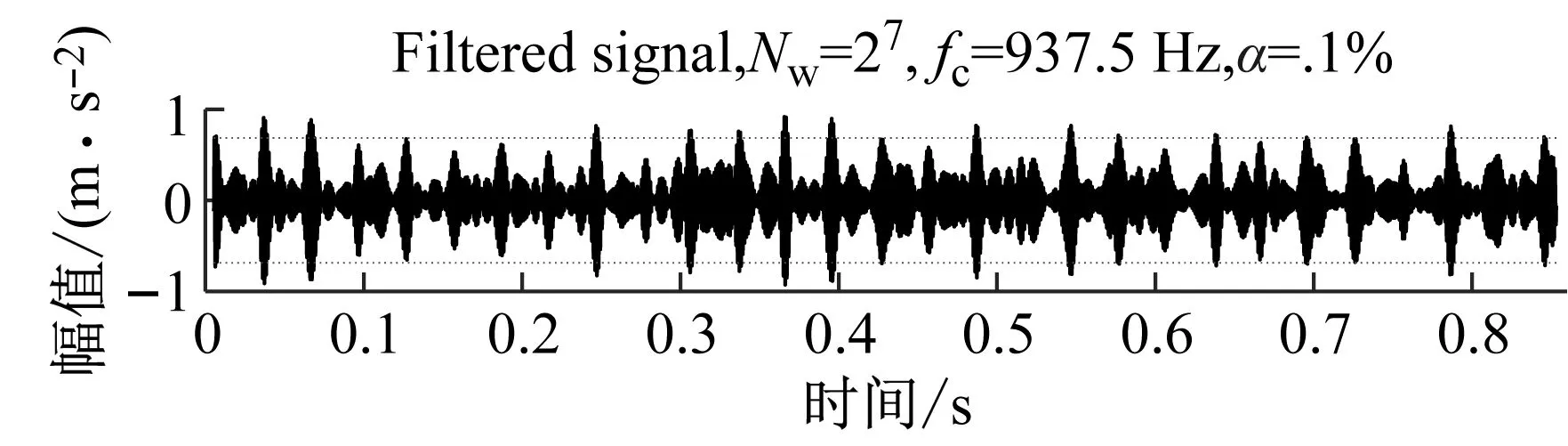
(a)
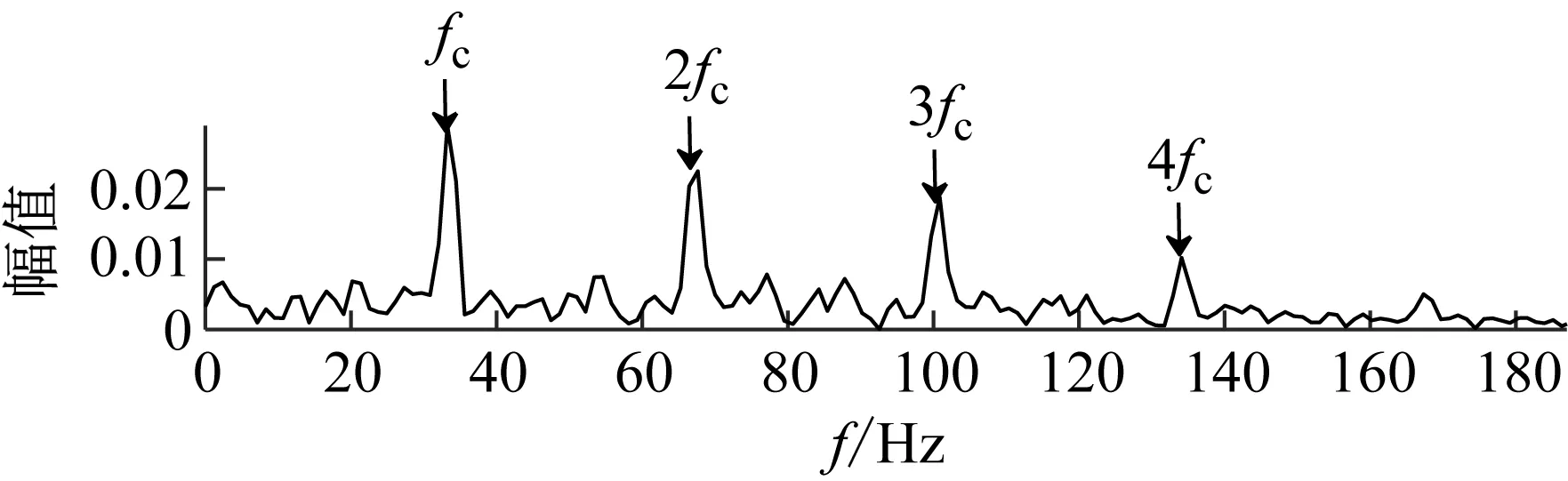
(b)圖8 基于信息圖所選頻帶過濾的信號及其SESFig.8 Frequency band filtered signal based on infogram and its SES
從圖8可以觀察到,濾波信號可以將大部分的噪聲濾除,對應的包絡譜不僅可以提取到故障頻率同時還提取到了多倍的諧波信息。
同時,為了進行比較,將原始的信息圖用于分析相同的信號中,分析結果如圖9所示。
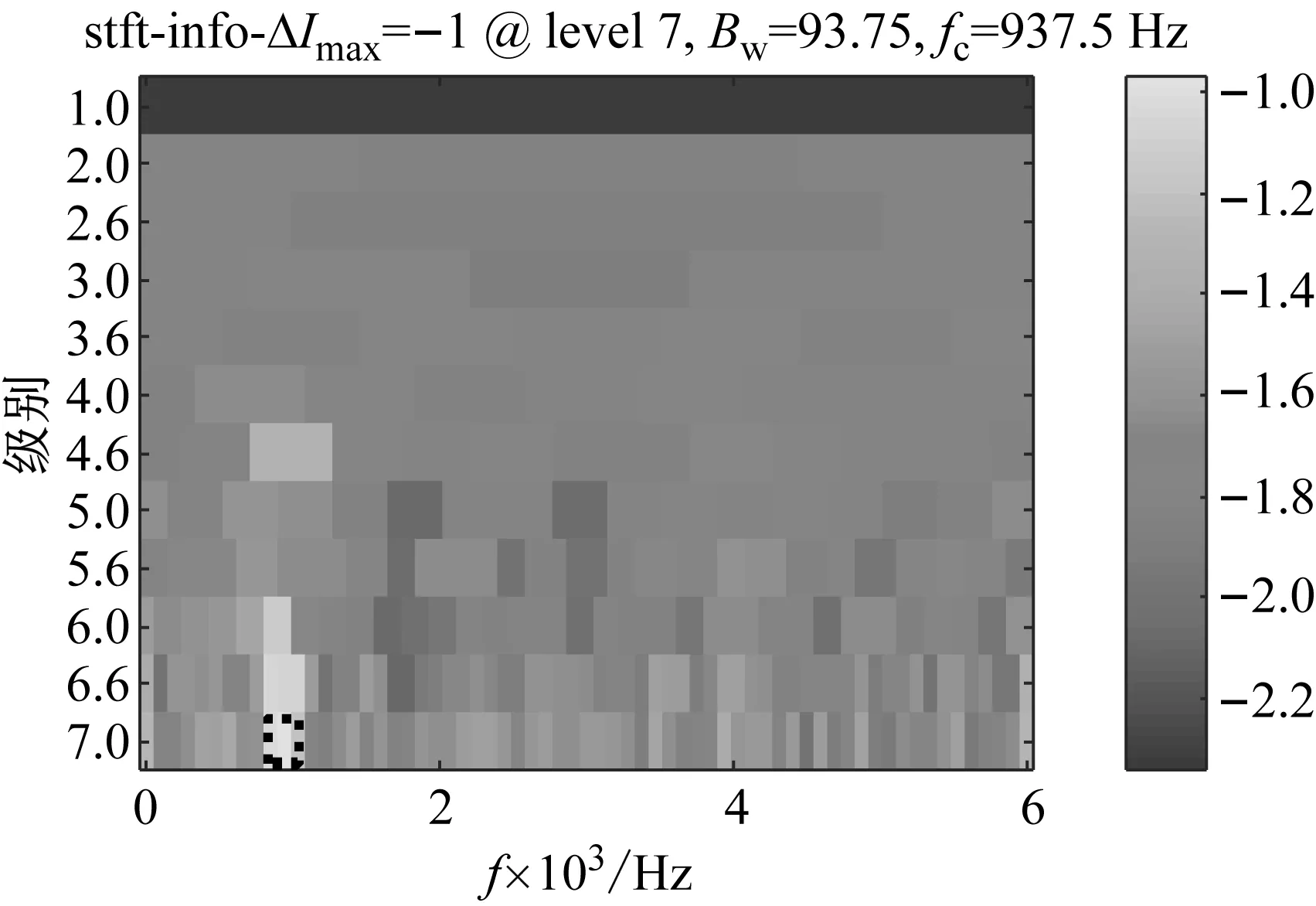
(a) 基于的信息圖
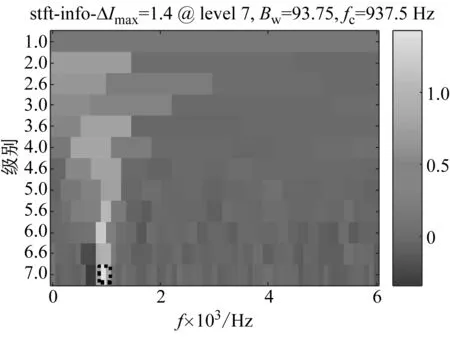
(b) 基于的信息圖

(c) 基于的信息圖圖9 仿真信號的原始信息圖Fig.9 Original infogram for simulation signals
(a)

(b)圖10 基于信息圖所選頻帶過濾的信號及其SESFig.10 Frequency band filtered signal based on infogram and its SES
5 試驗驗證
5.1 隔膜泵系統及故障單向閥
隔膜泵的動力由電動機經過齒輪箱傳遞給三拐曲軸和連桿,使得三拐曲軸的連續轉動變為十字滑頭的往復運動,從而帶動活塞在活塞缸內做往復運動,進而帶動隔膜做凹凸往復運動,使得隔膜室內的壓力發生變化,最終實現入料漿和排料漿的動作。隔膜泵系統及單向閥振動信號采集裝置如圖11所示。

圖11 隔膜泵系統及信號采集裝置Fig.11 Diaphragm pump system and signal acquisition device
表1為試驗采集信號所用器件及其型號,數據采樣頻率為2 560 Hz。
表1 數據采集器件和型號Tab.1 Data acquisition device and model
由于礦漿中固體顆粒的磨擦作用,泵組的進、出口單向閥工作一段時間之后勢必將產生磨損。一旦進、出口單向閥產生擊穿故障直至傷及閥室將產生重大經濟損失和安全隱患。因此,單向閥屬于隔膜泵狀態監測系統中重點監測對象。不同故障的單向閥如圖12所示。
圖13示出了高壓隔膜泵單向閥不同故障狀態的時域圖,分別是輸送介質持續沖擊閥門密封面產生凹坑并引起泄露的磨損故障信號(周期性瞬變信息被強背景噪聲淹沒);以及閥體擊穿故障(清晰的周期性脈沖信號)。
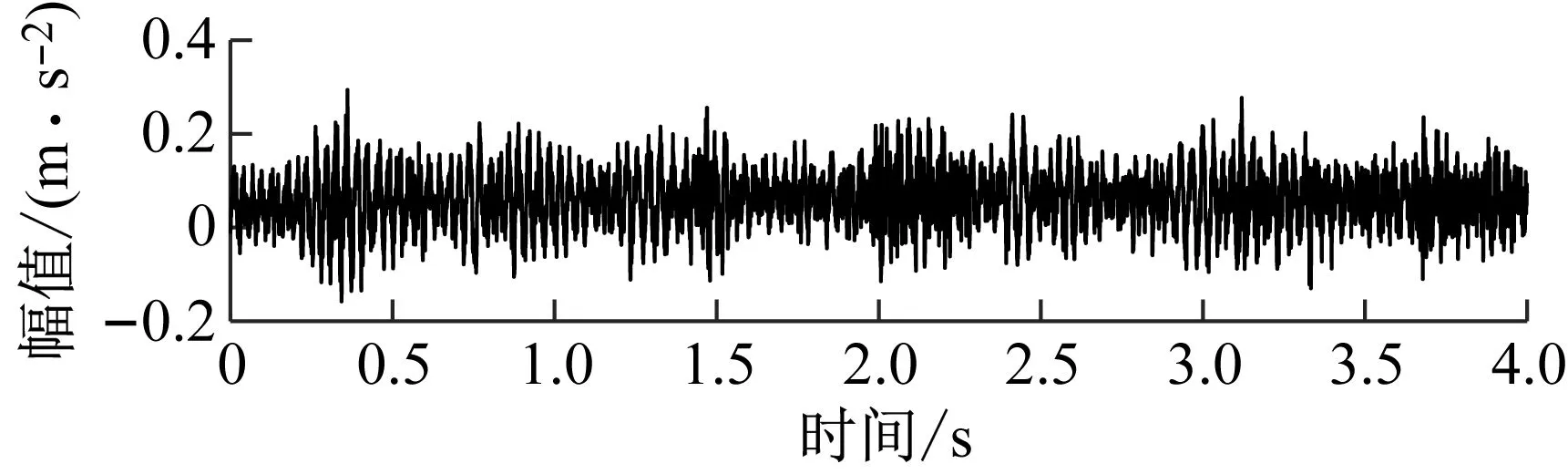
(a) 磨損故障信號
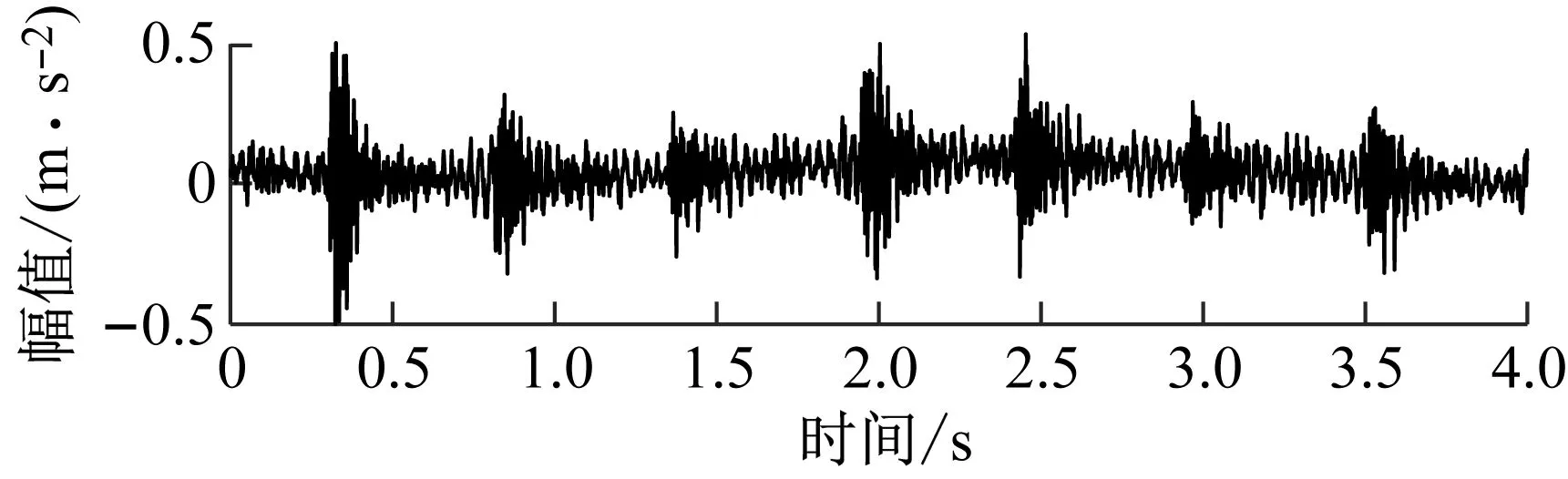
(b) 擊穿故障信號圖13 單向閥不同故障狀態的時域波形Fig.13 The time-domain waveforms for different failure state of the check valve
5.2 試驗結果與分析
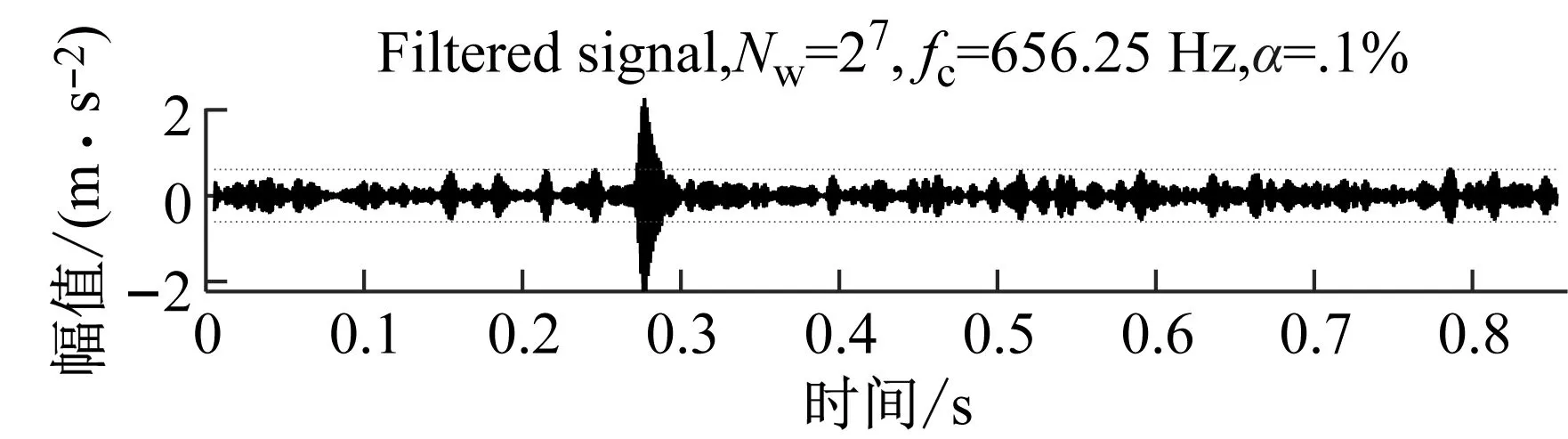
為了實現單向閥早期故障的診斷,將所提方法用于分析圖13(a)中的磨損故障信號,其中數據長度N=10 240。與仿真試驗一樣,首先,通過均值散布負熵信息圖來確定濾波頻段的位置,結果在圖14中示出。
從圖15可以觀察到,濾波信號表現出了與擊穿故障信號相同的周期性脈沖波形,對應的包絡譜也可以提取到擊穿故障頻率及多倍的諧波信息。
同時,為了進行比較,將原始的信息圖用于分析相同的信號中,分析結果如圖16所示。
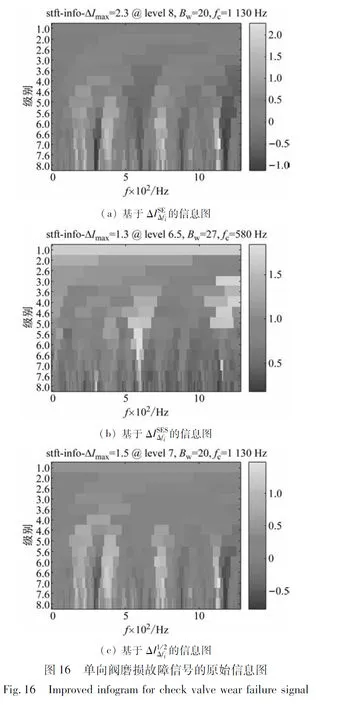
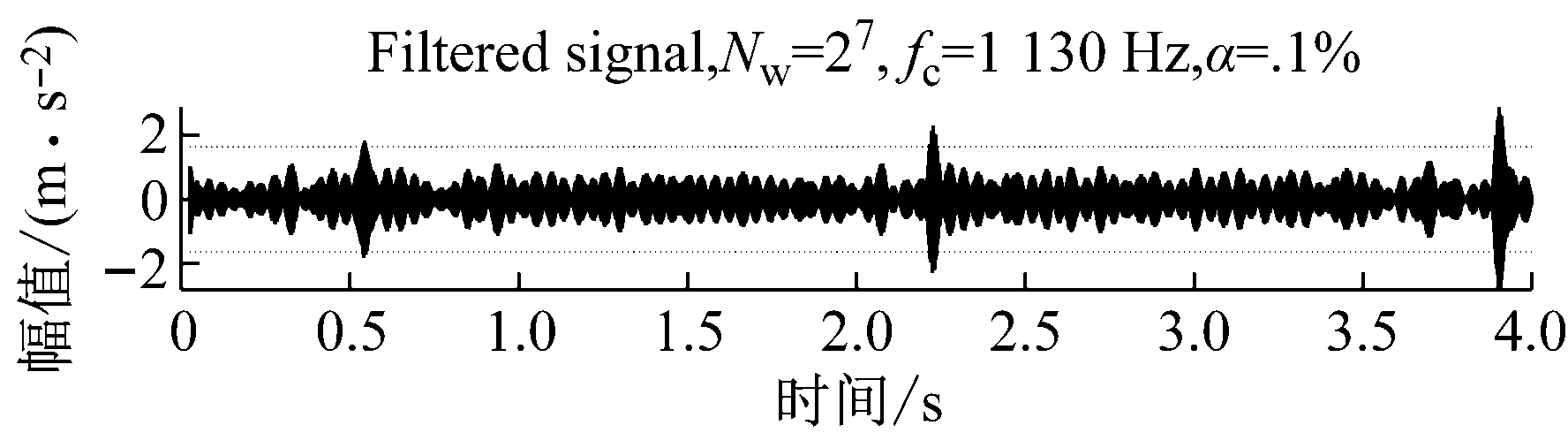
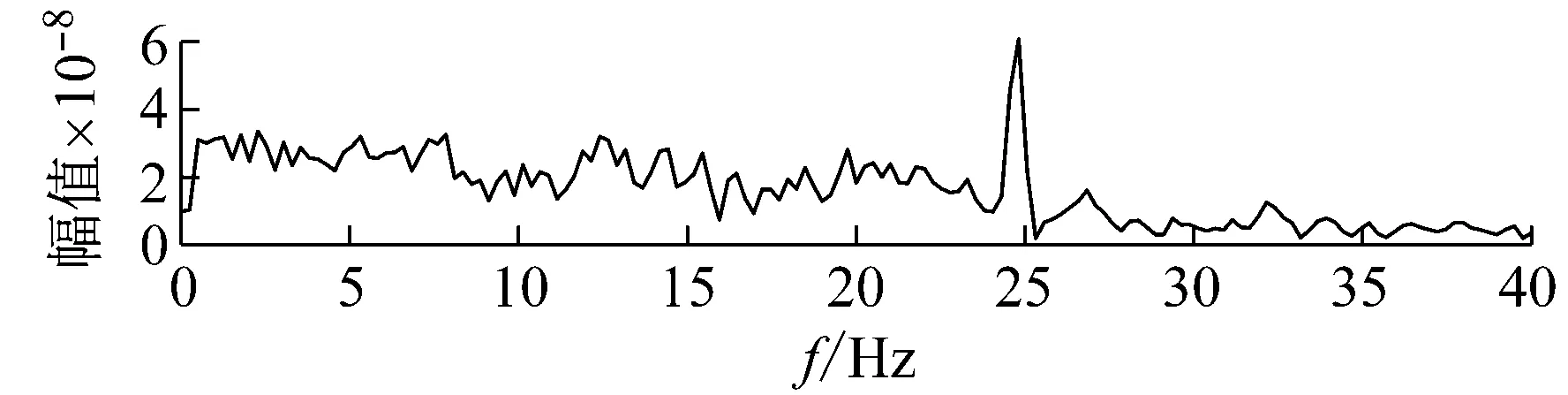
圖17 基于信息圖所選頻帶過濾的信號及其SESFig.17 Frequency band filtered signal based on infogram and its SES
綜上可知,仿真信號和工程數據均驗證了通過均值散布負熵改進的信息圖能夠從強背景噪聲以及混有異常干擾的信號中提取出重復瞬變信息,相較于原始的信息圖具有更強的魯棒性和有效性。
6 結 論
本文提出了一種隔膜泵單向閥故障診斷的新方法,分別在仿真信號和實測的單向閥故障信號中驗證了所提方法的有效性,并得出以下結論:
(1) 通過分析單向閥存在故障時的信號特性,將同時考慮了脈沖特性和循環平穩特性的診斷策略應用于早期故障診斷當中。
(2) 將子頻帶均值運算方法用于改善脈沖特性的檢測中,有效緩解了信號中存在異常隨機沖擊時對檢測結果的影響。
(3) 在原始信息圖的基礎上提出了基于散布熵改進的信息圖,相比于Shannon熵,散布熵具有一定的抗噪聲能力,可以更好地檢測單向閥振動信號中的動力學突變信息。

