曲線通過參數對高速列車牽引齒輪傳動系統動力學響應影響研究

尋麒儒， 魏 靜， 吳 昊， 李偉平

(重慶大學 機械與運載工程學院,重慶 400044)

高速列車技術近年來發展迅速，不僅對高速列車直線行駛的平穩性提出來了新的要求，而且對列車曲線行駛的平穩性提出了更高的要求，但列車行駛過程中由于復雜的路況，會出現超高與半徑不匹配的現象，這無疑會導致列車過彎時向心力不能完全平衡離心力，加上高速列車復雜的車軌耦合系統，使得高速列車的齒輪箱的動力學響應無法預測[1]。

近年來，國內外諸多學者對車輛曲線通過性能進行了大量研究[2-5]，但大多數的關注點在于列車輪對與輪軌間的相互作用力上。Wu等[6]通過建立詳細的貨車模型來研究曲線半徑、車速和軌道超高對彎道阻力的影響，得出了曲線半徑對彎道阻力影響最大，車速次之，超高影響最小；Yim等[7]以減小橫向氣隙為依據，評價了EMS型城市磁懸浮車輛的曲線通過性能，得出了磁懸浮列車曲線通過時，連接阻尼器的轉向架減小了橫向氣隙的變化，連接桿的轉向架增大了橫向氣隙的變化；Zhai等[8]研究了提速機車車輛通過不同曲線軌道時，輪軌動態橫向相互作用性能指標，得出了提速后列車通過曲線軌道時，輪軌橫向動態相互作用加劇，動力學性能指標的最大峰值均出現在圓曲線上。

針對車輛曲線通過時，車輛系統振動響應性能的研究，鮑凱曼等[9]分析了鐵路曲線線路的幾何特征，獲得了車線耦合系統在不同曲線參數，不同行車速度和不同軌道不平順下對車體響應的影響規律；魏慶朝，龍許友等[10]揭示了線路平縱橫斷面設計參數、平縱斷面組合及區段線路設計方案對車線系統動力響應的影響規律；宣言等[11]建立了較為全面的車線耦合系統有限元動力學仿真模型，對客運專線曲線線路的車線耦合系統進行了仿真分析，得到了列車橫向和垂向振幅與曲線半徑與超高值的關系；李揚等[12]以車組鏈輸送機為研究對象，利用SIMPACK建立軌道車組模型，從不同的工況條件和軌道小車的結構，得出了車組的動態性能隨著車距的減小而增大，且隨著曲線半徑和緩和曲線長度的提高而增大的結論；Kurzeck等[13]研究了輕軌車輛在通過不同曲線半徑時軸箱的振動加速度的變化，找出了車輛內部的產生振動和噪聲的原因。

總體來看，對車輛曲線通過能力的研究多集中于車輛車體的動力學響應以及車軌間的相互作用力等，對牽引齒輪傳動系統的動力學響應的研究還很匱乏。本文以復興號某型高速列車為研究模型，運用車輛多體動力學理論建立高速列車剛柔耦合動力學模型，包含完整的齒輪傳動部分，通過設置不同線路工況，仿真分析曲線半徑和超高值對高速列車牽引齒輪傳動系統動力學響應的影響，揭示其規律。

1 高速列車牽引齒輪傳動系統剛柔耦合動力學模型

高速列車牽引齒輪傳動系統剛柔耦合動力學模型如圖1所示，高速列車由一個車體、兩個轉向架、四個輪對組成，每組輪對上裝有一個電機和齒輪箱。車體、轉向架和電機視為剛性，輪對，齒輪箱和齒輪副視為柔性，且每個部件的質量和轉動慣量集中在質心，并且考慮了車體、轉向架等的六個自由度，即縱向(Xi)、橫向(Yi)、垂向(Zi)、側滾(φi)、點頭(θi)和搖頭(ψi)，這里的下標i=m、ws、b、c，p，g分別表示電機，輪對，轉向架，車體，小齒輪，大齒輪。每個轉向架與兩組輪對(Zw)通過彈簧(Kpz)-阻尼(Cpz)支承，車體與兩個轉向架通過二系懸掛(Ksz、Csz)支撐，電機通過螺栓固定在轉向架上，齒輪箱一端通過吊桿(Kbs、Cbs)懸掛在轉向架上，另一端通過軸承安裝在輪對上，整個列車由軌道子結構支撐，并通過輪軌力(Pi)接觸軌道運行，對于圖1中的軌道子結構模型，采用了一種典型的軌道結構，包括鋼軌、軌枕和路基，鋼軌被模擬成一個連續的伯努利-歐拉梁(EIY)，(Kpi、Cpi)和(Kfi、Cfi)分別表示鋼軌與軌枕和軌枕與地基間的彈簧和阻尼，i表示軌枕的個數，符號Msi表示軌枕的質量[14]，高速列車模型各部件自由度如表1所示。

表1 高速列車模型自由度Tab.1 High speed train model degree of freedom

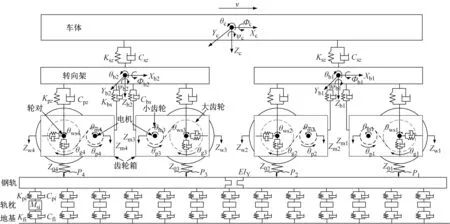
圖1 高速列車齒輪傳動系統剛柔耦合動力學模型Fig.1 Rigid-flexible coupling dynamics model of high-speed train gear transmission system

高速列車系統運動微分方程的矩陣形式為

(1)

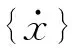
各部分垂向、點頭、縱向運動方程[15]如下

(1) 車體的運動方程

車體垂向運動：

(2)

車體點頭運動：

Fbr2(Hczcosαbr2-Hcxsinαbr2)-Fctx1Hcb-Fctx2Hcb

(3)

車體縱向運動：

(4)

(2) 前、后轉向架的運動方程

前轉向架垂向運動：

(5)

前轉向架點頭運動：

(6)

前轉向架縱向運動：

(7)

后轉向架垂向運動：

(8)

后轉向架點頭運動：

(9)

后轉向架縱向運動：

(10)

(3) 輪對的運動方程(i=1～4)

輪對垂向運動：

(11)

輪對縱向運動：

MwsXwsi=2Pui-Ftwxi+(-1)i+1|Fgi|cosβbi

(12)

輪對旋轉運動：

(13)

式中:Ftwi為一系懸掛垂向作用力;Ftwxi為一系懸掛縱向作用力(i=1～4);Fctn為二系懸掛垂向作用力;Fctxn為二系懸掛縱向作用力(n=1～2);Fbr1為前轉向架牽引拉力;Fbr2為后轉向架牽引拉力;αbri為牽引拉桿與x反方向間夾角;Ftmi為電機懸掛垂向作用力;Ftmxi為電機懸掛縱向作用力;Hcb為車體質心與二系懸掛的垂向距離;Hta為輪對質心與構架質心的垂向距離;Htb為二系懸掛與構架質心的垂向距離;Hcx、Hcz為牽引拉桿距車體質心的縱向距離和垂向距離;Htx、Htz為牽引拉桿距轉向架質心的縱向距離和垂向距離;Lc、Lt、L1分別為為車輛定距之半、轉向架軸距之半、電機箱體懸掛點到構架質心的縱向距離;hta為轉向架質心與電機懸掛構架質心的垂直距離;Pi、Pui為輪軌垂向力與切向力;Fcx為列車阻力;Fgi為齒輪副間嚙合力;R0為車輪半徑;Tgwi為大齒輪與輪對間的扭矩;βbi為斜齒輪螺旋角。

為了獲得準確的齒輪箱振動響應及齒輪嚙合特性，對牽引齒輪箱傳動系統進行詳細的建模，牽引齒輪箱傳動系統幾何模型如圖2(a)所示，圖2(a)中淺色圓點為柔性體主要縮聚點位置，大小齒輪副每個齒上各有一個縮聚點，電機輸出軸輸出牽引力矩Tm，通過聯軸器將牽引力矩傳遞至齒輪箱小齒輪端，小齒輪與大齒輪通過齒輪嚙合將扭矩傳遞至列車輪對，驅動輪對轉動為列車提供驅動力[16-17]。本文采用有限元法和自由度縮減理論，將傳動系統中的齒輪箱箱體及大小齒輪均處理為柔性體，由于齒輪嚙合傳動時齒面為接觸面，接觸應力較大，彈性變形也較大，故齒輪縮減自由度的主節點主要設置在齒上，因此齒輪箱及大小齒輪在受載情況下均可以發生彈性變形和振動[18]。

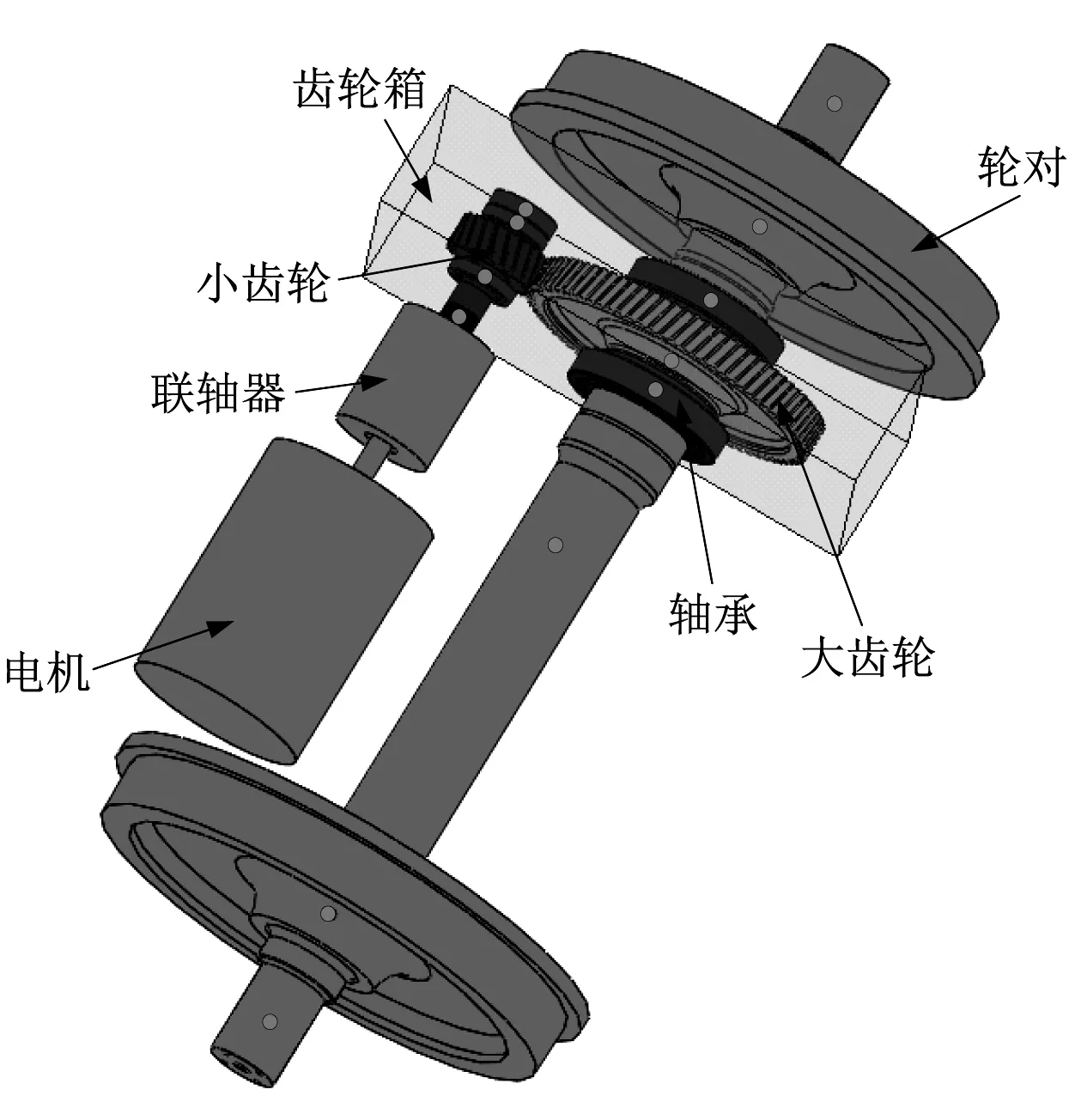
(a) 幾何模型

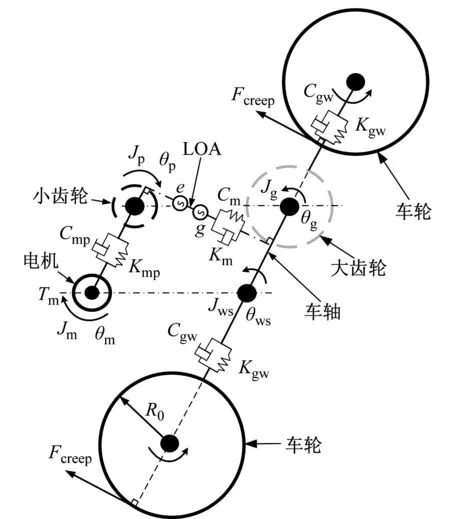
(b) 動力學模型圖2 高速列車牽引齒輪傳動系統模型Fig.2 Traction gear transmission system model of high-speed train

高速列車齒輪傳動系統斜齒輪在嚙合過程中，齒輪嚙合力的軸向分量會導致系統產生扭轉振動和x、y、z三個方向的振動，為了保證高速列車齒輪轉動系統建模的精密性，綜合考慮齒輪時變嚙合剛度、嚙合阻尼、嚙合誤差和齒側間隙，在不考慮輪對打滑的情況下，建立如圖2(b)所示的高速列車牽引齒輪傳動系統動力學模型，定義系統廣義位移矩陣為[19]

{δ}={θm,xp,yp,zp,θp,xg,yg,zg,θg,θws}T

(14)

主動輪順時針轉動時的嚙合線位移為：

δpg=cosβbsinαpgxp-cosβbcosαpgyp+

sinβbzp-rpcosβbθp-cosβbsinαpgxg+

cosβbcosαpgyp-sinβbzg-rgcosβbθg-e-g

(15)

建立高速列車牽引齒輪傳動系統動力學方程為

(16)

Kmδpg)=0

Kmδpg)=0

Kmδpg)=0

(17)

(18)

Kmδpg)=0

Kmδpg)=0

Kmδpg)=0

(19)

(20)

-2FcreepR0

(21)

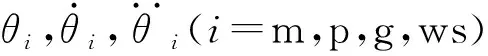
為了準確評估曲線參數對高速列車齒輪箱傳動系統動態影響，本文運用有限元法通過ANSYS軟件對齒輪箱箱體、齒輪副及輪對進行縮聚，其中齒輪副參數如表2所示。高速列車傳動系統主要動力學參數如表3所示。

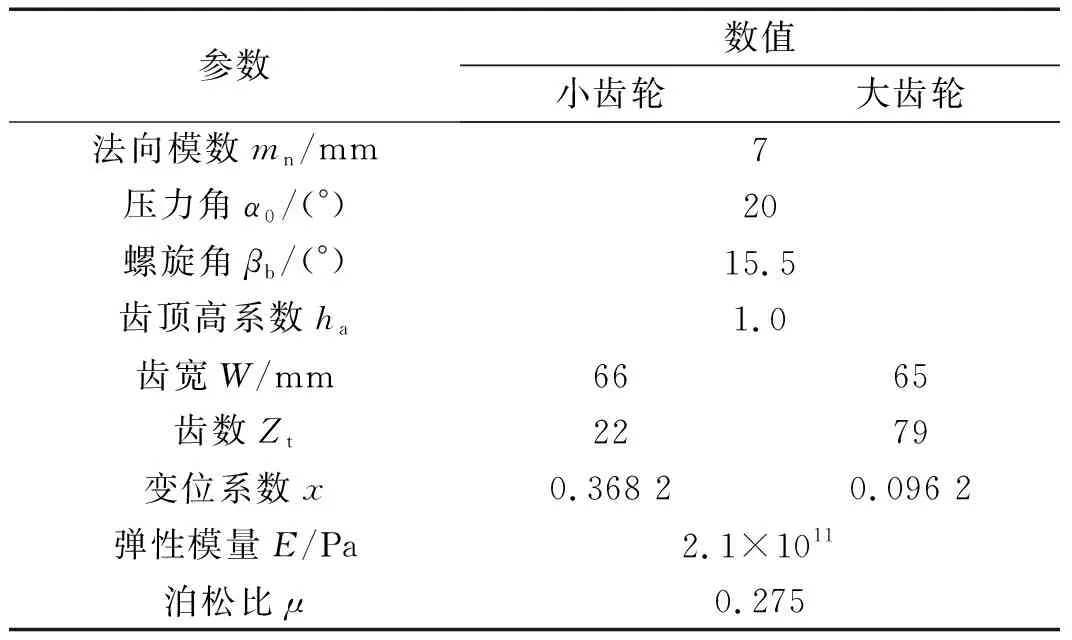
表2 齒輪副參數Tab.2 Gear pair parameter

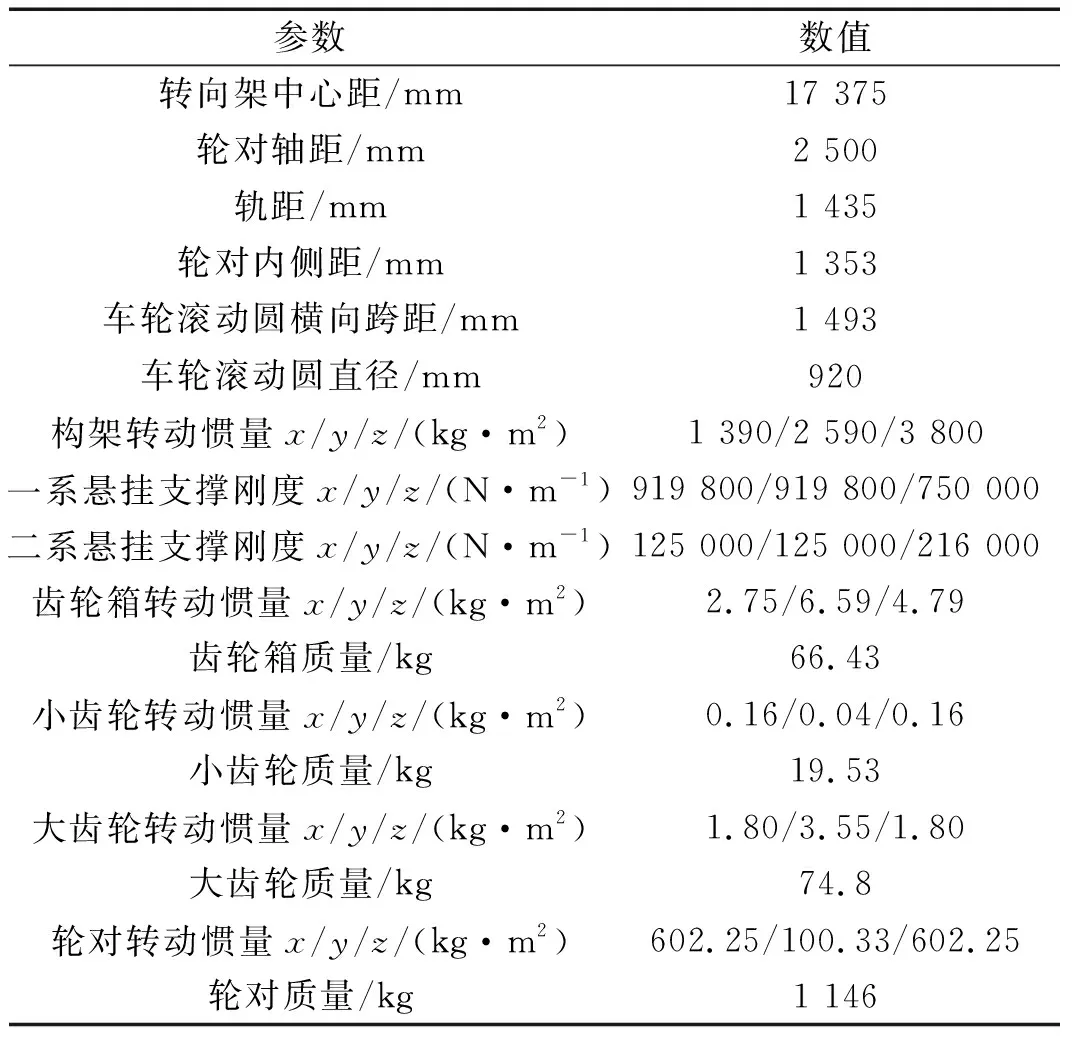
表3 高速列車傳動系統主要動力學參數Tab.3 Main dynamic parameters of high speed train system

將高速列車牽引傳動系統各部件抽象為剛體或柔性體，各部件相互連接，相互制約，構成彼此互相約束的剛柔耦合多體動力學系統，剛體部件選取其質心在慣性參考系中的笛卡爾坐標和反應剛體方位的歐拉角等6個廣義坐標描述；柔性體部件除選取笛卡爾坐標和歐拉角還需選取模態坐標共7個廣義坐標描述，其中模態坐標采用固定界面模態綜合法縮聚為有限自由度，先將運動進行分解，并通過拉格朗日方程可推到出高速列車剛柔耦合系統運動控制微分方程見式(22)[20-21]

(22)

式中:[M]為高速列車構件質量矩陣;{ξ}為高速列車構件廣義坐標列向量;[K]為高速列車構件廣義剛度矩陣;[D]為對稱的常數阻尼矩陣;{fg}為重力引起的廣義力列向量;C(ξ,t)為約束方程;λ為拉格朗日乘子;{Q}為廣義力矩陣。

柔性體模型采用ANSYS和SIMPACK軟件通過FEMBS來生成，用ANSYS軟件生成彈性子結構，用SIMPACK建立剛柔耦合模型，具體流程如圖3所示。

圖3 剛柔耦合模型流程圖Fig.3 Flow chart of rigid-flexible coupling model

根據剛柔耦合模型流程圖搭建的高速列車齒輪箱傳動系統剛柔耦合模型如圖4所示。

圖4 高速列車齒輪箱傳動系統剛柔耦合模型Fig.4 Rigid-flexible coupling model of high-speed train gearbox transmission system

2 曲線參數及測點位置

2.1 曲線參數

圖5示為列車曲線通過時的受力狀態，當列車曲線通過時，會產生一定的離心加速度aL，使列車的輪對緊靠外側軌道運行，增加了外部軌道的壓力，為了抵消離心力的作用，通常將曲線路段外軌道適當抬高，列車的重力產生一個向心的水平分力aX，使內外軌受力均勻，從而提高列車曲線通過時的穩定性和安全性。外軌抬高后產生的外軌頂面與內軌頂面的水平高度之差稱為曲線超高h[22]。

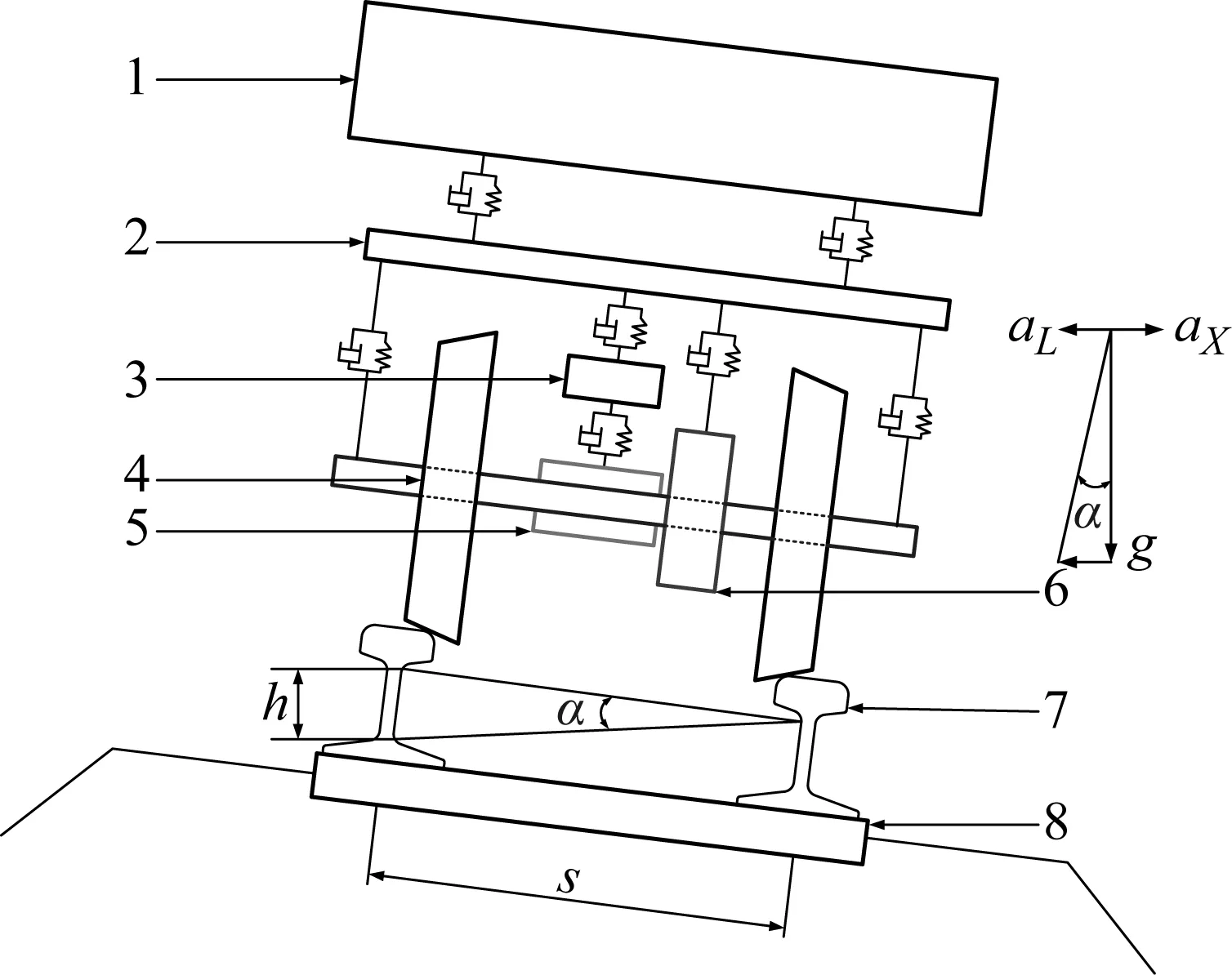
1.車體;2.構架;3.電機吊架;4.輪對;5.電機;6.齒輪箱;7.鋼軌;8.軌枕。圖5 列車曲線通過時所受離心力和向心力Fig.5 Centrifugal and centripetal forces of train passing curve

將不同的曲線參數(曲線半徑R、曲線超高h)進行組合，對已經建立的剛柔耦合列車模型進行了試算分析，來研究曲線參數對高速列車齒輪傳動系統動態響應的影響。為了更好地揭示不同的曲線參數對高速列車傳動系統振動響應及齒輪嚙合性能的影響，所涉及的計算結果均未考慮軌道隨機不平順。在選定列車曲線通過工況時，僅考慮R和h滿足規范的要求，對未被平衡的超高不再加以限制[23]，以此保證統計數據的連續性。

設定的運行線路由5個部分組成，分別是直線段，圓曲線段，緩和曲線段，圓曲線段，直線段，計算時選用高速鐵路緩和曲線型式三處拋物線，超高形式為外軌超高。由于三次拋物線為直線型順坡變化的緩和曲線，在緩圓點處存在曲率和超高的一階、二階、三階導數的不連續變化，從而引起車輛運行性能的局部突變，而在圓曲線段近似為一段水平的直線段。根據文獻[24]，此次共設置共8種超高值(40～180 mm)，4種半徑值(5 500 m，7 000 m，8 000 m，9 000 m)進行組合，列車行駛速度為250 km/h，曲線參數如表4所示。

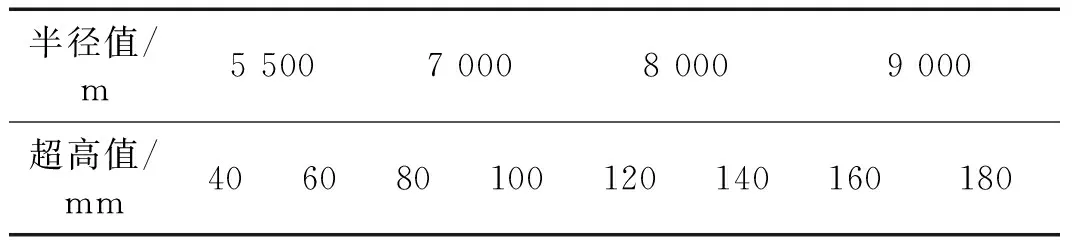
表4 曲線參數組合Tab.4 Curve parameters

2.2 齒輪箱測點位置

為準確測量齒輪箱軸承等處振動加速度大小，采用自由度縮聚方法對柔性牽引齒輪箱箱體進行縮聚，并在縮聚點處設置傳感器，具體測點位置如圖6所示。

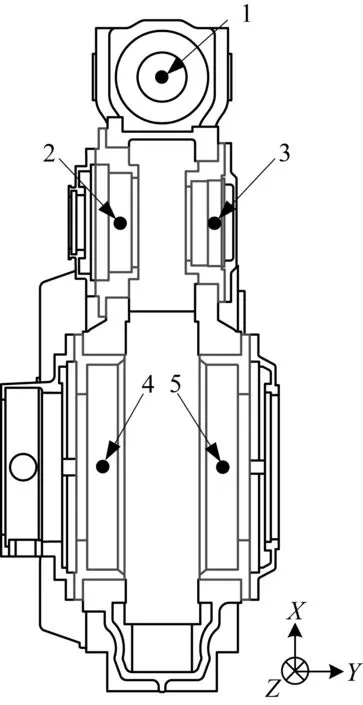
1.齒輪箱吊桿支座;2.圓柱滾子軸承;3.四點球軸承;4.左側圓錐滾子軸承;5.右側圓錐滾子軸承。圖6 齒輪箱傳感器位置Fig.6 Gearbox sensor position

3 齒輪傳動系統動力學響應分析

3.1 超高影響率及超高因子

如圖7所示為齒輪箱測點3在不同曲線通過參數下x向振動加速度RMS值。從圖中可以看出，在超高值40 mm下，不同的半徑對應齒輪箱測點振動加速度RMS值差異很大，但在超高值160 mm下，不同的半徑對應齒輪箱測點的振動加速度RMS值則很小，為了便于分析，本文將超高對不同半徑對振動加速度RMS差異的影響稱作超高影響，影響程度的大小用超高影響率來表示，從圖7中可以看出，齒輪箱測點的振動加速度隨著半徑值的遞增呈現線性變化，故本文的超高影響率用半徑5 500 m和9 000 m對應的振動加速度RMS值的差異率μ來表示，見式(23)

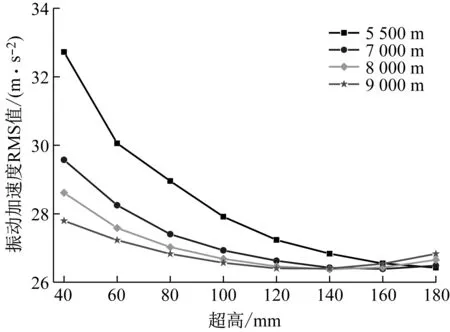
圖7 齒輪箱測點3處x向振動加速度Fig.7 x-direction vibration acceleration at measuring point 3 of the gearbox

(23)

式中,ai，aj表示齒輪箱振動加速度幅值大小，將出現超高影響率極大值或者極小值對應的超高值稱作超高因子。

3.2 齒輪箱振動加速度

振動加速度幅值的大小可以反應出列車曲線通過時齒輪箱動力學響應的劇烈程度。如圖8所示為齒輪箱測點1(吊桿支座)在不同曲線參數下計算的振動加速度RMS值及超高影響率曲線圖。

圖8 齒輪箱測點1(吊桿支座處)Fig.8 Measuring point 1 of the gearbox(suspender)

從圖8中可以看出，齒輪箱測點1處x向振動加速度RMS值隨著超高的增大呈現先減后增的趨勢，存在一個拐點，而且曲線半徑越小，拐點對應的超高越大，如圖8所示，半徑5 500 m拐點對應超高為100 mm，半徑7 000 m拐點對應超高為80 mm，半徑8 000 m拐點對應超高為60 mm，而半徑9 000 m則無拐點；y向振動加速度隨著超高和曲線半徑的增大而增大；z向振動加速度隨超高的增大呈現先減后增的趨勢，也存在明顯的拐點，如半徑5 500 m無明顯拐點，其余三組半徑(7 000 m、8 000 m、9 000 m)，拐點對應的超高均為140 mm。

從圖8中所示的齒輪箱測點1處x，y，z方向上超高影響率變化曲線圖，可以看出x向超高影響率隨著超高的增大呈現先下降后上升最后趨于平緩的趨勢，且在超高值40 mm有極大值，超高值為60 mm有極小值；y向超高影響率隨著超高的增大呈現先上升然后下降的趨勢，且在超高值為60 mm時有極大值，180 mm有極小值；z向超高影響率隨著超高的增大呈現先上升再下降再上升的趨勢，且在超高為80 mm存在極大值，160 mm時存在極小值。

如圖9所示為齒輪箱測點2處(圓柱滾子軸承)在不同曲線參數下計算的振動加速度RMS值及超高影響率曲線圖。從圖9中可以看出，齒輪箱測點2處x向的振動加速度RMS值隨超高的變化趨勢與齒輪箱測點1總體相似，但有一點不同，齒輪箱測點1處半徑7 000 m的拐點為60 mm，齒輪箱測點2處半徑7 000 m的拐點為80 mm；y向振動加速度隨著超高和半徑的增大而增大；z向的振動加速度隨著超高值的增大呈現先增后減的趨勢，存在一個拐點，而且曲線半徑越小，拐點對應的超高值越大，如5 500 m曲線半徑的拐點為100 mm超高，7 000 m曲線半徑的拐點為60 mm超高。

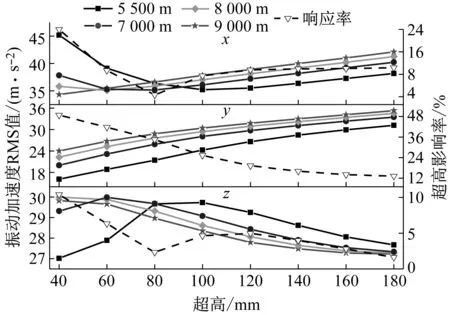
圖9 齒輪箱測點2(圓柱滾子軸承)Fig.9 Measuring point 2 of the gearbox(Cylindrical roller bearings)

從圖9所示的齒輪箱測點2處x，y，z方向上超高影響率變化曲線圖，可以看出x向超高影響率呈現先下降后上升最后趨于平緩的趨勢，且在超高值40 mm有極大值，超高值為80 mm有極小值；y向超高影響率呈現單調下降的趨勢，且在超高值為40 mm有極大值，180 mm有極小值；z向超高影響率呈現先下降再略有上升最后下降的趨勢，且在超高值為40 mm存在極大值，180 mm存在極小值。

如圖10所示為齒輪箱測點3處(四點球滾子軸承)在不同曲線參數下測得的振動加速度RMS值及超高影響影響率曲線圖。從圖10中可以看出，齒輪箱測點3(四點球軸承)在x，y，z三個方向均無明顯拐點，x向振動加速度隨著超高值的增大呈現先增后減的趨勢，在40～160 mm超高之間，振動加速度RMS值隨著半徑的減少而增大，在160～180 mm之間，振動加速度隨著半徑的增大而增大；y，z方向振動加速度隨著超高值和半徑的增大而增大。

從圖10所示的齒輪箱測點3處x，y，z方向上超高影響率變化曲線圖，可以看出x向超高影響率呈先下降后緩慢上升的趨勢，且在超高值為40 mm有極大值，超高值為160 mm有極小值；y向超高影響率呈現先上升后下降的趨勢，且在超高值為60 mm有極大值，180 mm有極小值；z向超高影響率呈現先下降再緩慢上升的趨勢，且在超高值為40 mm存在極大值，120 mm存在極小值。

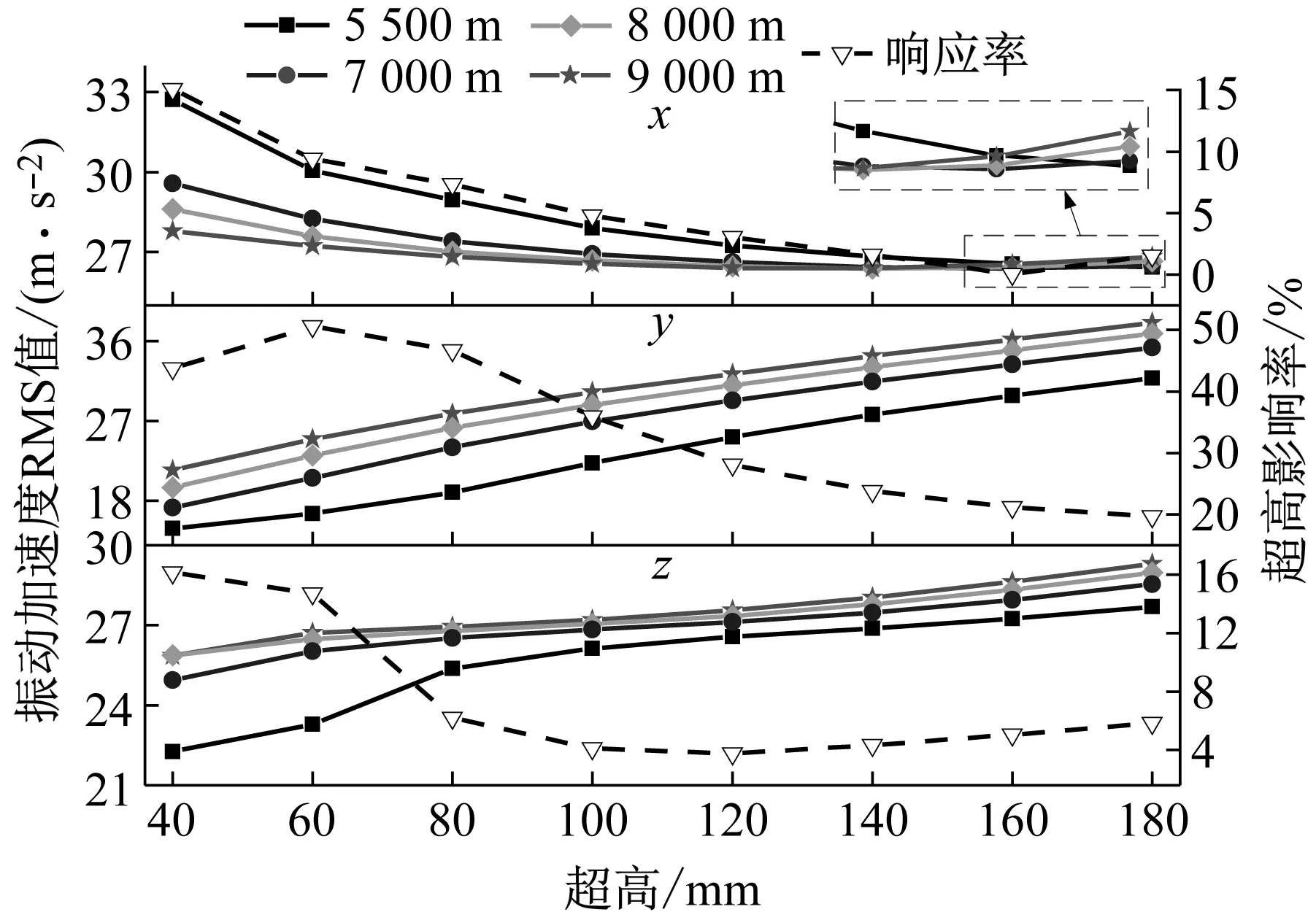
圖10 齒輪箱測點3(四點球軸承處)Fig.10 Measuring point 3 of the gearbox(Four-ball bearings)

如圖11所示為齒輪箱測點4處(左側圓錐滾子軸承)在不同曲線參數下測得的振動加速度RMS值及超高影響率曲線圖。從圖11中可以看出，齒輪箱測點4處x向振動加速度隨著半徑和超高值的增大而增大；y向振動加速度同樣隨著半徑和超高值的增大而增大；z向振動加速度隨著超高值和半徑的增大而減小。

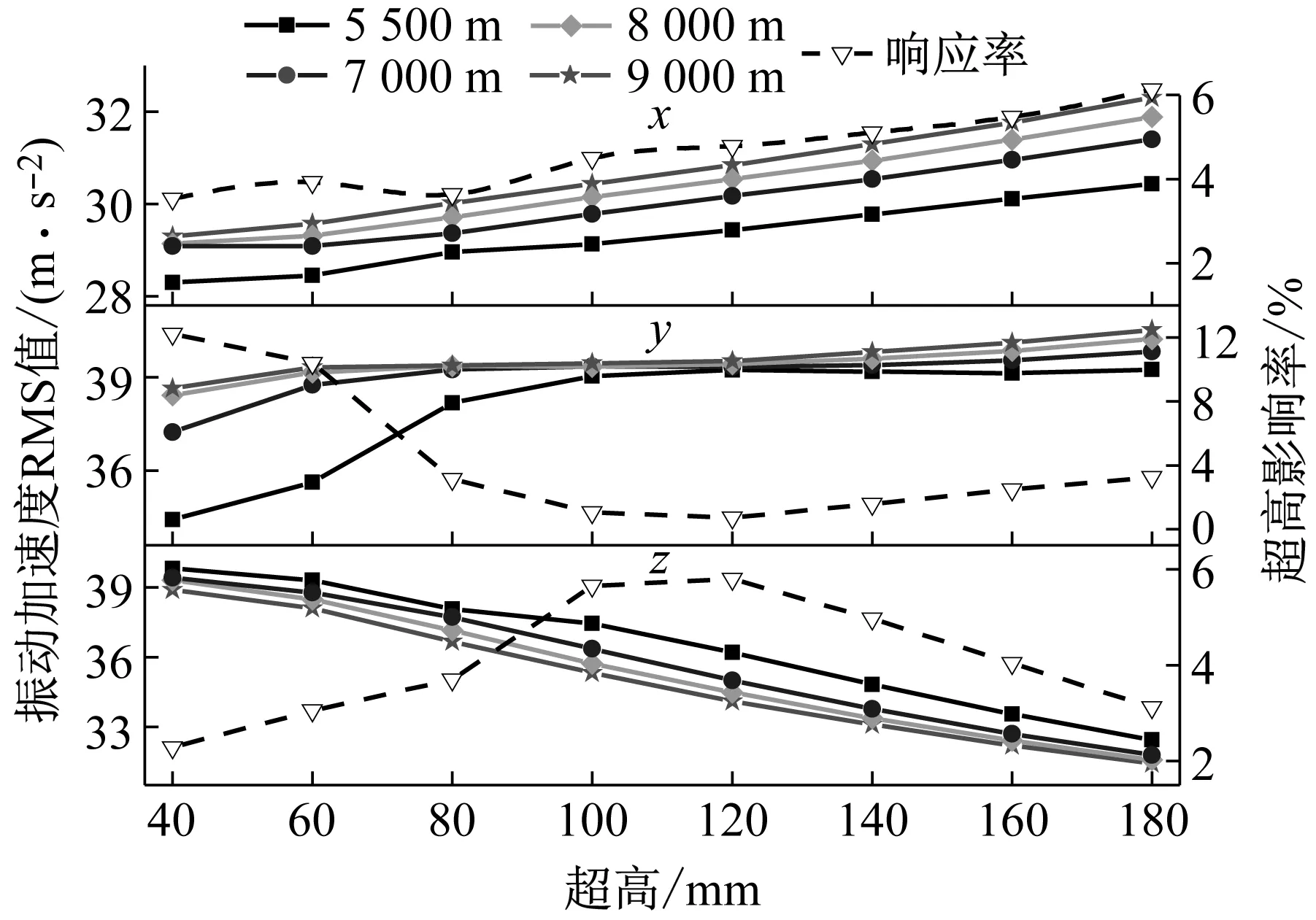
圖11 齒輪箱測點4(左側圓錐滾子軸承處)Fig.11 Measuring point 4 of the gearbox(Left tapered rolling bearing)

從圖11所示的齒輪箱測點4處x，y，z方向上超高影響率變化曲線圖，可以看出x向超高影響率呈現先增加后略有下降最后上升的趨勢，且在超高值為180 mm有極大值，超高值為40 mm有極小值；y向超高影響率呈現先下降后上升的趨勢，且在超高值為40 mm有極大值，120 mm有極小值；z向超高影響率呈現先上升再下降的趨勢，且在超高值為120 mm存在極大值，40 mm存在極小值。

如圖12所示為齒輪箱測點5處(右側圓錐滾子軸承)在不同曲線參數下測得的振動加速度RMS值及超高影響率曲線圖。從圖12中可以看出，齒輪箱測點5處x向振動加速度RMS值在超高值40～160 mm之間隨著超高值和半徑的增大而增大，在160～180 mm之間，振動加速度RMS值隨著超高的增大而增大，隨著半徑的減小而增大；y向振動加速度隨著超高值和半徑的增大而增大；z向振動加速度隨著超高值和半徑的增大而增大。從圖12所示的齒輪箱測點5處x，y，z方向上超高影響率變化曲線圖，可以看出x向超高影響率呈現先下降后略有上升的趨勢，且在超高值為40 mm有極大值，超高值為160 mm有極小值；y向超高影響率呈現先下降后上升最后下降的趨勢，且在超高值為40 mm有極大值，180 mm有極小值；z向超高影響率呈現先下降再上升的趨勢，且在超高值為40 mm存在極大值，120 mm存在極小值。

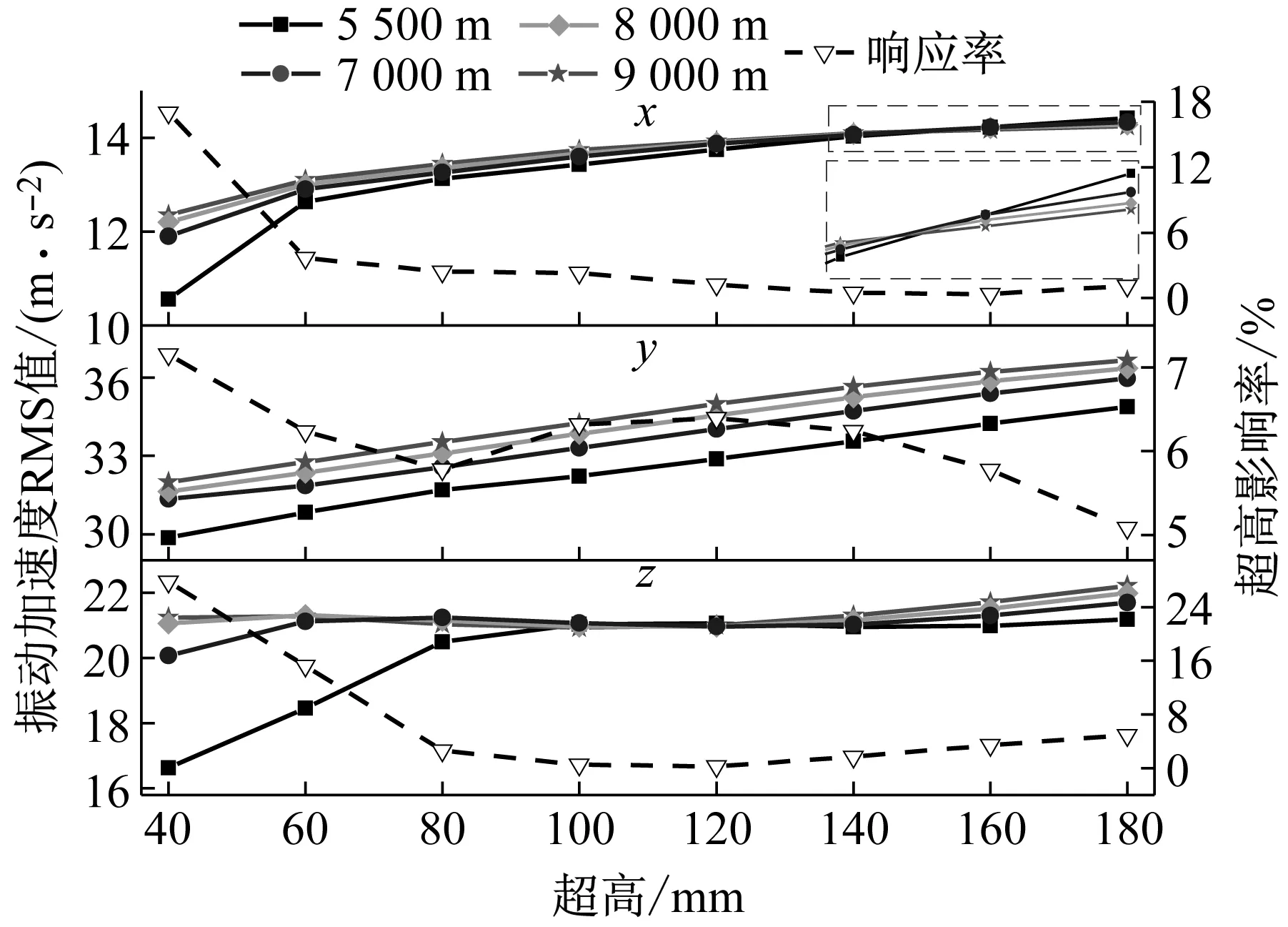
圖12 齒輪箱測點5(右側圓錐滾子軸承處)Fig.12 Measuring point 4 of the gearbox(Right tapered rolling bearing)

在一定超高范圍內，齒輪箱各測點超高影響率極值分布如圖13所示，從圖中可以看出齒輪箱各測點在y方向上，半徑的變化對振動加速度幅值的影響更強烈且在齒輪箱測點1，2，3處尤為明顯，影響率分別為33.5%、48.8%、50.6%；在x，z方向上，半徑的變化對振動加速度的影響程度相似但與y向相比影響程度較小。

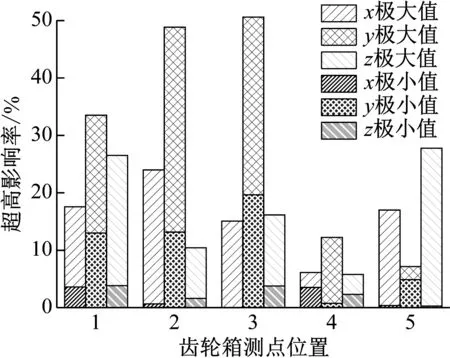
圖13 齒輪箱各測點超高影響率極值分布圖Fig.13 Extreme value distribution of the super elevation influence rate at each measuring point of the gearbox

如圖14所示為超高因子出現概率餅狀圖，圖14(a)中餅狀圖表示為出現超高影響率極大值對應的超高因子的概率，可以看出一半以上的齒輪箱測點的極大超高因子為超高值40 mm，說明在此超高值下，半徑的變化對齒輪箱各測點振動加速度RMS值影響程度較大；圖14(b)中餅狀圖表示為出現超高影響率極小值對應的超高因子的概率，可以看出有三分之一的齒輪箱測點的極小超高因子為超高值180 mm，說明在此超高值下，半徑的變化對振動加速度RMS值影響程度較小。

通過對齒輪箱吊桿支座及各軸承處在不同曲線參數下的振動加速度RMS值分析，發現齒輪箱各測點振動加速度變化規律呈現如圖15所示的分布情況。

當只考慮超高值對振動加速度RMS值的影響，齒輪箱測點振動加速度變化規律如圖15(a)分布情況1所示，虛線方框內(包括振動加速度測點1，2，3)，x向振動加速度RMS值隨超高變化曲線均存在拐點，振動加速度隨著超高值的增大呈現先減小后增大的趨勢；雙點劃線方框內(包括振動加速度測點4，5)，x向振動加速度不存在拐點，且振動加速度隨著超高的增大而增大；y向振動加速度變化情況均為隨著超高值的增大而增大；在z方向上，各測點振動加速度隨超高變化曲線略有差異，分布特點如圖15(b)分布情況2所示，虛線方框內(包括振動加速度測點1，2，4)，振動加速度隨著超高值的增加整體呈現下降的趨勢，雙點劃線方框內(包括振動加速度測點3，5)，振動加速度隨著超高值的增加整體呈現上升的趨勢。

當只考慮半徑值對振動加速度RMS值的影響，在x，z方向上，分布特點如圖15(a)分布情況1所示，在x方向上，虛線內各測點振動加速度大小隨著半徑的增大而增大；在z方向上；虛線內各點振動加速度大小隨著半徑的增大而減小，雙點劃線內各測點振動加速度隨半徑變化規律與黃色虛線內測點相反；在y方向上，各測點的振動加速度RMS值均隨半徑的增大而增大。

3.3 齒輪嚙合特性

本文關注的齒輪嚙合特性包括四個方面，分別是時變嚙合剛度，接觸應力，傳動誤差峰峰值和嚙合力。

如圖16所示為高速列車在通過9 000 m半徑曲線下，超高為40～100 mm齒輪副時變嚙合剛度的時域放大圖，可以看出在不同超高下齒輪副的時變嚙合剛度存在一個相位差，且相位差隨著超高值的增大而遞增，在幅值上有所不同但變化很小，為比較不同曲線通過特性對齒輪副時變嚙合剛度的影響，本文采用時變嚙合剛度的RMS值來分析研究。

圖16 時變嚙合剛度時域放大圖Fig.16 Time domain magnification of time-vary meshing stiffness

齒輪時變嚙合剛度的RMS值與曲線超高和半徑的關系如圖17所示，可以看出，齒輪時變嚙合剛度RMS值隨著超高值的增加呈現先增加再減小最后增加的趨勢，在超高值為60～160 mm范圍里，齒輪時變嚙合剛度的有效值隨著半徑的增大而逐漸減小，由于齒輪副嚙合剛度RMS值減小會使系統振動幅度增大，而且系統的固有頻率會隨著平均嚙合剛度的減小而減小[25-26]，故隨著超高值和半徑的增大，齒輪副的嚙合剛度的RMS值減小，會導致系統的振動幅值變大，但從數值來看，時變嚙合剛度RMS最小值為6.13×109N/m，最大為6.18×109N/m，變化率為0.82%，故超高和半徑對時變嚙合剛度的RMS值影響較小。

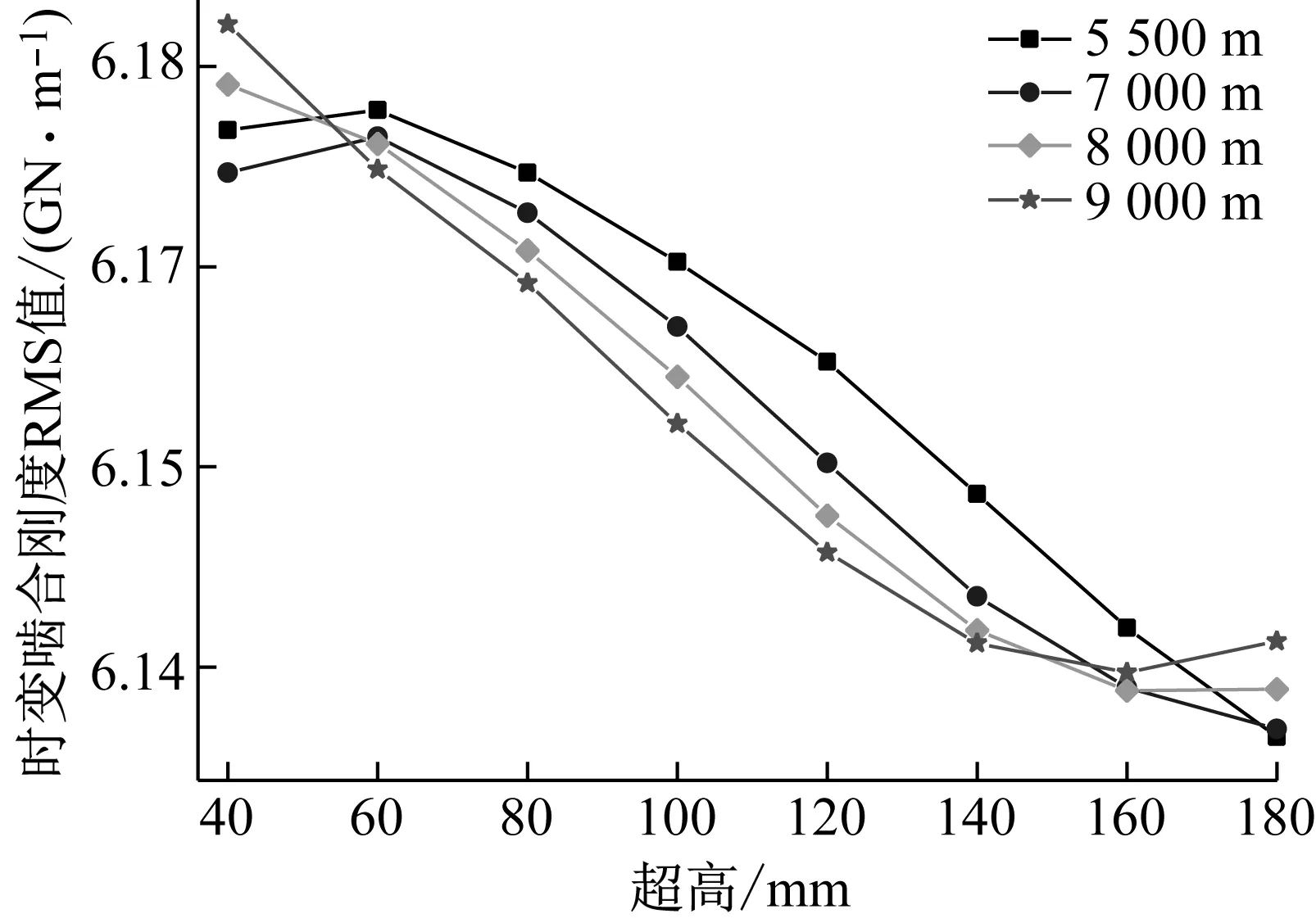
圖17 時變嚙合剛度RMS值Fig.17 RMS value of time-varying meshing stiffness

如圖18所示為齒輪副接觸應力與超高值和半徑的關系，可以看出接觸應力隨著超高值的增大而逐漸減小，隨著半徑的減小而逐漸增大，且半徑值對接觸應力RMS值的影響隨著超高值的增大而逐漸減弱，具體來看，在同一超高值40 mm下，列車駛經曲線半徑5 500 m時，齒輪接觸應力有最大值，最大值為597.5 MPa，半徑9 000 m時，齒輪接觸應力有最小值，最小值為584.6 MPa，變化率為2.2%；在同一曲線半徑5 500 m下，超高值為40 mm時，齒輪接觸應力有最大值597.5 MPa，超高值為180 mm時，齒輪的接觸應力有最小值572 MPa，變化率為4.3%。

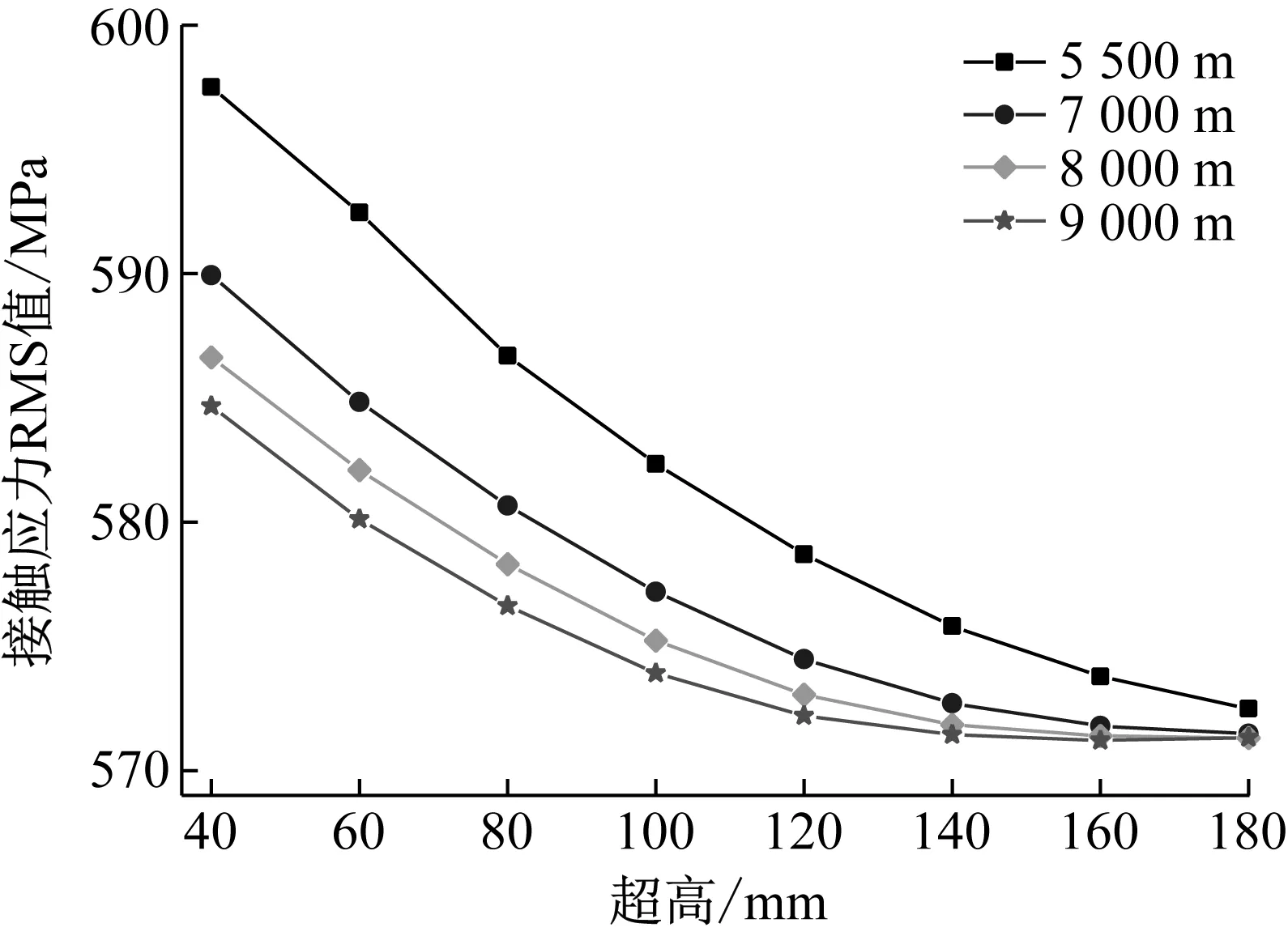
圖18 接觸應力RMS值Fig.18 RMS value of contact stress

如圖19所示為齒輪傳動誤差峰峰值與半徑和超高值的關系，從圖中可以看出，齒輪副傳動誤差峰峰值隨著超高值呈現先減小后增加的趨勢，存在拐點，且拐點對應的超高值隨著半徑的減小而增大，在超高為40～100 mm范圍內，傳動誤差峰峰值隨著半徑的減小而增大，在超高值160～180 mm范圍內，傳動誤差峰峰值隨著半徑的增大而增大，從數據來看，在超高值為40 mm時，5 500 m半徑與9 000 m半徑對應的傳動誤差峰峰值存在最大差值，差值為0.998 μm，變化率為23.9%；在半徑為9 000 m時，超高值為40 mm與180 mm對應的傳動誤差峰峰值存在最大差值，差值為1.482 μm，變化率為35.55%，從變化率來看，半徑和超高值的變化對傳動誤差峰峰值RMS值影響程度較大，此外傳動誤差是影響列車運行時，產生齒輪嘯叫的主要原因[27]，所以當列車曲線通過較大超高值的半徑時，齒輪副的嘯叫程度也會增大。

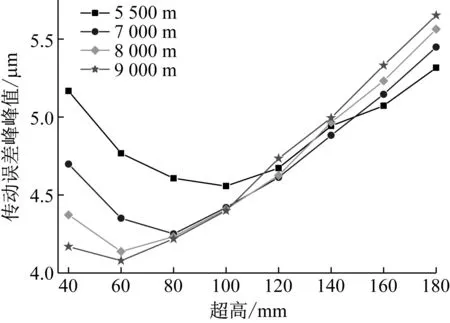
圖19 傳動誤差峰峰值Fig.19 Transmission error peak-peak value

斜齒輪在嚙合傳動的過程中，齒輪副之間相互作用的嚙合力，可分解為軸向力，徑向力和圓周力。如圖20所示為不同曲線參數對這三種力的影響曲線，從圖中20(a)和(c)可以看出超高值和半徑對齒輪副的軸向力和圓周力影響趨勢相似，都隨著超高值的增大呈現先減小后增加的趨勢，從幅值差值來看，軸向力最大差值為0.4 N，圓周力最大差值為1.5 N，所以超高和半徑的變化對軸向力與圓周力的幅值影響不大；如圖20(b)所示為徑向力隨超高和半徑的變化曲線，可以看出徑向力隨著超高值和半徑的增大而增大，且徑向力大小與超高值和半徑呈線性相關，超高影響下，徑向力變化率最大為7.2%，半徑影響下，徑向力變化率最大為3.2%，從變化率來看，半徑和超高的變化對徑向力幅值比對軸向力和圓周力幅值影響較大。

(a)

(b)

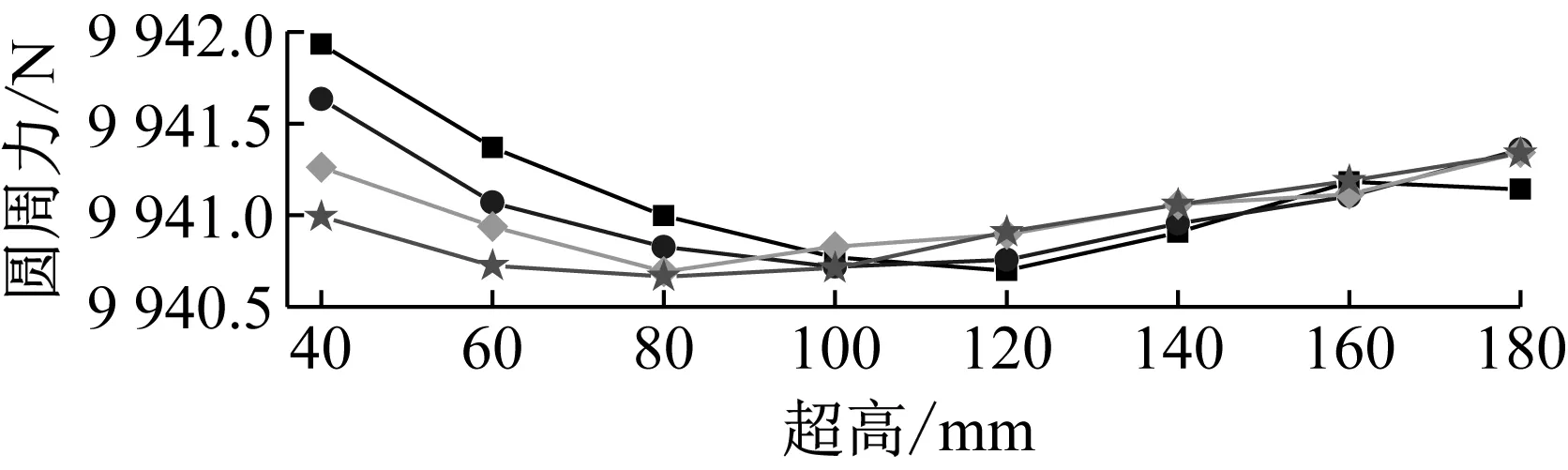
(c)圖20 齒輪嚙合力RMS值Fig.20 RMS value of gear meshing force

4 結 論

通過建立高速列車牽引齒輪傳動系統車軌耦合模型對高速列車曲線通過進行仿真，獲得不同曲線通過參數對高速列車齒輪傳動系統動力學響應數據，分析數據得到如下結論。

(1) 超高值與曲線半徑變化對齒輪箱振動加速度影響呈現分區特征。總的來看，當超高值為變量時，齒輪箱輸入軸承處和吊桿處的振動加速度隨著超高值的增加而增加，齒輪箱輸出軸承處振動加速度變化規律則相反；當曲線半徑為變量時，齒輪箱左側軸承及吊桿處的振動加速度隨著曲線半徑的增大而增大，齒輪箱右側軸承處振動加速度變化規律則相反。

(2) 曲線半徑變化對齒輪箱各測點y向振動加速度影響較大，對x，z向振動加速度影響較小，且在超高值為40 mm時，曲線半徑變化對齒輪箱大部分測點振動加速度影響較大，在超高值為180 mm時，曲線半徑變化對齒輪箱大部分測點振動加速度影響較小。

(3) 隨著超高值增大，齒輪副時變嚙合剛度和接觸應力逐漸減小，傳動誤差峰峰值逐漸增加，但超高值和曲線半徑的變化對時變嚙合剛度和接觸應力幅值變化影響較小，對傳動誤差峰峰值幅值變化影響程度很大；軸向力和圓周力隨著超高的增加呈現先減后增的趨勢，徑向力隨著超高和半徑的增大呈現單調增加的趨勢，曲線半徑和超高變化對軸向力與圓周力幅值變化影響很小，對徑向力幅值變化影響較大。