沖擊荷載下鋼筋混凝土缺口梁破壞模式的試驗研究

宋 敏, 王志勇, 張 杰, 高士武, 王志華

(1. 太原理工大學 機械與運載工程學院, 應用力學研究所, 太原 030024; 2. 青海大學 土木工程學院， 西寧 810016)

鋼筋混凝土梁作為建筑工程中被廣泛應用的結構，在地震、爆炸、車橋碰撞、飛機撞擊剛性墻等沖擊荷載下的安全性能受到日益關注[1-4]。許多學者利用落錘沖擊試驗機對無缺口鋼筋混凝土梁進行動態三點彎試驗，研究了配筋率[5]、沖擊速度[6-7]對試件承載性能和能量耗散的影響。Fu[8-9]采用支反力峰值以評估沖擊荷載下試件的承載性能。為了合理估算試件破壞過程中消耗的能量，趙德博等[10]對支反力-跨中位移曲線進行積分得到梁整體變形耗能。隨著沖擊速度的提高，試件破壞消耗能量與錘頭動能的比值逐漸減小，梁由彎曲破壞逐漸轉變為剪切破壞。通過對比不同破壞模式下鋼筋混凝土梁的耗能，Kishi等[11-12]將支反力-跨中位移曲線簡化為平行四邊形或三角形后提出了靜態抗彎/抗剪承載力關于沖擊能量和跨中殘余撓度的經驗公式。朱翔等[13]對鋼筋混凝土柱進行橫向沖擊試驗后發現試件斷為兩截且軸壓比的增大導致試件殘余變形增大。除試驗研究外，一些學者采用數值模擬的方法對沖擊荷載下鋼筋混凝土梁的結構響應和斷裂過程進行了分析。Ozbolt等[14]利用數值模擬研究了鋼筋混凝土梁的裂縫形態，結果表明剪力筋存在時裂縫分布均勻。Al-Thairy等[15]提出用于計算橫向沖擊下鋼筋混凝土柱臨界沖擊速度的解析方法。目前已有許多關于完整鋼筋混凝土結構的試驗、數值模擬研究工作，對含缺口試件的沖擊響應研究較少。

然而在實際工程中，受外界荷載和溫度變化影響，鋼筋混凝土梁內部的微裂紋、孔隙逐漸衍生擴展致使混凝土開裂。裂縫導致鋼筋混凝土梁內部應力再分布，引起結構承載力和破壞模式的改變[16-17]。沖擊荷載下完整鋼筋混凝土梁底部往往產生多條彎曲裂縫甚至剪切裂縫[18]。與完整的鋼筋混凝土梁相比，沖擊荷載下含缺口梁更容易破壞，其承載力和破壞模式也與沖擊速度有關。

采用已有經驗公式[19-20]無法有效評估動態加載下鋼筋混凝土缺口梁的承載力和能量耗散。因此，開展沖擊荷載下鋼筋混凝土缺口梁的破壞模式和力學行為研究十分必要。本文利用落錘式沖擊試驗機對不同配筋率的鋼筋混凝土缺口梁進行動態三點彎試驗，與靜態試驗結果對比后討論了沖擊速度對試件承載力、變形耗能的影響。基于試驗結果建立的靜態抗彎/抗剪承載力與沖擊能量和跨中位移的經驗公式，對鋼筋混凝土缺口梁的安全性能評估具有一定的工程指導意義。

1 試驗概況

1.1 試件設計

為研究沖擊速度對不同配筋率鋼筋混凝土梁力學性能的影響，試驗設計3種具有相同尺寸的含預制缺口鋼筋混凝土梁，如圖1所示。試件截面尺寸為150 mm×150 mm(b×h)，混凝土梁長度為800 mm(L)，跨度為600 mm(S)，預制缺口尺寸為45 mm×4 mm(a0×d)，鋼筋橫截面圓心至梁底部和側面距離均為30 mm(c=30 mm，m=30 mm)，相鄰鋼筋圓心間距為30 mm(n)。混凝土各組分質量配合比為1∶0.35∶2.62∶1.55(水泥∶水∶石子∶砂)。對150 mm×150 mm×150 mm的立方體試塊進行單軸壓縮試驗后測得混凝土立方體抗壓強度為63.79 MPa。試驗設計方案如表1所示，梁底部分別配置直徑12 mm的HRB335級鋼筋，試件配筋率(ρ)為0.50%，1.00%，2.01%，且分別標記為S1, S2, S4。靜態拉伸試驗中鋼筋屈服強度為386.7 MPa，極限強度為632.3 MPa，彈性模量為200 GPa，極限應變為0.156。通過對試件進行靜態三點彎試驗可測得靜態抗彎承載力(Pu)。我國設計規范中利用Vu=1.75ftbh0/(λ+1)計算得到不含缺口的無腹筋鋼筋混凝土梁靜態抗剪承載力(Vu)，其中剪跨比為λ=S/2h0，ft=0.1fc，h0為截面有效高度。無缺口鋼筋混凝土梁的截面有效高度為試件高度與鋼筋保護層厚度的差。本文中預制缺口高度為a0，因此截面有效高度為：h0=h-a0，代入后得到Vu=1.75ftb(h-a0)/(λ+1)。

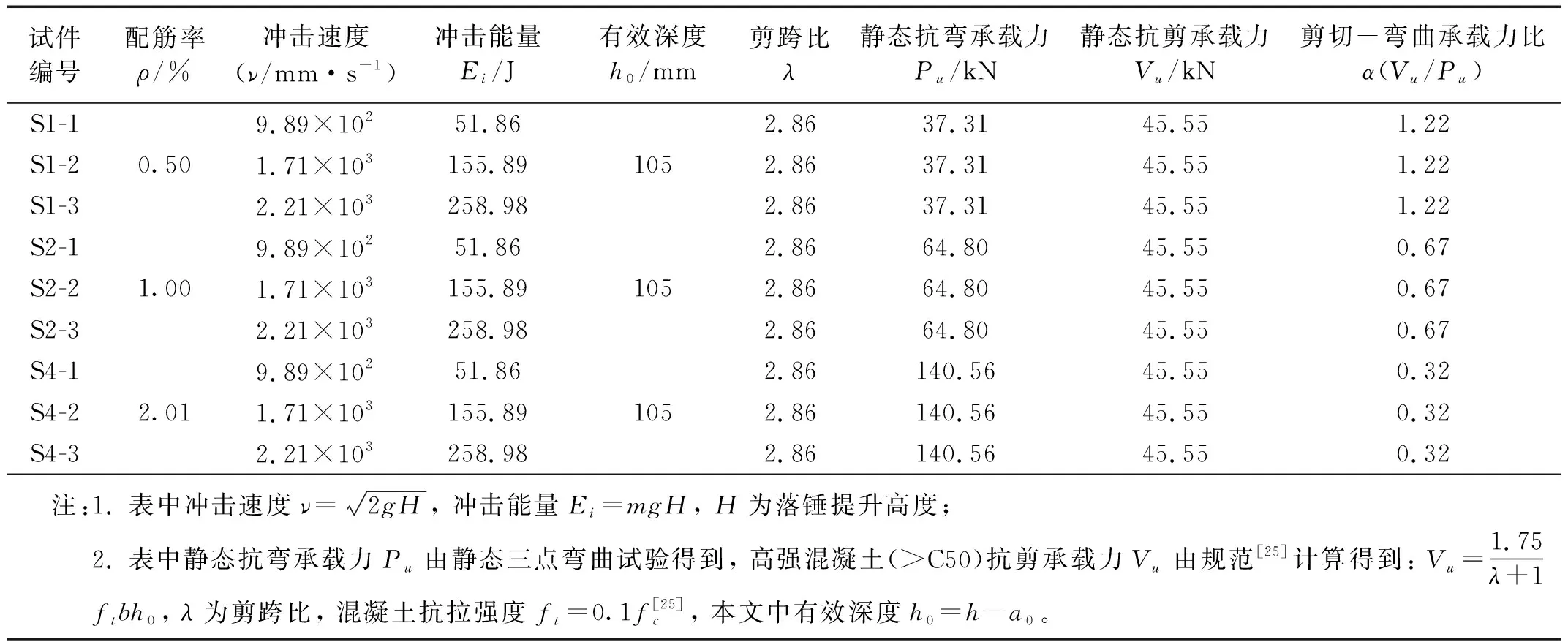
表1 試件設計一覽表Tab.1 The list of specimen design

1.2 試驗裝置及方案

準靜態試驗采用青海大學土木工程學院自平衡反力架試驗機進行加載，試驗裝置和數據采集設備如圖2所示。靜態加載試驗機最大推力為 300 kN，行程可達500 mm。力信號采用DH3818靜態測試應變儀進行采集，采樣頻率為1 Hz。

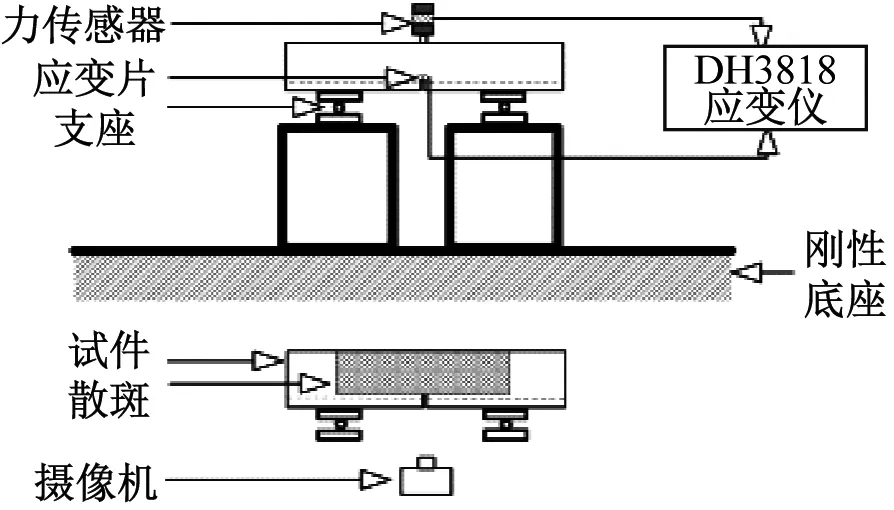
圖2 靜態試驗裝置圖Fig.2 Schematic of static experiment setup

動態試驗采用青海大學落錘沖擊試驗機進行，試驗裝置和數據采集設備如圖3所示。落錘沖擊過程中，錘頭形狀僅影響沖擊點區域的局部損傷，對于裂縫擴展和結構響應(沖擊力、支反力、跨中位移時程曲線)影響很小[22]。本次試驗采用質量106.05 kg，直徑100 mm的平面圓形錘頭。為了在試驗中實現跨中加載和能量損失的減少，在梁上表面跨中位置放置剛性墊塊(30 mm×30 mm×150 mm)。試驗中通過改變落錘沖擊高度(50 mm、150 mm和250 mm)對鋼筋混凝土缺口梁進行三種沖擊速度的三點彎曲試驗，相應的沖擊速度分別為9.89×102mm/s，1.71×103mm/s，2.21×103mm/s。在錘頭與配重之間及兩個支座處安裝動態力傳感器以測量沖擊力和支反力。在鋼筋中心處粘貼應變片以監測梁破壞過程中鋼筋的應變。沖擊力、支反力和鋼筋應變信號用示波器進行采集，采樣頻率為2 MHz。為了研究沖擊速度對跨中位移的影響，試驗前在混凝土預制缺口上方局部區域噴繪散斑，并利用I-Speed 716高速相機記錄試件破壞過程，高速相機采樣幀率為50 kHz。加載結束后利用Digital Image Correlation(DIC)技術分析散斑區域的位移場得到沖擊過程中不同時刻的跨中位移值。許多學者利用DIC測量試件的位移、變形和應變場[23-24]。對預制缺口上方局部位移場的分析為進一步研究起裂荷載、裂紋擴展速度等參數提供參考。本文主要討論鋼筋混凝土缺口梁的抗沖擊性能，對局部區域裂紋的起裂未做詳細描述。

2 試驗結果與分析

2.1 破壞形態

低速沖擊下無缺口鋼筋混凝土梁發生彎曲破壞時，梁底部往往產生多條裂縫。對含裂縫的鋼筋混凝土梁進行不同沖擊速度下的動態三點彎試驗后，試件的破壞形態如圖4所示。沖擊速度為9.89×102mm/s時，配筋率為0.50%的試件預制缺口根部應力迅速增大，裂紋起裂后應力釋放，梁表面形成單一的裂紋且擴展過程中無微裂紋產生。由于混凝土內部骨料尺寸、位置的隨機性，裂紋起裂后曲折擴展至加載點附近，試件發生彎曲破壞。當配筋率大于0.50%時，由于沖擊能量較小，沖擊過程中試件表面未出現裂紋，試件始終處于彈性變形階段。沖擊速度為1.71×103mm/s時，配筋率為0.50%混凝土梁表現出與9.89×102mm/s工況下相同的裂紋形態，且裂紋寬度增大；其他配筋率試件的裂紋從預制缺口根部起裂后擴展長度較小，且隨著錘頭與試件的分離沖擊力開始卸載，鋼筋部分彈性變形恢復導致裂縫閉合，沖擊結束后裂紋不可見。沖擊速度為2.21×103mm/s時，低配筋率試件發生彎曲破壞只有一條主裂紋；隨著配筋率的提高，加載點下方的裂紋擴展長度逐漸減小，且試件表面出現八字型剪切裂紋，破壞模式轉變為彎曲-剪切破壞。

沖擊速度較低時，低配筋率混凝土梁發生彎曲破壞，裂紋從預制缺口根部附近起裂后擴展至加載點；增大配筋率后梁處于彈性變形，裂紋起裂后隨著外載荷的卸載發生閉合。隨著沖擊速度和配筋率的提高，預制缺口附近的裂紋擴展受到抑制，剪切裂紋產生，試件由彎曲破壞轉變為彎剪破壞。

Kishi等對無腹筋的完整鋼筋混凝土梁進行不同沖擊速度的三點彎試驗后發現，靜態剪切-彎曲承載力比(α)小于1時，試件發生剪切破壞；α大于1時低速沖擊(1×103mm/s，3×103mm/s)下發生彎曲破壞，沖擊速度增大時(v=5×103mm/s)發生剪切破壞。本文中靜態剪切-彎曲承載力比小于1(ρ=1.00%,ρ=2.01%)的試件在沖擊速度為9.89×102mm/s和1.71×103mm/s時發生彎曲破壞；沖擊速度增大時出現剪切裂紋。α大于1(ρ=0.50%)的試件在不同沖擊速度下均發生彎曲破壞，單條裂紋從缺口根部處起裂擴展至加載點。由此可見，鋼筋混凝土含缺口梁的破壞模式與靜態剪切-彎曲承載力比和沖擊速度有關，且與完整鋼筋混凝土梁有所不同。綜上所述，沖擊速度小于2.21×103mm/s時，α>1的鋼筋混凝土缺口梁發生彎曲破壞；沖擊速度小于1.71×103mm/s時，α<1的試件發生彎曲破壞，當沖擊速度增大至2.21×103mm/s時發生彎剪破壞。

2.2 沖擊力和支座反力時程曲線

沖擊荷載作用下，當錘頭與試件接觸時沖擊力迅速達到最大值并減小，這一階段試件幾乎未發生變形，沖擊力基本被慣性力抵消，此時的沖擊力主要用于梁的加速。Kishi等認為支反力不受梁體自身慣性效應的影響，較沖擊力更能反映構件自身的抗沖擊性能。

沖擊荷載下含缺口鋼筋混凝土梁的沖擊力時程曲線表現出與完整梁不同的變化趨勢。付應乾等對完整鋼筋混凝土梁進行不同沖擊速度的試驗以分析其結構響應和斷裂過程。沖擊荷載下完整鋼筋混凝土梁的沖擊力時程曲線具有峰值階段、平臺階段和衰減階段。錘頭與鋼筋混凝土梁初次接觸時混凝土響應占主導，沖擊力迅速增大至最大值。隨著錘頭與混凝土梁上表面分離沖擊力開始減小。當錘頭與試件再次接觸時鋼筋變形逐漸趨于穩定，沖擊力震蕩并趨于水平平臺發展，梁底部產生彎曲裂紋且向上擴展。隨著錘頭反復卸載，試件開裂形成彎曲裂紋或剪切裂紋以釋放能量，沖擊力開始衰減并逐漸減小至0。

典型的含缺口鋼筋混凝土梁在落錘沖擊下的沖擊力、跨中位移、鋼筋應變和缺口根部裂紋張開位移時程曲線如圖5所示。沖擊速度為1.71×103mm/s時，錘頭與試件接觸后沖擊力增大至最大值并隨著錘頭卸載減小至0，此時梁跨中位移和裂紋張開位移均為0表明梁體未發生變形。與完整混凝土梁相比，含缺口梁中鋼筋應變的觸發提前且與沖擊力第一峰值同一時刻到達最大值。這是由于沖擊荷載下完整鋼筋混凝土梁底部混凝土先受拉，隨后傳遞應力至鋼筋與混凝土的粘結區域，而含缺口混凝土梁跨中下半部分鋼筋直接承載。

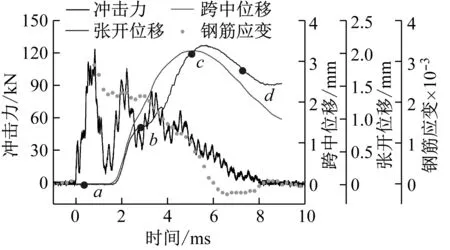
圖5 鋼筋混凝土缺口梁的沖擊力、跨中位移、裂紋張開位移和鋼筋應變時程曲線(ρ=0.50%, v=1.71×103 mm/s)Fig.5 The time curves of impact force, mid-span displacement, crack opening displacement and steel strain for notched reinforced concrete beam whose reinforcement ratio was 0.50% when the impact velocity was 1.71×103 mm/s

隨著錘頭與試件再次接觸，沖擊力、跨中位移開始增大。試件預制缺口根部附近應力迅速增大導致混凝土開裂釋放部分能量，裂紋張開位移逐漸增大。這一階段試件跨中位移增大，試件變形加劇導致裂紋張開位移增大，而鋼筋應變逐漸減小表明鋼筋部分彈性變形恢復并抑制裂紋繼續擴展。由于兩種機制的相互作用，沖擊力平臺階段并不明顯而是呈現震蕩減小的趨勢。當跨中位移達到最大值時，錘頭反彈同時試件部分彈性變形恢復導致跨中位移開始減小，而裂紋張開距離也呈現出先增大后減小的變化趨勢。由圖5可知，一定沖擊速度下隨著配筋率的提高，鋼筋應變平臺趨于明顯導致沖擊力的平臺階段顯著。隨著鋼筋變形和裂紋擴展釋放能量，沖擊力逐漸衰減至0。含缺口鋼筋混凝土試件沖擊力的衰減階段與完整試件差別較小。

利用DIC對預制缺口上方混凝土表面水平方向位移場處理后得到裂紋擴展過程如圖6所示。利用DIC提取缺口根部兩個相鄰點的水平方向位移差(UN-UM)得到缺口根部裂紋張開位移時程曲線。沖擊力增長階段，缺口附近裂紋張開位移為0。由圖6(a)可知，T=0.86 ms時，缺口上方區域位移場均勻且各點水平位移為0。當T=2.92 ms時，隨著沖擊力再次增大，梁體變形加劇，裂紋擴展明顯。裂紋擴展過程中由于鋼筋彈性變形恢復導致鋼筋對裂紋張開的抑制作用增強，裂紋張開位移速度減緩，如圖6(c)。當T=6.96 ms時，隨著跨中位移的減小與鋼筋變形趨于恒定，裂紋張開位移逐漸減小。

與完整鋼筋混凝土梁相比，含缺口試件的沖擊力時程曲線的三階段并不明顯。這是沖擊荷載下缺口根部應力集中導致裂紋更容易起裂釋放能量，裂紋擴展與鋼筋彈性變形恢復共同作用導致的。

本文對不同配筋率的鋼筋混凝土缺口梁進行三種沖擊速度的三點彎試驗，試驗中測得到錘頭沖擊力、兩支座支反力之和、加載點下方鋼筋應變如圖7所示。對比不同沖擊速度下的沖擊力可知，錘頭與試件接觸后沖擊力迅速增大且出現一個平臺，隨后震蕩減小至零。配筋率一定時，隨著沖擊速度的增大，鋼筋混凝土梁的沖擊力震蕩加劇，且沖擊力峰后平臺隨著配筋率的增大更加明顯。

不同沖擊速度下，裂紋擴展過程時鋼筋受拉伸作用開始變形，鋼筋應變逐漸增大；當錘頭卸載時鋼筋彈性變形恢復，應變開始減小，裂紋產生閉合。配筋率為0.50%試件中鋼筋的應變峰值隨著沖擊速度的提高逐漸增大，沖擊速度大于9.89×102mm/s時應變峰值超過屈服應變，表明鋼筋發生屈服。沖擊速度一定時，隨著配筋率的提高，單根鋼筋應變相對減小。這是由于配筋率的增大導致試件破壞模式改變，鋼筋有效抑制了加載點下方裂紋的起裂和擴展，預制缺口附近的鋼筋變形相對減少。

不同沖擊速度下，與沖擊力相比支反力幾乎沒有震蕩，且不同配筋率試件的支反力隨時間變化均呈現半正弦波的變化趨勢。不同沖擊速度下試件的支反力最大值如圖8所示。沖擊速度為9.89×102mm/s時，不同配筋率混凝土梁的支反力最大值幾乎相同，結果表明沖擊速度小于1 m/s時提高配筋率對試件支反力峰值影響較弱。沖擊速度為1.71×103mm/s時，支反力峰值隨著沖擊速度提高而增大。配筋率為0.50%試件支反力峰值的增長較弱，這是由于主裂紋從預制缺口根部附近起裂后擴展至加載點，試件已經發生破壞。配筋率為1.00%和2.01%的試件支反力在沖擊速度為1.71×103mm/s時幾乎一致。當沖擊速度增大至2.21×103mm/s時增大配筋率可有效提高試件承載力。

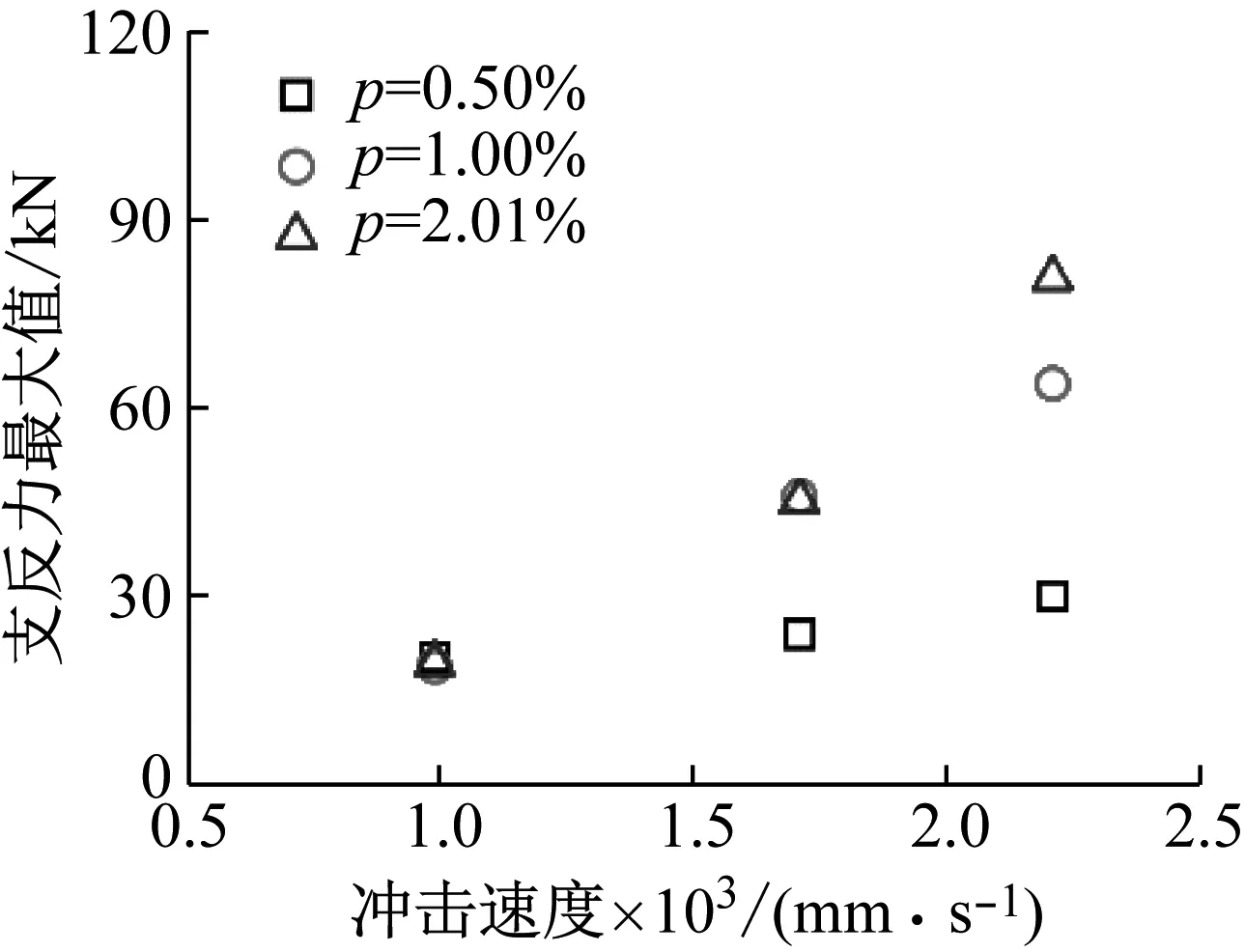
圖8 最大支反力與沖擊速度的關系Fig.8 The maximum of reaction force versus impact velocities

為研究沖擊荷載下鋼筋混凝土缺口梁支反力最大值與靜態抗彎(抗剪)承載力的動態響應比，本文對試件進行靜態試驗后測得不同配筋率試件的最大承載力分別為37.31 kN、64.80 kN和140.56 kN，得到動態響應比與沖擊速度的關系如圖9所示。Kishi等對無缺口鋼筋混凝土梁進行動態三點彎試驗后發現靜態剪切-彎曲承載力比(α)大于1時試件發生彎曲破壞；α小于1時發生剪切破壞。本文中配筋率為0.50%的混凝土梁在三種沖擊速度下的靜態剪切-彎曲承載力比(α)均大于1，沖擊荷載下只有單條裂紋從預制缺口根部處起裂，試件發生彎曲破壞。彎曲破壞型試件支反力最大值與靜態抗彎承載力的比值隨沖擊速度的變化如圖9(a)所示，對試驗結果進行擬合后得到式(1)

(1)

式中：Rmax為支反力；Pu為靜態抗彎承載力；ν為沖擊速度。

配筋率為1.00%和2.01%混凝土試件的α均小于1，沖擊過程中試件表面出現彎曲裂紋和剪切裂紋，彎剪破壞型試件支反力峰值與靜態抗剪承載力的比值隨沖擊速度的變化如圖9(b)所示，進行線性擬合后得到式(2)

(2)

式中，Vu為靜態抗剪承載力。

在本文沖擊速度范圍內，鋼筋混凝土缺口梁發生彎曲破壞或彎剪破壞。上述經驗公式可預估一定沖擊速度范圍內鋼筋混凝土缺口梁的承載性能，為梁構件的安全性能評估提供一定的參考價值。

2.3 梁的能量耗散

不同配筋率混凝土梁在三種沖擊速度下的支反力-跨中位移曲線(R-δ)和跨中位移時程曲線如圖10和圖11所示。沖擊過程中不同配筋率混凝土梁跨中位移在沖擊荷載下逐漸增大，當錘頭卸載時鋼筋部分彈性變形恢復，跨中位移到達峰值后開始遞減。由圖7中支反力可知，不同沖擊速度下試件的支反力先增大后減小，呈現為半正弦波波形。因此支反力-跨中位移曲線呈環狀曲線。配筋率為0.50%時，隨著沖擊速度的提高，支反力最大值變化不明顯，而跨中最大位移和殘余位移顯著增大。配筋率為1.00%和2.01%時，支反力最大值和最大位移均隨沖擊速度提高顯著增大。

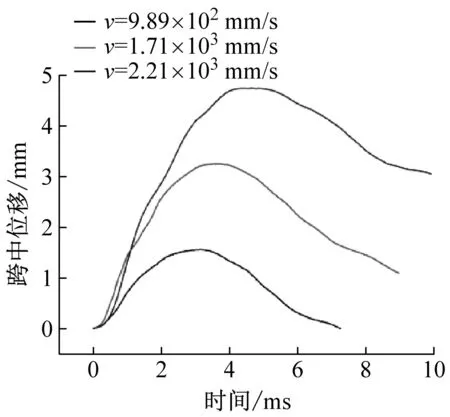
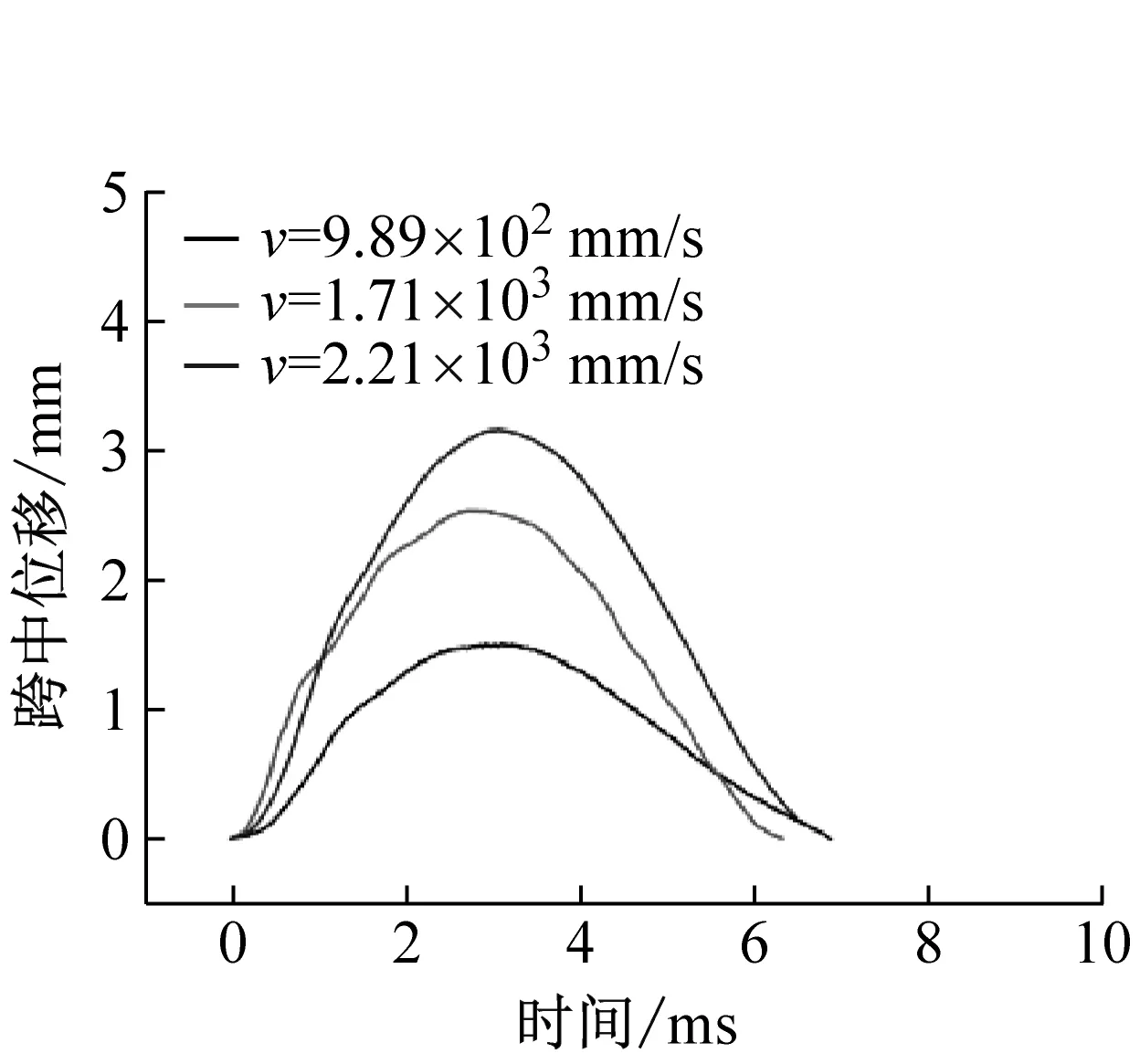
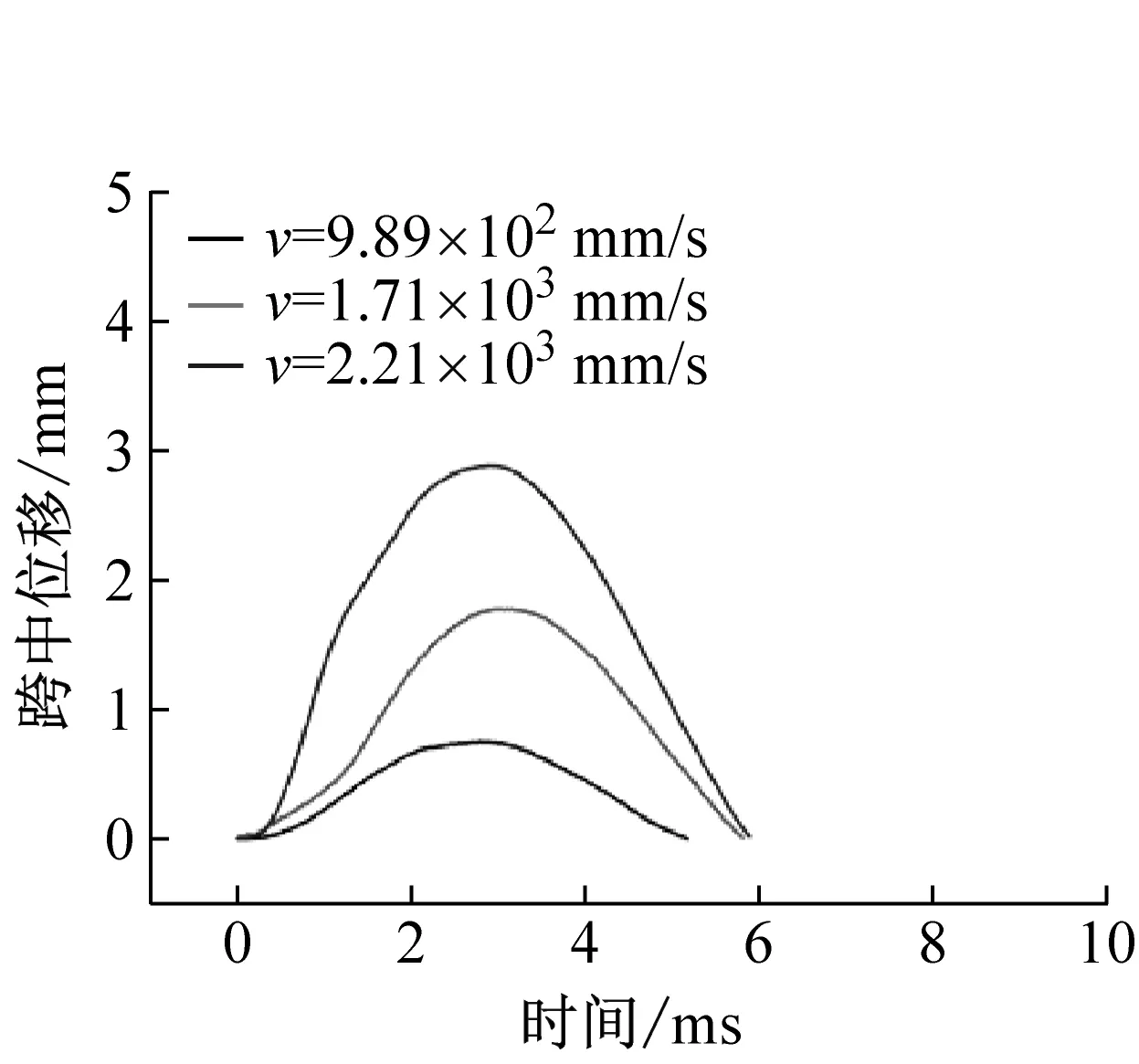
圖10 跨中位移時程曲線Fig.10 The time curves of mid-span displacement.

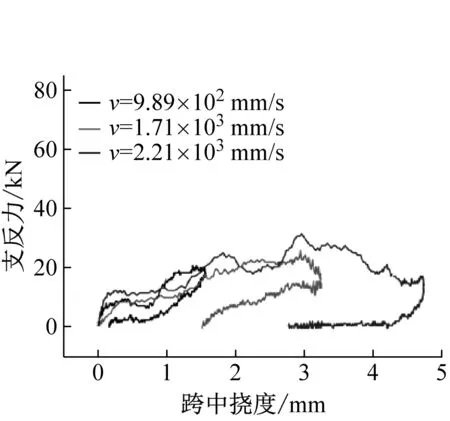
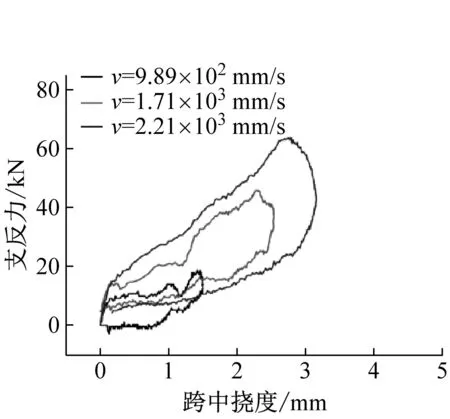
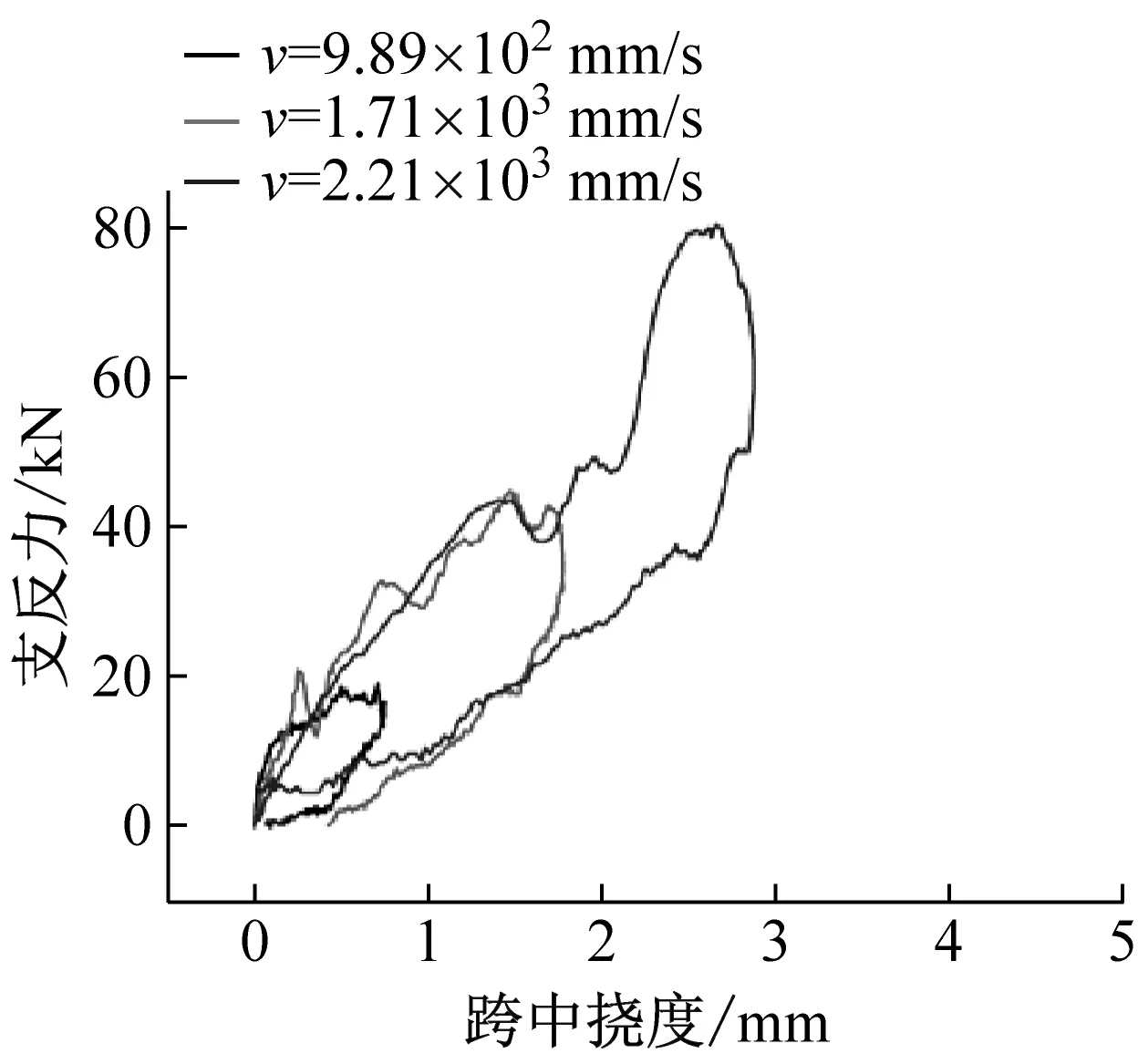
圖11 支反力-跨中位移曲線Fig.11 The curves of reaction force versus mid-span displacement.

沖擊過程中，一部分沖擊能量用于試件加速，另一部分用于試件變形。梁的能量耗散是指梁在一次加載過程中試件破壞消耗的能量，對支反力-跨中位移曲線進行積分可得到梁整體變形耗能。本文以試件破壞吸收的能量(Ek)和落錘動能(Ei)的比值為縱軸，沖擊速度為橫軸來分析鋼筋混凝土缺口梁破壞吸收能量占比與沖擊速度的關系，如圖12所示。落錘動能為：Ei=

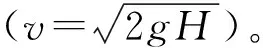
Ek/Ei=0.25

(3)

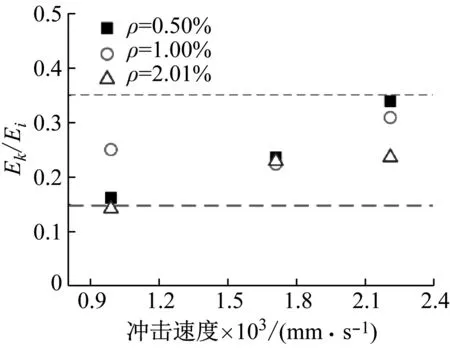
圖12 吸收能量與輸入能量的比(Ek/Ei)Fig.12 The ratio between absorbed energy and input energy

2.3.1 彎曲破壞

由不同沖擊速度下試件的破壞形態和靜態抗剪-抗彎承載力比值可知，沖擊荷載下配筋率為0.50%的鋼筋混凝土缺口梁發生彎曲破壞。圖11中，配筋率為0.50%的試件的支反力-跨中位移曲線近似于平行四邊形。如圖13(a)，假定彎曲破壞時試件的R-δ曲線為平行四邊形，曲線面積為彎曲破壞時試件的耗能(Ekb)

Ekb=Rmaxδrd

(4)

式中：δrd為試件的殘余位移；Rmax為支反力最大值。對簡化模型計算得到梁(ρ=0.50%)的吸收能量和支反力-跨中位移曲線積分結果對比后發現，不同沖擊速度下計算值比試驗值分別增大了12.34%、12.69%、3.82%。誤差在可允許范圍內，該簡化模型有效。將式(3)和(4)代入到式(1)中可得

(5)

整理后

(6)

利用式(6)可推導彎曲破壞型鋼筋混凝土缺口梁在一定沖擊能量下所需的靜態抗彎承載力，或根據梁的靜態承載力和沖擊能量來預估殘余變形。

2.3.2 彎剪破壞

由圖4可知，配筋率為1.00%和2.01%的試件發生彎剪破壞。如圖13(b)，假定剪切破壞時R-δ曲線為平行四邊形，曲線面積為試件彎剪破壞時的耗能(Eks)

Eks=δmax(Rmax-R0)

(7)

式中：δmax為跨中位移最大值；R0為最大位移時刻對應的支反力。對彎剪破壞型試件(ρ=1.00%和ρ=2.01%)的支反力最大值Rmax和跨中位移達到峰值時刻的支反力R0進行整理，如圖14所示。試驗結果表明R0隨Rmax的提高呈線性增長，擬合后得

R0=0.74Rmax-2.07

(8)

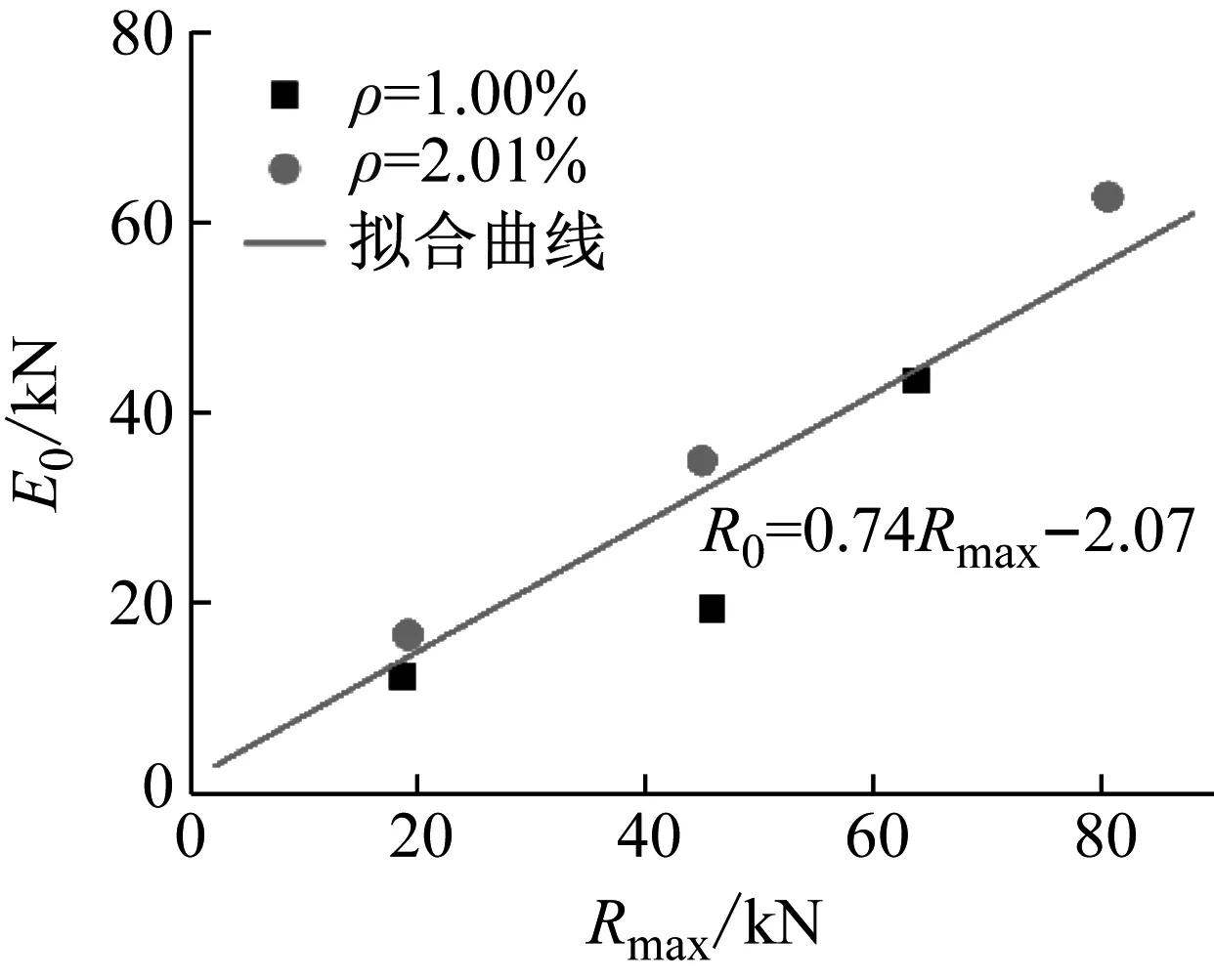
圖14 彎剪破壞模式下R0與Rmax的關系Fig.14 The relation between R0 and Rmax for bending-shear failure

聯立式(7)和(8)后得

Eks=δmax(0.26Rmax+2.07)

(9)

利用式(9)得到不同沖擊速度下試件發生彎剪破壞時的耗能。與試驗結果對比后發現計算值比試驗值分別增大了20.11%、1.6%、26.11%(ρ=1.00%)；28.61%、29.1%、7.73%(ρ=2.01%)。將式(3)和(9)代入到式(2)中可得

(10)

整理后得

(11)

利用式(11)，可以推導一定沖擊能量下鋼筋混凝土缺口梁發生彎剪破壞時所需的靜態抗剪承載力，或根據梁的靜態承載力和沖擊能量來預估梁的最大變形。

3 結 論

本文對不同配筋率的鋼筋混凝土缺口梁進行沖擊速度為9.89×102mm/s、1.71×103mm/s和2.21×103mm/s的落錘沖擊三點彎試驗，通過對比分析沖擊力、支反力、跨中位移和裂紋擴展形態，探討了沖擊速度和配筋率對鋼筋混凝土梁破壞模式和承載性能的影響。主要結論如下：

(1) 配筋率低于0.50%時鋼筋混凝土缺口梁發生彎曲破壞，一條主裂紋從預制缺口根部處起裂并擴展至加載點附近；反之，試件發生彎剪破壞，且隨著沖擊速度的增大，加載點下方裂紋擴展受到明顯抑制，試件表面產生斜裂紋。

(2) 不同沖擊速度下鋼筋混凝土缺口梁發生彎曲/彎剪破壞時，均可采用支反力峰值以評估梁的承載性能；支反力峰值和靜態抗彎/抗剪承載力的比值與沖擊速度呈線性增長關系，基于該擬合公式可預估一定沖擊速度范圍內鋼筋混凝土缺口梁發生彎曲/彎剪破壞時的承載力。

(3) 沖擊速度小于2.21 m/s時，鋼筋混凝土缺口梁發生彎曲/彎剪破壞的支反力-跨中位移曲線可以簡化為不同的平行四邊形以評估試件整體破壞消耗的能量。

(4) 假定梁吸收能量與沖擊能量的比值為0.25時，靜態抗彎/抗剪承載力關于沖擊速度和梁跨中位移的經驗公式可預估一定沖擊能量下不同破壞模式鋼筋混凝土缺口梁的變形，為沖擊荷載下鋼筋混凝土梁的安全評估提供一定參考。