基于改進經驗包絡法的非線性系統參數識別

曾 華， 許福友

(大連理工大學 建設工程學部， 遼寧 大連 116024)

模態參數(包括模態頻率、模態阻尼等)是土木(工程結構系統的重要參數，通常通過結構動力試驗(包括強迫振動、自由振動和環境激勵下的隨機振動)獲得的振動(位移或加速度)信號來識別。由于大型復雜土木工程結構的強迫振動試驗，對激勵設備和能量要求較高，且過大的強迫激勵會對結構安全與運營造成，難以開展強迫振動試驗，因此常采用無需對輸入進行測量的自由振動試驗或環境激勵下的隨機振動試驗，這種只對輸出進行測量的模態識別一般被稱作基于輸出的模態參數識別(output-only modal analysis, OMA)方法。

OMA方法一般可分為時域分析法、頻域分析法和時頻分析法三類。其中，時域分析方法是對結構振動時程響應直接分析，如隨機減量技術(random decrement technique, RDT)[1]，隨機子空間法(stochastic subspace identification, SSI)[2]等；頻域分析方法一般通過傅里葉變換到頻域再進行模態參數識別，主要有峰值拾取法[3]，頻域分解法[4-5]等；時頻分析法一般有基于小波變換(wavelet transform, WT)[6]、基于希爾伯特變換(Hilbert transform, HT)[7-8]、基于經驗分解(empirical mode decomposition, EMD)[9-10]、基于極點對稱模態分解(extreme-point symmetric mode decomposition, ESMD)[11]、基于變分模態分解法(variational mode decomposition, VMD)[12-15]等信號分析方法。其中，WT方法受母小波選擇的影響，人為因素較大，沒有通用的小波函數。EMD方法是一種自適應的信號分解技術，它與HT方法結合成為一種強大的時頻分析技術，通常被稱為希爾伯特-黃變換(Hilbert-Huang transform, HHT)[16]，廣泛運用于機械土木等領域，并有不錯識別的效果。王金良等在HHT基礎上提出一種自適應分解的ESMD法，該方法通過極點對稱構造內部的局部對稱均線，能夠降低插值帶來的不確定性，但同樣存在模態混疊問題。VMD方法是通過迭代搜索變分模型最優解來獲取每個分量的中心頻率與帶寬，克服了EMD方法的模態混疊等缺陷，并已應用在非線性系統模態參數識別及非平穩信號分析等問題中。

對于土木結構的振動系統，其模態參數往往表現為非線性函數。其中瞬時頻率和瞬時阻尼比是非線性系統最為關注的模態參數。求解信號瞬時特性的常見方法有：相位差法，能量算子法，小波變換法，Hilbert變換法(HT)以及經驗包絡法。張賢達[17]提出相位差分法，對線性系統具有無偏估計、零延遲等優點，但對噪音過于敏感。Maragos等[18]利用能量算子將單分量信號分離為調幅和調頻分量，并總結了幾種有效的瞬時頻率估計方法，具有原理簡單、計算量小等優點，廣泛應用[19]。但能量算子法基于線性相位假設，因此應用于非線性系統時將會產生很大誤差。Staszewski[20]運用系統響應首先分解得到時程小波脊和小波骨架，然后求解信號的時程瞬時特性，最后識別非線性系統參數，具有較好的精度。Feldman[21-22]詳細論述了HT在非線性系統識別中的應用，該方法會產生明顯端點效應、負頻率等現象。

鄭近德等[23]基于經驗調幅調頻分解，提出了經驗包絡法(empirical envelope, EE)，并驗證了EE在求解瞬時頻率具有計算量小，識別精度高，操作簡單等優點。不過，在整個求解過程中存在兩點不足：① 調幅調頻分解中，為了得到較純的調頻信號，需要多次包絡迭代，這樣將會導致樣條插值的累計誤差的增大；② 對信號求導時，由于信號不光滑，可能造成過包絡問題，即包絡線與信號線相交，導致包絡誤差增加。因而，EE用于信噪比較小的非線性結構信號時，常出現識別結果不穩定現象。

針對上述兩個問題，本文采用滑窗閾值去噪思想與滑動平均技術對其改進，提出了改進的經驗包絡法(improved empirical envelope, IEE)。通過多種信號參數識別與分析，全面證實了該方法利用自由振動試驗識別模態參數的有效性。

1 經驗調幅調頻分解

任意單頻信號y(t)均可分解為調幅函數和調頻函數的乘積形式，即：

y(t)=a(t)cos(φ(t))

(1)

式中：a(t)為調幅函數；cos(φ(t))為調頻函數；φ(t)為瞬時相位。

經驗調幅調頻分解具體過程如下

步驟1對y(t)取絕對值|y(t)|，搜尋|y(t)|的所有極值點(ti,|yi|)(i=1,2…,N)，i為極值點編號，N為極值點的個數

步驟2采用三次樣條擬合這些極值點(ti,|yi|)，得到|y(t)|的第一輪經驗包絡函數曲線a1(t)

步驟3對|y(t)|歸一化為

y1(t)=|y(t)|/|a1(t)|

(2)

理想條件下，y1(t)應小于等于1。由于y(t)可能存在明顯的噪聲甚至野點，因此并不能保證在任何時刻a1(t)>|y(t)|，即某些時刻y1(t)有可能大于1。此時，將y1(t)視為y(t)，重復步驟1～2，經n次迭代

y2(t)=y1(t)/|a2(t)|

(3)

……

yn(t)=yn-1(t)/|an(t)|

(4)

直到yn(t)≤1，迭代結束，此時的yn(t)為y(t)調頻部分。存在φ(t)，使得：

yn(t)=cos(φ(t))

(5)

y(t)調幅部分可定義為

(6)

至此，原信號y(t)可以分解為調幅調頻兩部分乘積a(t)cos(φ(t))形式。

以上經驗調幅調頻分解至少存在兩方面不足：

(1) 由于噪聲的存在，為了得到純調頻信號，需要多輪包絡迭代，這樣將會導致樣條插值的累計誤差增大。

(2) 三次樣條插值存在端點效應。

下節將針對這兩方面的不足進行改進，提高分解精度。

2 調幅調頻分解的改進

2.1 包絡迭代的改進

采用滑窗閾值去噪思想篩選剔除異常極值點。具體步驟如下：

步驟1搜尋|y(t)|的所有極值點，并確定其極值點(ti,|yi|)(i=1,2…,N)，i為極值點編號，N為極值點的個數

步驟2對|y(t)|極值點集U={(ti,|yi|)}(i=1,2,…,N)，按“窗體”極值點個數為W1進行滑動，并選取第1個子集Q1={(tj,|yj|)}(j=1,2,…,W1)

步驟3對子集Q1進行最小二乘法擬合

(7)

擬合優度定義為

(8)

步驟4搜索子集Q1內所有異常極值點

η<ηc

(9)

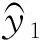
步驟5“窗體”向前滑動一個極值點，選取得到子集第2個Q2={(tj,|yj|)}(j=2,3,…,W1+1)，按同樣方法搜尋異常極值點集合ERR2

步驟6“窗體”繼續滑動，直至選取最后一個子集QN-W1+1={(tj,|yj|)}(j=N-W1+1,N-W1+2,…,N)，并搜尋異常極值點集合ERRN-W1+1

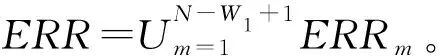
后續過程與調幅調頻分解相同，此處不再贅述。需要說明的是，“窗體”大小W1和閾值因子ηc應該選擇適當，過大過小都會影響最后結果。“窗體”(閾值因子)過大將會舍去大量的極值點，出現欠包絡現象，從而導致調幅調頻信號的失真；“窗體”(閾值因子)過小會導致極值點篩選不充分，出現過包絡現象，從而導致調幅調頻信號不穩定。一般而言，對于信噪比較小、質量較差的信號，可適當增加W1與ηc的值；對于信噪比較大、質量較好的信號，可適當減小W1與ηc的值。通過對大量理論模擬信號分析可知，“窗體”大小可以在(8～20)范圍內取值，閾值因子可在(0.3～0.9)范圍內取值。在此范圍內，W1與ηc的選取對結果影響較小。

2.2 端點效應的改進

本文采取極值點向外線性延伸手段，來抑制端點效應，具體步驟如下：

步驟1取待擬合的極值點的前兩個極值點(t1,|y1|)與(t2,|y2|)；

步驟2令Δ=(|y1|-|y2|)/(t1-t2)，計算Δy=|y1|-t1Δ；

步驟3如果Δy>|y(0)|，則首部向外延伸點為(0，Δy)，否則為(0，|y(0)|)；

步驟4尾部向外延伸點可按類似方法計算，此處不再贅述。

3 經驗包絡法

獲得調幅調頻函數后，對調頻函數求導可以獲得新函數，然后再對該新函數進行經驗調幅調頻分解，最終獲得原始信號y(t)的瞬時頻率與瞬時振幅。具體步驟如下：

步驟1對F(t)=cos(φ(t))求導可得F′(t)=-φ′(t)sin(φ(t))，y(t)的瞬時頻率f(t)可表示為

(10)

步驟2再對-φ′(t)sin(φ(t))進行調幅調頻分解可得

F′(t)=b(t)cos(φ(t))

(11)

式中，b(t)可看作φ′(t)。因此原信號的瞬時頻率為

(12)

經驗包絡法相對小波變換法、Hilbert變換法有計算量小，識別精度高，操作簡單等優點[24]。但仍存在問題：對信號求導，如果信號不光滑，可能造成過包絡問題，即包絡線與信號線相交，導致包絡誤差增加。

4 經驗包絡法的改進

本文采用滑動平均算法對經驗包絡法步驟2中調幅調頻分解求導后的信號F′(t)進行滑動平均處理，去除因求導之后信號混有不光滑的成分。具體操作步驟如下：

步驟1將F′(t)看作采樣信號S(t)；

步驟2選取固定長度為W2的采樣數據隊列；

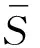
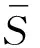
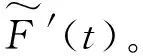
需說明的是，應選取合適的W2，其值越大平滑效果越好，識別結果越穩定，但過大會導致信號失真。一般而言，對于采樣頻率較高、信噪比較小、質量較差的信號，可適當增加W2的值；采樣頻率較低、信噪比較大、質量較好的信號，可適當減小W2的值。通過對大量理論模擬信號分析可知，W2可在(2～20)內取值。

為了說明對調幅調頻分解與經驗包絡法改進后的效果，現給出示意圖加以說明。如圖1所示，給出了異常極值點分別采用調幅調頻分解與改進調頻調幅分解得到的包絡誤差影響的示意圖。由圖1可知，通過對異常極值點的剔除，避免了過包絡現象，減小了包絡誤差，進而減少了包絡迭代次數。圖2給出了求導后信號不光滑性對包絡誤差的影響的示意圖。由圖2可知，通過對求導后信號的滑動平均處理，可以有效的減小包絡誤差。

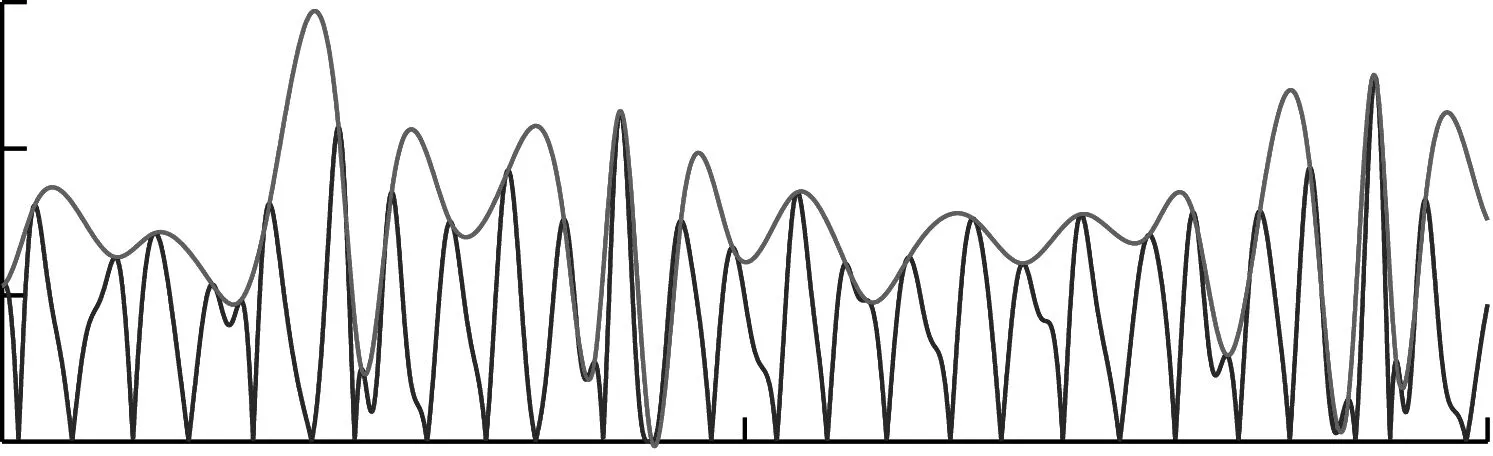
(a) 調頻調幅包絡

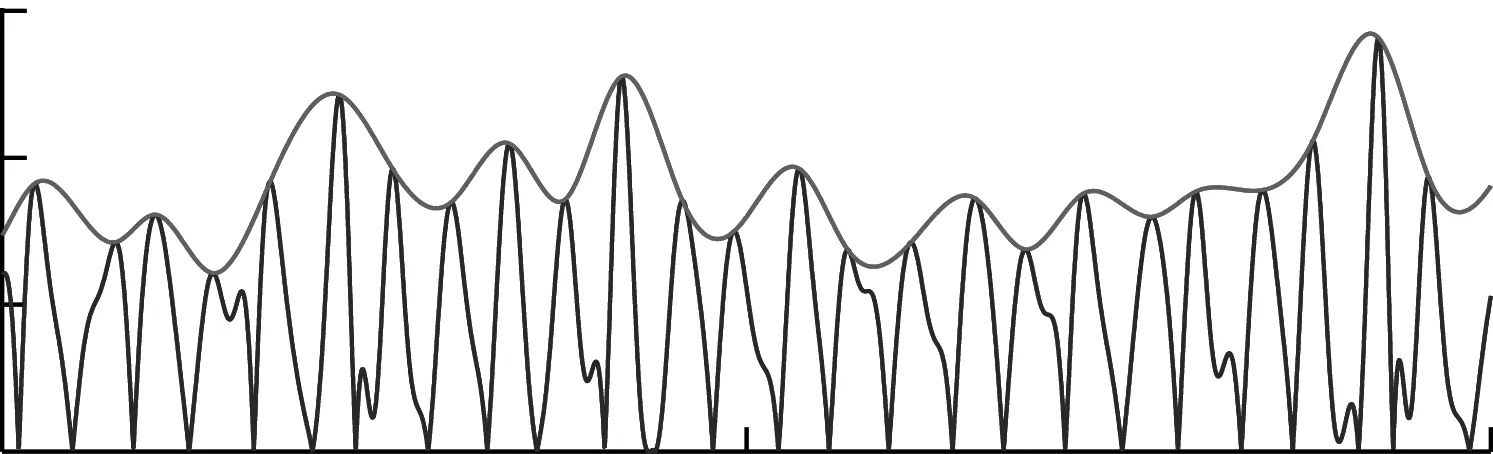
(b) 改進調幅調頻包絡圖1 異常極值點對包絡影響示意圖Fig.1 Schematic diagram of influence of abnormal extreme point on envelope

(a) EE包絡

(b) IEE包絡圖2 求導信號不光滑對包絡插值影響示意圖Fig.2 Schematic diagram of influence of unsmooth derivative signal on envelope difference

5 模態參數識別

由單分量自由衰減信號的瞬時振幅a(t)可導出阻尼系數為

(13)

式中，m為離散采樣極值點。故單分量自由衰減信號的瞬時阻尼比ξ(t)可以表示為

(14)

在低阻尼下，單分量自由衰減信號的瞬時阻尼比可近似計算為

(15)

如圖3所示，為絕對誤差ξr隨阻尼比的變化。其中ξr可按下式給出

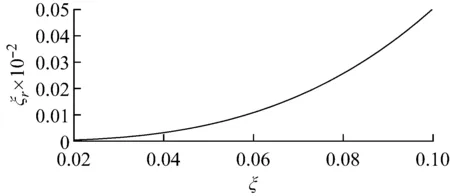
圖3 阻尼比的誤差Fig.3 Relative error of damping ratio

ξr=ξ′-ξ

(16)

式中，ξ為精確結果由式(14)算出，ξ′為近似結果由式(15)算出。

由圖3可知，當ξ<0.1時，通過式(15)計算，ξr低于0.000 5，因此單分量自由衰減信號在低阻尼情下，采用式(15)是合理并且方便的。

這里需要說明的是，式(13)～(15)僅適用于單分量自由衰減振動，故而本文提出的非線性系統模態參數識別的方法也僅適用于單分量自由衰減振動。但本文方法可以與VMD、EMD、ESMD、RDT等方法結合，形成一種比較通用的非線性系統識別方法。例如，對于單模態自由振動，可直接利用本文方法識別時變模態參數；對于多模態自由振動，可以現利用帶通濾波器(如若存在密集模態問題，該方法欠佳)或者VMD等分解技術將多模態解耦，再利用本文方法識別時變模態參數；對于多模態環境激勵[25]，可先通過功率譜分析確定合適的帶寬，使用帶通濾波器將其分解為多個窄帶信號，再對這些窄帶信號使用VMD等技術進行解耦，并利用RDT技術將其轉化為單分量自由衰減信號，最后利用本文提出的方法識別時變模態參數。下文通過幾個算例進一步說明。

6 算 例

本節采用三個算例對比驗證EE與IEE識別效果，下文均為端點效應處理后的識別結果。

6.1 算例一

某單自由度非線性系統阻尼比ξ=0.005+0.001A，圓頻率為ω=2π(2-0.01A)，其中A(0.5≤A≤5)為振幅，采樣頻率為500 Hz，初始振幅A0=5 cm，通過Newmark-β法可計算非線性系統的自由衰減振動響應。

對系統響應施加信噪比為80 dB零均值的高斯白噪聲n，如圖4所示。對于信噪比可表示為

SNR=10lg(Ps/Pn)

(17)

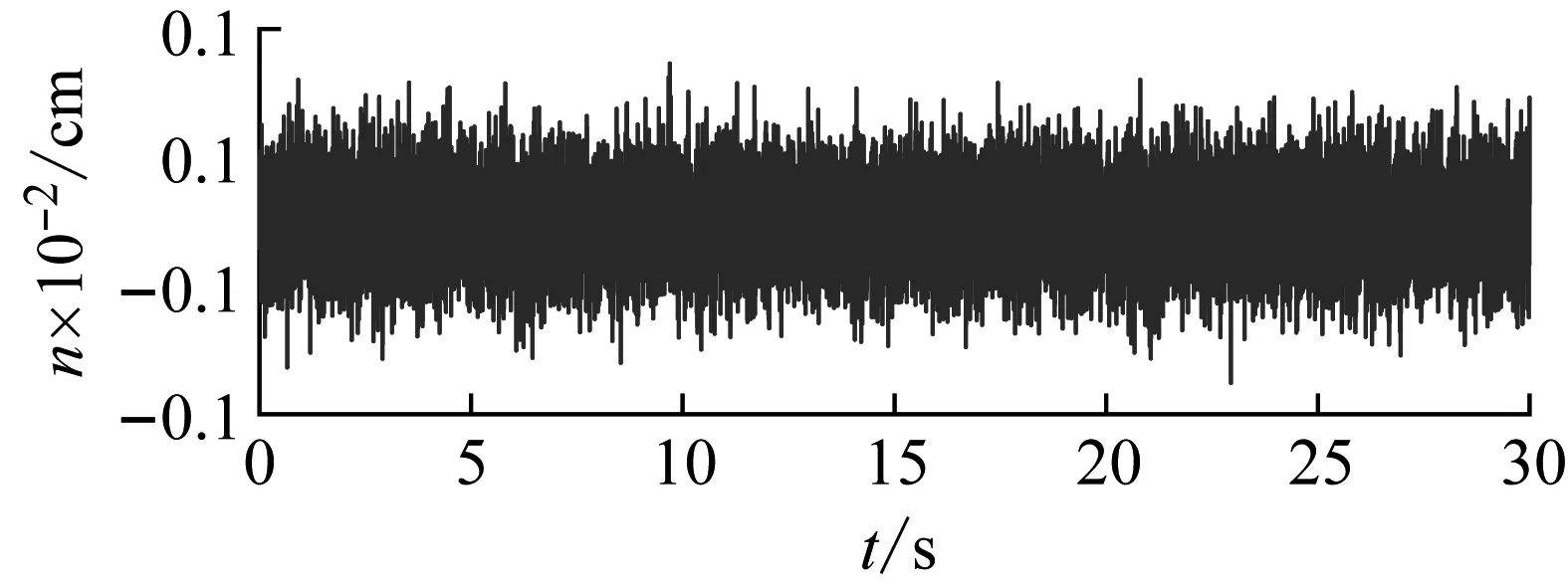
圖4 高斯白噪聲Fig.4 White Gaussian noise

式中：Ps為信號的平均功率；Pn為噪聲的平均功率。添加噪聲后的模擬信號如圖5所示。

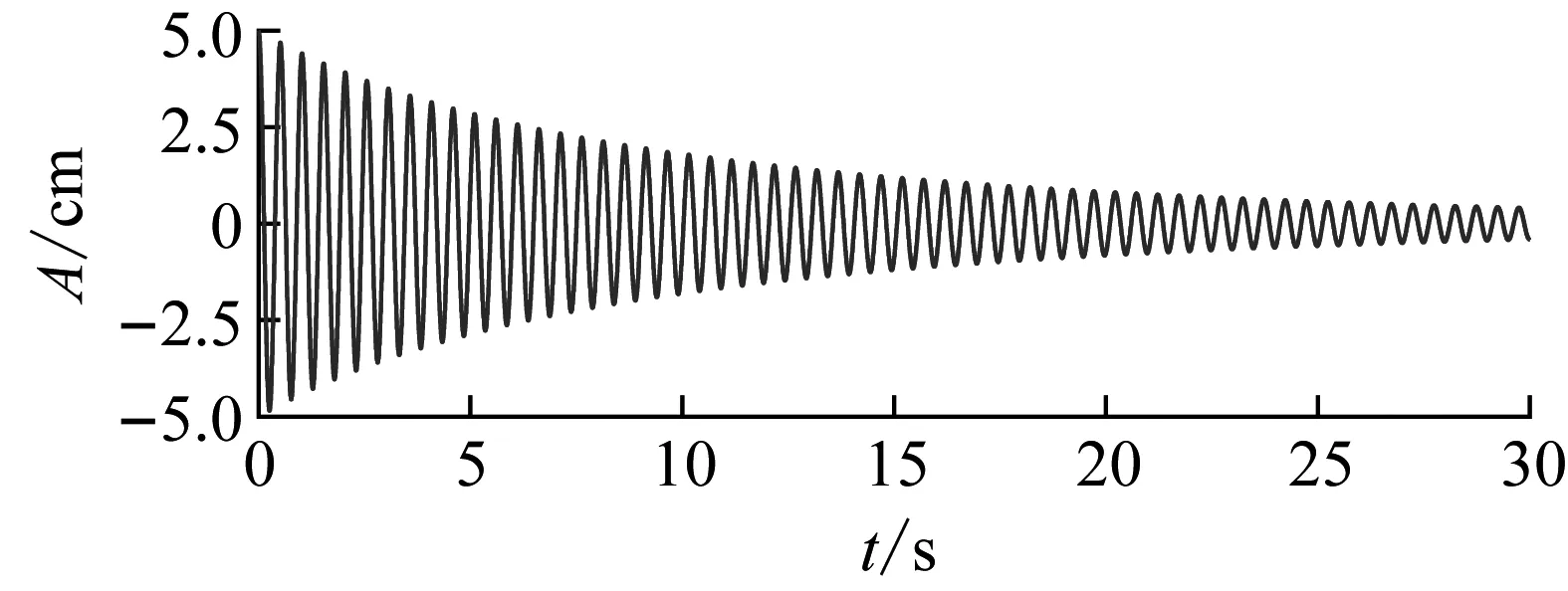
圖5 模擬信號Fig.5 Analog signal

對信號A(t)(為保證識別的準確性，截去信號的前三個波峰)分別采用EE與IEE(W1=14,W2=4，ηc=0.5)識別計算，可得瞬時頻率與瞬時阻尼比，分別如圖6和圖7所示。由圖6(a)可知，EE識別的瞬時頻率波動范圍較大，且在小振幅區間偏離真值。這是由于噪聲對小振幅區域信號影響更加明顯，導致小振幅區間出現大量異常極值點，進而在經驗調幅調頻分解時，出現過包絡現象既增加了三次樣條擬合誤差，又增加了包絡迭代次數，最終導致小振幅處識別結果偏差很大，甚至錯誤。由圖6(b)所示，IEE識別的瞬時頻率波動范圍較小，識別結果更穩定。

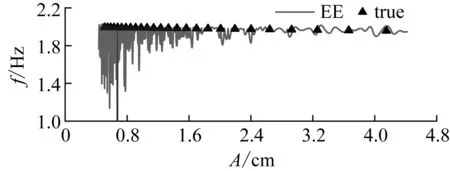
(a) EE識別結果

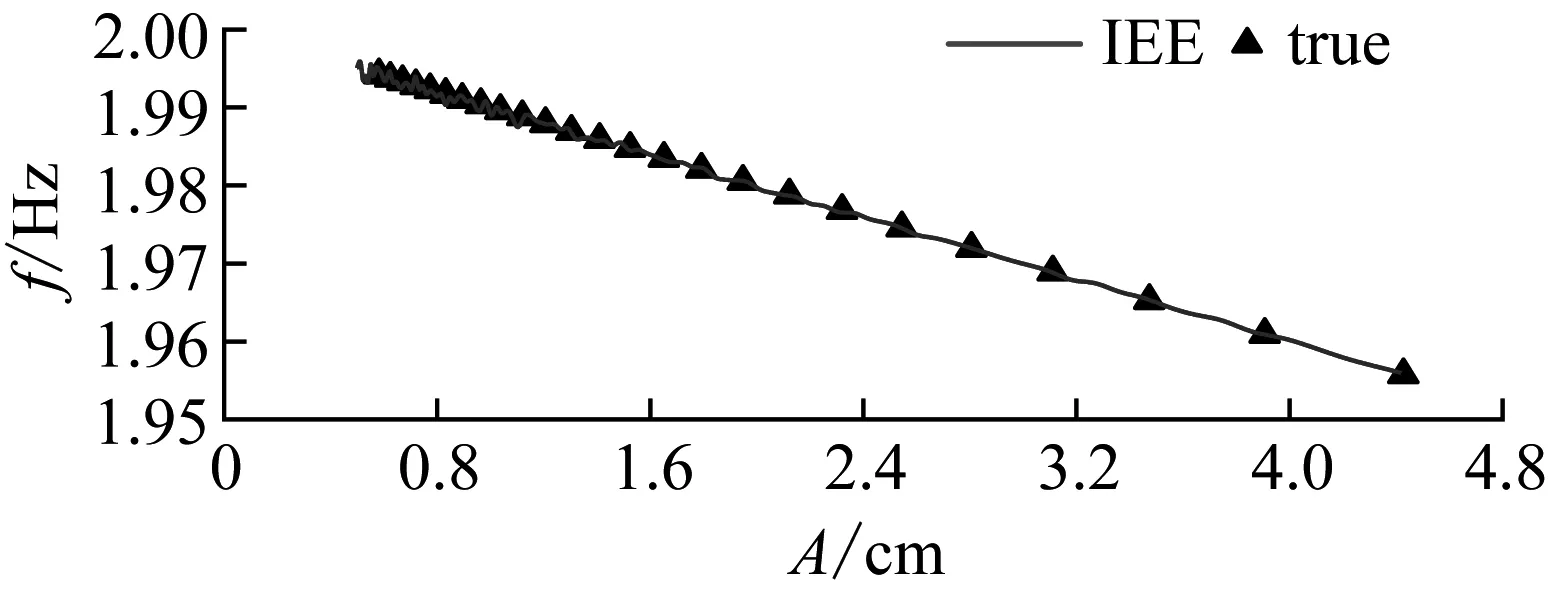
(b) IEE識別結果圖6 幅變頻率Fig.6 Variable instantaneous frequency

如圖7(a)所示，由于EE識別的瞬時頻率在小振幅處有異常波動，直接影響了瞬時阻尼比的識別結果，導致其結果在小振幅處偏離真值。如圖7(b)所示，IEE識別的瞬時阻尼比非常穩定，其相對優勢顯而易見。

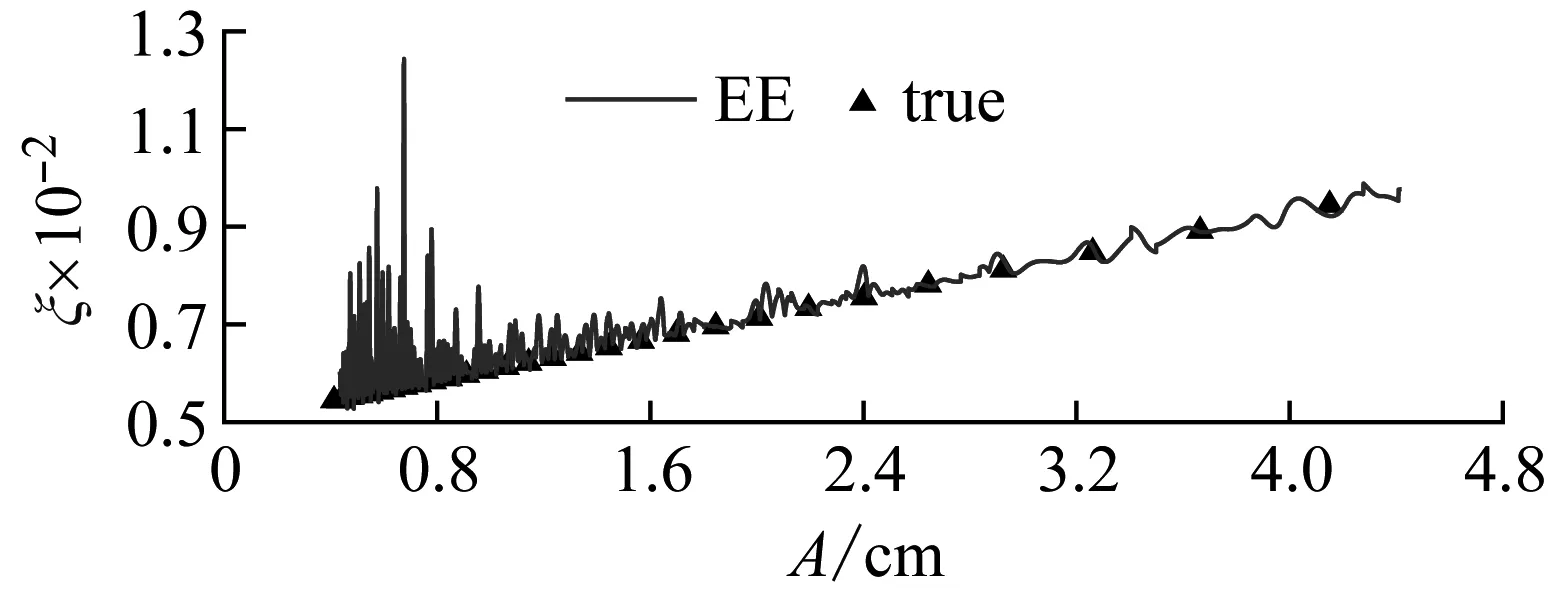
(a) EE識別

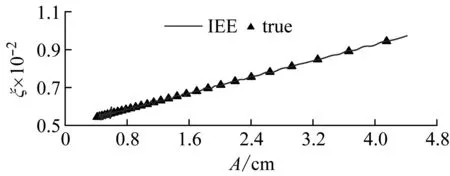
(b) IEE識別圖7 幅變阻尼比Fig.7 Variable instantaneous damping ratio

為了進一步說明噪聲強度與噪聲均值對識別結果的影響。現對模擬信號施加不同信噪比，瞬時頻率識別誤差如表1所示。施加不同均值的噪聲，瞬時頻率識別誤差如表2所示。

表1 均值為零不同信噪比瞬時頻率識別結果Tab.1 Recognition results of instantaneous frequency with zero mean value and different SNR

表2 SNR為80不同均值瞬時頻率識識別結果Tab.2 Recognition results of instantaneous frequency with SNR of 80

瞬時頻率識別誤差R按下式給出

R=|f′-f|/f×100%

(18)

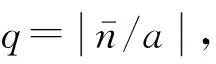
“窗體”大小W1和閾值因子ηc對信號A(t) 頻率識別誤差如表3、表4所示。

表3 不同“窗體”大小IEE識別頻率誤差Tab.3 Frequency error identification by IEE with different sliding window width

表4 不同閾值因子IEE識別頻率誤差Tab.4 Frequency error identification by IEE with different threshold factors

由表3和4可知，“窗體”大小與閾值因子對識別結果影響較小，因此，本文推薦取值范圍是合理的。

6.2 算例二

本信號為單自由度沒水圓柱縱搖自由衰減振動角位移時程，如圖8所示。

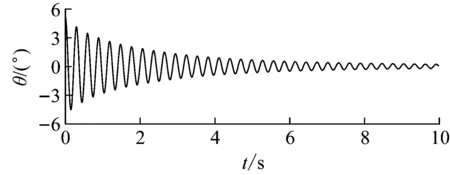
圖8 數值模擬信號Fig.8 Numerical simulation signal

對數值模擬信號分別采用EE與IEE(W1=10,W2=8,ηc=0.8)識別計算，可得瞬時頻率和瞬時阻尼比。如圖9所示，EE識別的瞬時頻率出現較大的波動，導致識別結果不可用。這是因為數值誤差的影響，對信號求導時，出現過包絡現象，即包絡線與信號線相交(見圖2(b))，導致包絡迭代進入死循環。而IEE識別的瞬時頻率無任何異常，識別效果很好。

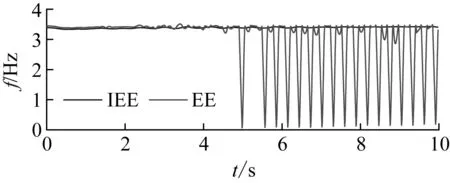
圖9 瞬時頻率Fig.9 Instantaneous frequency

如圖10所示，為兩種方法識別幅變瞬時阻尼比。圖10(a)為擺角大于1°的識別結果，由于EE識別的瞬時頻率波動的影響，導致EE識別阻尼比結果波動較大；IEE識別結果隨擺角逐漸增大，結果較為穩定。圖10(b)，為擺角小于1°EE的識別結果，由于EE識別的瞬時頻率在小擺角區間異常，導致阻尼比識別結果不可用。圖10(c)，為擺角小于1°IEE的識別結果，可以看出IEE在小擺角區間識別效果也較好。

6.3 算例三

為說明本文方法能應用于實際結構當中，現以蘇通大橋為背景建設的自然風場大比例試驗模型[26]為研究對象，試驗模型效果圖如圖11所示。主梁斷面布置22個加速度傳感器，分別為AL-1～AL-11(主梁左側)、AR-1～AR-11(主梁右側)如圖12所示。

圖11 試驗模型效果圖Fig.11 Effect diagram of test model

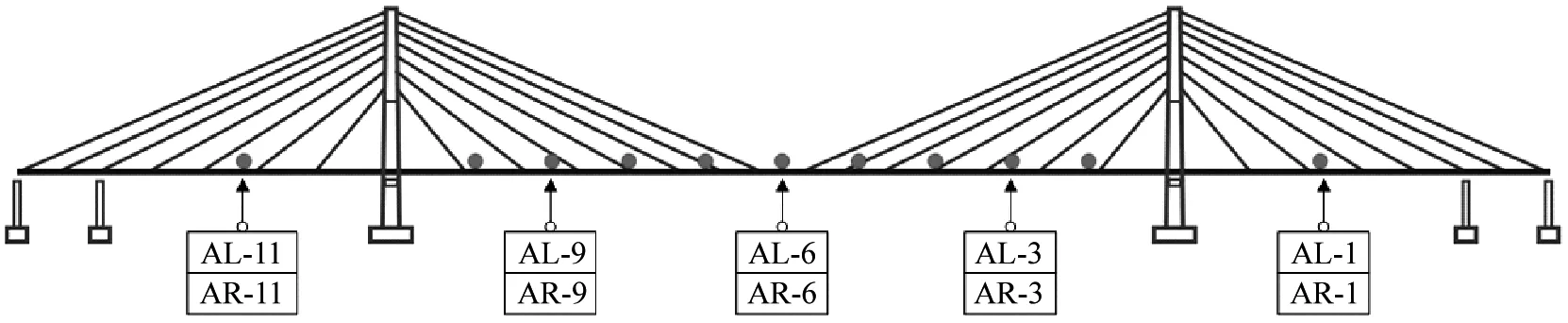
圖12 傳感器布置示意圖Fig.12 Schematic diagram of sensor arrangement

6.3.1 廣義單自由度自由衰減振動

為了獲取模型一階對稱豎向振動模態參數，在無風環境下，對主梁跨中施加初始位移使其作自由衰減振動，以跨中AL-6加速度(采樣頻率為400 Hz)響應為例，如圖13所示。

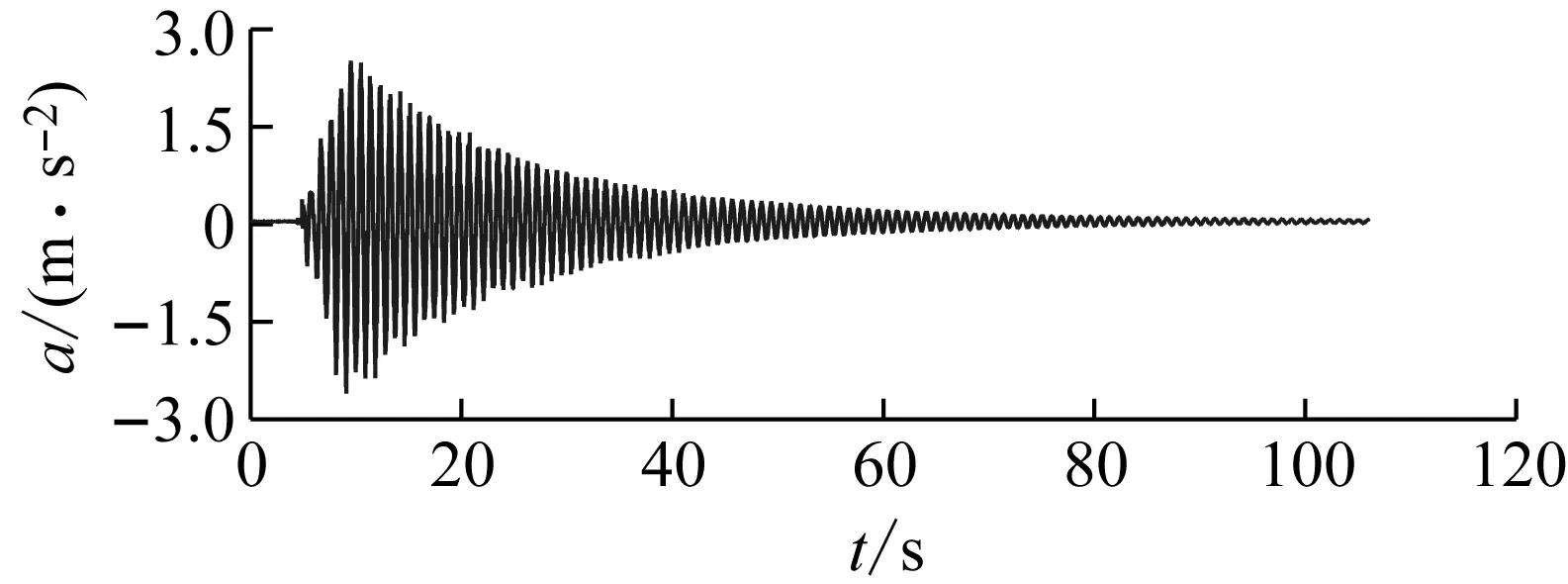
圖13 AL-6加速度響應Fig.13 AL-6 acceleration response

為保證識別的精度，現對該信號采用低通濾波器(截止頻率為2 Hz)濾波處理，并截去前10 s與后15 s響應。如圖14所示。

圖14 濾波后加速度信號Fig.14 Filtered acceleration signal

現對濾波后信號分別采用EE與IEE(W1=10,W2=10,ηc=0.8)識別計算，可得瞬時頻率與瞬時阻尼比。圖15(a)為t< 64 s兩種方法識別瞬時頻率的結果，可以看出兩種方法識別結構較為接近。圖15(b)為t> 64 s EE識別瞬時頻率的結果，可以看出識別結果出現大幅波動。這是因為濾波后殘余噪聲以及信號非平穩等因素的影響，對信號求導時，出現過包絡現象，即包絡線與信號線相交(如圖2(b)所示)，導致包絡迭代進入死循環。圖15(c)為t> 64 s IEE識別瞬時頻率的結果，可以看出識別結果較為穩定。

圖16(a)為a> 0.2 m/s2兩種方法識別幅變阻尼比的結果，可以看出兩種方法識別結構較為接近。圖16(b)為a< 0.2 m/s2EE識別幅變阻尼比的結果，由于EE識別的瞬時頻率波動的影響，導致識別結果不可用。圖16(c)為a< 0.2 m/s2IEE識別幅變阻尼比的結果，可以看出識別結果較為穩定。

為了進一步說明IEE的有效性，現將識別的模態頻率與模態阻尼比代入單自由度動運動微分方程，運用Newmark-β法計算結構位移響應。為了比較的精準性，只截取30 s信號加以對比分析，如圖17、圖18所示。由圖可知，通過IEE識別的模態參數反算結構位移響應更加接近真實的位移響應，驗證了IEE的有效性。

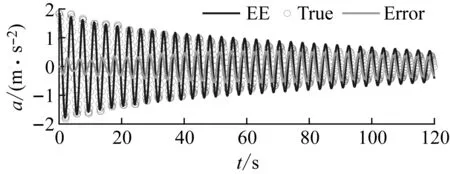
圖17 EE計算結構響應Fig.17 EE calculation of structural response

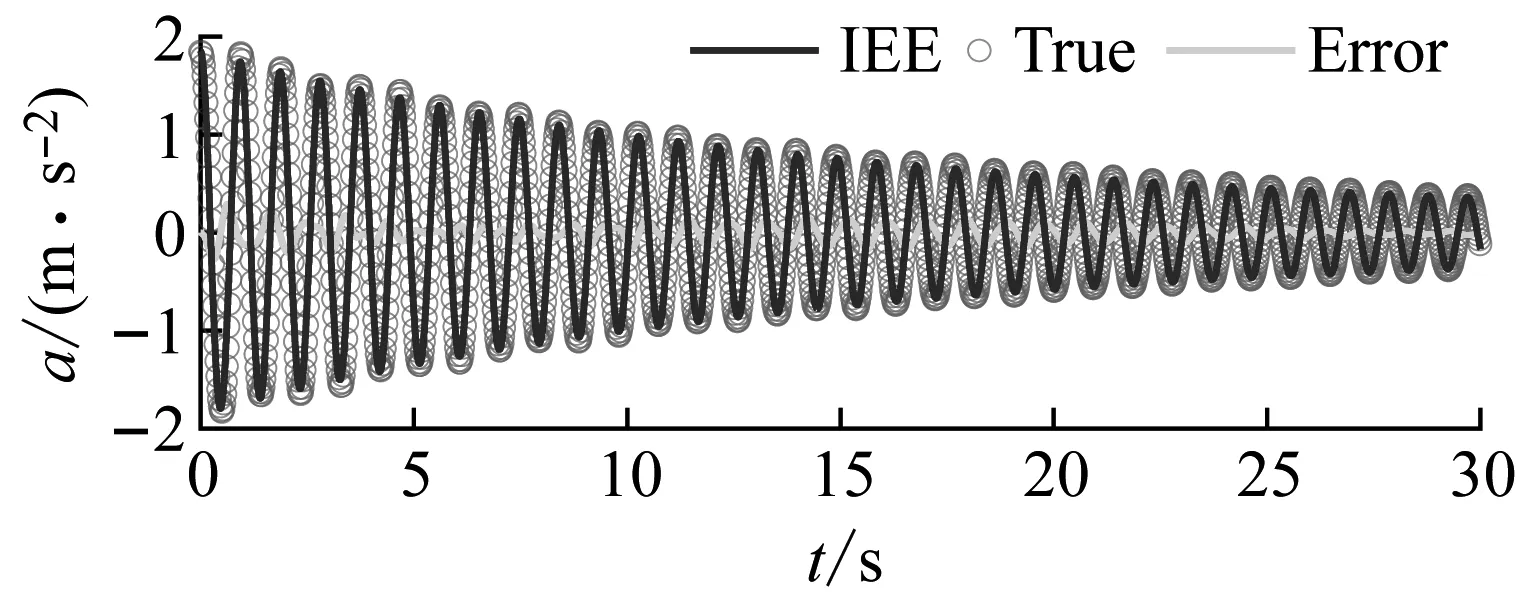
圖18 IEE計算結構響應Fig.18 IEE calculation of structural response

6.3.2 多自由度自由衰減振動

為了獲取模型高階豎向振動模態參數，在無風環境下，對主梁八分點施加初始位移使其作自由衰減振動，以AL-3加速度(采樣頻率為400 Hz)響應為例，如圖19所示。由圖可知，成功激勵出高階豎向振動模態。通過幅值譜分析(如圖20所示)，可初步判斷該信號存在兩階模態，其頻率大約在2.5 Hz與5 Hz左右。

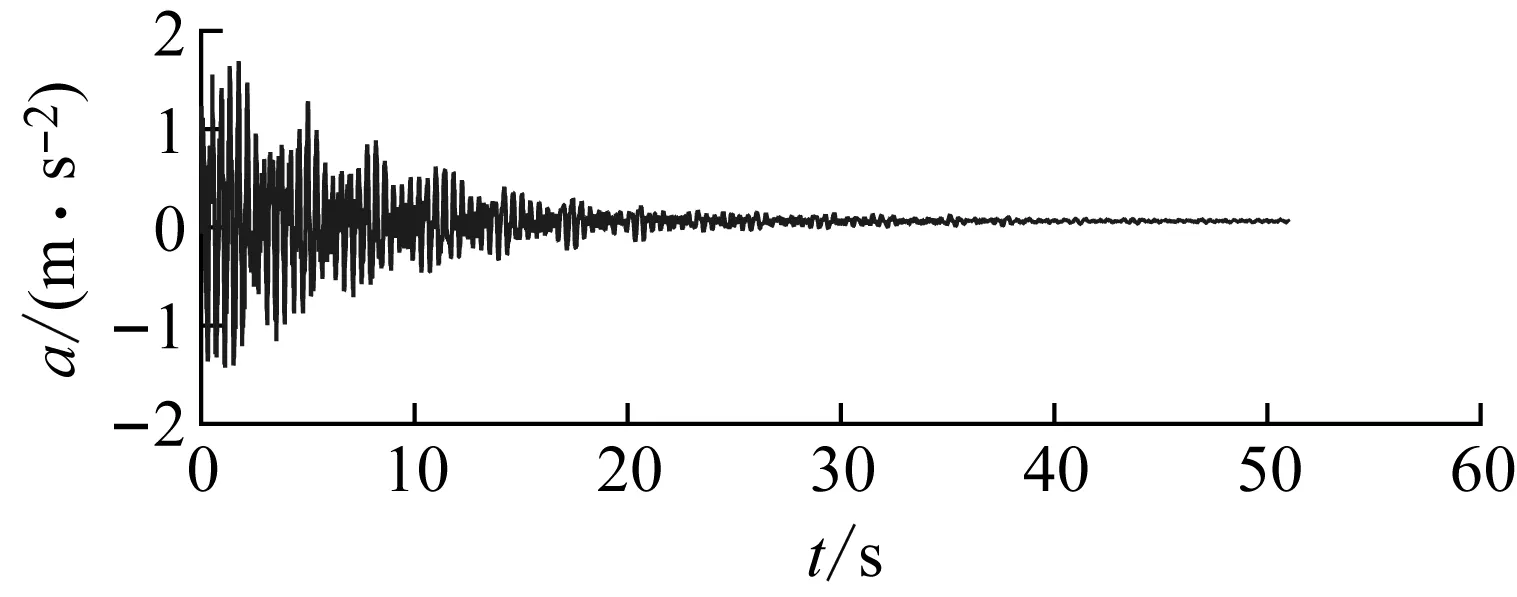
圖19 AL-3加速度響應Fig.19 AL-3 acceleration response

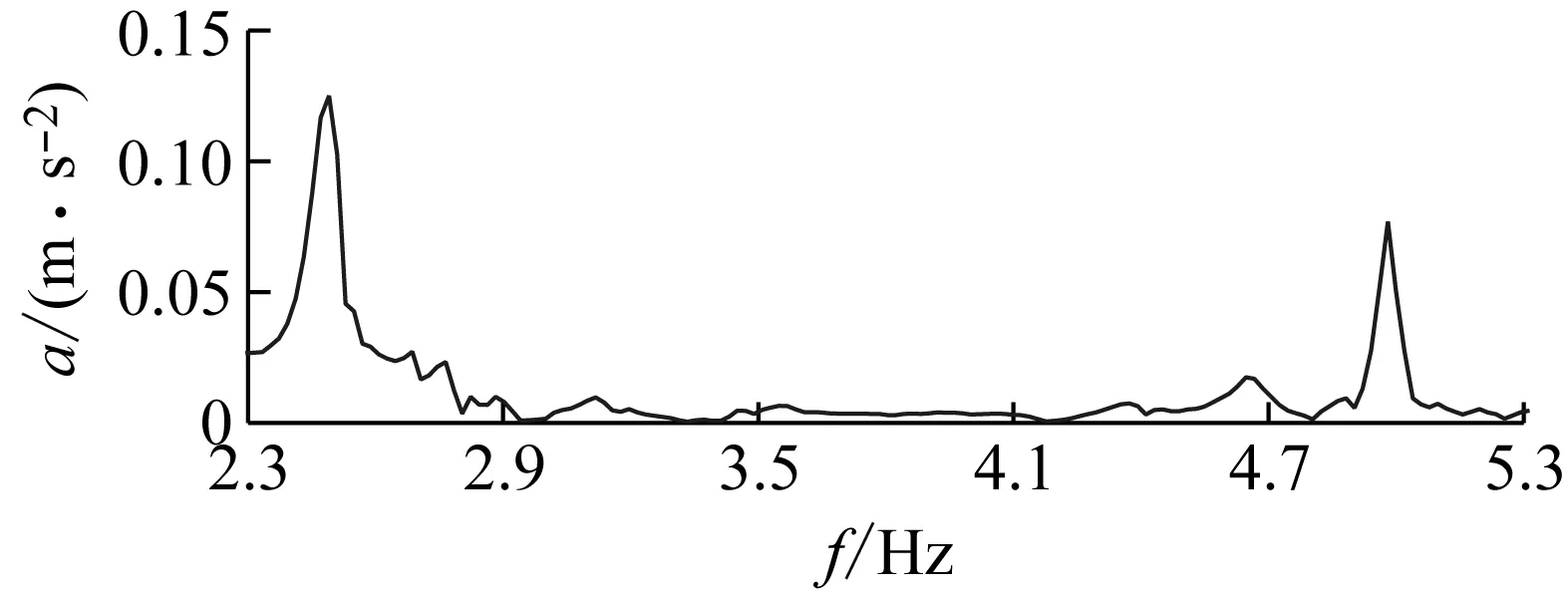
圖20 加速度響應幅值譜Fig.20 Acceleration response amplitude spectrum

為保證識別的精度，現對該信號采用帶通濾波器(通帶頻率為2 Hz、5.5 Hz)濾波處理，并截去前10 s與后15 s響應。如圖21所示。

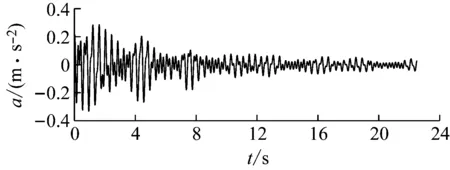
圖21 濾波后加速度信號Fig.21 Filtered acceleration signal

通過VMD法將該信號分解為兩個單模態響應(分別記為IMF1、IMF2，結果如圖22所示)，具體多模態參數分解過程，本文不重點展開討論，可參照文獻[27]。這里也可以使用帶通濾波器將兩個模態分解，但受帶通濾波器阻帶衰減率的影響，當兩個模態頻率較為接近時，難以用帶通濾波器將其分開。故而，VMD等技術在處理模態耦合問題中更加通用。

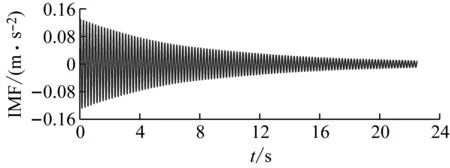
(a) IMF1模態

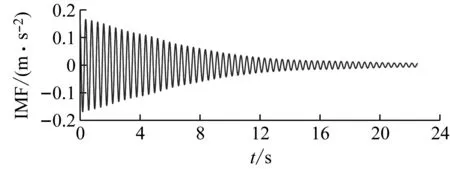
(b) IMF2模態圖22 單模態響應Fig.22 Single mode response

現采用IEE法分別對兩個單模態自由衰減信號進行識別計算，可得瞬時頻率與瞬時阻尼比。如圖23所示，成功識別出了兩階模態頻率。如圖24所示，成功識別出了兩階模態阻尼比，但對于IMF2識別的阻尼比波動較大，這是由于利用VMD重構信號時，部分信號振幅失真導致的。

圖23 瞬時頻率Fig.23 Instantaneous frequency

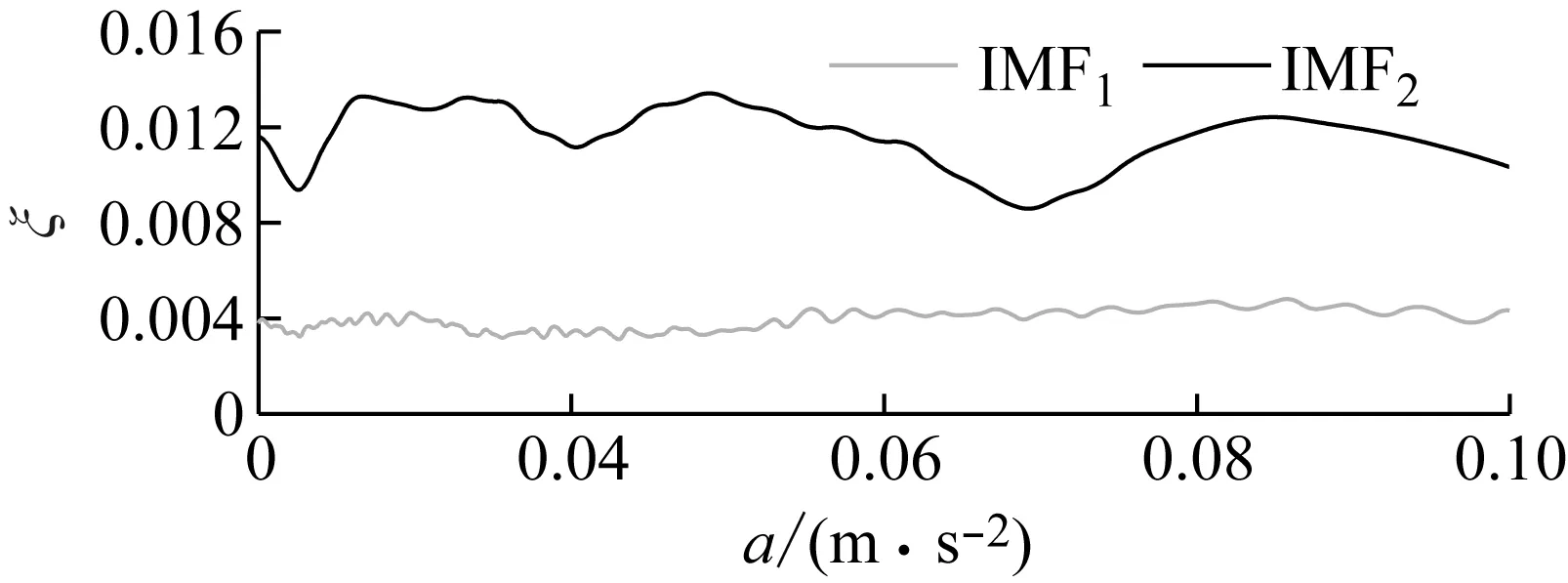
圖24 幅變阻尼比Fig.24 Amplitudevarying damping ratio

7 結 論

針對非線性系統瞬時頻率問題，提出了改進經驗包絡法，其關鍵技術包括：滑窗閾值去噪與滑動平均。基于該方法對單自由度(一般通過經驗模態分解、變分模態分解等方法解耦獲取)非線性系統自由衰減振動(一般通過自由振動試驗或通過隨機減量法從結構隨機振動響應中獲取)模態參數識別(瞬時頻率、瞬時阻尼)。通過幾個算例參數識別分析，證實了本文方法在利用自由振動試驗進行模態參數識別具有良好的抗噪聲性能與較高的識別精度。