基于改進度中心性的樣本點相似性度量方法

鄧 莉, 劉士虎

(云南民族大學 數學與計算機科學學院, 昆明 650504)

在現實生活中，許多諸如Facebook社交網絡[1]、蛋白質相互作用網絡[2-3]、航空網絡[4]、疾病傳播網絡[5]等都可以抽象為圖數據.圖數據不僅僅刻畫了樣本點的特征，還包含刻畫樣本點之間關聯情況的信息，即拓撲信息.鑒于圖數據在理論層面和市場需求具有的巨大應用價值，近年來其在各行各業掀起了研究高潮，并且取得了一系列卓有成效的研究成果[6-8].不難發現，圖數據中樣本點的相似性度量是一個重要的研究課題，在字符和圖形識別[9]、目標跟蹤[10]、城市交通網絡[11-12]等領域發揮著重要的作用.

隨機游走方法被廣泛用于度量樣本點的相似性，該方法無需圖數據的全局信息，衡量從特定樣本點出發，通過多步隨機游走到達另一個樣本點的過程.為了更好地使用此方法度量樣本點的相似性，研究者們相繼提出了多種隨機游走模型：如有偏的隨機游走模型(biased random walk，BRW)[13-14]，最大熵隨機游走模型(maximal entropy random walk，MERW)[15]，局部隨機游走模型(local random walk，LRW)[16]等.不足的是，這些隨機游走模型的樣本點相似性度量方法存在大度樣本點依賴問題.同時，這些方法從拓撲信息出發來度量樣本點基于結構的相似性，使其難以廣泛運用于度量屬性圖數據中樣本點相似性.文獻[17]針對屬性圖數據樣本點相似性的度量問題，提出了一種樣本點基于隨機游走的相似性度量方法:LLRWSMM-PCO.該方法充分討論了任意兩個樣本點關于拓撲結構的可達性，在樣本點可達的基礎上，度量樣本點基于拓撲信息的相似性，從而得到一種綜合的相似性度量方法.不足的是，該方法只針對無權無向圖數據.

除了基于隨機游走的樣本點相似性方法，大量的研究從樣本點共享鄰居的角度對樣本點相似性進行了研究[18-23].Salton[21]和Jaccard[22]分別提出了基于余弦距離和共享鄰居Jaccard指標，該指標認為樣本點的共享鄰居越多，其相似性程度越高.在文獻[23]中，Lada等從共享鄰居度的角度，提出了Adamic-Adar指標，該指標認為，共享鄰居的度越小，樣本點間潛在的相似性越大.然而，真實網絡中存在許多樣本點沒有共同的鄰居，但是在屬性信息方面有極高的相似性，從而導致從共享鄰居角度度量樣本點相似性存在一定的局限.除了這些研究，文獻[24-28]中還提出了許多其它的度量方法.

對于圖數據中樣本點的相似性度量問題，無向無權的圖數據已有了較多的研究.但隨著研究的不斷深入，無向無權圖數據已經不能涵蓋大部分的網絡特性.大部分真實圖數據的鏈接是帶有權重的，比如共同作者網絡、航空網絡等.因此，帶權圖數據中樣本點的相似性度量逐漸受到重視.針對這類問題的研究，本文從屬性信息和拓撲信息2個角度出發，按以下2個步驟來展開工作：①提出基于改進的度中心性指導的隨機游走的方法，度量樣本點基于拓撲信息的相似性；②針對歐式距離在度量相似性方面的不足，通過融合歐式距離和余弦距離來度量樣本點基于屬性信息的相似性，進而得到樣本點間的綜合相似性.

1 預備知識

為了行文簡潔及后文敘述的需要，這里給出文中需要用到的一些基本知識以及相關數學表示.

1.1 帶權圖數據

通常情況下，帶權圖數據可表示為G=(X,R,W)，其中X={x1,x2,…,xn}是一個非空有限集，表示帶權圖數據中樣本點的集合，xi=(xi1,xi2,…,xim)表示有m個屬性的樣本點，即|X|=n,X的矩陣形式表示為

R={rij|i,j=1,2,...,n}表示圖數據中樣本點之間關聯信息的集合，rij表示樣本點xi與xj間的拓撲信息(本文使用樣本點xi與xj基于共享鄰居與非共享鄰居的相異性來刻畫rij)，R也可使用矩陣的形式表示

其中，不妨假設，若rij≠0，則表示樣本點xi與xj有邊相連,反之，rij=0.

帶權圖數據G中樣本點的可達性可作如下定義：若樣本點xi與xj是零步可達，即xi與xj是相同樣本點；若樣本點xi與xj間接連接，即rij=0，但rik0≠0,rk0k1≠0,…,rkl-1j≠0，則稱樣本點xi與xj是l步可達的；若樣本點xi與xj是l步不可達的，則稱為它們恒不可達或者絕對不可達.

1.2 度中心性

在帶權圖數據中，度中心性是衡量一個樣本點與所有其它樣本點相關聯的程度.對于一個樣本點規模為n的帶權圖數據，樣本點xi的度中心性定義為其直接相連鄰居n(xi)所對應的權重之和，可用CD(xi)表示，具體計算方法如下:

其中，T(x)={y|rxy≠0}.

1.3 幾類相似性度量方法

Jaccard相似度是一種從拓撲信息出發，考慮從共享鄰居的數量的角度，度量兩樣本點之間相似性的方法，其具體定義如下

(2)

該指標在縮短計算時間以及尋找最相似樣本點有很好的效果.遺憾的是，該指標著重從最近鄰居考慮樣本點基于拓撲信息的相似性，使得在度量過程中丟失非最近鄰居樣本點的信息.

歐式距離如公式(3)所示，被廣泛應用于的各種相似性度量研究.其優點在于可以克服變量之間的相關性干擾，并且消除各變量量綱的影響.但是該方法易受指標不同單位刻度影響，難以刻畫具有相同歐式距離的屬性信息之間的散度.

(3)

余弦距離如公式(4)所示，是通過計算2個樣本點基于屬性信息的夾角余弦值來評估相似程度.有別于歐氏距離，該方法更加注重度量樣本點基于屬性信息在方向上的差異，但對具體數值的絕對值大小不敏感，使得相似性得分不具有區分性.

(4)

LLRWSMM-PCO方法是一種從屬性信息和拓撲信息2個角度出發，結合隨機游走，進而度量圖數據中兩樣本點相似性的方法.在拓撲信息的相似性度量方面，該方法充分研究了樣本點基于拓撲信息的可達性，并在可達的基礎上，利用隨機游走計算樣本點基于拓撲信息的相似性.在利用余弦相似度計算到屬性信息相似性后，該方法將屬性信息和拓撲信息進行加權，得到最終的相似性，其主要計算公式如下.

(5)

(6)

-SX(xi,xj)表示樣本點xi與xj關于屬性信息的相似性.

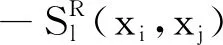
-sij(xi,xj)表示樣本點xi與xj的綜合相似性.

-τ:xi→xko→…→xkl-1→xj表示樣本點xi與xj間的一條隨機游走路徑.

2 基于拓撲信息的相似性度量

針對帶權圖數據中樣本點基于拓撲信息的相似性度量問題，文中從共享鄰居與改進度中心性的角度出發，利用隨機游走的方法，構建了ICSMMP算法.該算法從以下2個方面對拓撲信息進行相似性度量.首先改進了共享鄰居的定義，利用共享鄰居與非共享鄰居的比值構造相鄰樣本點關于拓撲信息的相異性.在此基礎之上，利用改進度中心性指導隨機游走的方法，選擇最優路徑，進而度量帶權圖數據中任意樣本點基于拓撲信息的相似性.

2.1 基于共享鄰居的相似性度量方法

在討論樣本點相似性的算法中，計算樣本點間的連邊概率通常是基于它們的共同鄰居樣本點的信息.從樣本點的共享鄰居的角度出發，2樣本點的共享鄰居越多，共享鄰居對樣本點相似性所做出的貢獻就越大.相反，若2樣本點的共享鄰居越少，則2樣本點潛在的相似性越小.對任意樣本點xi與xj，現有的共享鄰居T(xi,xj)定義為

T(xi,xj)=T(xi)∩T(xj).

(8)

在解決實際問題中，如圖1所示，(a)、(b)中T(x1,x2)={x3}，但 (b)中x1與x3之間的關聯信息比(a)多，所以其在拓撲信息方面潛在的相似性更大.為此，文中在公式(8)的基礎上改進共享鄰居的計算方法，具體公式如下:

T(xi,xj)*=T(xi)+T(xj)-(O(xi)+O(xj))+T(xi,xj),

(9)

其中，O(xi)表示與xi連接的鄰居中與xj不連接的鄰居.

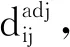
(10)

其中，|T(xi,xj)*|表示共享鄰居的數目.公式(10)表明，樣本點的非共享鄰居越多，其共享鄰居所占的比例越小，樣本點間潛在的關系越少，進而拓撲信息相似性就越低.

2.2 改進度中心性

在帶權圖數據中，樣本點的度中心性是衡量樣本點重要性的重要指標.現有計算帶權圖數據中樣本點度中心性的方法單方面考慮了其鄰居權重，沒有考慮樣本點鄰居個數對度中心性的影響.由公式(1)計算不難發現，圖2中x2與x3的度中心性的值都為1.8，但x2擁有更多的鄰居，在游走的過程中，x2作為游走過程的中間樣本點的可能性更大.為此，在公式(1)的基礎上，本文提出了一種改進的度中心性的計算方法如下

(11)

改進后的度中心性綜合考慮樣本點的鄰居個數、連邊的權重，能夠更加全面的反映這2個因素對樣本點重要性的影響.

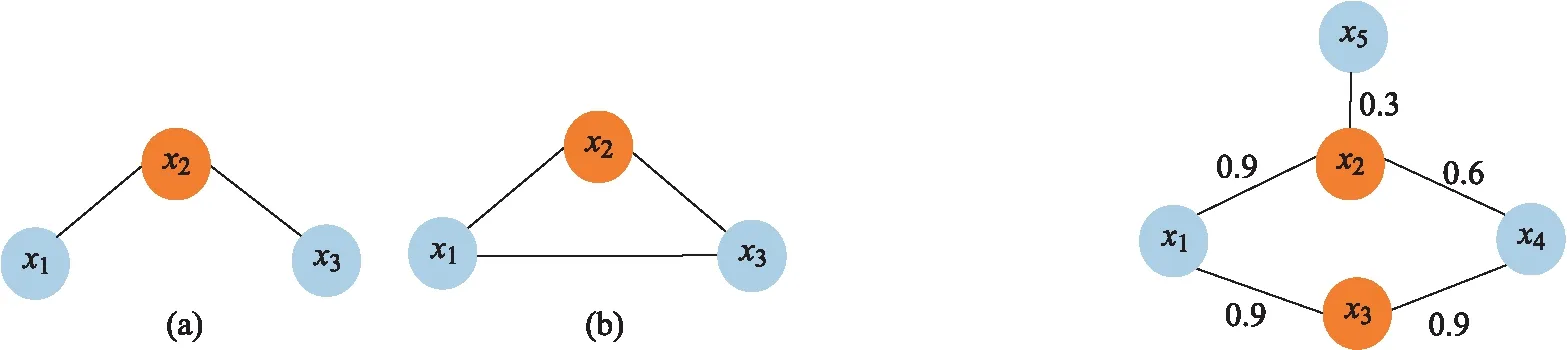
圖1 樣本點x2的共享鄰居 圖2 鄰居個數不同但權重之和相同的樣本點

2.3 基于改進度中心性指導的隨機游走方法

在充分研究了樣本點的度中心性后，本文以改進度中心性指導樣本點的隨機游走，度量帶權圖數據G中任意樣本點基于拓撲信息的相似性.一般的，在G中拓撲結構是連通的時候，從樣本點xi出發，經過有限次的游走可達樣本點xj，兩樣本點通過有限中間樣本點連接，在拓撲信息方面具有潛在的相似性.而在游走的過程中，會產生多條隨機游走路徑，且基于不同路徑計算相似性的結果不同.為此，我們提出了公式(12)來選擇最優路徑進行相似性度量

(12)

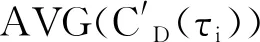
(13)

其矩陣項表示圖數據中樣本點的相異性，具體計算方式如下

(14)

不難發現，基于改進度中心性指導隨機游走的方法不僅考慮樣本點自身的信息，而且將樣本點鄰居蘊含的潛在信息和一定范圍內共享鄰居與非共享鄰居的信息作為因素考慮在相似性的度量過程中，避免度量過程僅僅考慮最近鄰相似性，使得相似性難以區分.在解決實際問題中，利用隨機游走度量方法最關注的游走路徑長度是3步，通過3步游走可達的2個樣本點具有很高的相似性.相反，游走路徑超過3步的樣本點，其潛在的拓撲相似性減少.為此，文中定義若游走路徑長度超過3步，則2樣本點不可達.

3 樣本點的綜合相似性度量

針對歐式距離和余弦距離這2種度量方法在單一使用中的不足，構建了一種融合方法來計算樣本點屬性信息的相似性.具體如公式(15)所示，

(15)

分別對樣本點的屬性信息和樣本點間的拓撲信息的相異性進行全面的討論后，文中綜合樣本點基于屬性信息和樣本點間拓撲信息的相異性，給出公式(16)來定義帶權圖數據G中樣本點的綜合相異性矩陣D=(dij)n×n，其中

(16)

最后，將相異性矩陣轉化為相似性矩陣S=(Simij)n×n，進而得出綜合性的樣本點相似性度量方法，相似性矩陣S的矩陣項的計算方式如下：

(17)

由可達的相關知識不難發現，本文研究相似性度量問題可分為3類進行研究：0步可達，l 步可達和不可達，處于不同類別的樣本點的相似性計算方式不同.針對本文的研究目的，“基于改進度中心性的樣本點相似性度量方法”可以總結為ICSMMP算法.

4 ICSMMP算法

輸入 無向帶權圖數據G=(X,R,W).

輸出 帶權圖數據G的相似性矩陣S=(Simij)n×n.

步驟1 由公式(10)計算相鄰樣本點基于共享鄰居的相異性.

步驟2 由公式(11)計算帶權圖數據G中各樣本點的改進度中心性.

步驟3 調用隨機游走算法，基于公式(12)，選擇最優路徑.

步驟4 基于最優路徑，使用公式(14)計算樣本點基于拓撲信息的相異性.

步驟5 由公式(15)計算樣本點屬性信息的距離.

步驟6 由公式(16)、(17)計算G中各樣本點的綜合相似度.

5 算例分析

本文使用了隨機生成的帶權圖數據G，該圖數據有10個樣本點，12條邊，為了更好的說明本文所提出的ICSMMP算法，本文將G進行可視化，其結果如圖3所示，并在改進度中心性指導的隨機游走方法下度量樣本點相似性.圖4中樣本點大小表示該樣本點的改進度中心性大小，樣本點越大表示改進度中心性越大(藍色樣本點代表當前樣本點，黃色、灰色、綠色、橙色分別代表從當前樣本點出發游走1步、2步、3步和4步到達的樣本點).表1為G中10個樣本點的屬性信息.

圖3 帶權圖數據G的拓撲結構

圖5與圖6展示了在帶權圖數據G中的樣本點基于ICSMMP方法與LLRWSMM-PCO方法下的相似性矩陣的熱圖.鑒于樣本點間的相似性存在對稱性，所得到的相似性為關于對角線對稱的矩陣.從圖5、6易知，ICSMMP方法與LLRWSMM-PCO方法在區分樣本點間拓撲信息的相似性，捕獲樣本點間的鄰居相似性方面有不錯的效果，且2種方法也能夠從數值上明顯的區分樣本點間拓撲信息的相似性.但從表2分析，不難發現，在識別最相似樣本點方面，基于ICSMMP方法，x2最相似的樣本點為x1，而在LLRWSMM-PCO方法下，x2最相似的樣本點為x4.很明顯x2與x1不僅在屬性信息方面有更高的相似性，在拓撲信息方面，x2與x1有更多的共享鄰居和更相似的拓撲結構，所以它們具有更多潛在的相似性.

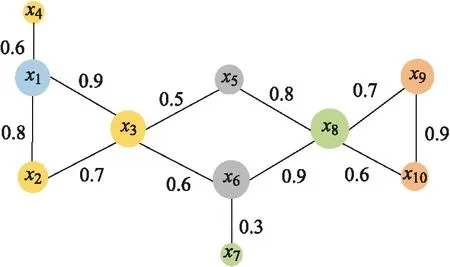
圖4 x1與其它樣本點的游走路徑長度

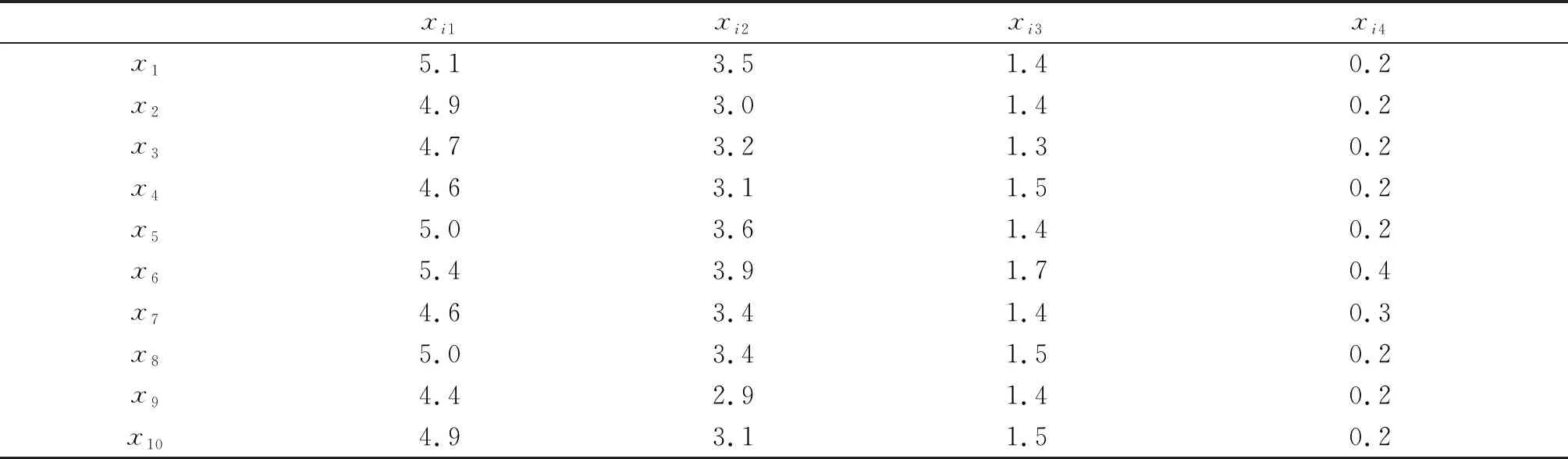
表1 樣本點的屬性信息

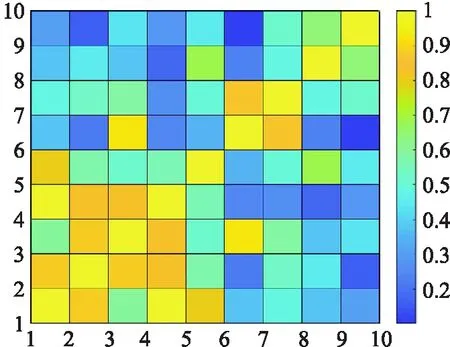
圖5 基于ICSMMP的相似性度量方法

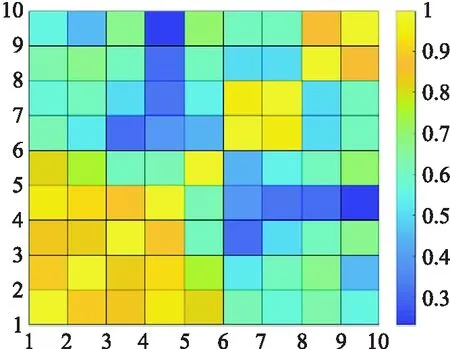
圖6 基于LLRWSMM-PCO的相似性度量方法

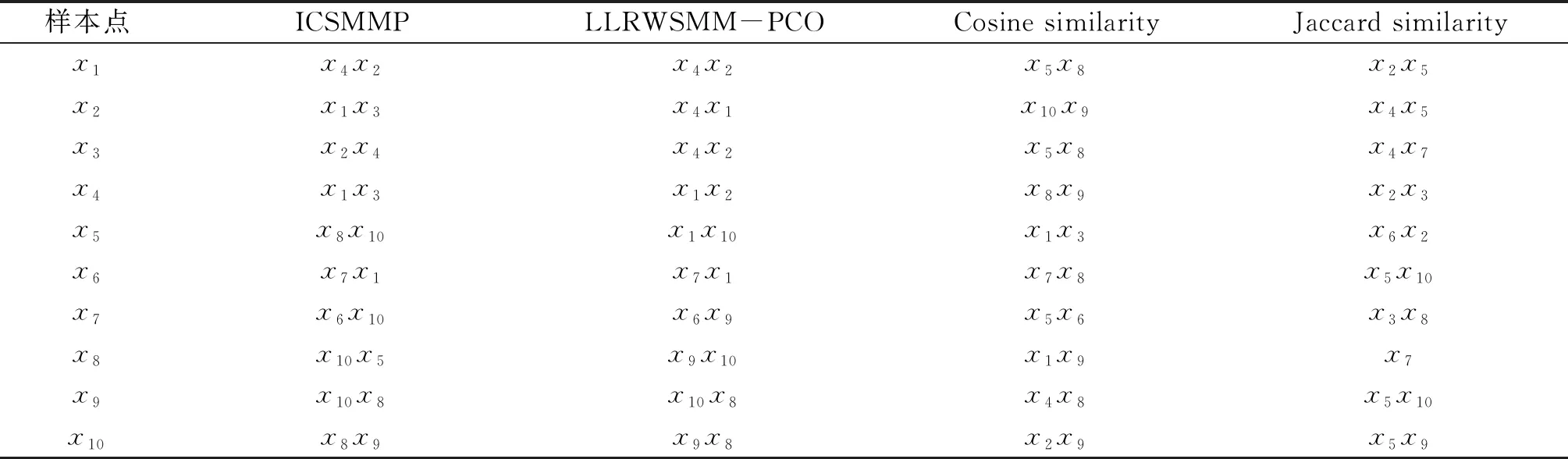
表2 G中樣本點最相似的2個樣本點

圖7與圖8分別是基于余弦距離方法與Jaccard相似性方法下的相似性矩陣的熱圖.從圖中分析，余弦距離方法從單一屬性信息的角度出發，未考慮拓撲信息的相似性，使距離較遠，拓撲信息相似度較小的樣本點可能被識別為高相似樣本點.如表2的數據可知，在余弦距離方法下，樣本點x1與x8，x2與x10，2組樣本點對利用余弦距離方法計算得出的相似度很高，但是兩樣本點沒有共同鄰居，且拓撲結構的相似性也很低.Jaccard相似性方法是從拓撲信息角度出發，計算樣本點的相似性.該方法能夠很好的捕獲鄰居樣本點的相似性，不足的是，該方法從鄰居樣本點的單一角度出發，損失了很多非鄰居樣本點的信息，即沒有共同鄰居的樣本點對相似度為0，并且沒有考慮屬性信息，使得大部分樣本點成為一般樣本點.

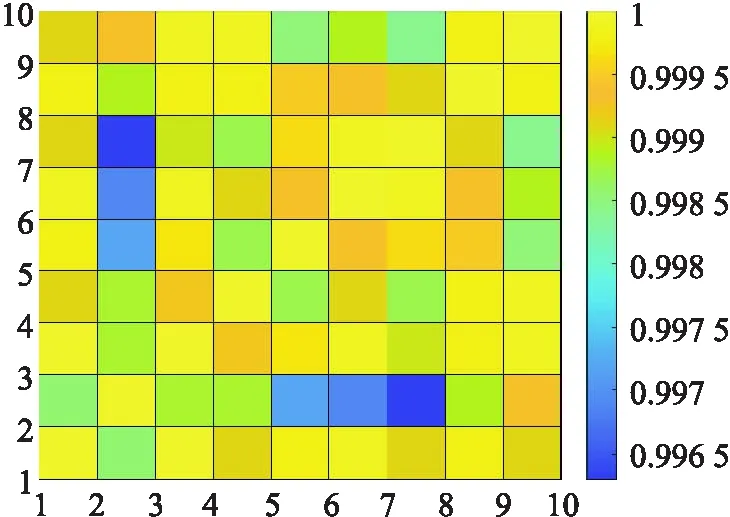
圖7 基于余弦距離的相似性度量方法

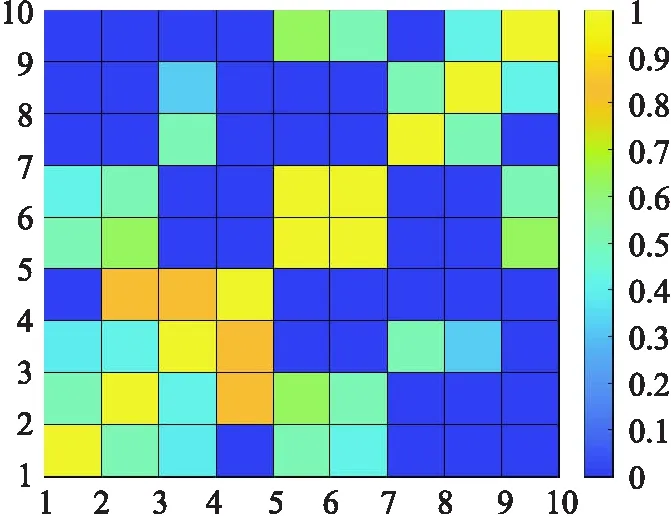
圖8 基于Jaccard相似度的相似性度量方法

圖9是分別通過4種相似性度量方法計算所得的擁有相同相似度值的樣本點對所占比值.不難看出，通過ICSMMP的相似性度量方法計算得出的100組相似值中，相似度值相同樣本點對所占比值最低，說明該方法得出的相似度值中，不存在多對樣本點擁有相同的相似性得分，從而能很好的識別最相似樣本點.但是在LLRWSMM-PCO方法、余弦距離方法和Jaccard相似性方法下，存在多對樣本點擁有相同的相似性得分，這樣可能使得處于同一階段相似性的樣本點不易區分，不利于后續圖數據聚類或識別圖數據中重要樣本點的工作的進行.

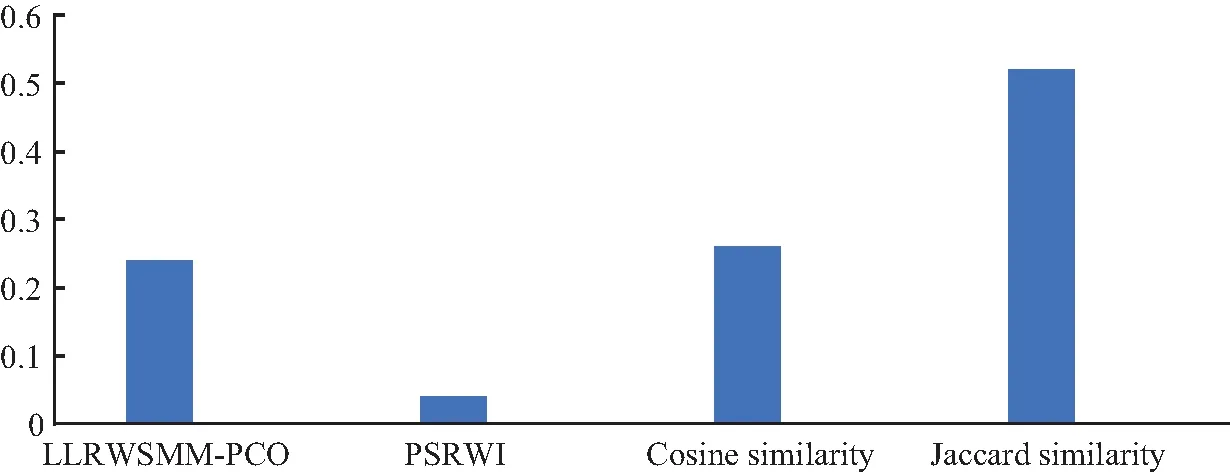
圖9 同一階段相似度占總相似度比值示意圖

6 結語

針對帶權圖數據中樣本點的相似性度量問題，從樣本點的屬性信息和拓撲信息角度出發，構建了一種基于改進度中心性的樣本點相似性度量方法.實驗結果表明，該方法不僅能很好的區分樣本點間關于拓撲信息的相似性，捕獲樣本點間鄰居的拓撲相似性，而且在數值上能夠明顯的區分各個樣本點間的相似性得分.