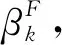一類改進的譜共軛梯度法

陳秀芳，李 鋒

(1.滇西科技師范學院 數理學院 ，云南 臨滄 67700;2.云南師范大學 數學學院 ，云南 昆明 650500)

考慮如下無約束優化問題

(1)

其中：函數f:Rn→R上是連續可微函數.共軛梯度法(CG法)是Stiefel與Hestenes于1952年提出了一種求解線性方程組的算法,隨后，Reeves與Fletcher在1964年將該方法推廣到求解非線性優化問題，提出了如下非線性共軛梯度法[1]：

xk+1=xk+αkdk,k=0,1,2，

(2)

其中xk為當前迭代點，搜索步長αk由合適的線搜索(精確和非精確)確定，搜索方向dk由以下公式給出：

(3)

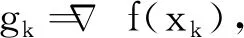
共軛梯度法具有占用存儲空間小、收斂速度快的特點，廣泛應用于控制科學、工程管理和流程研究等領域，在近年來興起的大數據科學顯示出特別的吸引力，因而一直受到學者們的廣泛關注，相關研究持續不斷.

共軛梯度法的改進線索大致分為2條，一條是修改共軛系數βk(稱這類算法為經典CG算法)，另一條是融合譜最速下降法的思想，引入譜系數(稱這類算法為譜共軛梯度法).

經典CG算法分為2類：第1類包括Fletcher-Reeves(βkFR)[2]、Dai Yuan(βkDY)[3]公式如下：

(4)

其中‖·‖為Euclidean范數，yk=gk+1-gk，這些方法有很好的收斂性，然而數值性能卻不是很好.另一類包括Polak-Ribiére-Polyak(βkPRP)[4]、Hestenses-Stiefel(βkHS)[5]、Liu Storrey(βkLS)[6]，它們的βk公式分別如下:

(5)

這類方法收斂性分析不是很理想，然而數值實驗結果較為良好，且PRP方法和HS方法被公認為最有效的CG法.鑒于上述2類方法優缺點互補的特點，學者們提出了把2種系數組合起來的混合共軛梯度法.2006年Wei等[7]提出一個新的共軛參數βk，βk與經典的PRP公式有類似的形式，并且首次將線性組合的思想引入經典共軛梯度法中，公式如下：

(6)

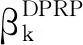
(7)

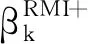
(8)

韋等在復雜線搜索下建立了新的PRP型共軛梯度法，并討論相關的問題.

鑒于經典CG算法是基于最速下降的改進算法，2001年Birgin和Martinez[12]基于譜梯度法提出了譜共軛梯度法(SCG法)，即在經典共軛梯度法的搜索方向dk的迭代格式(3)中引入譜系數δk：

(9)

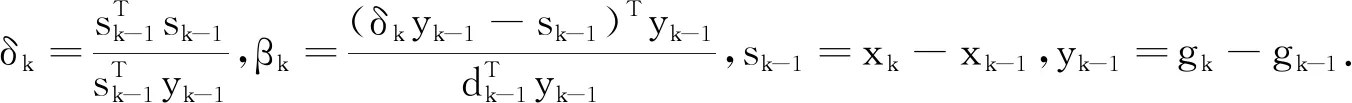
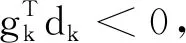
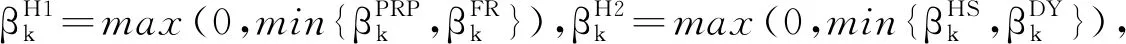
對應的參數分別為：

(10)

景書杰等在Armijo線搜索下證明算法全局收斂，綜合前面2條線索，得到一個好的結果.沿著這個線索，大有工作可做.有關譜共軛梯度法的其他變種還很多，可以參看文獻[17-21].

文中深受上述討論的啟發，尤其是文獻[11]和[16]中2個參數的構造.從這些算法的發展可以發現，確定不同的系數，算法的表現不一樣.文中嘗試用前面的思路確定2個系數的新公式，并討論他們的收斂性及相關問題，其它工作安排如下：第1節算法及其下降性，第2節算法的全局收斂性，第3節數值實驗，第4節全文總結.

1 算法及其下降性

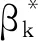
(11)

其中，

(12)

該算法采用修正的強Wolfe線搜索求步長

其中,0<ρ<σ<1.

算法1：

譜共軛梯度法算法流程如下：

Step 0 初始值x0∈Rn,ε>0,令μ>0,λ>0,0<ρ<σ<1,k:=1,d1=-g1,Step 1 計算gk,若‖gk‖≤ε,則停止,否則轉Step 2,Step 2 用強Wolfe線搜索公式計算αk,Step 3 用式(11),(12)分別計算dk,βFk,δk,Step 4 令xk+1=xk+αkdk求gk+1,并用式(11)求βFk+1,使得dk+1=-δk+1gk+1+βFk+1dk,使得k:=k+1,轉Step1.

算法的收斂性證明需要以下假設條件成立

假設A[21]：

(i)定義目標函數f(x)在水平集L0={x∈Rn|f(x)≤f(x0)}上有下界，x0是初始點.

(ii)目標函數f(x)二次連續可微，它的梯度函數g(x)是Lipschitz連續，則存在常數L>0,使得：‖g(x)-g(y)‖≤L‖x-y‖,?x,y∈N.

(iii)目標函數f(x)在Rn中是二階連續可微的一致凸函數.

以下給出算法A的充分下降條件.在共軛梯度法的收斂性分析中，通常都有以下幾個經典的引理，文中證明了相應的結果.

引理1.1假設{gk}和{dk}是由算法1產生的序列，則滿足充分下降條件

1) 對?k≥1，如果‖dk‖≠0,‖gk‖≠0，則有

(13)

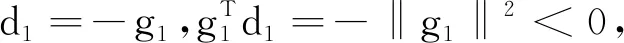
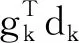
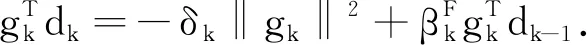
由(13)式得

于是有

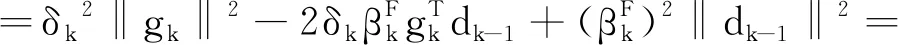
綜上，引理1.1得證.

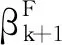
(14)

證明：由式(12)和假設A得

(15)

將‖gk+1‖>3Lαk‖dk‖代入(15)式即得所要結論.

引理1.3若假設A成立，?k>0,gk,dk≠0，則由算法1生成的序列{gk}和{dk}滿足Zoutendjik條件

(16)

此外，由Lipschitz條件有 (gk+1-gk)Tdk≤αkL‖dk‖2.

以上2式結合得

(17)

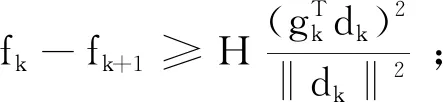
(18)

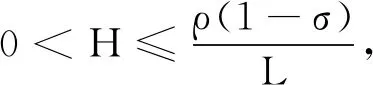
即引理1.3成立

2 算法的全局收斂性

根據前面的引理部分，也能得到如下的收斂性證明.

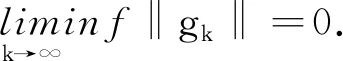
證明：反證法，若結論不成立，就一定有常數ζ>0，滿足任給k≥0,

‖gk‖≥ζ.

(19)

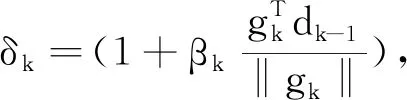
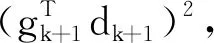
顯然與引理1.3相矛盾，故定理2.1成立.

3 數值實驗

本節中，為測試新方法的數值計算效果而建立數值實驗，在強Wolfe線搜索下，文中的譜共軛梯度為記為PCSWP；在一般Wolfe線搜索下，建立共軛梯度法的數值實驗，記為CWWP,分別與文獻[16]的方法作對比，記為JPSWP法，測試問題選自文獻[7]中的部分函數，算法的終止條件為‖gk‖≤10-6，或算法迭代次數超過 10 000，所有代碼均在Matlab2016a中進行，數值結果以NI,NF,NG的形式給出，NI是算法迭代次數，NF是目標函數計算次數，NG是梯度函數計算次數，“*”指算法運行失效，經過各種嘗試和嚴格的對比后，各參數的取值如下：PCSWP法中的參數μ=0.01,λ=0，CWWP法中參數μ=0.01,λ=0，而文獻[16]中作者只是在Armijo線搜索下分析算法的全局收斂性，并未進行數值實驗，故本文在強Wolfe線搜索下建立，且μ=1.1

各測試結果如表1：

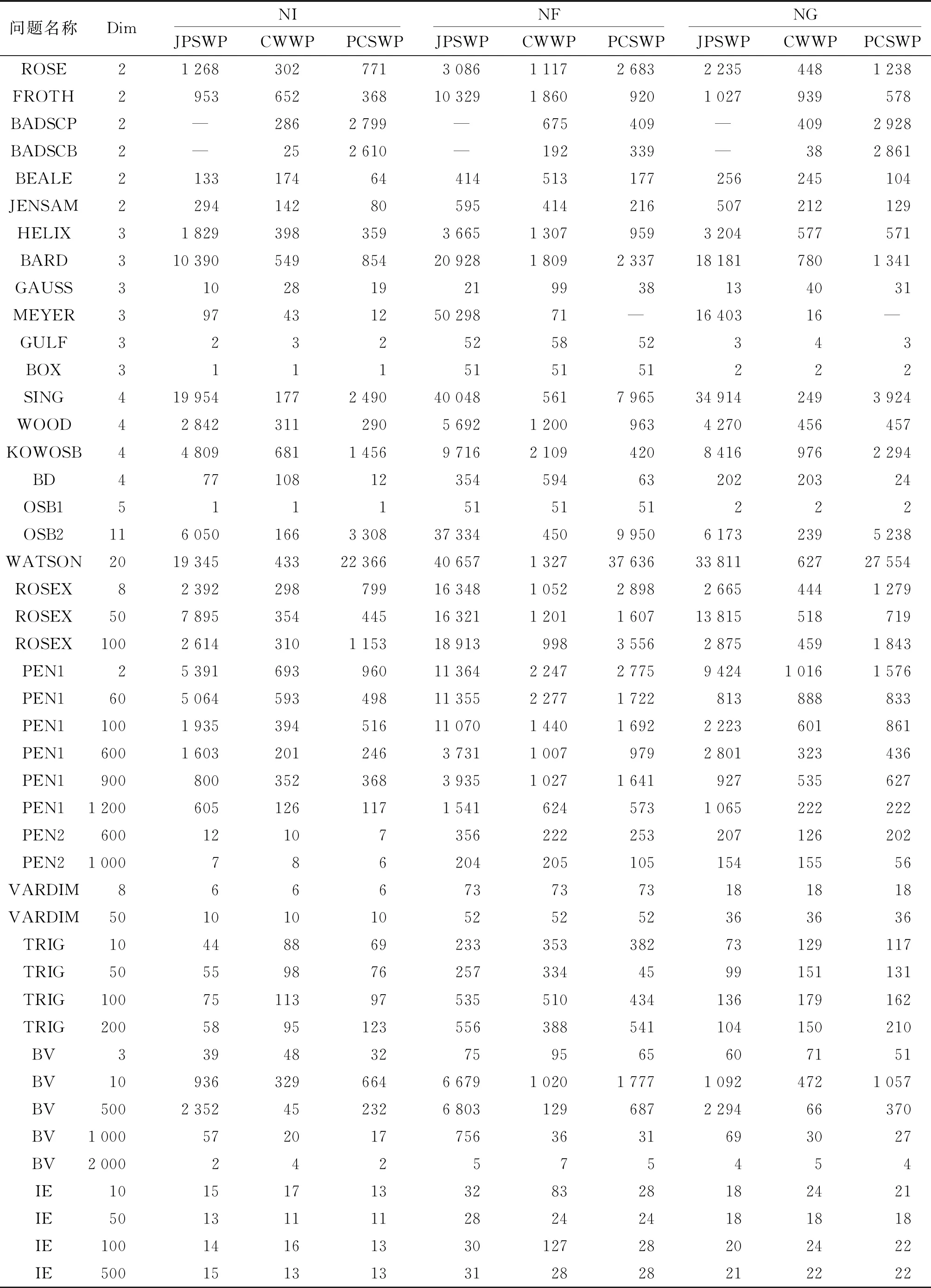
表1 不同問題各算法測試結果表

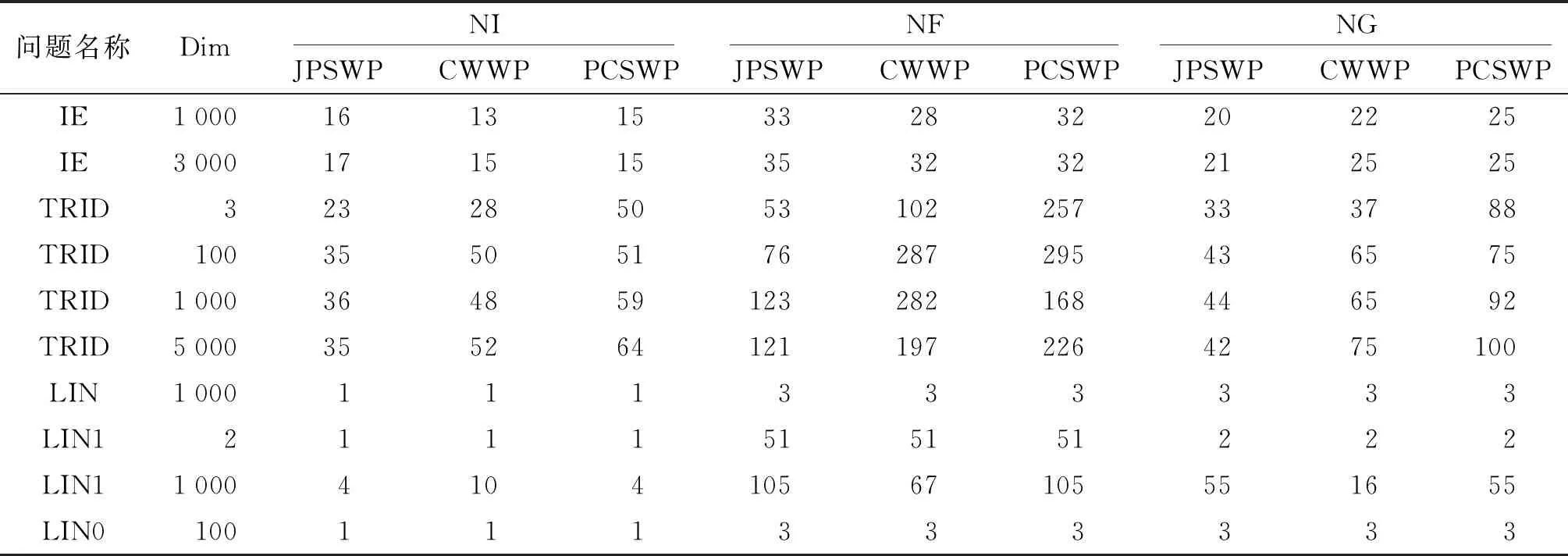
續表1

從表格中可以看出，對于絕大部分測試問題，在強Wolfe線搜索下，本文提出的譜共軛梯度法(PCSWP)比文獻[16]中的譜共軛梯度法(JPSWP)更有效，算法更具有競爭力，算法的迭代次數、目標函數的計算次數和梯度函數計算次數等方面均能達到最小.極少數測試問題上，求解GAUSS函數和WATSON函數時，JSWP法更有效；另外，本文在進行數值實驗時，放寬線搜索條件，在一般Wolfe線搜索下，CWWP法比JSWP法和PCSWP法更有效；還有極少數問題，是無論選什么方法，測試結果都一樣.綜上，本文提出的譜共軛梯度法更有效，具有更好的數值性能.

4 結語