基于有效精度的Logistic混沌方程計算軌道偏離研究

王佳音，宋大全，侯夢瑜，朱巍偉，劉嘉輝*

(1.哈爾濱理工大學 計算機科學與技術學院，黑龍江 哈爾濱 150080；2.牡丹江師范學院 學術理論研究中心，黑龍江 牡丹江 157011)

混沌方程研究中存在的一個關鍵問題是真實軌道難以在計算機中實現.混沌方程的計算需要精度不斷擴展，隨著迭代次數的增加，計算機系統中的浮點運算已經難以滿足精度擴展的要求.計算機系統中的實數表示范圍雖然很大，但其有效的精度卻受到一定的限制，這種限制對于混沌方程的計算非常不利.Logistic混沌方程是典型的研究混沌的模型，被廣泛用于隨機數發生器、密碼算法、人口分布研究和物理數學方程等領域中.在計算機系統中研究Logistic混沌方程需要進行離散化軌道處理，即不能使用連續的實數區間表示其軌道的數值，因此，離散的計算軌道與最初的原始軌道的規律變化成為關注的重點.Logistic混沌方程在計算機系統中的計算軌道是由計算機系統中浮點運算實現的.本文介紹計算機系統中數值表示的基本形式和浮點數的標準，給出Logistic混沌方程真實軌道的基本定義以及軌道點的精度變化規律，對Logistic混沌方程的計算軌道進行詳細分析，給出對比實驗和一些推論.

1 計算機中數值的標準化形式

數值可以采用科學記數法來進行標準化：

±(d0.d1 d2 d3)…×Be.

(1)

其中，“±”代表該數值的符號，即正數或者負數；“d0”代表該數值的小數點前整數部分的第一位數字位；“.d1 d2 d3”代表該數值的小數點后的第一位、第二位、第三位數字位等；“e”代表該數值的指數；“B”代表基數，即十進制數值、八進制數值、二進制數值等.

在程序設計語言中，可以用整數和實數等表示計算數值.實數是最常用的一種數值表示方法，可以分為單精度和雙精度兩種.很多計算機系統中采用浮點數表示法表示數值.IEEE 754浮點數標準一般用{S,E,M}表示一個浮點數.

在IEEE 754浮點數標準的單精度浮點數結構中(圖1),S(Sign)占1 Bit，代表該數值的符號位，即“±”正數或者負數,E(Exponent)占8 Bit，代表該數值的公式(1)科學記數法的指數部分,M(Mantissa)占23 Bit，代表該數值的有效數字部分，有效數字部分也被稱為尾數位.一個二進制的浮點數F可以表示為：

F =(-1)S×M×2E.

(2)

其中，S符號位可以決定該數值是正數還是負數.

IEEE 754浮點數標準的64位雙精度浮點數結構如圖2所示.符號位S占1 Bit，指數部分E占11 Bit,尾數部分占52 Bit.

從圖1和圖2中可以看出，計算機能夠表示的數值非常大.在32位單精度浮點數中，可以表示的最大正實數約為3.402 823×1038，最小的正實數約為1.175 494×10-38，所表示數值的有效數字位由M(Mantissa)尾數位控制.

圖1 32位單精度浮點數結構圖 圖2 64位雙精度浮點數結構圖

定義1計算機系統中實數的有效精度是計算機中所表示的實數能夠標準化表示為公式(1)的形式，十進制標準的該數值小數點后有效數字位的個數定義為該數值的有效精度.

由IEEE 754的32位單精度浮點數的結構可以看出，該數值的有效精度是由Mantissa決定的.在微軟的操作系統Windows中的float.h文件中，一般性地描述了ANSI浮點運算,“This file contains defines for a number of implementation dependent values which are commonly used by sophisticated numerical(floating point)programs.[ANSI]”.在該文件中，單精度浮點數的有效精度定義為：#define FLT_DIG 6/* # of decimal digits of precision */.float類型的單精度浮點數能保證的十進制有效精度是6位.單精度對于普通的計算能夠滿足基本的要求，而對于科學計算可以使用雙精度double類型，在float.h文件中，其定義為：#define DBL_DIG 15/* # of decimal digits of precision */.double類型的雙精度浮點數能保證的十進制有效位數是15位.

2 Logistic混沌方程的真實軌道

Logistic混沌方程定義為：

x[n+1]=a×x[n]×(1-x[n]).

(3)

其中，x[n]是Logistic混沌方程隨著時間變化的序列，x[n]的值在0和1之間.x[0]是Logistic混沌方程的初始值，a是Logistic混沌方程的控制參數，a的值在3.6和4之間是混沌區域.

定義2Logistic混沌方程的真實軌道是由Logistic混沌方程公式(3)中的x[n]的真實值組成的點軌跡.

Logistic混沌方程的真實軌道在目前的計算機中是很難實現的.

假設Logistic混沌方程的初始值x[0]=0.77，給定控制參數a=3.99.計算過程為：

x[1]=a×x[0]×(1-x[0])

=3.99×0.77×(1-0.77)

=0.706 629.

因此，x[1]=0.706 629.將x[1]帶入下一次迭代運算.計算過程為：

x[2]=a×x[1]×(1-x[1])

=3.99×0.706 629×(1-0.706 629)

=0.827 144 780 872 41.

因此，x[2]=0.827 144 780 872 41.繼續進行下一次迭代計算.計算過程為：

x[3]=a×x[2]×(1-x[2])

=3.99×0.827 144 780 872 41×

(1-0.827 144 780 872 41)

=0.570 475 406 468 291 948 355 210

159 681.

因此，x[3]=0.570 475 406 468 291 948 355 210

159 681.

繼續迭代的計算過程為：

x[4]=a×x[3]×(1-x[3])

=3.99×0.570 475 406 468 291 948 355

210 159 681×(1-0.570 475 406 468 291

948 355 210 159 681)

=0.977 682 536 161 684 843 293 825 121

525 298 332 899 560 454 680 759 943 093

173 61.

因此，x[4]=0.977 682 536 161 684 843 293 825 121 525 298 332 899 560 454 680 759 943 093 173 61.

當Logistic混沌方程迭代一次時，x[1]的有效精度是6.

當Logistic混沌方程迭代第二次時，x[2]的有效精度是14.

x[2]的有效精度是控制參數a(3.99)的小數部分,有效精度是2，與實數x[1](0.706 629)的有效精度是6，以及實數(1-x[1])的有效精度是6.計算它們的和，2+6+6=14.由此可見，x[3]的有效精度是：2+14+14=30.x[4]的有效精度為：2+30+30=62.x[5]的有效精度為：2+62+62=126.表1給出了Logistic混沌方程迭代的有效精度值.

表1 Logistic混沌方程迭代的有效精度

由于篇幅有限，以下是省略了x[n]的中間有效數字位的真實值，其組成是小數點后10位有效數字位和自末位起的最后10有效數字位.其中，

x[5]=0.087 059 384 6…141 427 592 1.

x[6]=0.317 125 392 2…256 110 184 1.

x[7]=0.864 061 942 5…053 787 688 1.

x[8]=0.468 661 018 8…339 902 376 1.

x[9]=0.993 581 294 3…080 853 672 1.

x[10]=0.025 446 248 4…703 269 544 1.

顯然，以目前的計算機系統中的浮點運算法則難以實現混沌真實軌道的計算.從表1可以看出，Logistic混沌方程在迭代到第11次時，有效精度已經達到1萬位以上，第12次已經超過3萬位的有效精度.在目前的計算機系統中，在如此巨大有效精度下觀察混沌軌道是很難實現的.

3 Logistic混沌方程的計算軌道

定義3Logistic混沌方程的計算軌道是由x[n]在計算機系統的單精度、雙精度或者其他浮點運算形式下獲得的x[n]的值組成的點軌跡.

分別對Logistic混沌方程進行有效精度為1至6的單精度計算.在計算軌道的數值處理中，當計算的數值超過給定的有效精度時，采用截尾的處理方式.在IEEE 754標準中，Mantissa位中如果超出了最大的比特數，溢出的位進行截尾處理.因此，在Logistic混沌方程計算的過程中，對于給定的有效精度P，在每次Logistic混沌方程迭代計算軌道的數值x[n]所獲得的是當前有效精度下的截尾的數值.圖3表示的是有效精度小于等于4時計算軌道與真實軌道的對比圖.在圖3中，P代表計算機系統給定的有效精度，即在計算軌道中獲得的實數x[n]數值的小數部分有效數字的個數.“real”代表Logistic混沌方程的真實軌道的x[n]軌道序列值.

圖3 有效精度小于等于4時計算軌道與真實軌道的對比圖

當計算軌道P=1時，獲得的Logistic混沌方程的x[n]小數部分在十進制表示下只能有一位有效數字位.科學記數法表示的形式為：d1×10-1.當計算軌道P=2時，獲得的實數x[n]的小數部分在十進制表示下只能有二位有效數字位.科學記數法表示的形式為：d1.d2×10-1.當計算軌道P=3和4時，表示形式分別為：d1.d2 d3×10-1和d1.d2 d3 d4×10-1.其中，{d1,d2,d3,d4}分別是十進制的數字{0,1,…,9}.

按照表1中Logistic混沌方程真實軌道x[n]的精度，當Logistic混沌方程迭代15次時，其精度已經超過了10萬位.x[15]的精度是131 070位，遠遠超過了大部分計算機硬件和計算軟件所允許的最大精度.因此，本文只統計前15次迭代值，并對Logistic混沌方程的計算軌道和真實軌道進行對比分析.

從圖3可以看出，在P=1,2,3,4時，第一次迭代的值均接近0.7.第二次的迭代值均在0.8附近，而且P=1的計算軌道的x[n]開始偏離真實軌道“real”.當第三次迭代時，P=2的計算軌道開始偏離真實軌道“real”，其情形與第二次迭代時候P=1的計算軌道接近.從第三次迭代可以看出，P=1的計算軌道偏離真實軌道“real”逐漸加大；當迭代到第四次時，P=1的計算軌道已經遠遠的與真實軌道“real”以及其他計算軌道分離.在第五次迭代之后，P=1的計算軌道出現了短周期循環：0.3->0.8->0.6->0.9.在第七次迭代時，P=1，2，3的計算軌道均與真實軌道“real”分離.P=4的計算軌道在第11次迭代時與真實軌道“real”分離.從圖3可以看出，當P=4時，從第11次迭代之后，其與真實軌道“real”的偏離距離逐漸加大.不僅如此，各個計算軌道也逐漸增加了軌道偏離距離.

由以上的分析可以獲得如下的基本推論：

推論1Logistic混沌方程的計算軌道和真實軌道隨著迭代次數的增加，計算軌道逐漸與真實軌道分離.

推論2計算機的有效精度很大程度上影響著Logistic混沌方程的計算軌道與真實軌道的分離速度.

為進一步驗證推論2，對P=5和P=6的計算軌道實現進一步的研究,在分別進行P=5和P=6的計算軌道計算后，該計算軌道的x[n]與真實軌道的序列值進行差值計算，獲得其絕對差值.

圖4表示當有效精度是5和6時計算軌道與真實軌道的差值圖.圖中“1E”代表10的冪，“1E-6”代表10-6，“1E-5”代表10-5，以此類推.

從圖4可以明顯看出，當有效精度是6時，即P=6時，其與真實軌道的差值明顯小于計算軌道P=5.圖4中一個明顯的趨勢是：隨著迭代次數的增加，計算軌道明顯偏離了真實軌道，當P=5的計算軌道在第一次迭代時與真實軌道的誤差接近0.000 01，在第15次迭代時接近0.1，前后相差104倍.

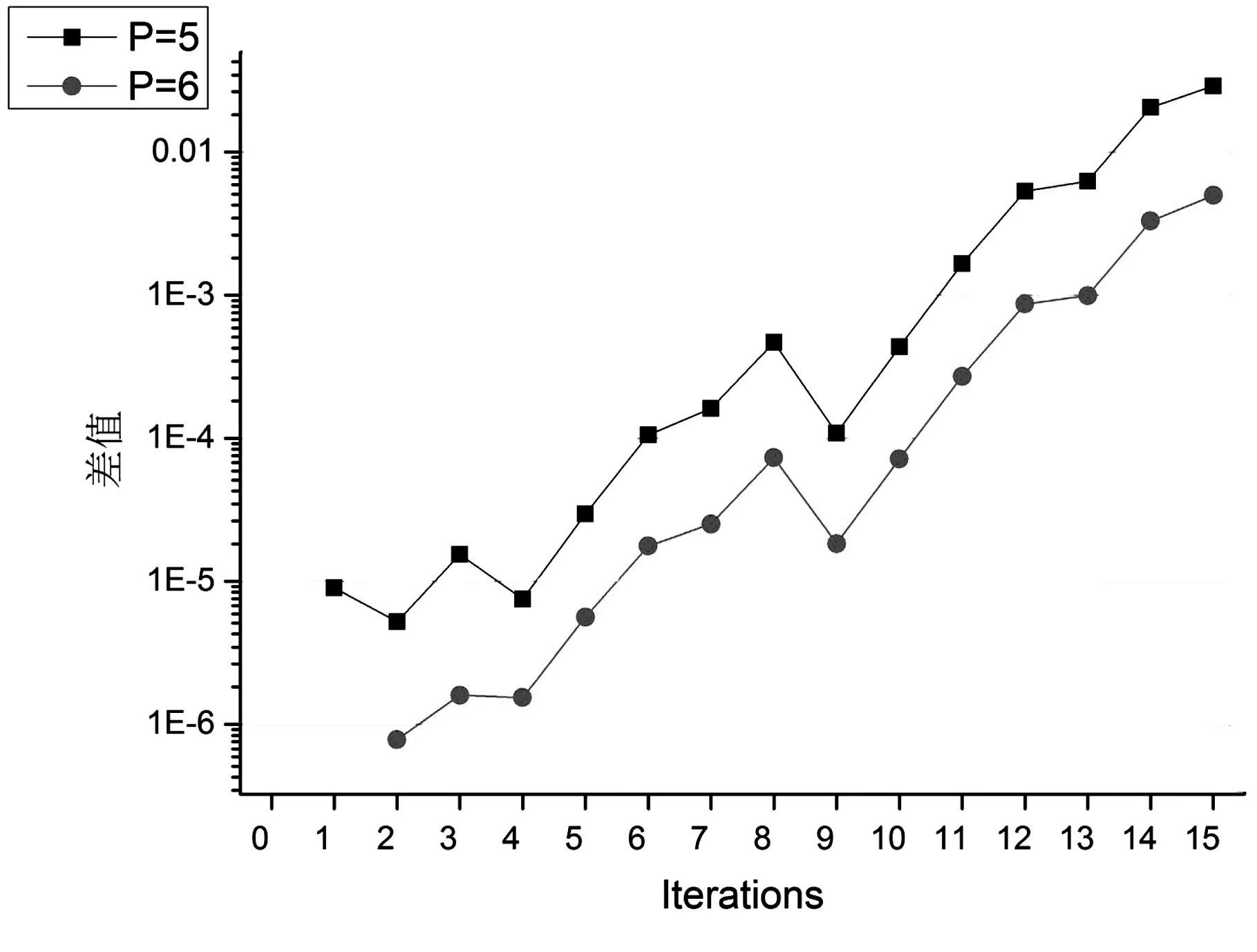
圖4 當有效精度是5和6時計算軌道與真實軌道的差值圖

當計算軌道P=6時，第一次迭代差值等于0是因為在表1中,x[1]的有效精度是6，而計算軌道P=6時,其有效精度也等于6，因此，其差值等于0.但是，隨著迭代次數的增加，計算軌道逐漸偏離了真實軌道.計算軌道P=5偏離真實軌道的速度明顯快于計算軌道P=6.

4 結論

Logistic混沌方程的真實軌道與計算軌道的研究是混沌理論研究中一個重要的分支，通過計算軌道的分析，可以分離出不同計算軌道的基本特征及其變化的基本規律，為混沌的計算軌道的進一步研究提供了一定的基礎，對未來進一步研究混沌計算軌道的規律和特點進行了有益的探索.