解2022年新高考I卷第12題的本手、俗手、妙手*
安愷凱
(江蘇省天一中學 214101)
沈丹丹
(江蘇省無錫市東北塘中學 214101)
“本手、俗手、妙手”是2022年語文新高考I卷的作文題,本意是圍棋的三個術語,本手是指合乎棋理的正規下法;妙手是指出人意料的精妙下法;俗手是指貌似合理,而從全局看通常會受損的下法.筆者不禁想到,在數學解題過程中不也會經常遇到正規解法、精妙解法以及貌似合理卻錯誤的解法嗎?筆者便結合2022年數學新高考I卷第12題來做一篇“數學作文”.
1 問題呈現
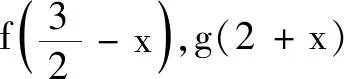
C.f(-1)=f(4) D.g(-1)=g(2)
新高考的實施對函數對稱性的考查不減反增,例如,在2022年全國新高考I卷中,第6題考查了三角函數的對稱性,第10題考查了三次函數的對稱性,而作為多選題壓軸的第12題考查了抽象函數的對稱性.抽象函數由于沒有給出具體的表達式,因此對學生的數學抽象和邏輯推理素養提出了更高的要求,同時結合多選題層次更為豐富、角度更為多元的題型特征,更能考查學生辯證思維和深度思考的能力.
在上面的問題中,選項BCD的突破需要學生掌握好三招“本手”:一為“如何由f(kx+b)的奇偶性求f(x)的對稱性”;二為“如何由f(x)的對稱性求f′(x)的對稱性”;三為“如何由f(x)的兩個對稱性求f(x)的周期性”.筆者將上述三個問題一般化處理后進行探究,生成如下一般性結論.
2 本手
結論1若f(kx+b)(k≠0)為偶函數,則f(x)關于x=b對稱;若f(kx+b)(k≠0)為奇函數,則f(x)關于(b,0)對稱.
證明若f(kx+b)為偶函數,則f(-kx+b)=f(kx+b),故f(x)關于x=b對稱.若f(kx+b)為奇函數,同理可證.
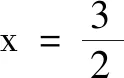
結論2若f(x)關于x=m對稱,則f′(x)關于(m,0)對稱;若f(x)關于(m,0)對稱,則f′(x)關于x=m對稱.
證明若f(x)關于x=m對稱,則f(x+m)=f(m-x),兩邊求導可得f′(x+m)=-f′(m-x),所以f′(x)關于(m,0)對稱.若f(x)關于(m,0)對稱,同理可證.

結論3若f(x)關于x=m和x=n對稱,則T=2|m-n|為f(x)的一個正周期;若f(x)關于(m,0)和(n,0)對稱,則T=2|m-n|為f(x)的一個正周期;若f(x)關于x=m和(n,0)對稱,則T=4|m-n|為f(x)的一個正周期.
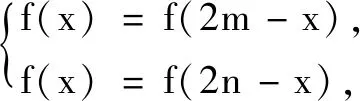
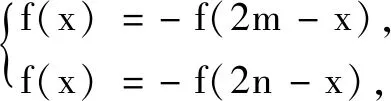
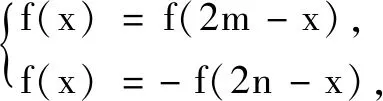
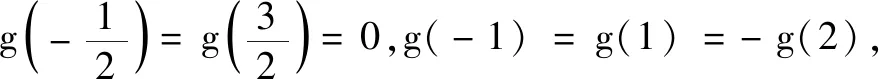
在高考中學生能否將“本手”運用自如,取決于教師平時的教學活動中是否立足于四基,即引導學生理解基礎知識、習得基本技能、感悟基本思想、積累基本活動經驗.但僅憑此,只能判斷選項BCD的正確性,作為多選題,只能得到2分,而無法得到滿分.選項A需要由f′(x)的對稱性得到f(x)的對稱性,難免會讓人根據結論2逆向猜測:若f′(x)關于x=m對稱,則f(x)關于(m,0)對稱.這樣的猜想看似合情合理,卻不免落入“俗手”.
3 俗手
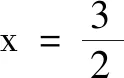
結論4若f′(x)關于x=m對稱,則f(x)關于(m,f(m))對稱;若f′(x)關于(m,0)對稱,則f(x)關于x=m對稱.
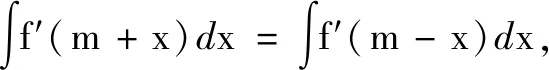
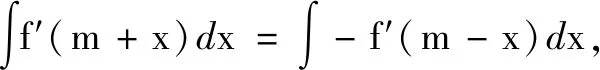
由結論4及g(x)關于x=2對稱,可得f(x)關于(2,f(2))對稱,然而f(2)的具體值無法得到,因此f(0)的值也無從得知.既然選項A的本質涉及不定積分,那么高考卷是否有超綱之嫌?筆者不以為然,不定積分可以認為是求導的逆過程,只要對原函數與導函數之間的聯系有深入的理解,也能基于高中階段的知識體系作出正確的逆向推導.
選項A是多選題中干擾項常見的設置方式,文獻[2]稱此種干擾項的類型為思維定式(熟悉的內容、相似的形式,常會令人產生類比聯想,可能產生負遷移,由此導致錯誤),筆者認為此類型的干擾項能對學生的辯證思維和深度思考能力進行有效甄別,作為多選題的最后一題,能起到較好的選拔區分功能.
可見僅僅浮于問題表面,缺乏對知識本源的深度理解和辯證思考而作出的類比遷移往往是無本之末,在多選題的得分機制中,是會導致學生錯失2分而得0分的一招“俗手”.
4 妙手
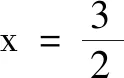
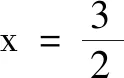
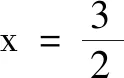
通過構造上面兩例函數,能夠立即識破選項A,不失為一招“妙手”.但筆者認為“妙手非偶得,本立而道生”,妙手的出現是基于對本手的深刻理解,取決于學生對不同類型的函數所對應的性質的認識程度.筆者發現,新高考實施以來,在其他題型中也頻現需要答卷人根據函數性質來構造具體函數的開放型問題,以下是兩個具體實例.
例1(2021年“八省聯考”第15題)寫出一個最小正周期為2的奇函數f(x)=.
例2(2021年全國新高考Ⅱ卷第14題)寫出一個具有下列性質①②③的函數f(x)=.①f(x1x2)=f(x1)f(x2);②當x∈(0,+∞)時,f′(x)>0;③f′(x)是奇函數.
可見新高考下,出卷人越來越注重考查學生依據函數性質來構造函數的能力,其背后考查的是學生的發散性思維和創新性能力.
5 結束語
2022年高考學生普遍反映新高考數學I卷難度較高,凸顯出學生對新高考考試方位和命題思路的不適應,反映出教考銜接環節的不匹配性.新高考下,高考試題更注重對思維品質的考查,強調獨立思考和創新意識;更加注重對關鍵能力的考查,強調發揮數學學科的選拔功能.以往一味的題海戰術已然失效,在知識生成過程中,教師應留給學生足夠的自由思考空間,培養學生思維的靈活性與創新性.在解題教學過程中,教師應注重數學學科的本性原法,促使學生將知識和方法內化為自身的知識結構,以此才能促使學生在高考考場上,規避“俗手”,下穩“本手”,巧施“妙手”.

