高維宇稱-時間對稱系統中的信息恢復與臨界性*

曲登科 范毅 薛鵬

1) (東南大學物理學院，南京 211189)

2) (北京計算科學研究中心，北京 100084)

3) (中國人民解放軍陸軍步兵學院，石家莊 050083)

1 引言

量子力學要求封閉系統的物理可觀測值由具有實特征值的厄密算子表示.然而在自然界中，由于耗散現象的普遍存在，不可避免地存在能量、粒子以及信息等物理量的丟失，物理量的守恒性會被破壞.因此真實的物理系統實際上是非厄米系統.近年來，非厄米系統及其動力學特性越來越受到人們的關注[1-20].研究量子系統與環境之間的相互作用是至關重要的，此相互作用可以導致耗散、衰退和退相干等現象.值得一提的是如果系統滿足宇稱-時間對稱性，則一類非厄米哈密頓量可以具有完全為實數的本征能量[21-23].非厄米哈密頓量的本征能量為實數的一個充分條件是哈密頓量滿足宇稱時間對稱性，并且哈密頓量的本征函數同時是宇稱-時間對稱算子的本征函數.滿足宇稱-時間對稱性的非厄米系統包含兩個相區域:宇稱-時間對稱性保持的區域，在此區域內整個本征譜都為實數，在宇稱-時間對稱性破壞的區域本征值形成復共軛對的形態.在這兩個相區間存在著奇異點，在奇異點處會有非常規的相變發生[24].

在增益和損耗平衡的經典系統已經預測和觀察到宇稱-時間對稱系統的幾個獨特的性質[25-32].自從第一次在光學系統中觀測到宇稱-時間對稱性破壞和功率振蕩[25，26]以來，研究人員相繼報道了非守恒系統中獨有的豐富的波的現象，如單向性[30]和多功能設備中的光傳輸[27].相關現象已經在物理學的其他子領域進行了研究，包括電路[28]和機械振蕩器[29].在量子體系中，同樣研究了宇稱-時間對稱系統的各個方面[33-43]，如玻色-哈伯德二聚體[33]、糾纏[34]以及臨界現象[39-42].

雖然損耗通常被認為會對系統的相干性產生損壞[44，45]，但是滿足宇稱-時間對稱性的經典系統中的獨特的現象和有用的應用說明了平衡增益和損耗的作用.從經典系統的研究成果來看，滿足宇稱-時間對稱性的量子系統有望顯示出對退相干的魯棒性，可能會導致量子信息處理中的長相干時間.近年來，滿足宇稱-時間對稱性的系統的信息論表征開始被探索[40-42，46].除了實際的重要性之外，這種信息論表征對于更深入地理解宇稱-時間對稱系統可以作為開放量子系統是必備的.在開放量子系統中宇稱-時間對稱的非幺正動力學的一個典型的例子就是系統與環境之間信息流動的可逆-不可逆的臨界性[46].

在2019 年，中國和日本的研究小組利用兩能級的光學系統，借助量子態間的可區分性量化信息的流動，實驗上驗證了當系統處于宇稱-時間對稱相區域時，流入環境的信息可以完全恢復[40].當系統自發破壞宇稱-時間對稱性時，信息的流動是不可逆的.同時，在宇稱-時間轉變點周圍信息的流動具有獨特的臨界性，通過該點時，可逆的信息變得不可逆，反之亦然.然而對于宇稱-時間對稱系統的量子信息的可逆性的學習目前還限于二維希爾伯特空間的系統中，在本文中，將重點介紹在高維希爾伯特空間中，在宇稱-時間對稱性保持的相區域，損失到環境中的信息仍然可以完全恢復，在靠近奇異點區域時，量子態間的可區分性會出現冪律的行為.我們使用量子態間的可區分性這一物理量統一量化了低維與高維量子系統與環境之間的信息流動.

宇稱-時間對稱系統中的信息恢復為更好地控制量子系統的行為提出了新的可能性，其方式不同于量子芝諾效應[47-49]或動態解耦[50-52].動態解耦依賴于脈沖注入的時間反轉，而本文中的信息恢復是有對稱性保護的隱藏的糾纏伙伴引起的.這其中潛在的物理本質上不同于無退相干的子空間，在無退相干的子空間中，幺正態的演化由一定的對稱性保持[53-59];相比之下，在宇稱時間對稱性保持與破壞的相區域，宇稱-時間對稱的動力學過程本質上都是非幺正的.本文第2 節會介紹信息流動的定義.第3 節回顧兩維希爾伯特空間中信息流動的恢復與臨界性.第4 節介紹高維希爾伯特空間中使用量子態間的可區分性來衡量信息的流動.最后對全文進行總結與展望.

2 信息流動

控制的動力學可以由下式表示[60]:

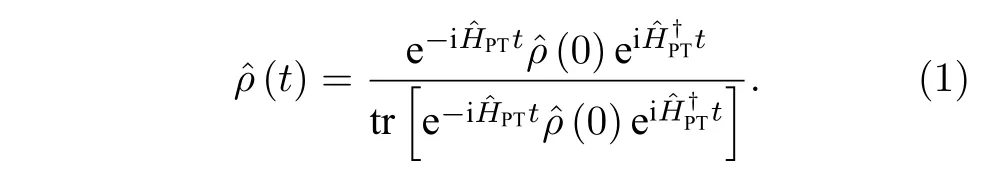
這里，通常使用希爾伯特-施密特內積.考慮一個通用的N能級量子系統，并根據同一系統的兩個量子態之間的跡距離來表征進出系統的信息流動[61]:

馬爾可夫演化問題的主要解決方法是可以基于可除性[66，69，74，75]、態的可區分性[67]、量子糾纏[69]、量子費舍爾信息流動[76]、保真度[76]、互信息[70，77]、幾何表征[78]等物理量.但并不是所有的物理量都可以很好地量化表示宇稱-時間對稱的動力學，由于非線性的原因，可除性等物理量就無法探測宇稱-時間對稱系統的動力學的非馬爾可夫性.然而，量子態之間的可區分性仍然可以作為宇稱-時間動力學中的非馬爾可夫性的一種度量，因為這種度量可以直接量化系統與環境之間的信息流動，從而檢測記憶效應的存在，即使動力學是非線性的.雖然采取其他的測量方法也是可行的，由于跡距離區分了所有不同的量子態，并且只取決于系統的動力學，因此跡距離非常適合作為信息流動的測量方法.

非馬爾可夫性起源于本征態的非正交性.為了解釋這個，對(1)式表示的宇稱-時間對稱的動力學進行本征分解:

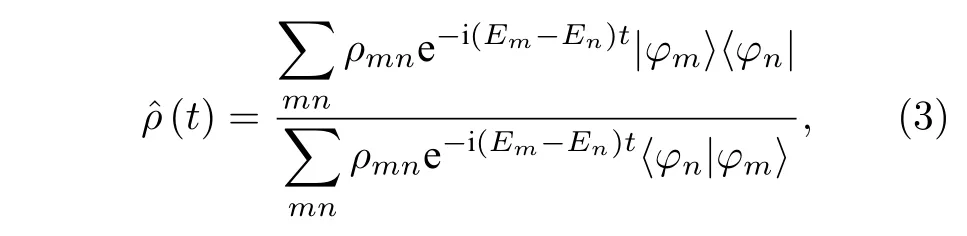
其中，|φn〉是本征能量為En的右本征矢.當動力學過程是幺正過程時，本征態是相互正交的，由(3)式的分母給出的歸一化因子始終是一個常數.在宇稱-時間對稱的動力學過程中，歸一化因子由于本征態的非正交性而振蕩，表明系統與環境之間存在連續的信息交換.在這一方面，在各種系統中觀測到的功率振蕩可以解釋為信息從環境中回流的證據[25-28，44]，以及在宇稱-時間對稱性保持的相區域的非馬爾可夫特征.

3 二能級系統中的信息恢復

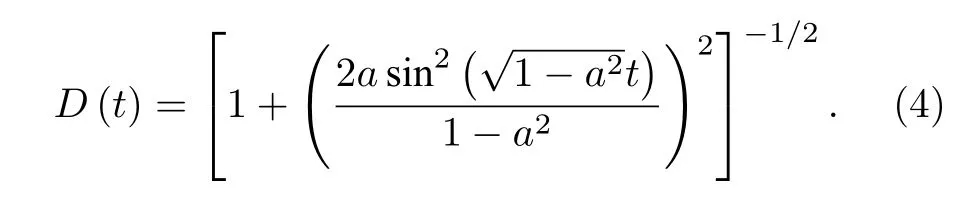
值得一提的是，在量子系統中使用單光子實現宇稱-時間對稱的動力學演化的難度在于無法實現單光子的增益.已有實驗通過更少損失與更多損失的交替來替代宇稱-時間對稱動力學中的增益與損失，從而實現了滿足宇稱-時間對稱的量子系統的動力學演化過程[37].基于這種思路，該二能級系統的哈密頓量對應的有效非厄米的哈密頓量可以寫為

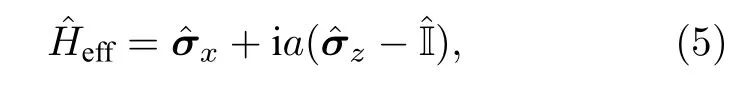
圖1(a)和圖1(b)給出了在宇稱-時間對稱的區域(0＜a ＜1)量子態之間的可區分性隨時間的演化.作為對比，也給出了幺正演化(a=0)的情況.從圖中可以看出，量子態間的可區分性隨時間會出現一個周期性振蕩的現象.這也意味著存在一段時間區域，在此時間中量子態間的可區分性的一次導數是大于 0 的.因此，系統恢復了流入環境的信息，在宇稱-時間保持的相區域展示了獨特的非馬爾可夫行為.并且從圖1(a)和圖1(b)可以看出，振蕩的時間周期隨著系統逐漸靠近奇異點的位置也逐漸上升.

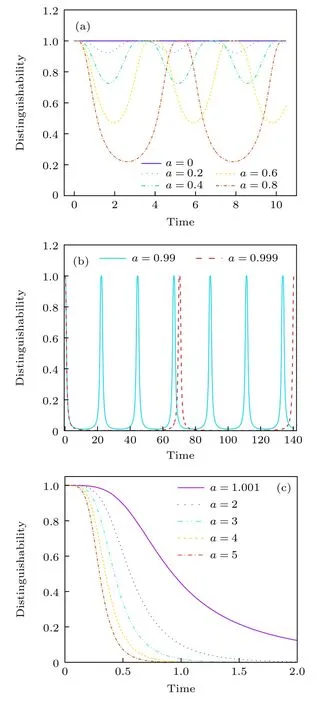
圖1 在宇稱-時間對稱的兩能級系統的信息流動 (a)，(b) 在宇稱-時 間對稱保持的區域(0 ＜a ＜1)，量子態的可區 分性表現出周期性振蕩，當逐漸靠近奇異點(a=1)時，信息恢復的周期會變長;(c) 在宇稱-時間對稱性被破壞的區域(a ＞1)，量子態的可區分性在一直在衰減Fig.1.Information flow in the parity-time-symmetric twolevel system:(a)，(b) The distinguishability oscillates with period in the parity-time-unbroken phase (0 ＜a ＜1).When approaching the exceptional point (a=1)，the period of the information retrieval.(c) The distinguishability between quantum states is declining in the parity-time-symmetry-broken regime (a ＞1).

圖1(c)給出了在宇稱-時間對稱性被破壞的相區域(a＞1)的量子態間的可區分性隨著時間的演化.可以看出，可區分性隨時間呈現指數衰減的趨勢.若使用函數D(t)=D(0)e-t/τ對數據進行擬合，其中D(0) 為常數，τ為弛豫時間，可以發現弛豫時間隨著系統接近奇異點而增加[40].在奇異點的位置(a=1)，可區分性在長時間限制內可以表現出冪律的行為.如圖2 所示，將計算的數據使用函數xt-y進行擬合，可以得到量子態間的可區分性展示出的冪律行為是D(t)～t-2，這與解析結果是完全符合的[46].

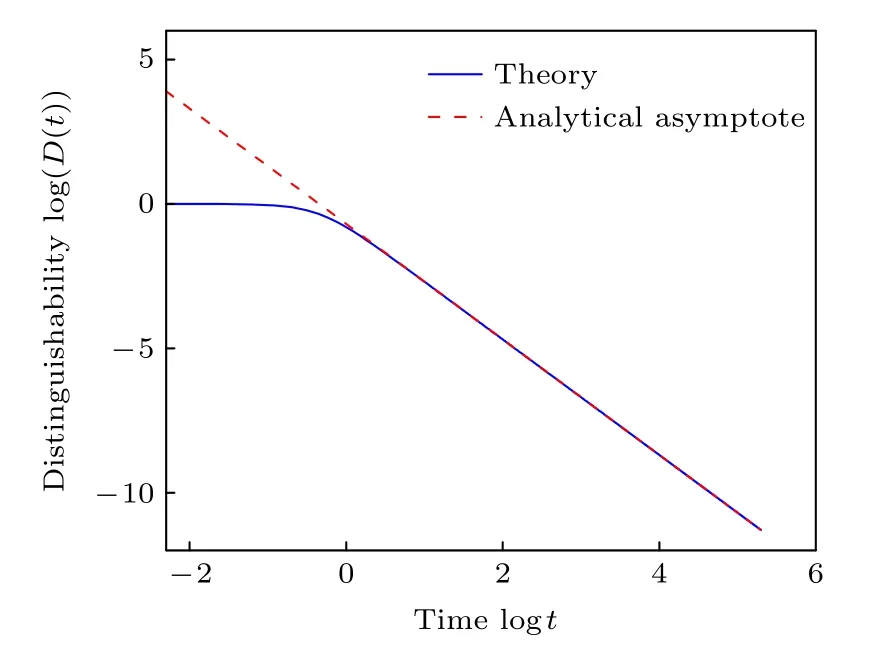
圖2 在宇稱-時間對稱的兩能級系統在奇異點處(a=1)，量子態的可區分性的冪律行為Fig.2.Power-law behavior of the distinguishability of the parity-time-symmetric system at the exceptional point a=1 .

4 四能級系統中的信息恢復

對于滿足宇稱-時間對稱性的系統的研究，還大多停留在二維希爾伯特空間中.本節主要介紹在四維希爾伯特空間中宇稱-時間對稱的動力學的信息恢復.考慮一個四能級的宇稱-時間對稱系統[41，80-82]，其由以下哈密頓量描述:

其中和為SU(2)群的自旋— 3/2 表示.該哈密頓量寫成矩陣表示為

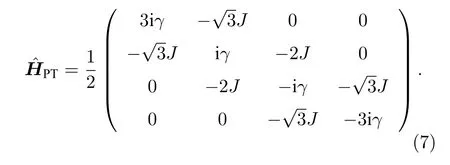
該四能級系統的基態為計算基 {|1〉，|2〉，|3〉，|4〉}.該哈密頓量與反線性的宇稱-時間算符對易，其中宇稱算符為antidiag(1，1，1，1) 且時間反演算符由它的復共軛給出.(7)式中前兩個計算模代表增益，后兩個計算模代表損失.宇稱-時間對稱哈密頓量的本征能 量可以 表示為λk={-3/2，-1/2，+1/2，，(k=1，2，3，4)，在γ=J的位置產生四階奇異點，表示有 4 個本征值與 4 個本征態都是簡并的.該宇稱-時間對稱的哈密頓量的能量間隙為，因此在γ＜J時，系統位于宇稱-時間對稱性保持的相區域，在γ＞J時，系統的宇稱-時間對稱性被打破.為了衡量在四能級系統中 的信息流動，選擇初 態ρ1=1/2(|1〉+|2〉)(〈1|+〈2|) 和ρ2=1/2(|3〉+|4〉)(〈3|+〈4|) .依 然可以通過通過(2)式計算兩個態隨時間演化的可區分性.

如圖3(a)和圖3(b)所示，選擇參數J=1，對于系統處于幺正演化的情況(γ=0)，量子態之間的可區分性始終為 1，也就意味著系統的信息沒有流失.在宇稱-時間對稱性保持的相區域(γ＜J)，與二能級系統中展示的宇稱-時間對稱的動力學過程相同，量子態之間的可區分性呈現出周期性振蕩的現象，這種現象也標志著系統流入環境的信息會完全恢復.隨著系統逐漸逼近奇異點，振蕩的周期也是逐漸變長，并且信息恢復的程度也在變大.圖3(c)表示量子態之間的可區分性隨著時間的增加一直在衰減.當接近奇異點時，量子態的可區分性漸進地表現為D～1/t2.如圖4 所示，在奇異點的位置(γ=J)，量子態之間的可區分性在長時間的演化后表現出冪律行為.將計算結果使用函數xt-y進行擬合，可以得到在奇異點處，量子態的可區分性表現出的冪律行為是D～1/t2.

圖3 宇稱-時間對稱的四能級系統的信息流動 (a)，(b) 在宇稱-時間對稱保持的區域(γ ＜J)，量子態的可區分性表現出周期 性振蕩，當逐漸靠近奇 異點(γ=J)時，信 息恢復的周期會變長;(c) 在宇稱-時間對稱性被破壞的區域(γ ＞J)，量子態的可區分性在一直在衰減Fig.3.Information flow in the parity-time-symmetric fourlevel system:(a)，(b) The distinguishability oscillates with period in the parity-time-unbroken phase (γ ＜J).When approaching the exceptional point (γ=J)，the period of the information retrieval.(c) The distinguishability between quantum states is declining in the parity-time-symmetrybroken regime (γ ＞J).

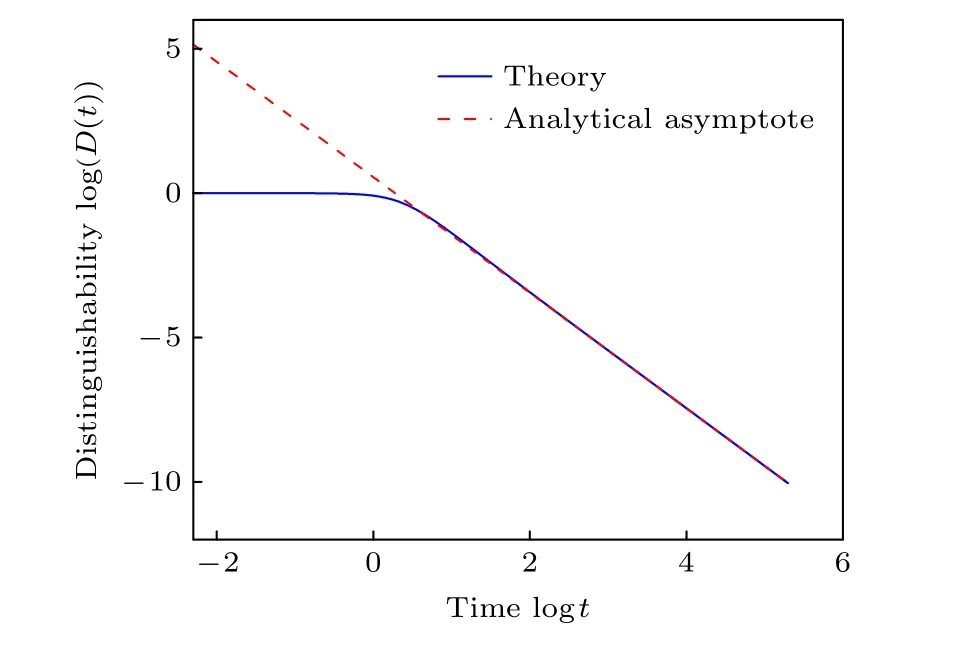
圖4 在宇稱-時間對稱的四能級系統在奇異點處(γ=J)，量子態的可區分性的冪律行為.Fig.4.Power-law behavior of the distinguishability of the parity-time-symmetric system at the exceptional point γ=J .

由于線性增益放大器中噪聲的量子限制[83]，不可能在量子領域中創建具有平衡增益和損失的量子系統[84].奇異點的簡并現象也可以在具有模式選擇損失的耗散系統中實現.這種被動的宇稱-時間對稱系統已經在量子領域實現，如單光子[85-88]、超冷原子[36]、超導傳輸子[89].基于以上基礎，針對本文提出的高維希爾伯特空間中的信息恢復與臨界性的方案，也可以借助單光子光源去實現耗散系統[90-96]，從而觀測到宇稱-時間對稱動力學演化的臨界現象.

5 總結和展望

高維的宇稱-時間對稱系統可以視為兩個或者多個最小的非厄米量子系統的組合，為宇稱-時間對稱性與奇異點簡并性的相互作用的量子模型提供了一個新的起點.本文發現流入環境中的信息可以在高維的宇稱-時間對稱系統中恢復.在非厄米動力學過程中，奇異點扮演著臨界點的角色，當系統穿越該點時，信息流動的可逆性變為不可逆，反之亦然.在臨界點的周圍，量子態間的可區分性這一物理量表現出冪律行為.并且使用量子態的可區分性統一量化了低維與高維宇稱-時間對稱系統中的信息流動.這些發現可能在量子控制中找到新的應用.