基于高維單粒子態的雙向半量子安全直接通信協議*

龔黎華 陳振泳 徐良超 周南潤

(南昌大學電子信息工程系，南昌 330031)

1 引言

量子通信協議主要包括量子隱形傳態 (quantum teleportation)[1-3]、量子密鑰分配(quantum key distribution，QKD)[4-6]、量子簽名[7，8]、量子身份認證(quantum identity authentication，QIA)[9]、量子秘密比較(quantum private comparison，QPC)[10，11]以及量子安全直接通信(quantum secure direct communication，QSDC) 等.近年量子芯片[12，13]的快速發展，有助于降低量子通信的成本.

量子安全直接通信在量子信息技術中扮演著重要的角色.不同于量子密鑰分配傳輸隨機數，量子安全直接通信無需密鑰，可以利用量子信道直接傳輸秘密信息.2002 年，Long 和Liu[14]利用Einstein-Podolsky-Rosen (EPR)態的糾纏特性，設計了第一個量子安全直接通信協議，Bostr?m 和Felbinger[15]基于EPR 對的糾纏特性提出了著名的乒乓協議(ping-pong protocol，PPP).2003 年，以EPR 對為信息載體，Deng 等[16]提出了一個“兩步”QSDC 協議.2004 年，Deng 和Long[17]基于量子一次一密技術設計了一個QSDC 協議.2005 年，Wang 等[18]基于高維量子超密編碼構建了一個QSDC 協議.2011 年，Shi 等[19]利用三維超糾纏性質設計了一個QSDC 協議.2017 年，Zheng 和Long[20]基于Cluster態提出了一個信道容量可控的QSDC 方案.2018年，Chen 等[21]利用Bell 態的超糾纏特性構建了一個“三步”三方QSDC 協議.2019 年，Gao 等[22]提出了測量設備無關的遠程QSDC 協議.2020 年，Zhou等[23]提出了與設備無關的QSDC 協議.2022 年，利用Bell 態的超糾纏特性，Sheng 等[24]構建了一個“一步”QSDC 協議.QSDC 的物理可實現性逐漸被實驗所驗證.2016 年，Hu 等[25]實現了基于單光子的QSDC 實驗.2017 年，Zhang 等[26]借助量子寄存器實驗實現了“兩步”QSDC 協議，同年，Zhu等[27]實現了長距離QSDC 實驗.2021 年，Qi 等[28]實現了15 個用戶之間的QSDC 網絡.

通常，量子通信協議要求每一位參與者都具備完整的量子能力，即參與者具備在量子比特或量子系統上進行量子操作的全部能力.然而，并不是每位參與者都能負擔的起昂貴的量子設備.Boyer 等[29]最早提出了半量子的概念，半量子意味著量子方擁有完整的量子能力，而經典方不需具備完整的量子能力，或者說經典方只能用一組固定的基{|0〉，|1〉}處理量子信息.Zhou 等[30]指出半量子也可以保證量子中心與無量子能力的用戶之間的通信安全.半量子技術在量子通信的各個方向上都得到了應用，例如:半量子密鑰分配(semi-quantum key distribution，SQKD)[31，32]、半量子身份認證(semi-quantum identity authentication，SQIA)[33]、半量子秘密比較(semi-quantum private comparison，SQPC)[34，35]以及半量子安全直接通信(semi-quantum secure direct communication，SQSDC)等.

半量子安全直接通信結合量子安全直接通信和半量子的思想，為資源受限的經典方和具備完整量子能力的量子方之間提供了直接傳輸秘密信息的可靠方式.SQSDC 的提出不僅有利于提高量子通信協議的可實現性，而且有利于減少量子通信中設備資源的消耗.

2014 年，Zou 等[36]討論了半量子安全直接通信，結合一次一密技術提出了一個基于單光子的“三步”SQSDC 協議.隨后，Gu 等[37]對該“三步”SQSDC 協議進行改進，設計了一個可以抵御雙重C-NOT 攻擊的SQSDC 協議.2017 年，Zhang 等[38]利用EPR 對的糾纏特性和誘騙態思想，提出了一個全新的SQSDC 協議.2018 年，Xie 等[39]將量子方和經典方的職責互換，以 Bell 態為信息載體設計了一個信息發送者為量子方的SQSDC 協議.2019 年，Sun 等[40]通過引入新的編碼手段提出了兩個基于Bell 態的高效SQSDC 協議.2020 年，Rong等[41]利用Bell 態糾纏特性，設計了一種多參與方的SQSDC 協議.

然而，現有的半量子安全直接通信協議只使用二維量子態作為信息的載體，并要求經典方具備量子態測量能力.為了突破低維量子態的限制，提高信息傳輸效率、減少量子資源的消耗和降低協議的實現難度，本文基于高維單粒子態設計了一個雙向SQSDC 協議.

2 高維單粒子態

d維量子系統中的Z基和X基的定義和分別為

其中⊕為模d加.Ye 等[42]指出當對Z基粒子|k〉執行幺正操作Um時，它的量子態將會變成|k ⊕m〉，而當對基粒子進行幺正操作Um時其狀態不會改變.

3 協議描述

在無噪聲、無失真的理想環境中，擁有完整量子能力的量子方Alice 和能力受限的經典方Bob(無需具備量子態測量能力)之間基于高維單粒子態的雙向半量子安全直接通信協議的具體步驟如下:

步驟1Alice 隨機制 備 4n個Z基粒子 和n個基粒子，n為Alice 和Bob 在一次通信過程中需傳輸的秘密信息長度.Alice 將X基粒子隨機插入基粒子序列中得到序列ST，并將其發送給Bob.

步驟2Bob 收到序列ST后，對粒子隨機執行CTRL 或幺正操作Um并記錄m的值得到序列ST1.Bob 通過不同的延時線對所有粒子進行重新排序得到序列，并將其返還Alice.根據粒子的原始狀態和Bob 的操作，可將所得的粒子歸為四類，如表1 所列.

表1 操作后粒子的分類Table 1.Classification of the particles after operation.

步驟3Alice 收到序列后，公布原始序列中基粒子的位置.Bob 公布序列的正確順序和對每個粒子執行的操作，并隨機公布一半對基粒子執行的幺正操作信息.Alice 恢復粒子序列的正確順序，并按照粒子發送時的基測量粒子，結果如表2 所列.Alice 比對每個收到粒子的測量結果和預期結果，計算誤碼率.若誤碼率高于預設的閾值，則說明竊聽存在，終止本次協議，否則Alice 將剩余未公布幺正操作的-U粒子作為媒介粒子(媒介粒子組成的序列記為Sm)，并通過比對測量結果讀出媒介粒子Sm的幺正操作信息m.

表2 Alice 的竊聽檢測策略Table 2.Eavesdropping detection strategy for Alice.

步驟4根據自己的秘密信息ma和Bob 的幺正操作信息m，Alice 計算Ma=m ⊕ma.Alice根據Ma制備n個基粒子得到序列SC，并將之發送給Bob.

步驟5根據自己的秘密信息mb和幺正操作信息m，Bob 計算Mb=m ⊕mb.在收到序列SC后，Bob 根據Mb對粒子執行幺正操作UMb得到序列SC1，并將其返還Alice.

步驟6Alice 收到序列SC1后，用基對其進行測量，并公布測量結果M=Ma⊕Mb.

步驟7根據測量結果M=Ma⊕mb⊕m(M=Mb⊕ma⊕m)，Alice (Bob)獲得Bob (Alice)的秘密信息mb=M ?Ma?m(ma=M ?Mb?m)，其中?為模d減.

步驟8Alice(Bob)利用哈希函數h() 分別計算出秘密信息ma(mb)的哈希值h(ma) (h(mb))和收到秘 密信息()的哈希值h() (h()).Alice 和Bob 分別公布自己秘密信息的哈希值.如果h()=h(mb) (h()=h(ma))，則Alice(Bob)收到的秘密信息準確無誤.否則，收到的秘密信息有誤，Alice 和Bob 將丟棄收到的秘密信息并重新執行協議.

4 安全性分析

4.1 截獲重發攻擊

Eve 截獲并用提前制備的欺詐粒子替換Alice發送給Bob 的每個粒子，并在Bob 將粒子返回給Alice 時再次截獲粒子.通過測量欺詐粒子并比對測量結果與欺詐粒子的原始狀態，Eve 試圖獲取Bob 的操作信息，并通過執行與Bob 相同的操作以竊聽秘密信息.在截獲重發攻擊中，Eve 可以選擇Z基粒子或基粒子作為欺詐粒子，具體情況如下:

1) Eve 選擇基粒子作為欺詐粒子

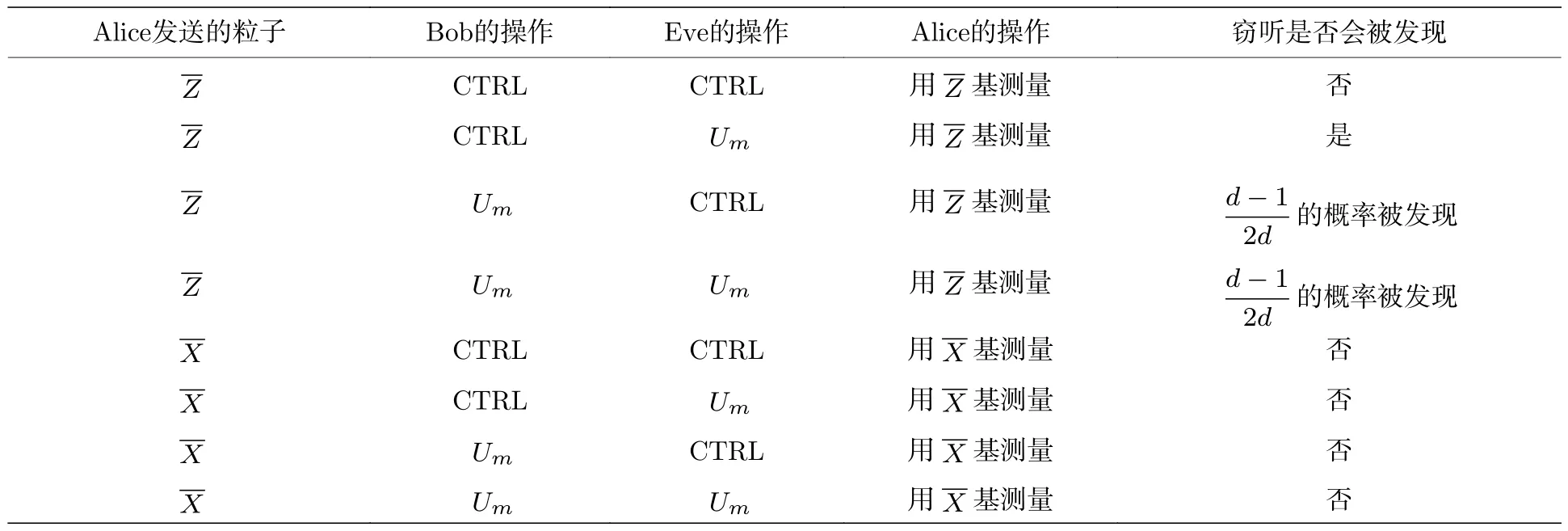
表3 Eve 的截獲重發攻擊Table 3.Intercept-resend attack by Eve.

2) Eve 選擇基粒子作為欺詐粒子

在截獲Alice 傳來的粒子后，Eve 將提前制備的基粒子發送給Bob.Bob 對收到的粒子只能執行CTRL 或幺正操作Um.這兩種操作都無法改變基粒子的狀態.當Eve 對返回的基粒子進行基測量時，所有基粒子都維持原始狀態.Eve無法從中獲得Bob 的操作信息，只能對截獲的粒子進行隨機操作并將其返還Alice.這會增大誤碼率進而被Alice 發現.

4.2 測量重發攻擊

在測量重發攻擊中，Eve 截獲并測量每一個由Alice 發送給Bob 的粒子，并制備與測量結果相同狀態的新粒子發送給Bob.在Bob 將粒子返回給Alice 時，Eve 再次截獲并用與之前相同的基測量粒子，試圖獲取秘密信息.在發送基粒子時，Alice在其中混入了基粒子作為誘騙態，因此Eve 在對截獲的粒子進行測量時，必須使用和兩種測量基測量粒子.然而，Eve 無法準確區分每個粒子所屬的基，只能隨機選擇測量基.當測量基與Alice發送的粒子不匹配時，Eve 的竊聽行為將大概率被Alice 發現.為了更清晰地展示Eve 的攻擊對整個通信過程的影響，表4 列出了竊聽者和合法參與者在執行不同操作后產生的結果.

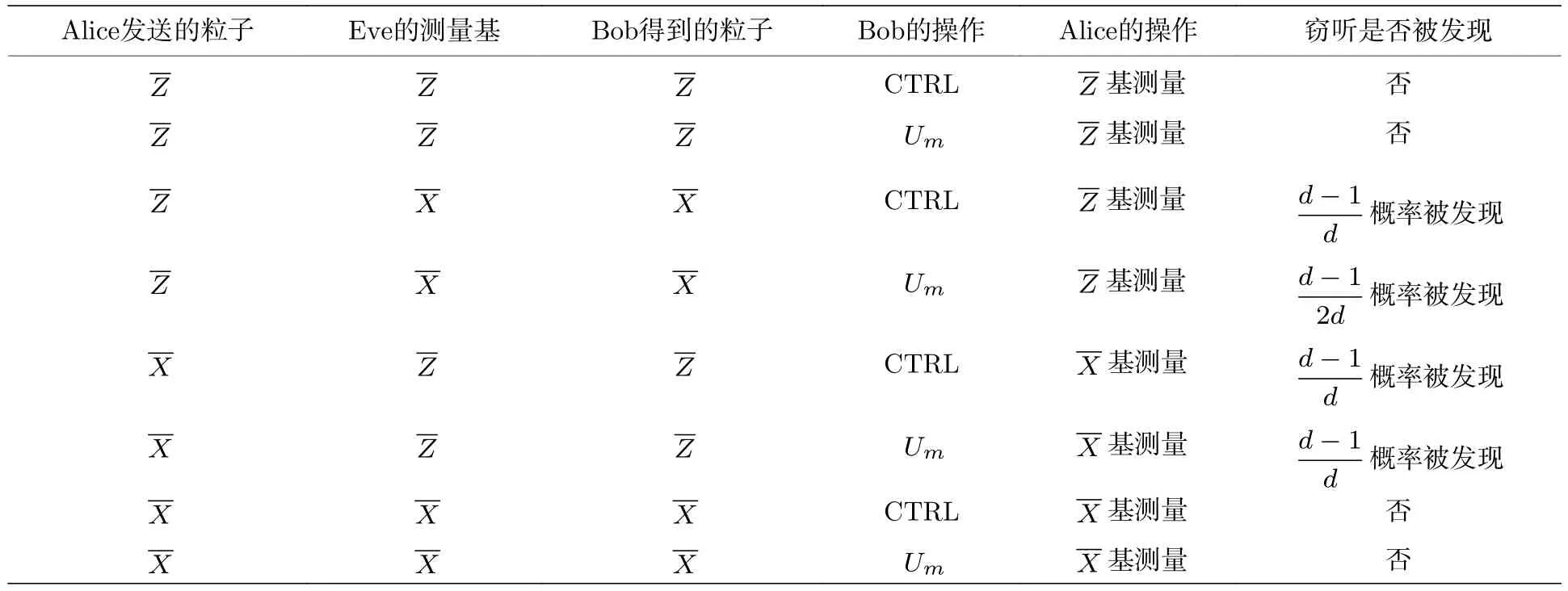
表4 Eve 的測量重發攻擊Table 4.Measurement-resend attack by Eve.

1) Alice 發送的 是基粒子 而Eve 選擇基進行測量

Eve 選擇的測量基與Alice 發送粒子的基相同，且Bob 的操作不會改變粒子的基.當Alice 測量返回的粒子時，無法發現Eve 的竊聽.

Eve 的基測量使得Alice 發送的粒子坍縮為基粒子.Bob 的操作不會改變粒子的基，因此返回給Alice 的粒子仍然為基.當Bob 選擇執行CTRL 操作時，Alice 將以概率 (d-1)/d發現Eve的竊聽.當Bob 選擇執行幺正操作Um時，因為Bob 只公布一半的-U粒子，Alice 將以概率(d-1)/2d發現Eve 的竊聽.

Eve 的基測量使得Alice 發送的粒子坍縮為基粒子.Bob 的操作不會改變粒子的基，因此返回給Alice 的粒子仍然為基.Alice 將以概率(d-1)/d發現Eve 的竊聽.

Eve 選擇的測量基與Alice 發送粒子的基相同，且Bob 的操作不會改變粒子的基.當Alice 對返回的粒子進行測量時，無法發現Eve 的竊聽.

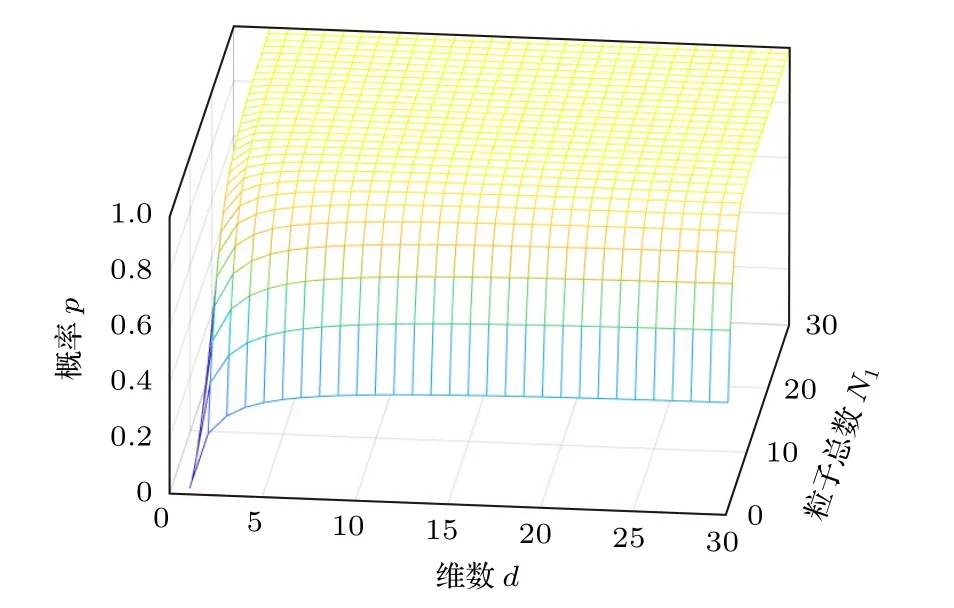
圖1 竊聽檢測概率Fig.1.Eavesdropping detection probability.

4.3 糾纏測量攻擊

Eve 在Alice 發送粒子給Bob 時，對每一粒子執行幺正操作UE，將制備的輔助粒子|ε〉與Alice的粒子糾纏在一起，測量輔助粒子可以提取有用信息.當Eve 對基粒子執行幺正操作UE時可得

Bob 的兩個操作都無法改變基粒子的狀態，基粒子在Eve 執行UE和UG后可以表示為

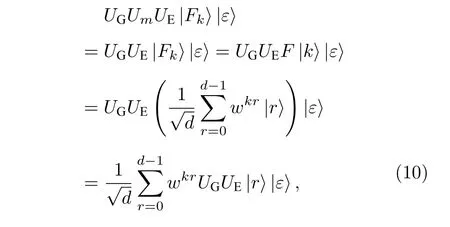
結合(9)式和(10)式可得

F-1為量子傅里葉逆變換.為了避免被Alice 發現，Eve 必須使Alice 的測量結果與發送的粒子態相同，即|Fy〉 必須等于|Fk〉 .由此可得

由(11)式及(12)式，可得

由(13)式可知，Eve 無法區分輔助態|ε00〉，|ε11〉，···，|εd-1，d-1〉，即無法獲得Alice 和Bob 的秘密信息.因此，本協議可以抵抗糾纏攻擊.

4.4 篡改攻擊

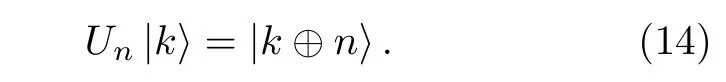
顯然，如果Bob 選擇執行CTRL 操作，Alice 會發現粒子的測量結果與預期結果不同.如果Bob 選擇執行Um操作并且公布相應的m值，Alice 的測量 結果將為|k ⊕n ⊕m〉而非預期的|k ⊕m〉.如 果Bob 選擇執行Um操作而未公布相應的m值，則被篡改的粒子將作為媒介粒子.Alice 獲取的媒介粒子信息為n⊕m將不同于Bob 的m，當協議進行到差錯檢測步驟時，Alice 通過哈希函數獲得的秘密信息檢測值將與Bob 的不同，參與者將發現秘密信息被篡改.因此，無論Eve 的篡改攻擊發生在協議中的哪一種粒子上，都無法在不被發現的情況下篡改秘密信息.因此，本協議可以抵抗篡改攻擊.

5 效率分析

量子通信協議的效率計算式為[43]

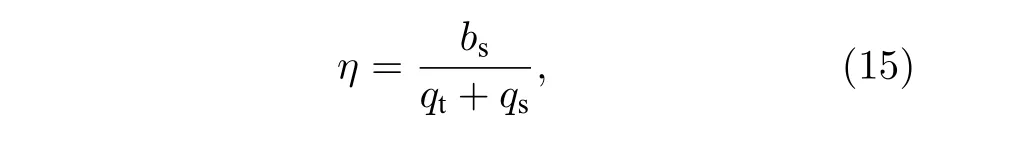
其中bs，qt，qs分別表示傳遞秘密信息的數量，協議使用的量子比特總數和協議中所需經典比特數量.本協議中Alice 共制備了 6n個d維單粒子態而Bob在整個通信進程中未制備任何量子態，即qt=6n.Alice 和Bob 在譯碼階段共使用了n個經典比特讀取彼此的秘密信息，即qs=n.在一次通信進程中，Alice 和Bob 分別向對方傳遞了n個d維單粒子態的秘密信息，即bs=2n.因此本協 議的效率 為.本協議以d維單粒子為信息的傳輸載體，每一個單粒子可以傳輸 log2d比特的秘密信息.圖2 為維數與單粒子傳輸秘密信息量的關系，易知，隨著維數d的不斷增加，單粒子可以傳輸更多的秘密信息.

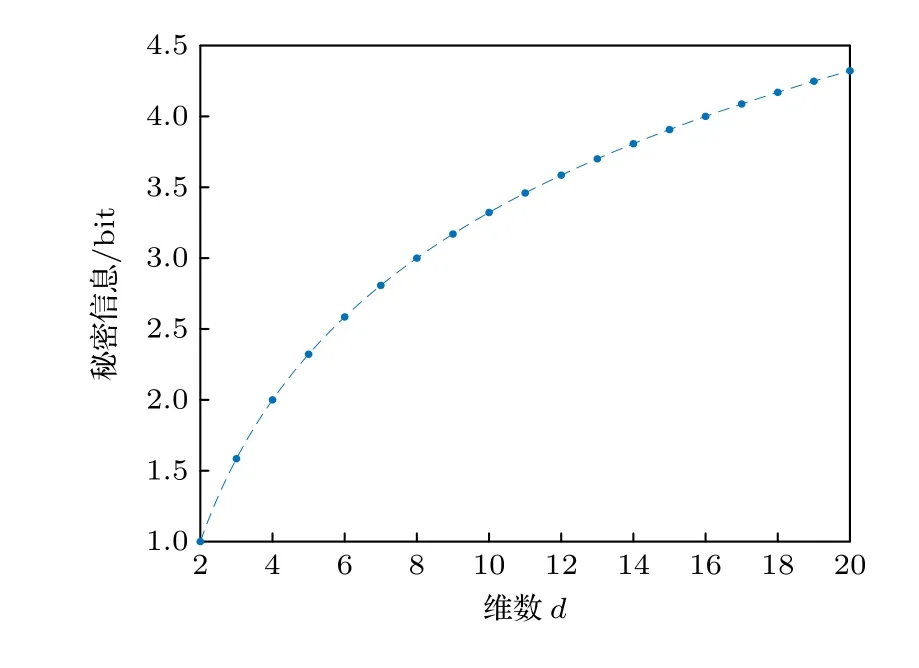
圖2 單粒子傳輸秘密信息-維數Fig.2.Single particle transport secret information -dimension.

現有的SQSDC 協議通常是基于低維單粒子態或低維糾纏態，每個粒子只能編碼1 比特的秘密信息，秘密信息的傳輸效率不高，本文首次基于高維量子態實現SQSDC 協議，當維數足夠大時，將明顯提高秘密信息的傳輸效率.現有的SQSDC 協議中一般要求經典方具備量子態測量能力，本協議中經典方無需具備量子測量能力，這降低了協議的實現難度.此外，本協議是一個雙向通信協議，在一次通信進程中兩個參與者都可以同時發送和接收秘密信息.本協議與一些現有SQSDC 協議的詳細比較如表5 所列.與現有的SQSDC 協議相比，本文協議具有更高的秘密信息傳輸效率.

表5 本協議與現有經典SQSDC 協議的比較Table 5.Comparison of the proposed protocol with existing classical SQSDC protocols.

6 總結

本文提出的基于高維單粒子態的雙向半量子安全直接通信協議中的合法參與者為量子方Alice和經典方Bob，每個參與者既是秘密信息發送方，又是秘密信息接收方.本文協議中的經典方Bob 無需具備量子態測量能力，這降低了協議對于量子設備的需求.安全性分析表明，本文協議可以抵抗測量重發攻擊、截獲重發攻擊和糾纏測量攻擊等常見攻擊手段.此外，每個d維粒子可以編碼 log2d比特的秘密信息而每個二維量子比特只能編碼1 比特的秘密信息，因此，與基于二維量子比特的單向半量子安全通信協議相比，當d足夠大時本協議具有更高的秘密信息傳輸效率.