溯本求源·發展素養
——對幾何體外接球問題的思考
◎史彬彬
(南寧市東盟中學,廣西 南寧 530105)
空間幾何體外接球球心位置的確定是解決立體幾何問題的重點和難點,要求學生具有較好的空間想象能力,并能熟練掌握空間幾何體的結構特征及位置關系的判斷方法,這也是發展學生直觀想象和邏輯推理兩個學科核心素養的重要載體.筆者從球截面的幾何性質和代數特征出發,通過對圓柱、圓錐的外接球球心位置的確定及半徑的計算,對多面體的外接球問題進行思考.
一、球截面的性質
幾何性質平面與球相交,交線為圓,且球心與截面圓圓心所在的直線垂直于截面.
代數特征如圖1,球心為O,截面圓圓心為O′,則直線OO′⊥圓O′.設球O的半徑為R,圓O′的半徑為r,|OO′|=d,則由勾股定理得R,r,d滿足R2=r2+d2.

圖1
二、圓柱的外接球
問題1記圓柱的高為h,底面圓的半徑為r,求該圓柱的外接球半徑R.


圖2
例1(2017年·全國卷Ⅲ)已知圓柱的高為1,它的兩個底面的圓周在直徑為2的同一個球面上,求該圓柱的體積.

延伸1.1如圖3,以圓柱底面圓的任意內接多邊形為底面,該多邊形的頂點對應的母線為側棱的直棱柱的外接球與該圓柱的外接球相同.

圖3
例2(2010年·課標卷)設三棱柱的側棱垂直于底面,棱長都為a,求該三棱柱外接球的表面積.
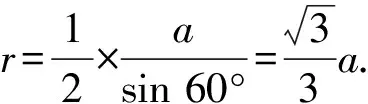
延伸1.2側棱垂直于底面,且底面多邊形存在外接圓的棱錐可補形為圓柱,該棱錐的外接球與對應圓柱的外接球相同.
例3(2021屆西南名校高三第三次聯考)如圖4,已知三棱錐P-ABC中,∠BAC=90°,∠APC=30°,平面PAC⊥平面ABC,AB=AC=4,求三棱錐P-ABC外接球的表面積.

圖4

三、長方體的外接球
問題2記長方體的長、寬、高分別為a,b,c,求該長方體外接球的半徑.
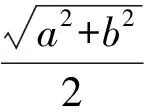
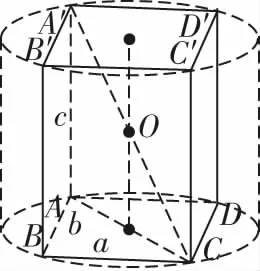
圖5
例4(2017年·全國卷Ⅱ)長方體的長、寬、高分別為3,2,1,其頂點都在球O的球面上,求球O的表面積.
解析設球O的半徑為R,則(2R)2=32+22+12=14,故表面積為14π.
延伸在長方體的八個頂點中,選取不共面的四個頂點構成一個三棱錐,則該三棱錐的外接球與長方體的外接球相同.
根據不同的取點方法,可以得到如下兩類三棱錐:①側棱垂直于底面,且底面是直角三角形的三棱錐,如圖6(1)(2);②對棱長相等的三棱錐,如圖6(4).對于圖6(3),△ABP與△ACP均是以AP為斜邊的直角三角形,則AP的中點到A,B,C,P的距離相等,由球的定義知AP為球的直徑.
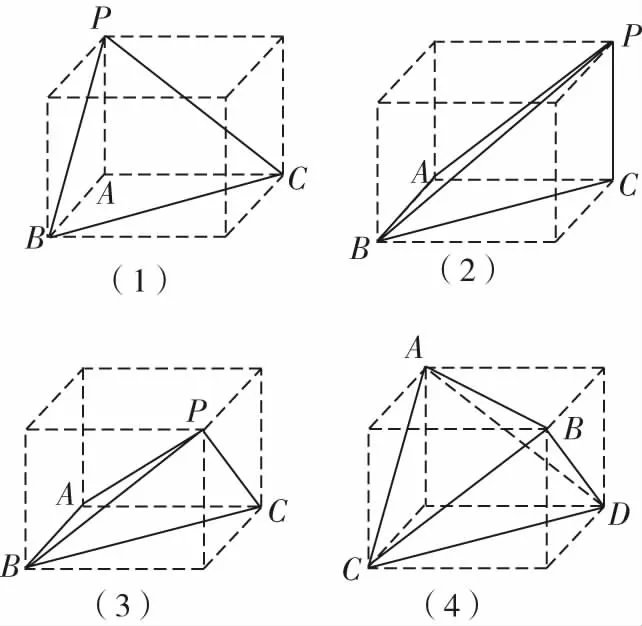
圖6
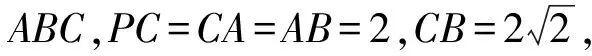
解析因為AC2+AB2=BC2,所以△ABC為以BC為斜邊的直角三角形.又因為PC⊥平面ABC,所以可補形為如圖6(2)所示的長方體.由題設知長、寬、高分別為2,2,2,所以外接球半徑R滿足(2R)2=22+22+22,即4R2=12,則表面積為12π.
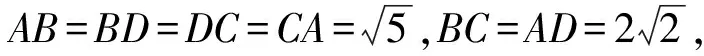

則a2+b2+c2=9,故外接球的表面積為4πR2=π(a2+b2+c2)=9π.
注長方體是特殊的直棱柱,其外接球問題可以利用圓柱模型求解.討論長方體的外接球源于兩方面的思考:(1)長方體是學生最先學習且最為熟悉的空間幾何體,是學生認識立體幾何中位置關系的重要載體.對長方體外接球球心位置的討論,有助于學生理解其他幾何體的外接球問題.(2)對棱長相等的三棱錐,不易補形成圓柱.
四、圓錐的外接球
問題3記圓錐的高為h,底面圓的半徑為r,求該圓錐外接球的半徑.
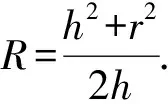
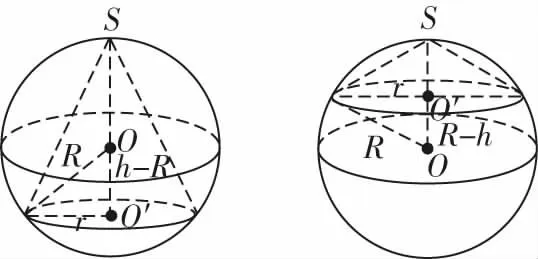
圖7

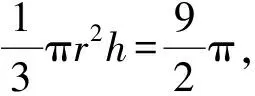
延伸如圖8,以圓錐底面圓的任意內接多邊形為底面,圓錐的頂點為頂點的棱錐的外接球與該圓錐的外接球相同.即頂點在底面內的射影為底面外接圓圓心的棱錐(側棱長相等)可補形為圓錐.

圖8
例8(2014年·全國卷)若正四棱錐的高為4,底面邊長為2,求該棱錐外接球的表面積.
五、一般多面體的外接球
對于一般多面體的外接球問題,可以考慮以下解決辦法:
思路1考慮多面體不在同一平面內的部分頂點,將問題轉化為長方體或旋轉體的外接球問題.

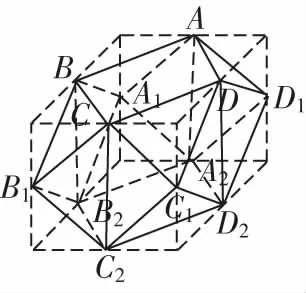
圖9

思路2類比三角形外接圓圓心位置的確定方法,確定多面體外接球的球心.
因為球心在過截面圓圓心且垂直于截面的直線上,分別過多面體相交的兩個側面的外心作平面的垂線,那么兩條垂線的交點就是該多面體外接球的球心,交點到任意頂點的距離為半徑.
例10如圖10,在邊長為4的等邊三角形ABC中,D,E分別為AB,AC的中點,將△ADE沿DE折起,使得平面ADE⊥平面BDEC,求折疊后所得四棱錐A-BDEC的外接球的表面積.

圖10
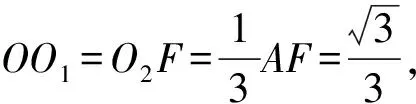
一般結論如圖11(1),記△ABC的外心為O1,△PAB的外心為O2,過O1,O2分別作平面ABC、平面PAB的垂線m,n,則直線m,n的交點即為外接球的球心O.取AB的中點為D,則O1D⊥AB,O2D⊥AB,設∠O1DO2=θ(θ為二面角P-AB-C所成平面角的大小).
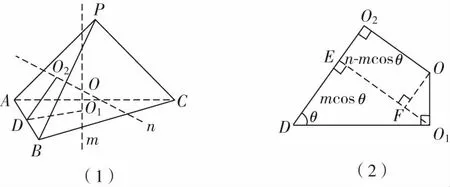
圖11
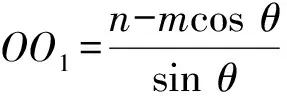
六、歸納總結
空間中,不在同一平面內的四點確定一個球.若一個多面體存在外接球,則只需在多面體的頂點中合理地選擇不在同一個平面內的四點,那么這四點所對應的外接球就是該多面體的外接球.故解決三棱錐的外接球問題是關鍵.

對于一般的三棱錐,結合題設中所給的結構特征(如面面垂直),類比三角形的外接圓,利用兩個面的“中垂線”確定球心,將立體幾何問題轉化為平面幾何問題求解即可.
七、教學建議
多面體外接球球心的確定因結構特征的不同,解決方法也不同,但其本質都是球截面性質的應用.
在教學過程中,教師可借助信息技術手段,通過“截面的性質與弦的性質、圓柱的外接球與長方形的外接圓、圓錐的外接球與等腰三角形的外接圓、三棱錐的外接球與三角形的外接圓”的類比,動態地展示平面圖形向空間圖形的轉化過程,引導學生在圓柱、圓錐兩個旋轉體外接球的基礎上對多面體的外接球進行思考,以小見大,深入挖掘,體現轉化與化歸的數學思想方法,培養學生從源頭上分析問題和解決問題的能力,促進學生直觀想象和邏輯推理等核心素養的發展.

