巧用賦值法解決高考函數零點問題
山東 劉目勇
(作者單位:山東省淄博第六中學)
函數零點存在性問題在全國卷高考題中較為常見,如果在解決這些題目時選擇參變分離就無法避免極限和數形結合的問題,這種做法在高考閱卷中肯定會出現扣分較多的情況.這是因為極限問題在高中階段屬于超綱內容,而數形結合在解答題中的運用又不太嚴謹,所以高考標準答案都是選擇分類討論、賦值然后運用零點存在性定理進行求解,這也是高中階段最嚴謹的做法.但是答案中只會告訴我們把某個點代入是成立的,但是這個點是怎么找出來的,往往會讓很多學生甚至老師都感到茫然,尤其是高考題中含參數的函數賦值就更是難上加難.常見的賦值方法有函數放縮賦值法、10 086移動取點法、分而治之取點法,其中函數放縮賦值法一般是標準答案采用的辦法,本文主要通過剖析高考題對這三種方法進行初步探討.
一、三種賦值方法的原理
1.函數放縮賦值法
比如要尋找x1使得f(x1)>0,若這樣的x1不好尋找,我們就可以通過函數放縮解不等式f(x)>g(x)≥0,其中g(x)≥0是一個易解不等式,在g(x)≥0的解集中任取一個實數作為x1即可.常見的函數放縮不等式以及階的比較如下:
(1)ex≥x+1,ex≥ex;
(2)當x>0時,ex>x2+1,ex>x2+x;
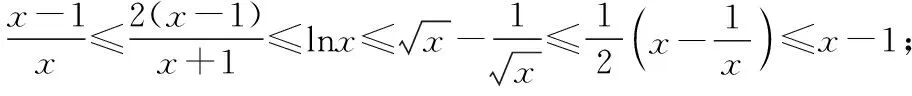
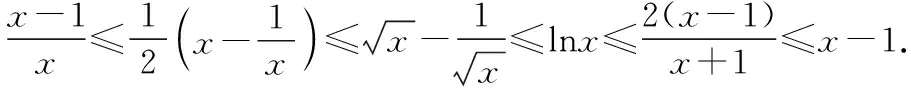
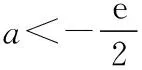
另外我們還需要知道無窮遠處無窮大函數的階的比較關系:c< 2.10 086移動取點法 3.分而治之取點法 【例1】已知函數f(x)=ae2x+(a-2)ex-x. (1)討論f(x)的單調性; (2)若f(x)有兩個零點,求a的取值范圍. 1.當0 函數放縮法:f(x)=ae2x+(a-2)ex-x>(a-2)ex-x>a-2-x≥0得x≤a-2,故 2.當0 通過上面的分析我們可以看出,如果要運用函數進行放縮,應該大膽地進行添加、刪除項或者根據函數不同的階進行放縮,把不可解方程變為可解方程.如果采用10 086移動取點法應該在許可范圍內取一個與10 086有關的點的值進行驗算,當覺得問題復雜難解的時候分而治之也是一個不錯的選擇. 有了上面的分析我們可以選取一種放縮方法對此題第(2)問進行作答. 綜上所述,f(x)有兩個零點,a的取值范圍為(0,1). 【例2】已知函數f(x)=(x-2)ex+a(x-1)2有兩個零點,求a的取值范圍. 解:f′(x)=ex+(x-2)ex+2a(x-1) =(x-1)(ex+2a). ①當a=0時,f(x)=(x-2)ex,此時f(x)只有一個零點,不符合題意, ②當a<0時,令f′(x)=(x-1)(ex+2a)=0得x=1或x=ln(-2a), 而f(1)=-e<0, f(ln(-2a)=[ln(-2a)-2](-2a)+a[ln(-2a)-1]2 =a{[ln(-2a)-2]2+1}<0, 所以x<1時f(x)<0,此時f(x)在(-∞,+∞)上最多有一個零點,不符合題意. ③當a>0時,f(x)在(-∞,1)上單調遞減,(1,+∞)上單調遞增.f(1)=-e<0,f(2)=a>0,所以f(x)在(1,2)內存在唯一的零點. 當x<1時,我們采用下面兩種方法進行找點,我們可以令x<0. 方法一(函數放縮法): 方法二(分而治之取點法和10 086移動取點法相結合): f(x)=(x-2)ex+a(x-1)2>0, 所以f(x)在(x1,1)上存在唯一的零點. 綜上所述,當a>0時,f(x)有兩個零點. 下面給出兩個練習,有興趣的可以試一下. 【練習1】設函數f(x)=(1-x)2ex. (1)討論f(x)的單調性; (2)當x≥0時,f(x)≤ax+1,求a的取值范圍. 此題在第(2)問尋找矛盾區間時需要用到賦值技巧. 答案:(1)略;(2)[1,+∞) 【練習2】已知函數f(x)=(x-1)2ex,且f(x)在x=x0處取得最小值,函數g(x)=1+kx-lnx. 已知函數F(x)=min{f(x),g(x)},若在(0,+∞)上F(x)恰有三個零點,求實數k的取值范圍. 答案:(0,e-2) 已知函數f(x)=(x+1)lnx-a(x-1).若當x∈(1,+∞)時,f(x)>0,求a的取值范圍.(端點效應) 方法二:f(x)=(x+1)lnx-a(x-1)<(x+1)(x-1)-a(x-1)=(x-1)(x+1-a),取x1=a-1,則f(x1)<0,不符合題意. 綜上,a的取值范圍是(-∞,2]. 導數壓軸題中常出現證明函數零點個數或已知零點個數求參數取值范圍的問題.解答這類題的思路主要是結合函數的單調性,應用函數零點定理找出使函數出現正、負的函數值.其中找出符合零點定理成立的恰當數值是順利攻克壓軸題的難點.導數壓軸題中的零點問題將繼續是數學高考中的熱點問題,“賦值”是關鍵,決定了數學尖子生水平的高低,教師和學生均需要多研究該類型的高考題和各省、市聯考試題.函數尋找零點的賦值問題是高考中常見的問題,而尋找點的過程是學生學習的一個難點,本文只是對這類賦值問題的方法做了一個簡單的介紹,希望有興趣的讀者繼續研究并且提供更好的方法.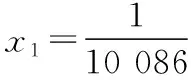
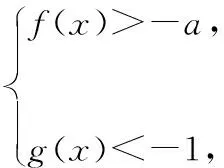
二、高考真題剖析

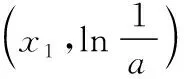
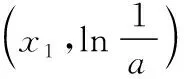

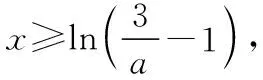

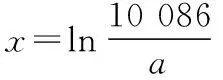
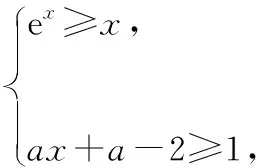



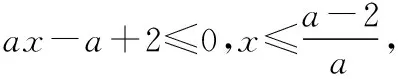
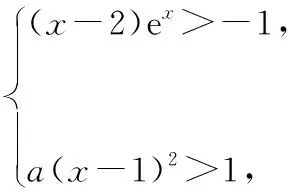

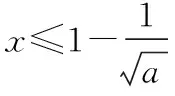

三、運用嘗試及補充
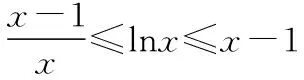
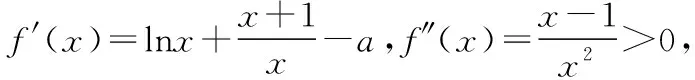
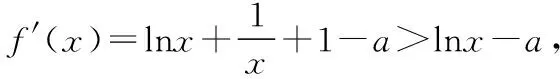
四、結束語

