模擬儲糧堆積情況探究盒維數影響因素

陳曉宇，陸 欣

（南京理工大學 能源與動力工程學院，江蘇 南京 210000）

我國是人口大國，糧食安全是國家安全的重要一項，儲糧安全便顯得尤為重要，而我國國家級儲糧方式以大型房式倉儲糧方式為主。此種方式無論是長期存放還是定期通風，作為研究對象的多孔介質糧堆的滲流特性都將是研究的重點，其中糧堆的滲透率與糧堆的溫度水分分布和通風效果密切相關，研究表明多孔介質的孔隙率是滲透率的單值函數，孔隙率可以用來確定非固結顆粒滲透率[1]。糧堆形成的結構為多孔介質形式，此種空隙結構較復雜，研究發現實際多孔介質在一定尺度范圍內具有分形的特征，且在自然儲糧過程中由于環境溫度等因素的變化產生的溫度梯度導致的微氣流流動較為緩慢，且通風過程中糧堆內氣流為層流狀態[2-3]，使得分形理論用于此研究成為一種可能。

研究發現[4]，多孔介質的分形維數越大，滲透率越大，研究多孔介質的分形維數對于多孔介質來說很重要。隨著科技的進步[5]，使用軟件模擬來保障糧食安全越來越受到人們的關注，桂便等[6]曾探索卷積神經網絡用于識別糧堆中害蟲，減少糧食的蟲害問題。本研究將從糧堆滲透率影響因素入手，使用盒維數法來探究糧堆入庫速度和堆積方式對于糧堆分形維數和滲透率的影響，為糧食合理入庫、保護糧食安全提供幫助。

1 分形多孔介質分形維數與孔隙率和滲透率的相互關系

1.1 分形維數對孔隙率的影響

分形多孔介質孔隙分形維數D是定量表征多孔介質內部不規則微觀結構特性的參數，數學表達式為：

式中D為孔隙分形維數，rmax為最大孔隙半徑，m，A0為截面面積，m2，ε為孔隙率。

由數學表達式可知多孔介質孔隙率隨孔隙分形維數的增加而呈遞增的趨勢。

1.2 分形維數對滲透率的影響

由李瑞川[4]的研究可知分形維數與滲透率的數學表達式為：

式中K為滲透率，ω為迂曲度。

迂曲度ω一般可用以下數學關系式表示：

式中a＞0為經驗常數，取0.74。

由數學表達式可知多孔介質滲透率隨孔隙分形維數的增加而呈遞增的趨勢。

由此可知研究糧堆的孔隙分形維數對于糧堆的存放和后續的通風經濟性考慮都有重要作用，糧堆的滲透率較大時，有利于糧堆溫度的控制和機械通風時能耗的減小。因而研究影響糧堆的分形維數大小的因素也就尤為重要，本文將就此展開研究與討論。

2 盒維數法介紹

為了定量地描述客觀事物的“非規則”程度，德國數學家豪斯多夫在1918年引入了維數的概念。不同方法測出來的維數名稱也不同，其中盒維數法是最常用的測分形維數方法之一，方便數學計算和經驗估計[7]。

2.1 盒維數的定義

假設分形物體為G，D是計盒維數，N(δ)是邊長δ的盒子可以覆蓋G的數目，物體的計盒維數D數學表達式如下：

實際計算時，為求出由上式定義的盒維數，可由如下方式得到：

（1）用邊長為δ的小正方形覆蓋物體G，N(δ)為覆蓋個數；

（2）取不同的邊長δ值，將會得到不同的覆蓋數目N(δ)，記錄所有數據；

（3）分別對δ和N(δ)取對數，得到ln(δ)和lnN(δ)，在對數坐標系上繪制統計曲線；

（4）選取近似直線的有效點，計算曲線斜率，斜率的負數即為所要求的計盒維數D。

盒維數的計算較為簡單，可通過計算機編程得到，因此此方法的應用十分廣泛，如紡織圖案、巖石結構、土壤和自然堆積谷物等分形的分維計算。圖2.1為一紡織圖案盒維數測量[8]。

2.2 二值法盒維數的計算

二值法[9-11]是以黑白位圖為研究對象，其計算基本思想簡單，在計算盒維數中應用廣泛。首先，對圖形文件作預處理，得到黑白位圖，并轉化為像素矩陣，在像素矩陣中黑色點用1表示，白色點用0表示；然后將像素矩陣逐次n等分，得到含有元素1的單元格，并計算單元格中非零矩陣的個數；接著，在雙對數坐標系下對計盒尺寸和對應尺寸下非零矩陣的個數進行線性回歸分析擬合，如果線性相關，得到的直線的斜率即為所求的計盒維數。二值法流程圖如下圖2.2。

圖1 一紡織圖案盒維數測量Fig.1 Dimension measurement of a textile pattern box

圖2 二值法流程圖Fig.2 Flow chart of binary method

3 驗證盒維數計算程序的準確性

為了驗證盒維數計算程序的準確性，本文首先對點圖、線性圖、平面圖、Koch雪花和Sierpinski墊片結構進行了盒維數計算驗證。驗證結果如表3.1，由結果可知誤差較小，本文計算程序是合理有效的。

表1 多種分形圖像盒維數計算結果Table 1 Calculation results of box dimension of various fractal images

4 EDEM模擬堆糧

本研究以稻谷為研究對象。

4.1 稻谷顆粒填充

稻谷的實際尺寸近似橢球，本研究以長軸為9 mm，短軸為2 mm的橢球為稻谷顆粒模型，并以此為基礎在EDEM中進行填充，填充而成的稻谷如圖3。

圖3 稻谷顆粒填充Fig.3 Rice grain filling

4.2 稻谷模擬入庫速度確定

稻谷的密度為1 020～1 210 kg/m3，本文選取密度為1 040 kg/m3，計算得到稻谷顆粒每個質量1.66×10-5kg，大型房式倉實際堆糧過程糧食入庫速度為50～200 t/h，為多個運糧機共同工作。單個運糧機皮帶輸送速度為1～40 t/h，即糧食入庫速度為1.6×104～6.69×105個/s。

本文研究對象為長29.5 m，寬17.5 m，裝糧線高5 m的房式倉。模擬糧倉為縮放模型，糧倉模型底部長59 mm，寬35 mm，顆粒工廠位于模型上方，長50 mm，寬30 mm。實際堆糧過程稻谷經過運糧機入庫形成的糧柱截面約為長0.6 m，寬0.2 m的長方形。糧食工廠生成稻谷顆粒速度為：

改變顆粒工廠生成糧食顆粒數的速度，本文選取五組數據分別為5 000、4 000、3 000、2 000、1 000 個/s。以速度5 000 個/s時為例，模擬稻谷堆積情況如圖4。

圖4 5 000個/s時稻谷堆積情況Fig.4 Rice accumulation at 5 000/s

4.3 稻谷堆積方式確定

由于糧食顆粒較為均勻，大小多為圖3所示的稻谷顆粒大小，但在稻谷生長和收割運輸過程中，自然生長或人為原因會產生少量的小顆粒稻谷。為了簡化模型，小顆粒稻谷也使用橢球模型，長軸和短軸取圖3大顆粒的一半，長軸為4.5 mm，短軸為1 mm。稻谷總數取2 500 個，大小顆粒各取1 250 個，小顆粒體積較小實際占有體積與大顆粒相比較小，符合實際情況。顆粒工廠生成速度取5 000 個/s。

為了研究將稻谷顆粒分揀開后分層堆積是否能夠增加糧堆分形維數和滲透率，將分三種堆積情況進行模擬研究，分別為大小顆粒混合堆積即糧堆自然堆積、大小顆粒分層堆積和大小顆粒分成四層堆積，以稻谷大小顆粒分成四層為例，如圖5為堆積情況（大顆粒為黑色，小顆粒為灰色）。

圖5 稻谷糧堆大小顆粒四層堆積情況Fig.5 Four layer accumulation of large and small particles in rice grain pile

5 糧食的入庫速度對分形維數的影響

對于糧食的入庫速度對分形維數的影響研究，同時要考慮到糧食入庫的效率問題，以期找到合理的糧食入庫速度，指導實際糧食的入庫。五組數據分別為5 000、4 000、3 000、2 000、1 000個/s，由于糧堆分布較為均勻，沿寬度方向孔隙率和滲透率差別不大，本文選取稻谷堆寬度方向中間位置截面圖來研究，截面圖和相應計算的分形維數和孔隙率如下圖。

圖6 5 000個/s時的分形維數和孔隙率Fig.6 Fractal dimension and porosity at 5 000/s

圖7 4 000個/s時的分形維數和孔隙率Fig.7 Fractal dimension and porosity at 4 000/s

圖8 3 000個/s時的分形維數和孔隙率Fig.8 Fractal dimension and porosity at 3 000/s

圖9 2 000個/s時的分形維數和孔隙率Fig.9 Fractal dimension and porosity at 2 000/s

圖10 1 000個/s時的分形維數和孔隙率Fig.10 Fractal dimension and porosity at 1 000/s

此時得到不同入庫速度時的分形維數和孔隙率如表2，以便求得對應滲透率。

表2 不同入庫速度分形維數和孔隙率Table 2 Fractal dimension and porosity of different warehousing speeds

將表2中的數據帶入公式1～3，得到稻谷以不同速度入庫時的滲透率，如圖11。

圖11 各速度下滲透率的值Fig.11 Permeability values at various speeds

由圖11可以看出，糧堆的滲透率隨入庫速度的增加有一種下降的趨勢，同時速度較低時滲透率差別不大，而速度過慢又會對堆糧工作的效率產生影響，權衡兩種因素，得到3 000 個/s是本次模擬中較為合適的入庫速度。

由公式5逆推導得到本次模擬較為合理的單個運糧機運糧速度為14.3 t/h，整倉入庫速度根據倉房大小選取合適的運糧機個數即可計算求得。

6 糧食的堆積方式對分形維數的影響

由于此次模擬儲糧的堆積方式為豎直方向不同的分層分布，沿寬度方向孔隙率和滲透率差別不大，仍然選取稻谷堆寬度方向中間位置截面圖來研究。三種情況分別為大小顆粒混合堆積即糧堆自然堆積、大小顆粒分層堆積和大小顆粒分成四層堆積，如下圖所示（大顆粒為黑色，小顆粒為灰色），為不同堆積方式的分形維數和孔隙率：

將圖12～14中的數據帶入公式1～3，得到稻谷以不同堆積方式入庫時的滲透率，如圖15：

圖12 大小顆粒混合時的分形維數和孔隙率Fig.12 Fractal dimension and porosity of mixed particles

圖13 大小顆粒分層時的分形維數和孔隙率Fig.13 Fractal dimension and porosity of stratified particles

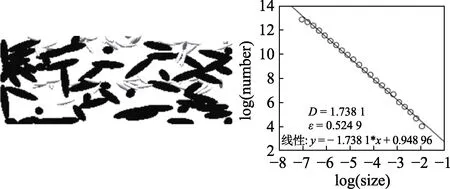
圖14 大小顆粒分成四層時的分形維數和孔隙率Fig.14 F ractal dimension and porosity of large and small particles divided into four layers

圖15 各堆積方式下滲透率的值Fig.15 Permeability value under each accumulation mode

由圖可以看出，由于糧食顆粒較為均勻，模擬的小顆粒較少，三種堆積方式下滲透率差別比較小，同時看出分層越多越接近于混合方式，與實際情況相符。可以看出自然混合方式堆積時糧堆滲透率最大，即自然堆積方式是糧食堆積比較有利的方式。

7 結論

通過以上的模擬與分析，可以得出以下結論：

（1）糧倉堆積的糧堆具有分形特性，可以使用分形理論對多孔糧堆進行研究與分析；

（2）糧堆分形維數與滲透率正相關，較大的糧堆滲透率有利于后續糧堆的溫度控制和機械通風降溫能耗的降低，即較大的分形維數有利于儲糧安全；

（3）堆糧的入庫速度對于糧堆的滲透率有較大影響，單個運糧機速度為14.3 t/h時，分形維數較大，滲透率較大，同時不影響堆糧的效率，這對于現實堆糧過程具有參考意義；

（4）糧堆的堆積方式由于糧食本身具有均勻性的特點，所以采用較少的小顆粒進行模擬，發現堆積方式對于滲透率的影響比較少，自由堆積的方式即是對于糧食比較有利的堆積方式。