盾構綜合管廊人員疏散可靠度計算

譚宜瑋，劉叔灼，陳俊生

(1.華南理工大學 土木與交通學院，廣東 廣州 510641；2.華南理工大學 土木與交通學院 亞熱帶建筑科學國家重點實驗室，廣東 廣州 510640)

隨著綜合管廊建設在各大城市的不斷進行，不影響城市市容和擁有較好經濟效益的盾構工法管廊很好地滿足了城市施工的復雜要求[1]。但相較于已經成熟的施工設計，盾構管廊的后期運維問題卻缺乏規范性的指導[2]。

關于管廊災后人員逃生研究，翟越等[3]開展了綜合管廊火災風險和人員疏散的數值模擬研究。徐志勝等[4]運用FDS(fire dynamics simulator)和Pathfinder軟件分別得出了管廊電力艙端部和中部發生火災時的人員逃生情況。Seike等[5]進行了在煙氣環境下的隧道人員安全逃生實驗。譚妍[6]通過Monte Carlo法與數值模擬研究了軌道隧道不同風險區域人員死亡概率。王琛琛[7]運用Monte Carlo法，得到隧道最不利點列車火災情況下人員必需疏散時間樣本。奚學東等[8]根據煙氣臨界溫度建立了公路隧道人員可用安全疏散時間預測模型。郭雄[9]運用數值模擬方法以及Agent-base連續性模型對綜合管廊人員疏散進行研究。Lemaire等[10]在第二個荷比盧聯盟隧道進行了14次全規模火災試驗，得到了發生火災下的不同人員行為模式及概率分布情況。Carvel等[11]運用貝葉斯理論對隧道火災進行分析。宗燕燕[12]利用PyroSim火災軟件和Pathfinder軟件來對綜合管廊施工中的火災事故進行仿真模擬。尚琳等[13]分析了綜合管廊中不同能見度和煙氣對人員安全疏散時間的影響。呂勇[14]采用Andres Noren的隧道火災人員疏散試驗統計，對公路隧道不同火災規模下的人員逃生進行了研究。

總結前人的研究成果，發現管廊人員疏散研究大多集中于明、暗挖短距離管廊，針對盾構管廊的研究較少，且成果多為人員逃生與否，未考慮人員逃生的不確定性。本研究依托廣州市天河智慧城盾構段綜合管廊項目，在充分考慮管廊人員逃生特點的基礎上，對隧道災后人員逃生行為概率模型進行了優化，引入了疏散可靠度概念，通過對火災模型建模，數值分析軟件的隨機模擬，得出了盾構管廊的災后人員逃生可靠度，從概率角度描述了管廊人員的災后疏散結果。針對此問題，本文截取盾構管廊后期運維問題中的管廊災后人員安全疏散內容進行研究，以期為日后盾構管廊運維規范的編制提供參考。

1 研究方法

1.1 疏散可靠度

在結構工程中，可靠度又稱為可靠性，指的是結構在規定的時間、規定的條件下完成預定功能的能力[15]，當以概率來度量時稱為可靠度。當研究內容由結構的安全承載轉移到盾構管廊內的人員安全疏散研究中時，可靠度指的是在廊內發生火災時檢修人員能夠安全逃生的概率。

人員安全逃生的概率由管廊發生火災時的可用安全疏散時間Taset和人員逃生的必須安全疏散時間Trset決定，人員安全疏散概率為P=P(Taset-Trset>0)[16]，此處人員安全疏散概率即為人員安全疏散可靠度。

Monte Carlo法是常用的計算可靠度的方法，該方法基于大數定律，通過計算機輔助生成隨機數，并利用隨機數來模擬真實的隨機結果。由功能函數生成功能函數值即必須安全疏散時間Trset，與可用安全疏散時間Taset比較，超過可用安全疏散時間即視為逃生失敗，失敗次數與總模擬次數的比值近似為逃生失敗概率，當模擬次數趨近于無窮大時，逃生概率即趨近于真實結果。

功能函數Z=g(X1，X2，…，Xn)，X1、X2、…、Xn為相互獨立的隨機變量，已知Xi所服從的概率分布，將每個變量都進行N次相同的服從其分布的隨機抽樣，得到由Ri列向量(Xi1，Xi2，…，Xin)T所組成的矩陣數表Z：

將矩陣中的每一列元素分別代入功能函數，得出逃生失敗的總次數Nf，則逃生失敗概率可表示為：

1.2 研究步驟

本次研究使用PyroSim軟件進行盾構管廊火災建模，得出盾構管廊火災特性的相關參數，以在一側防火門附近發生火災為最不利工況，使用防火門或者中隔板處CO濃度限度為指標(CO是所有火災煙氣中最主要的致死性氣體, 也是唯一被證實造成火災中人員大量死亡的氣體[17])，從火災發生到CO濃度達到人體安全限度的時間為可用安全疏散時間Taset。

人員必須安全疏散時間借由荷蘭Benelux隧道實驗結果建立疏散模型[10]。在一個防火區間內，通過Matlab編寫程序模擬得出人員疏散時間隨機數，再由Monte Carlo法建立功能方程，通過Matlab得出的隨機變數，以火災數值模擬軟件得到的可用安全疏散時間Taset為一定值，進行每次隨機模擬的人員安全類別判斷，進而得出盾構管廊內發生火災時的人員安全疏散可靠度，即疏散概率。

人員的必須安全疏散時間由察覺火災跡象時間tfeel、確認火災時間tsure和人員逃離時間tmove三部分組成，即Trset=tfeel+tsure+tmove。但考慮到實際情況中，進入盾構管廊內的都為專業的檢修人員，且定期的安全疏散演練也為檢修人員在發生火災時做出正確的決策做出了保障，對火災發生的敏感性較為統一，并且做到即察即走。基于上述情況，對概率模型進行優化。研究步驟流程圖見圖1。

圖1 研究步驟流程圖Fig.1 Flow chart of the research procedure

1.3 依托項目

本研究依托于廣州市天河智慧城地下綜合管廊工程。天河智慧城地下綜合管廊總長約19 390 m，因科韻路、科翔路至華觀路無明挖施工條件，采用非開挖盾構法施工，盾構段長8 620 m，為圓形斷面，外徑6 m，內徑5.4 m，豎井間距為600～1 000 m，分為上下兩艙，上半部分為電力艙，入廊管線為阻燃的高壓電力電纜(220 kV、110 kV)，下半部分為綜合艙，內設有供水主管(DN1000)、通信干線。管廊斷面如圖2所示。

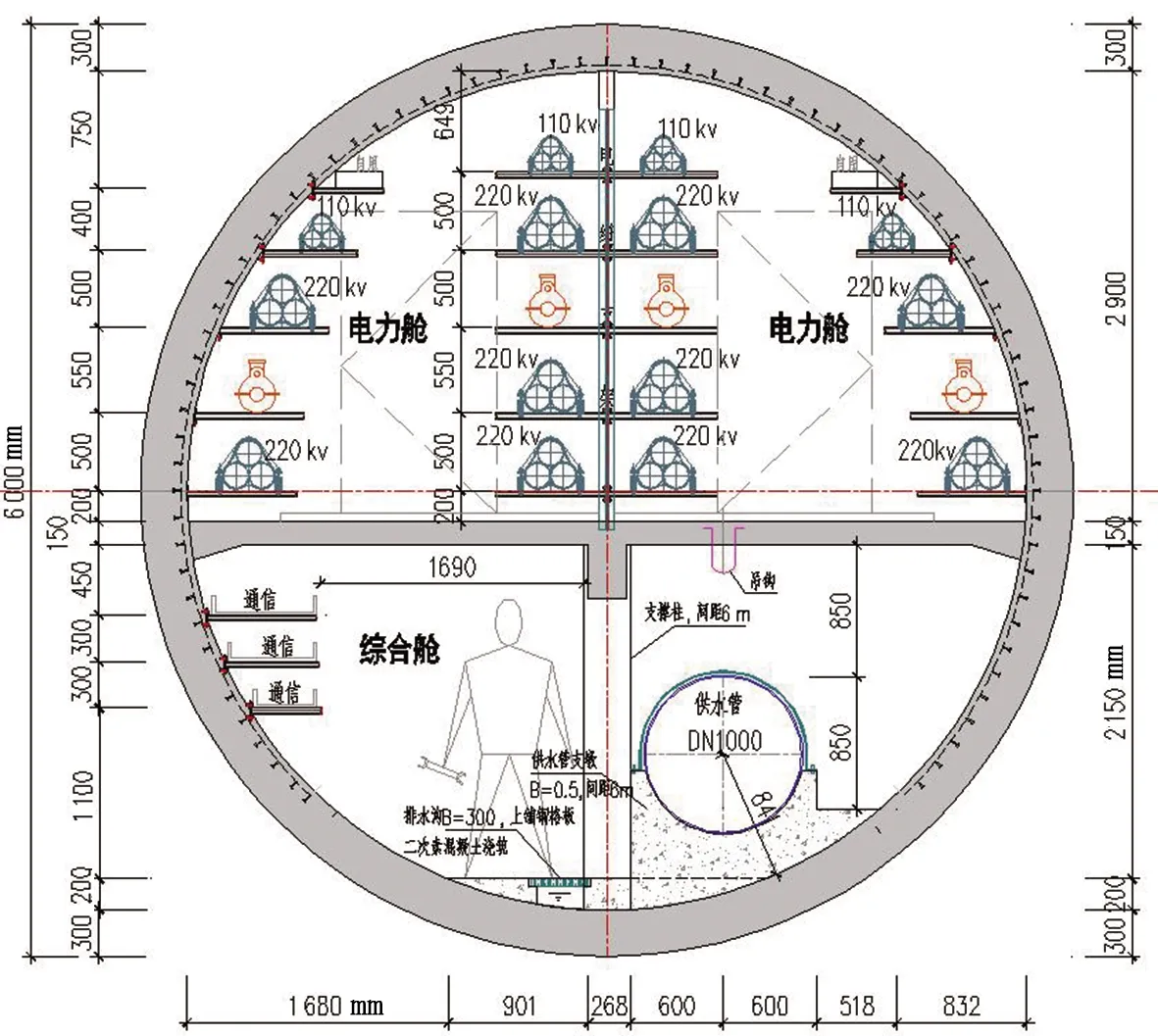
圖2 盾構管廊典型斷面圖Fig.2 Typical section view of a shield tunnel

2 火災模型的建立以及可用安全疏散時間的計算

2.1 火災模型

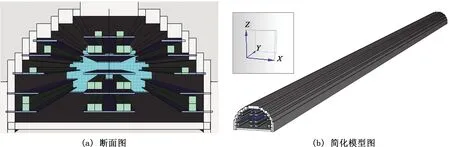
圖3 盾構管廊模型Fig.3 Model diagram of the shield tunnel

2.1.1 模擬參數設置

模擬采用網格尺寸為0.4 m×0.4 m×0.2 m的四邊形網格結構，網格總數為135 000。以對人員疏散最不利的火源位置為設計工況，即火源位于Y=200(即防火門附近)中間底層電纜下方，考慮到電纜材料(導體為銅芯，絕緣材料為聚乙烯，護套材料為聚氯乙烯)發生火災的規模以及參考文獻[17]，火源功率總量設置為2 300 kW，面積為0.4 m×0.4 m。與火源有關的相關參數：環境空氣密度為1.205 kg/m3，環境空氣比熱容為1.005 kJ/(kg·K)，環境濕度為273 K，重力加速度取9.81 m/s2。模擬時間為火災發生后的10 min內，即持續時間為600 s。電纜采用聚氯乙烯電纜，熱釋放速率為265 kw/m2，密度為1 380 kg/m3，比熱容為1.289 kJ/(kg·K)，電導率為0.192 W/(m·K)。

2.1.2 測點設置

如圖4所示，在人眼特征高度1.6 m處，沿管廊縱向每隔25 m設置CO濃度測量設備，得到管廊的CO濃度縱向分布規律。

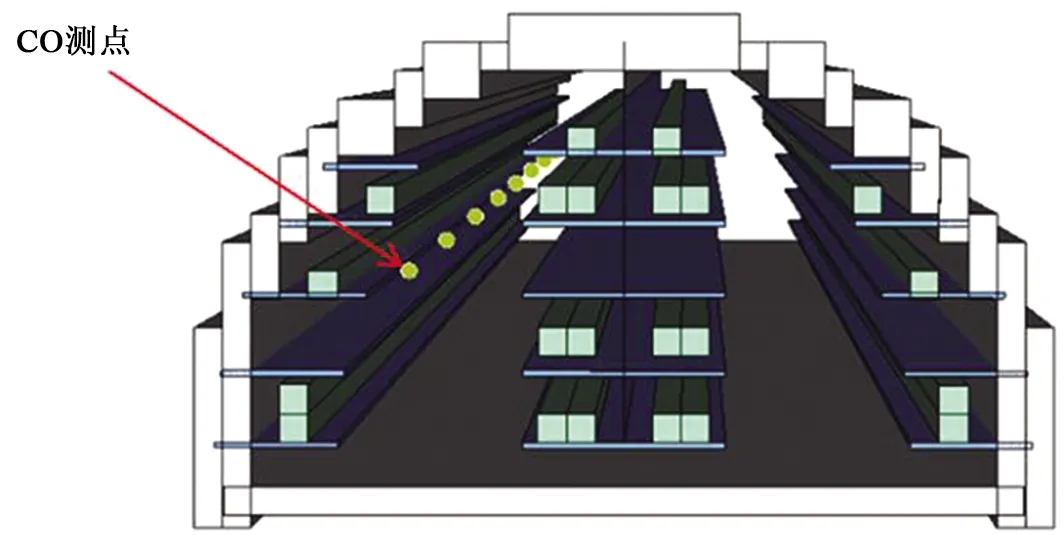
圖4 CO濃度測點布置圖Fig.4 Layout of CO concentration measuring location

2.2 可用安全疏散時間的計算

2.2.1 計算方法

通過PyroSim軟件模擬出最不利的情況即火災發生在一側防火門附近，管廊內CO體積分數分布。

從火災發生開始到防火門或者中隔板處CO分布開始超過人體在環境中承受的安全范圍(空氣中CO體積分數超過0.08%時，將會使人產生眼花、痙攣的癥狀，并且在2～3 h死亡，本文以CO體積分數0.1%作為人體的安全濃度界限[9])的這段時間，即為可用安全疏散時間Taset。

2.2.2 可用安全疏散時間

根據模擬結果，火災開始大約404 s后，防火門附近或者中隔板附近的CO體積分數達到0.1%，即可用疏散時間Taset約為404 s。防火門CO體積分數變化情況如圖5所示。

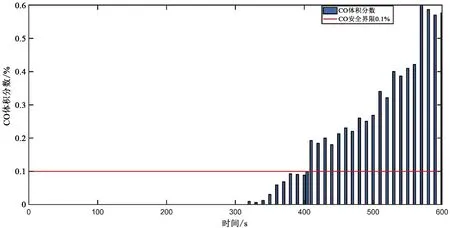
圖5 布置在背離火源的防火門附近的測點CO體積分數隨時間變化圖Fig.5 Graph of CO concentration variation over time at the measuring location located near the fire door that is away from the fire source

3疏散模型的建立及必須安全疏散時間的抽樣模擬

3.1 疏散模型

3.1.1 火災下人員疏散行為概率模型

荷蘭Benelux隧道實驗中將火災環境下人員的不同疏散行為進行了概率統計分析，劃分了以下六組不同的疏散概率行為[6，10]。詳見表1～2。

表1 疏散行為分組表Table 1 Evacuation behavior grouping

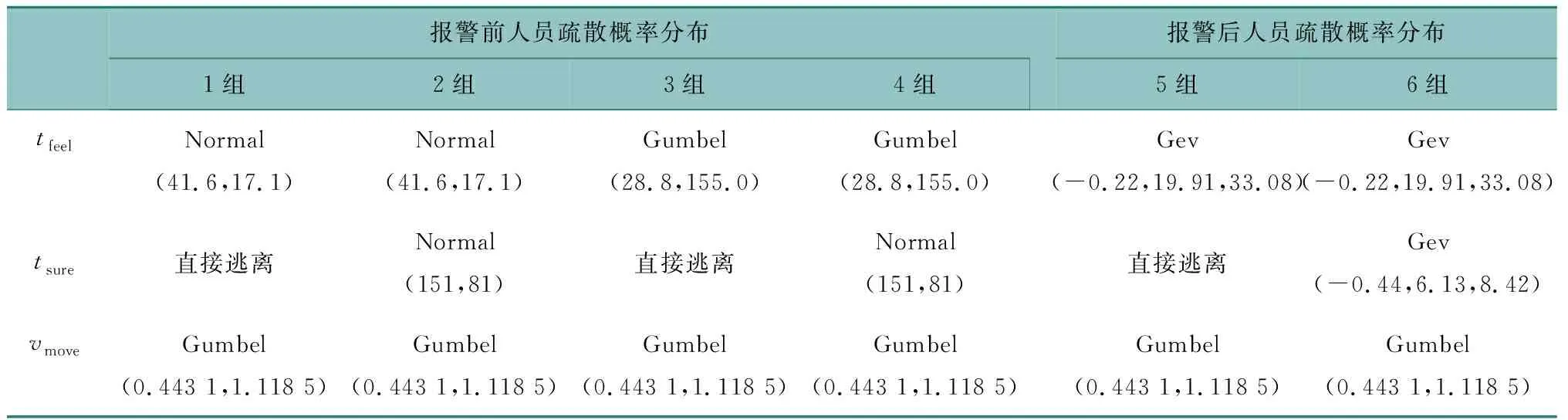
表2 疏散行為概率分布表Table 2 Evacuation behavior probability distribution

3.1.2 模擬工況設置

人員的必須安全疏散時間由察覺火災跡象時間tfeel、確認火災時間tsure和人員逃離時間tmove三部分組成，即Trset=tfeel+tsure+tmove。模擬分設兩工況，均在200 m的一個防火區間內進行：工況1為正常情況下普通人員疏散逃生模擬；考慮到能夠進入管廊艙內的都為檢修人員，且平時無其他閑雜人員進入，在日常的安全教育及疏散演練下，檢修人員感知火災發生的敏感性較為統一，日常的訓練也能使檢修人員在面臨危險時及時疏散逃生，故將察覺火災跡象時間tfeel簡化為常量，且忽略確認火災時間tsure，基于此，對概率模型進行優化，分設工況2、3、4，如表3、4所示，工況2、3、4也更符合受到合格火災逃生培訓的檢修人員在火災疏散中的表現。

表3 疏散模擬工況設置表Table 3 Evacuation simulation condition setting

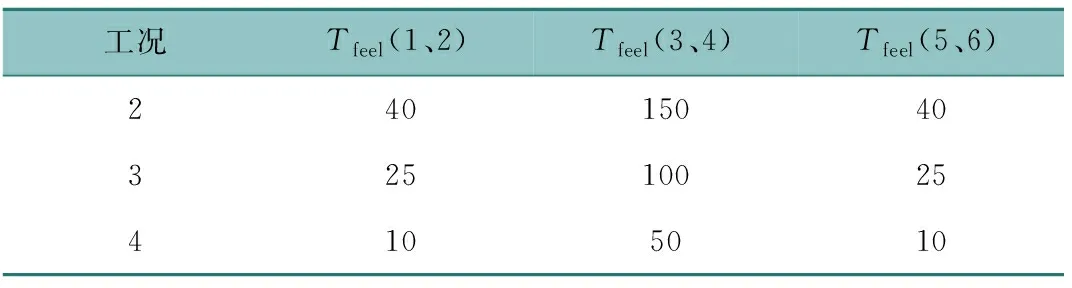
表4 工況2、3、4察覺時間設置表Table 4 Detection time setting for working conditions 2, 3 and 4 單位：s

3.2 不同疏散時間的概率分布

3.2.1 察覺火災時間

管廊內人員察覺火災有兩種群體行為：(1)在火災報警前即察覺，察覺火災時間服從Normal分布或Gumbel分布；(2)在火災報警后察覺，察覺火災時間服從Gev分布。

察覺火災時間Tfeel各分組行為的概率分布為：tfeel(1、2)=Normal(41.6，17.1)，tfeel(3、4)=Gumbel(28.8，155)，tfeel(5、6)=Gev(-0.22，19.91，33.08)。

3.2.2 確認火災時間

管廊內人員確認火災同樣有兩種群體行為：(1)在火災報警前即察覺，直接逃離或確認火災時間服從Normal分布；(2)在火災報警后察覺，直接逃離或確認火災時間服從Gev分布。

確認火災時間Tsure各分組行為的概率分布為：tsure(2、4)=Normal(151，81)，tsure(6)=Gev(-0.44，6.13，8.42)。

3.2.3 人員逃離時間

管廊內人員距離防火門的長度L與人員的逃離速度V之比即為人員逃離時間，計算如下式所示：

tmove=L/V

(1)

式中L、V均為由Matlab生成的服從各自概率分布的隨機數，V為逃生速度，其概率分布為V=Gumb(0.443 1，1.118 5)，L為人員距離防火門位置，上文中一個防火分區長度為200 m，其概率分布為L=rand(0，200)。

3.3 疏散時間模擬樣本及可靠度計算

3.3.1 不同疏散時間模擬樣本

通過 Matlab 編程計算進行隨機抽樣模擬，每組行為隨機模擬人數設為1 000，每組行為的疏散模擬總時間為察覺時間tfeel、確認時間tsure和逃離時間tmove之和，程序模擬得出不同概率行為不同分布的隨機抽樣樣本，如圖6所示。

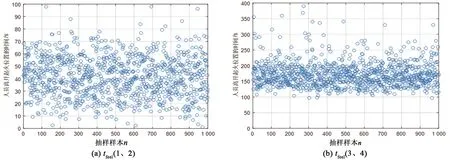
圖6 不同疏散時間模擬樣本圖Fig.6 Simulation sample diagram of different evacuation times

圖6(續)

3.3.2 工況1人員疏散總時間及可靠度計算

人員必須安全疏散時間Trset=tfeel+tsure+tmove，按照不同分組的人群疏散行為，將各不同時間進行組合，得到工況1的人員疏散總時間，如圖7所示，工況1必須安全疏散時間與可用安全疏散時間Taset=404 s的對比如圖8所示。

圖7 工況1人員疏散總時間樣本圖 Fig.7 Sample diagram of total evacuation time of working condition 1

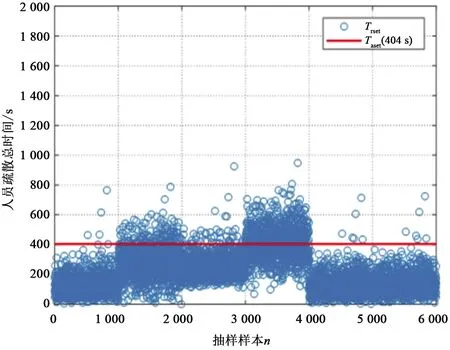
圖8 工況1時間對比圖 Fig.8 Time comparison diagram of working condition 1

由人員逃生的概率計算公式P=P(Taset-Trset>0)，進行多次模擬得出工況1普通人員的疏散可靠度約為0.889 4，人員疏散失敗的概率約為11.06%。

3.3.3 工況2、3、4人員疏散總時間及可靠度計算

工況2、3、4的人員疏散總時間分別如圖9所示，工況2、3、4必須安全疏散時間與可用安全疏散時間Taset=404 s的對比分別如圖10所示。

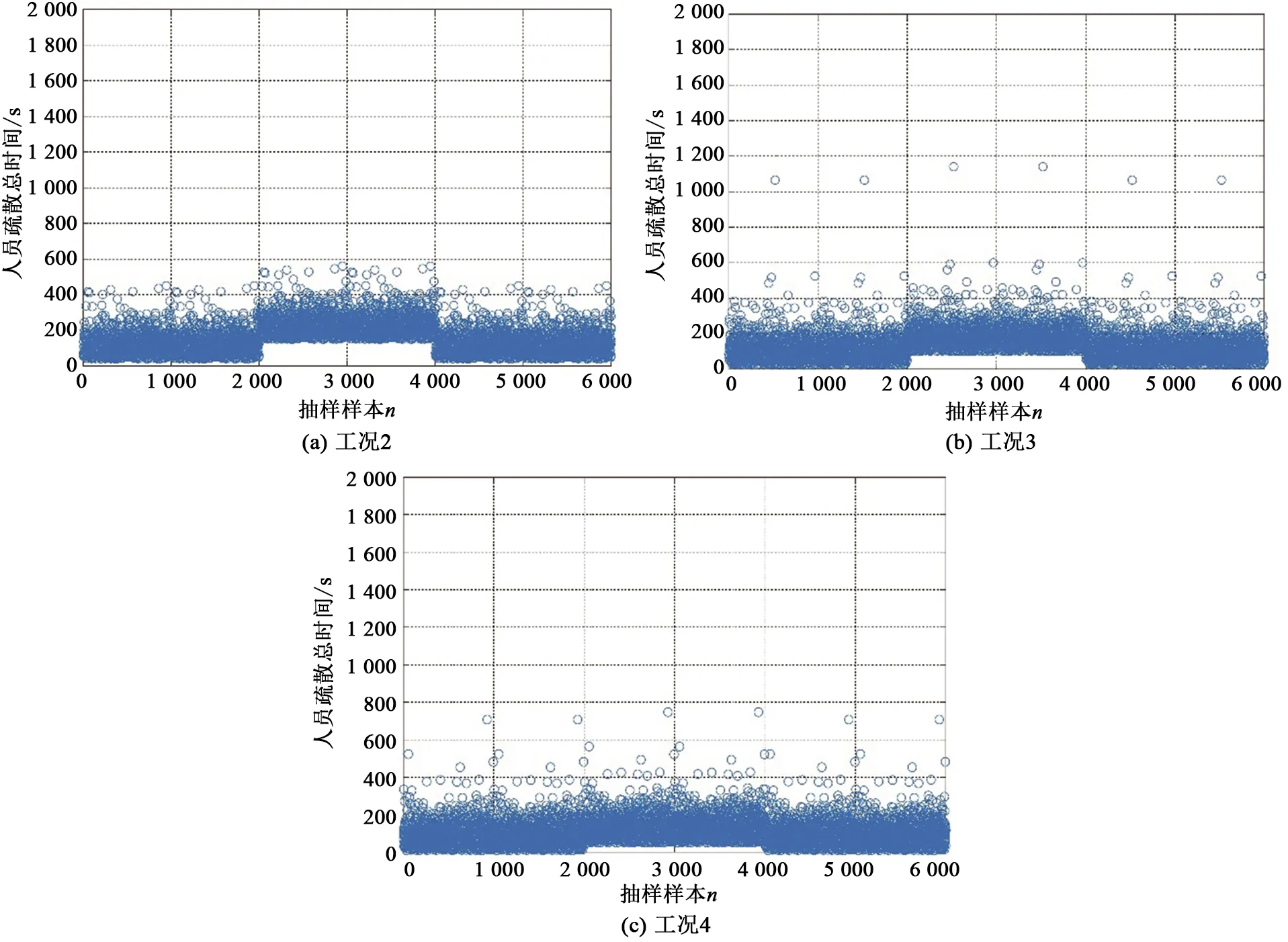
圖9 工況2、3、4人員疏散總時間樣本圖Fig.9 Sample diagram of total evacuation time of working conditions 2,3 and 4

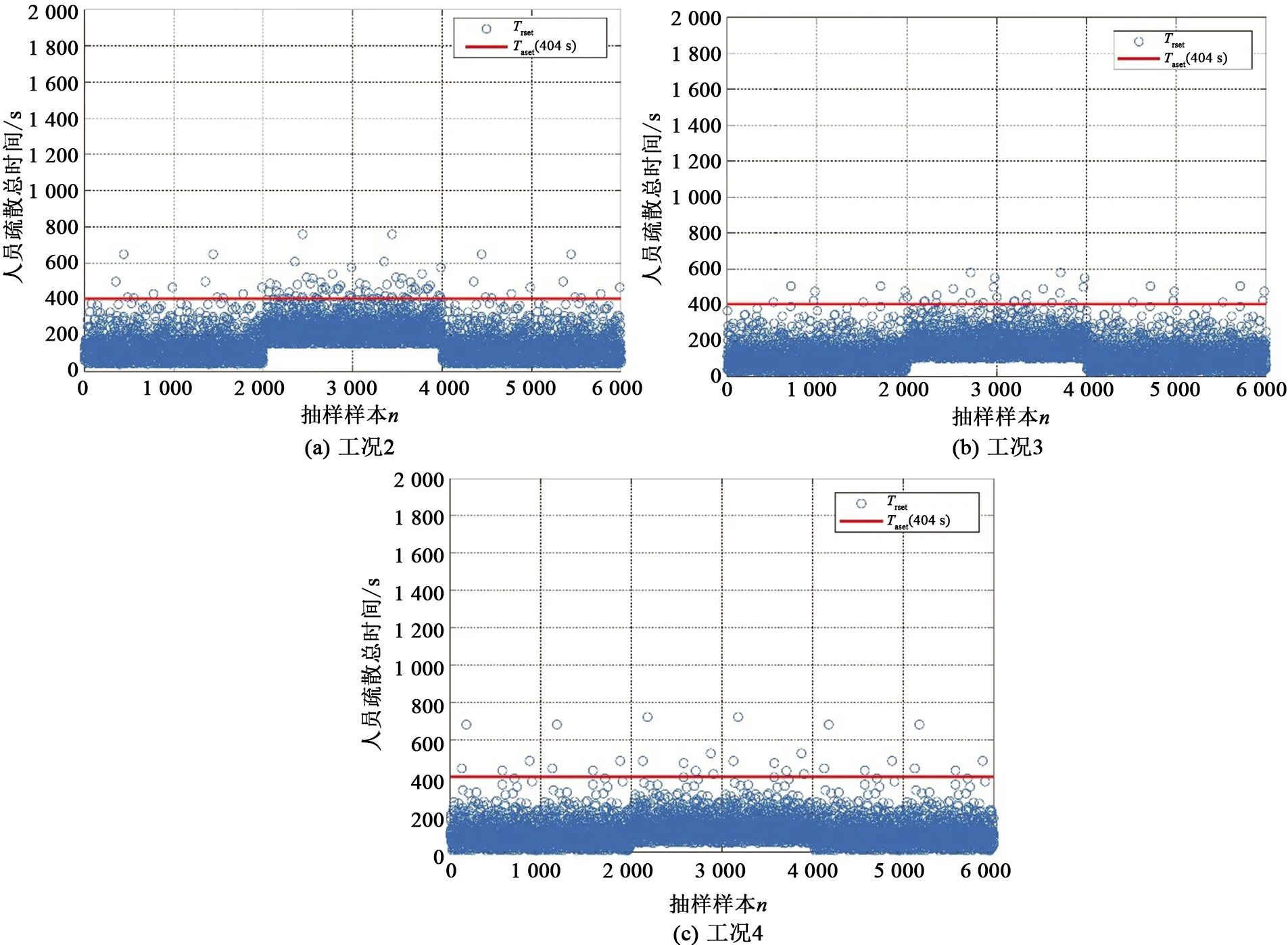
圖10 工況2、3、4時間對比圖Fig.10 Time comparison diagram of working conditions 2,3 and 4

由人員逃生的概率計算公式P=P(Taset-Trset>0)，進行多次模擬得出工況2、3、4檢修人員的疏散可靠度分別約為0.988 3、0.994 2、0.995 3，疏散失敗概率分別約為1.17%、0.58%、0.47%，詳見表5。

表5 各工況疏散可靠度對比表Table 5 Comparison of evacuation reliability under various working conditions

通過Monte Carlo法得到大量樣本的必須安全疏散時間，并考慮到檢修人員的實際情況，與PyroSim軟件模擬得到的可用安全疏散時間進行比較，并進行數理統計得到結論：當火災發生時，在一個200 m防火區間內，普通人員的疏散可靠度約為0.889，檢修人員的疏散可靠度約為0.99，趨近于1，且由工況1與工況2、3、4對比，日常的疏散演習和安全規范手冊等控制手段能顯著提高疏散可靠度。

4 結語

使用PyroSim火災模擬軟件和Matlab數值分析軟件，將優化的隧道人員疏散概率模型應用于管廊人員疏散研究中，從概率角度通過Monte Carlo方法計算出了疏散可靠度，得出主要結論如下：(1)通過工況1和優化過概率模型的工況2、3、4，得出在一個防火區間內普通人員的疏散可靠度約為0.889，檢修人員的疏散可靠度約為0.99，趨近于1；(2)工況1與工況2、3、4對比，說明在實際情況中，日常的疏散演習和安全規范手冊等控制手段能夠對檢修人員的安全提供極大的保障；(3)工況2、3、4說明，隨著人員安全素質的提高，遇到危險后“化險為夷”的可能性越大，在日后的管廊運維過程中，需重視這類的預防措施。研究考慮了人員疏散過程中的隨機性因素，引入了概率與隨機性分析，從更為科學的角度研究了此類問題，希望能為未來盾構管廊運維規范的編制提供幫助。