例析質點系牛頓第二定律在連接體問題中的應用

許冬保

(江西省九江第一中學 332000)

在動力學問題中，若質點系中質點的加速度不盡相同，原則上應用隔離法處理有關問題.若使用整體法，則需要根據質點系牛頓第二定律來建立方程.在一般教輔資料中均有介紹，本文不作贅述.以下例談質點系牛頓第二定律在連接體問題中的拓展應用.

1 質點系牛頓第二定律

在質點系中，若質點的加速度不同，根據力的獨立作用原理，可以導出質點系牛頓第二定律的形式

2 質點系牛頓第二定律在連接體問題中的應用

2.1 平動連接體問題(加速度大小相等、方向不同的質點系)

例1利用圖1所示實驗裝置及打點計時器(圖中未畫出)來驗證“在小車質量不變的情況下，小車的加速度與作用力成正比”的結論，并直接以鉤碼所受重力mg作為小車受到的合外力，則實驗中應采取的改進措施是什么？鉤碼的質量m與小車的質量M之間應滿足的條件是什么？

圖1

解析據題意，實驗設計方法是直接以鉤碼所受重力mg作為小車受到的合外力，需要考慮兩方面的問題：第一方面是必須消除摩擦力因素的影響，因此需要平衡(或補償)摩擦力；第二方面是小車的牽引力等于繩對小車的拉力，該拉力小于鉤碼所受重力，顯然繩子的拉力近似等于鉤碼所受重力mg需要滿足一定的條件.分析如下：

設小車質量為M，小車所受牽引力為F，由牛頓第二定律，有

F=Ma

mg-F=ma

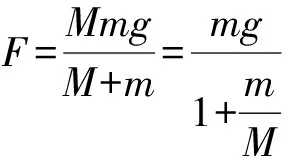
顯然，當M?m時，F≈mg.

因此，實驗時若直接以鉤碼所受重力mg作為小車受到的合外力，需要采取的改進措施是平衡(或補償)摩擦力，且使得小車的質量M遠遠大于鉤碼的質量m.

點評小車及鉤碼運動的加速度大小相等但方向不同，可否用質點系牛頓第二定律求解？我們可以將原實驗裝置進行等效變換，如圖2所示，鉤碼所受重力為動力，則有mg=(M+m)a，再隔離其中一個物體為對象列式，可得同樣的結果.

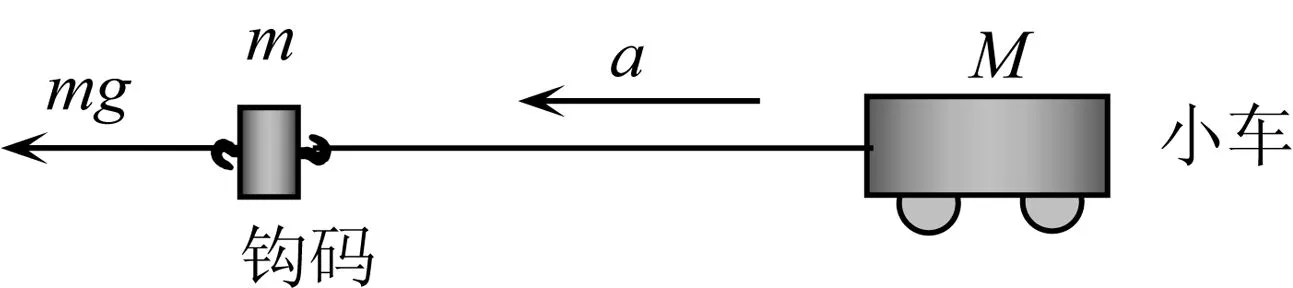
圖2

例2 如圖3所示為阿特武德機的示意圖，它是早期測量重力加速度的器械，由英國數學家和物理學家阿特武德于1784年制成.他將質量同為M的重物用繩連接后，放在光滑的輕質滑輪上，處于靜止狀態.再在一個重物上附加一質量為m的小重物，這時，由于小重物的重力而使質點系做初速度為零的緩慢加速運動并測出加速度.若不計空氣阻力，求質點系的加速度大小.

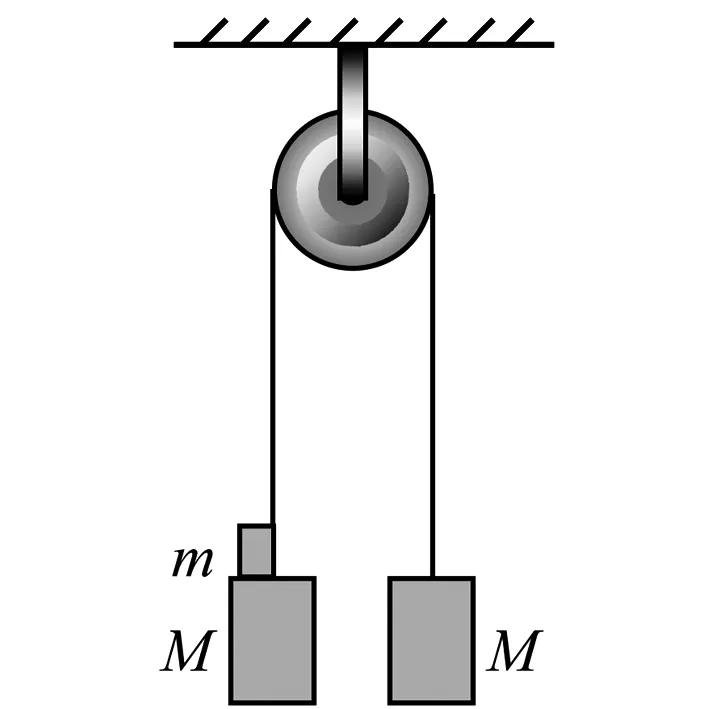
圖3

解析設繩中的張力為T，加速度為a.由牛頓第二定律，有

(m+M)g-T=(m+M)a

T-Mg=Ma

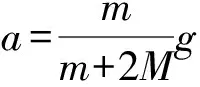
點評此類問題一般用隔離法分析列式，若用質點系牛頓第二定律求解，同樣可將質點系等效為如圖4所示的情形，顯然，(m+M)g-Mg=(m+2M)a，所得結果同上.

圖4

2.2 轉動連接體問題(加速度大小不等、方向共線的質點系)

例3 如圖5，用長為L的輕繩(輕繩不可伸長)連接的甲、乙兩物塊(均可視為質點)，放置在水平圓盤上，甲、乙連線的延長線過圓盤的圓心O，甲與圓心O的距離也為L，甲、乙兩物塊的質量均為m，與圓盤間的動摩擦因數均為μ，物塊與圓盤間的最大靜摩擦力等于滑動摩擦力，甲、乙始終相對圓盤靜止，則下列說法中正確的是( ).

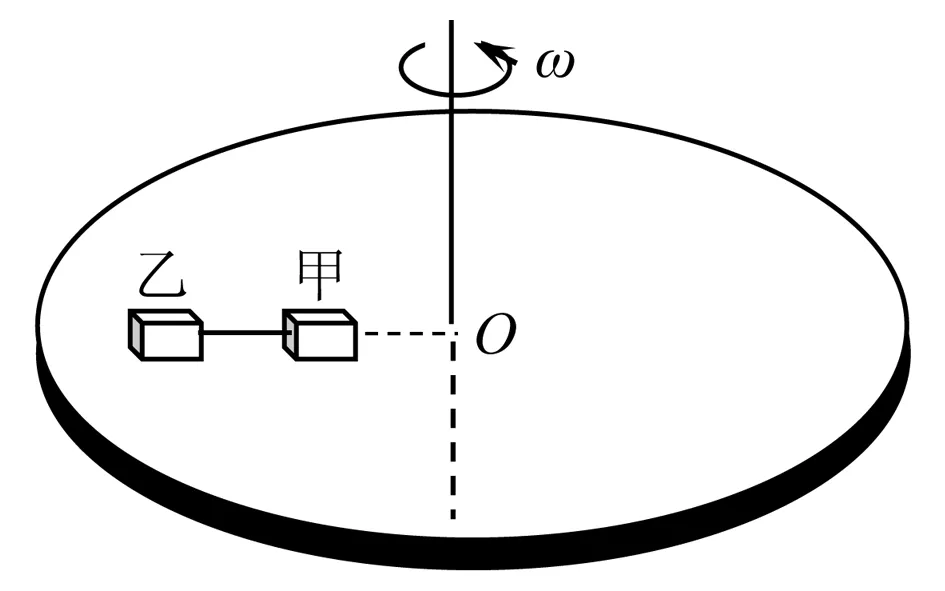
圖5

D.輕繩最大彈力為μmg

解析由題給信息知，乙做勻速圓周運動所需要的向心力是甲的兩倍，而甲、乙兩物塊受到圓盤的最大靜摩擦力相等，因此，乙最先達到最大靜摩擦力，隨圓盤轉速增大，繩中開始出現張力，直到甲亦達到最大靜摩擦力，此為臨界狀態.對應圓盤的最大角速度及繩中最大彈力.

考察甲、乙兩物塊做勻速圓周運動的向心加速度大小不等、但方向相同.設圓盤轉動的最大角速度為ω.選取指向圓心的方向為正方向，則由質點系牛頓第二定律，有

μmg+μmg=mLω2+2mLω2

設繩中最大張力為F，選擇甲(或乙)物塊為研究對象，由牛頓第二定律，有

選項B、C正確.

點評兩物塊均做勻速圓周運動，考慮到兩物塊的加速度不同，通常是選用隔離法來處理.分別對甲、乙兩物塊，由牛頓第二定律，有μmg-F=mLω2，μmg+F=2mLω2.聯立求解，結果同上.比較可知，應用質點系牛頓第二定律求角速度非常簡潔.

例4如圖6，在水平圓盤上放有質量為m、m和2m可視為質點的三個物體A、B、C，圓盤可繞中心軸OO′轉動，且角速度可調，三物與圓盤的動摩擦因數均為μ.已知A、B、C三個物體與軸O共線，且OA=OB=BC=r，現將三個物體用輕質細線相連，保持細線伸直且無張力，然后讓圓盤從靜止開始繞轉軸緩慢的加速轉動，用ω表示圓盤轉動的角速度，取重力加速度為g，最大靜摩擦力等于滑動摩擦力，下列說法正確的是( ).

圖6

A.A所需要的向心力增加最快

解析在三個物體中，C所需要的向心力最大，即C所需要的向心力增加最快，選項A錯誤；B、C間細線出現張力的條件是

2μmg<2m·2r·ω2

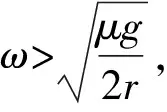
質點系剛要滑動時，物體A、B、C所受摩擦力均達最大值，此時，A所摩擦力方向一定背離圓心指向外側.選取圖6中此時指向圓心向左的方向為矢量正方向，由質點系牛頓第二定律，有

μmg+2μmg+μmg=mrω2+4mrω2-mrω2

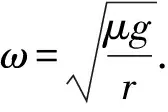
綜上，無論是平動連接體問題，還是轉動連接體問題，在應用質點系牛頓第二定律建立方程的過程中，要通過變換、等效使加速度方向共線，簡化為一維情形.