一類時空分數階非線性偏微分方程的對稱分析、對稱約化、精確解和守恒律

谷瓊雅,時振華,王麗真,何靜

(西北大學數學學院,陜西 西安 710127)

1 引言

近些年,隨著分數階微分方程在工程、物理、生物等領域的廣泛應用[1],人們越來越關注分數階微分方程的研究,其中構造分數階偏微分方程的精確解是偏微分方程理論研究中非常重要的問題[2-3].大量研究論文已引入多種構造精確解的方法,如不變子空間法[4]、q-HAM方法[4]、齊次平衡法[5]、泛函分離變量法[6]、廣義分離變量法[6]等.李對稱分析是研究偏微分方程的重要方法和途徑.微分方程的不變性質和其所描述的重要的物理現象都與其李對稱密切相關.

李對稱分析由Sophus Lie在十九世紀首次提出并用于整數階微分方程的群分析中.隨后,文獻[7]提出分數階導數和李對稱的分數階延拓公式,由此李對稱分析被推廣到分數階微分方程的研究中.許多學者利用李對稱分析研究了時間分數階偏微分方程,例如,文獻[8]對時間分數階Harry-Dym方程進行李對稱分析,并構造了方程的群不變解.文獻[9-10]分別對時間分數階Navier-Stokes方程組和Keller-Segel方程組進行李對稱分析并構造出守恒律.還有一些學者利用李群分析對方程進行群分類,文獻[11]對時間分數階擴散方程進行群分類,并做相對應的對稱約化得到方程的不變解.僅有少部分學者利用李對稱分析研究時空分數階偏微分方程,例如,文獻[12]對時空分數階Rosenou-Haynam方程進行了李對稱分析,文獻[13]對時空分數階非線性演化方程進行了對稱分析.

Noether定理建立了守恒律和對稱之間的聯系.文獻[14]提出了一個新的守恒定理,即建立沒有經典拉格朗日方程的微分方程的守恒定律.在此定理的基礎上,文獻[15]建立了時間分數階微分方程的守恒律,文獻[12]建立了時空分數階Rosenou-Haynam方程的守恒律.本文將在李對稱的基礎上建立一類時空分數階非線性方程的守恒律.

雙多孔介質方程在物理、工程科學等方面有很多應用.文獻[16]研究了整數階雙多孔介質方程的奇解和解的漸進行為.文獻[17]用不變子空間方法對整數階雙多孔介質方程進行研究求解.文獻[18]研究了具有非發散算子的雙多孔介質方程的爆破和關鍵指數分析.文獻[19]通過構造修正多孔介質方程的自相似解,研究了修正多孔介質方程的一族自相似解的存在性.文獻[20]用李對稱分析研究了時空分數階多孔介質類型方程并利用李代數得到方程的群不變解.本文將利用李對稱分析對一類形式簡單的廣義時空分數階雙多孔介質方程進行研究.廣義的時空分數階雙多孔介質方程為

其中,(i=1,2,3)分別為關于t和x的分數階Riemann-Liouville導數.u是關于x,t的未知函數,0＜α＜1,1＜βi＜2(i=1,2,3),0,b,c均為實數.

本文考慮方程(1)中b=c=0的情形,在這種情況下,方程(1)變為如下的時空分數階非線性偏微分方程

特別地,當β=2時,方程(2)變為如下的時間分數階非線性偏微分方程

本文將構造方程(2)和方程(3)所允許的李代數、一維優化系統和精確解,并對方程(2)的守恒律進行研究.本文結構如下:在第二節,介紹本篇文章所涉及的基礎知識.在第三節,構造方程(2)和方程(3)所允許的李代數和相應的一維優化系統.在第四節,基于第三節得到的優化系統,對方程(2)和方程(3)進行對稱約化并計算相應的群不變解,并用數學軟件Matlab畫出時空分數階方程(2)的精確解的三維圖.在第五節建立方程(2)的守恒律.在最后一節給出本文的總結.

2 基礎知識

本節給出分數階Riemann-Liouville導數的定義和李對稱分析的步驟.

定義2.1設n∈N.則α階Riemann-Liouville導數的定義為當0＜n-1＜α＜n時.其中為通常的n階偏導數,為伽馬函數.下面考慮一般的時空分數階偏微分方程

假定單參數Lie群變換為

其中ηα,t,ηβ,x,ηxx的定義為

Dx和Dt是關于x和t的全導數且定義為

設方程(4)的無窮小生成子為

其中

無窮小生成子(8)所對應的向量場能生成方程(4)的一個對稱當且僅當方程(4)的向量場V滿足以下不變準則

延拓算子Pr(α,2)V定義為

其中ηα,t,ηβ,x,ηx和ηxx分別滿足(6)式-(7)式.

此外,基于不變準則(10),時空分數階偏微分方程(4)還需滿足以下初始條件

引理2.1[5]設α＞0,0.當α+β＜1且2α+β＜1時,如下分數階微分方程有精確解

3 李對稱和一維優化系統

本節將利用對稱分析方法計算出方程(2)和方程(3)所允許的李代數及相應的一維優化系統.

3.1 方程(2)的李對稱和優化系統

本節利用對稱分析法來推導方程(2)的李代數,再由李代數構造出方程(3)的一維優化系統.

定理3.1時空分數階方程(2)的李代數l1由以下向量場張成

證明將方程(2)代入不變準則(10),可以得到方程(2)的不變方程為

將(6)式代入(14)式,并使方程中線性無關的u的各階導數的系數等于零可以得到以下決定方程組

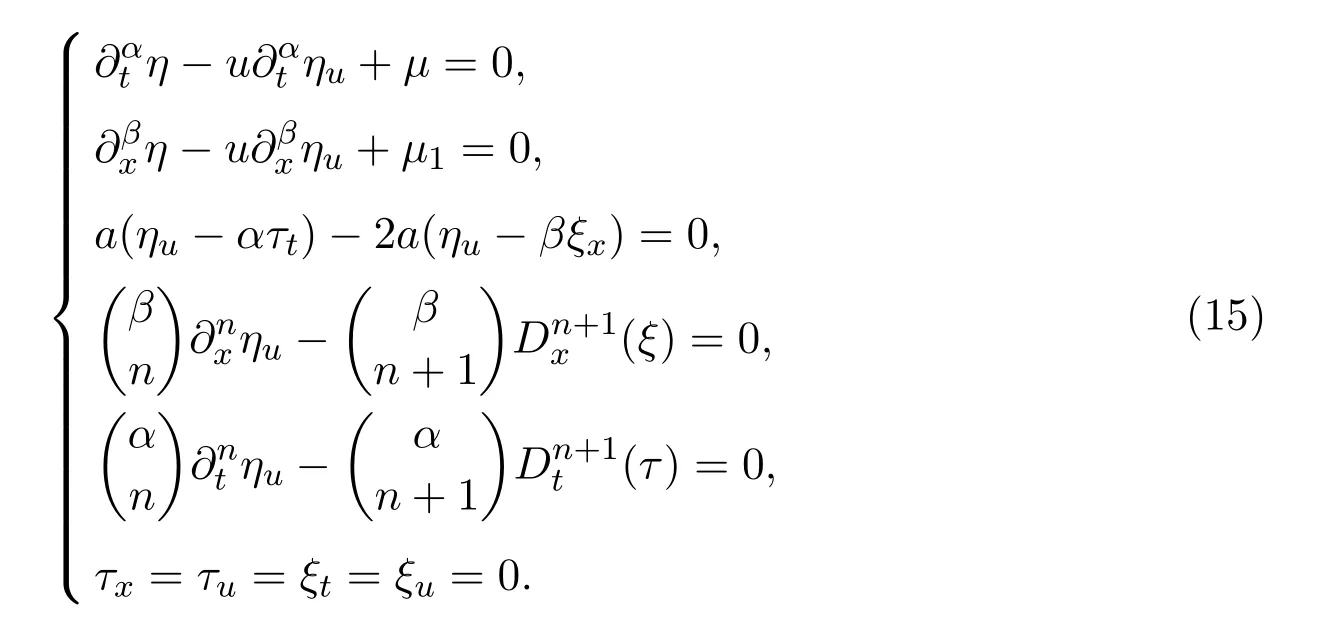
求解決定方程組(15)可得

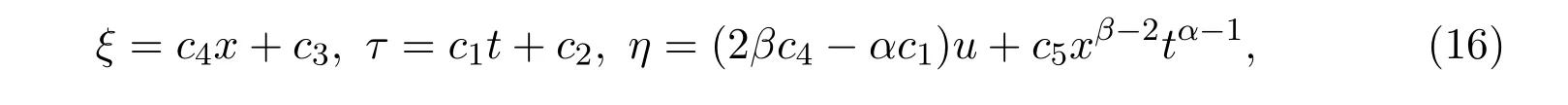
其中ci(i=1,2,3,4,5)是任意常數.根據不變條件(10)可以推出c2=c3=0.

由此可證方程(2)的對稱群為(13).下面來計算李代數l1的一維優化系統.

通過計算得到李代數l1的非零交換子為

另外,伴隨算子的作用由以下李級數給出

其中?為任一參數.根據上式,能夠推導出李群G1對李代數l1的伴隨作用,如表1所示.按照文獻[21]介紹的方法,可以得到李代數l1關于時空分數階α,β的一維優化系統,結果在下述定理給出,這里省略其證明過程.

表1 向量場(15)的伴隨表示

定理3.2(1)對于李代數l1的一維優化系統為

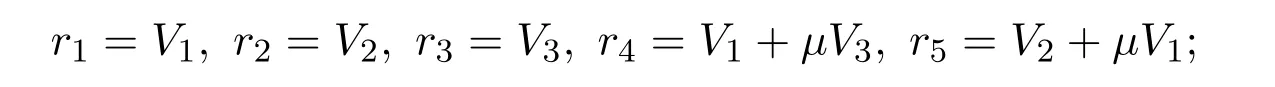
3.2 方程(3)的李對稱和優化系統

本小節將利用對稱分析構造方程(3)所允許的李代數和相應的一維優化系統.

定理3.3時間分數階方程(3)的李代數l2由以下向量場張成

證明將方程(3)代入不變準則(10),可得

把(6)式代入(19)式,并令u的各階線性無關導數的系數等于零,化簡后可以得到以下決定方程組

求解決定方程組(20)可得

其中ci(i=1,2,3,4,5)是任意常數.此外,由初始條件(12)可以推出c2=c3=0,即證方程(3)的李代數(18).

容易看出向量場V1和V3是伸縮算子,V2是平移算子,李代數(18)的非零交換子為

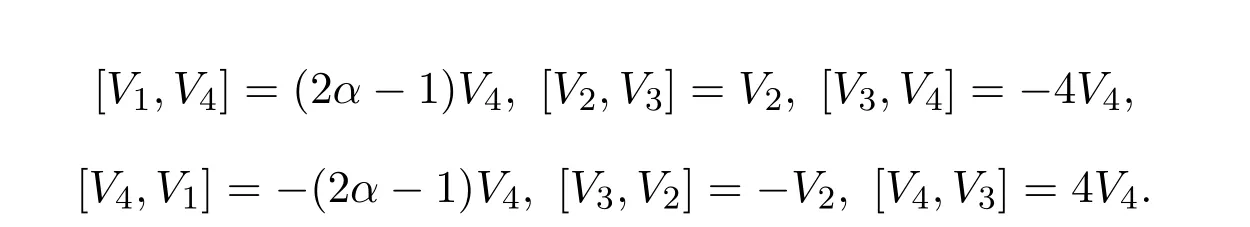
進一步地,由伴隨算子的定義(17)可以推導出李群G2對李代數l2的伴隨作用,如表2所示.

表2 向量場(17)的伴隨表示

與前一小節類似,按照文獻[21]介紹的方法可以得到以下定理.

定理3.4(1)對于和μ∈R,李代數l2的一維優化系統為

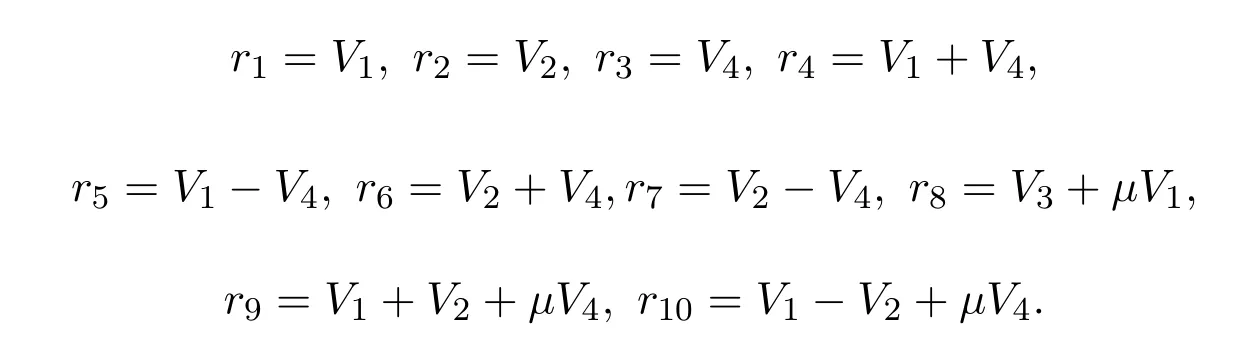
4 對稱約化和群不變解

本節利用定理3.2和定理3.4所得到的結果,對方程(2)和方程(3)做對稱約化并構造相應的群不變解,并給出群不變解的圖像.

4.1 方程(2)的對稱約化和群不變解

本小節利用定理3.2得到的一維優化系統,將復雜的非線性時空分數階微分方程約化為較為簡單的分數階常微分方程,約化后的分數階常微分方程將更容易求解.下面介紹定理3.2中一維優化系統對應的對稱約化和群不變解.

對于方程(2)有以下情形成立.

情形1:r1=t?t-αu?u.對應的特征方程為

計算特征方程(22)可得方程(2)的兩個不變量為x和utα,從而方程(2)有如下形式的群不變解

情形2:r2=x?x+2βu?u.對應特征方程為

計算方程(25)可知方程(2)有如下形式的群不變解

將(26)式代入方程(2)可得

將(27)式代回(26)式得到方程(2)的一個精確解為

對于(28)式,通過數學軟件Matlab繪制如下圖1三維圖像解.

圖1 u1(x,t)的三維圖像.

在圖1(a)和圖1(b)中,取a=-1,β=1.5,可以觀察到隨著時間分數階導數的階數α的增大,u1(x,t)逐漸減小,當t趨于零時,曲率逐漸增大.在圖1(c)和圖1(d)中,取a=-1,α=0.4,可以觀察到隨著空間分數階導數的階數β的增大,u1(x,t)也增大,當x趨于零時,曲率逐漸減小.在圖1(e)和圖1(f)中,取α=0.3,β=1.5,可以觀察到參數a對精確解u1(x,t)的影響.

4.2 方程(3)的對稱約化和群不變解

本小節利用定理3.4中得到的一維優化系統,將復雜的非線性時間分數階微分方程約化為較為簡單的常微分方程,約化后的常微分方程更容易求解.下面介紹定理3.4中方程(3)的對稱約化和群不變解.

對于方程(3)有以下情形成立.

情形1:r1=t?t-αu?u.r1對應特征方程為

計算特征方程(29)得方程(3)的群不變解為u(x,t)=t-αf(x),f(x)滿足如下常微分方程(當時)

情形2:r2=?x.計算r2對應特征方程得到群不變解為u(x,t)=g(t),代入方程(3)得到(t)=0,計算得到g(t)=ktα-1,其中k為任意常數.從而方程(3)的一個群不變解如下

情形3:r4,5=±?x+t?t-αu?u.r4對應的特征方程如下

計算(31)式,得到方程(3)的一個群不變解為

其中f(z)(z=te?x)滿足如下分數階常微分方程

情形4:r6,7=?x±tα-1?u.r6的特征方程為

解特征方程(32)可以得到方程(3)有如下群不變解

將(33)式代回方程(3)得g(t)=ktα-1.因此,方程(3)的精確解為

5 守恒律

本節在李代數(13)的基礎上,建立時空分數階方程(2)的守恒律.

方程(2)的守恒向量C=(Ct,Cx)滿足如下守恒律

其中Ct=Ct(t,x,u,···),Cx=Cx(t,x,u,···).

方程(2)的拉格朗日形式如下

其中v(x,t)為新的因變量.歐拉-拉格朗日算子有如下形式

由(36)式可以得到方程(2)的伴隨方程為

取v(x,t)=φ(x,t,u),得到如下方程

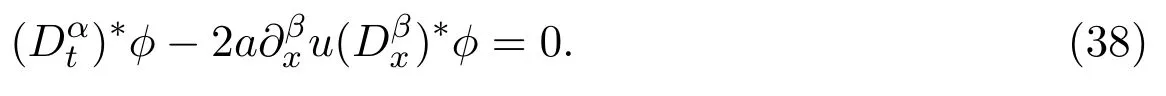
解(38)式得到

其中A為任意常數.

下面將通過以下公式分別建立守恒向量t,x的分量

其中n=[α]+1,m=[β]+1,Wi=ηi-ξiux-τiut,J,J1定義為

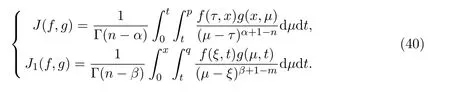
結合向量場(13),可以得到以下特征方程

取A=1,可以得到以下結論:

當0＜α＜1,1＜β＜2時,方程(2)的t分量的守恒向量為

當0＜β＜1,0＜α＜1時,方程(2)的x分量的守恒向量為

當1＜β＜2,0＜α＜1時,方程(2)的x分量的守恒向量為

6 結論

本文研究了李對稱分析在時空分數階微分方程的應用,并以一類廣義時空分數階雙多孔介質方程為例,計算了它所允許的李代數并建立了優化系統.進一步地對方程(2)和方程(3)進行了對稱約化,在此基礎上得到方程(2)的精確解u0,u1,方程(3)的精確解u2,u3,u4,并用數學軟件畫出方程(2)的精確解u1(x,t)的三維圖像.最后,利用定理3.1的結論和新Noether定理構造了方程(2)的守恒律.