考慮原產(chǎn)地規(guī)則的跨境紡織供應鏈網(wǎng)絡(luò)設(shè)計
茅 茂, 王長軍
(東華大學 旭日工商管理學院, 上海 200051)
近年來,一方面,經(jīng)濟的全球化趨勢促使包括紡織企業(yè)在內(nèi)的中國制造企業(yè)展開跨境布局,以獲得原料、生產(chǎn)及市場等要素的全球配置;另一方面,隨著國內(nèi)勞動力等各項成本的不斷攀升,也促使制造企業(yè)“走出去”。在如上的外部和內(nèi)部因素驅(qū)動下,我國紡織企業(yè)的供應鏈網(wǎng)絡(luò)全球化也已成為趨勢[1],但是,跨境布局的企業(yè)卻面臨著貿(mào)易制度安排帶來的挑戰(zhàn)和機遇。在阻礙跨境貿(mào)易的眾多制度中,原產(chǎn)地規(guī)則是需要被重點關(guān)注的一項[2],它會造成跨境貿(mào)易中關(guān)稅差別對待,這迫使企業(yè)為規(guī)避貿(mào)易管制措施,改變自身的供應鏈安排[3],從而,在一定程度上改變了全球供應鏈的布局。注意到這樣的貿(mào)易管制措施會對全球供應鏈造成的復雜影響,經(jīng)濟聯(lián)系緊密的國家會考慮聯(lián)合起來,通過達成大型區(qū)域貿(mào)易協(xié)定,以新的制度安排,以規(guī)范貿(mào)易障礙對全球供應鏈利益實現(xiàn)帶來的干擾[4]。其中,最具有代表性的就是2020年底簽署的《區(qū)域全面經(jīng)濟伙伴關(guān)系協(xié)定》(RCEP協(xié)定)[5]。該協(xié)定由東盟發(fā)起,中、日、韓、澳及新西蘭等15個國家簽署加入。為減少域內(nèi)企業(yè)的貿(mào)易壁壘,RCEP協(xié)定中最重要的突破之一便是制定更為靈活自由的區(qū)域累積原產(chǎn)地規(guī)則,即產(chǎn)品增值部分只要屬于成員國,且累積增值超過40%,便可視為原產(chǎn)地產(chǎn)品,享有關(guān)稅免除。而考慮到協(xié)定實施后可覆蓋全球近一半人口和近三分之一的貿(mào)易量,相關(guān)制度安排將顯著改變世界貿(mào)易格局[6]。我國已完成RCEP的核準[7]。RCEP于2022年1月1日起包括中國、日本、泰國、新加坡在內(nèi)的10個國家正式生效。由此,對于跨境布局的企業(yè),特別是以東南亞為主要布局區(qū)域的紡織企業(yè)[8]而言,如何在新的貿(mào)易規(guī)則安排下,實現(xiàn)對自身的跨境供應鏈網(wǎng)絡(luò)規(guī)劃,是相關(guān)企業(yè)“走出去”面臨的緊迫問題,也是本文的研究重點。
國內(nèi)外已有不少學者在全球供應鏈網(wǎng)絡(luò)優(yōu)化決策領(lǐng)域開展了相關(guān)研究。其中,早期研究起源于Hodder和Jucker[9]對全球工廠的選址問題研究。之后,Cohen和Lee[10]將其擴展為多階段全球供應鏈布局模型。之后,引發(fā)了關(guān)于跨境選址-配送的大量研究,例如Christina等[11]研究了跨境的工廠以及配送中心的選址,及其之間的運輸決策。Cohen和Lee[12]、Boujelben和Boulaksila[13]對相關(guān)研究進行了綜述。在這些工作基礎(chǔ)上,有學者從不同角度對經(jīng)典選址-配送模型進行了擴展,其中,有相當多的研究考慮了跨境交易過程中的關(guān)稅問題。如Wilhelm等[14]以北美自由貿(mào)易協(xié)定下美墨貿(mào)易展開研究,提出了一個混合整數(shù)規(guī)劃模型解決關(guān)稅影響下的供應鏈網(wǎng)絡(luò)決策。汪傳旭[15]考慮優(yōu)化多階段全球供應鏈網(wǎng)絡(luò),旨在實現(xiàn)基礎(chǔ)設(shè)施成本、生產(chǎn)成本、關(guān)稅成本等之和最小。Boujelben等[13]則綜合考慮了關(guān)稅、匯率、轉(zhuǎn)移價格等因素。
但是,現(xiàn)有研究還存在一定的局限性。首先,考慮原產(chǎn)地規(guī)則的研究極少。文獻[16]是為數(shù)不多的將原產(chǎn)地規(guī)則引入全球供應鏈網(wǎng)絡(luò)優(yōu)化的研究,但該研究只是考慮了原產(chǎn)地規(guī)則對原材料和產(chǎn)成品進出口配額的影響,并沒有考慮相應的關(guān)稅代價,以及企業(yè)如何通過供應鏈布局來規(guī)避對其不利的規(guī)則。更沒有工作針對RCEP協(xié)定中區(qū)域累積規(guī)則帶來的影響展開研究。其次,近年來,針對特定行業(yè)的研究引發(fā)了廣泛的關(guān)注,如液氮[17]、有色金屬[18]等,但針對紡織企業(yè)的全球供應鏈網(wǎng)絡(luò)優(yōu)化的研究還極為有限。
綜上,本文針對紡織行業(yè),研究跨境供應鏈網(wǎng)絡(luò)優(yōu)化決策。其中,在供應鏈網(wǎng)絡(luò)優(yōu)化方面,綜合考慮多種紡織原料下的供應商選擇、工廠選址、產(chǎn)能規(guī)劃,以及采購、生產(chǎn)和運輸決策;在跨境貿(mào)易因素上,重點關(guān)注原產(chǎn)地規(guī)則的影響,以及RCEP協(xié)定下的區(qū)域累積規(guī)則帶來的影響。為此,提出了一個新的考慮原產(chǎn)地規(guī)則的混合整數(shù)規(guī)劃模型。然而,由于原產(chǎn)地規(guī)則的考慮,使得構(gòu)建模型為非線性。為最優(yōu)求解,將其線性化為等價的線性模型,并設(shè)計了基于Benders分解的求解算法。最后,將模型應用于某紡織企業(yè)在東南亞建設(shè)面料生產(chǎn)線的決策上,通過對不考慮原產(chǎn)地規(guī)則、非區(qū)域累積的原產(chǎn)地規(guī)則和區(qū)域累積的原產(chǎn)地規(guī)則3種情況的對比,驗證本文研究的有效性并得到相關(guān)管理結(jié)論。
1 跨境紡織供應鏈網(wǎng)絡(luò)模型構(gòu)建
1.1 問題描述
本文考慮由分布在不同國家的供應商、工廠和分銷商組成的3級紡織供應鏈網(wǎng)絡(luò),如圖1所示。其中,供應商提供生產(chǎn)所需的棉紗、滌綸、氨綸等紡織基礎(chǔ)原料,工廠按給定的物料消耗表(bill of material, BOM)生產(chǎn)面料,并為全球的分銷商提供產(chǎn)成品。為解決中國紡織企業(yè)“走出去”戰(zhàn)略面臨的相關(guān)決策問題,研究以工廠為主體,考慮其面臨的工廠選址、產(chǎn)能規(guī)劃、供應商選擇、原料采購、產(chǎn)成品生產(chǎn)以及供應鏈網(wǎng)絡(luò)各節(jié)點間的運輸決策。
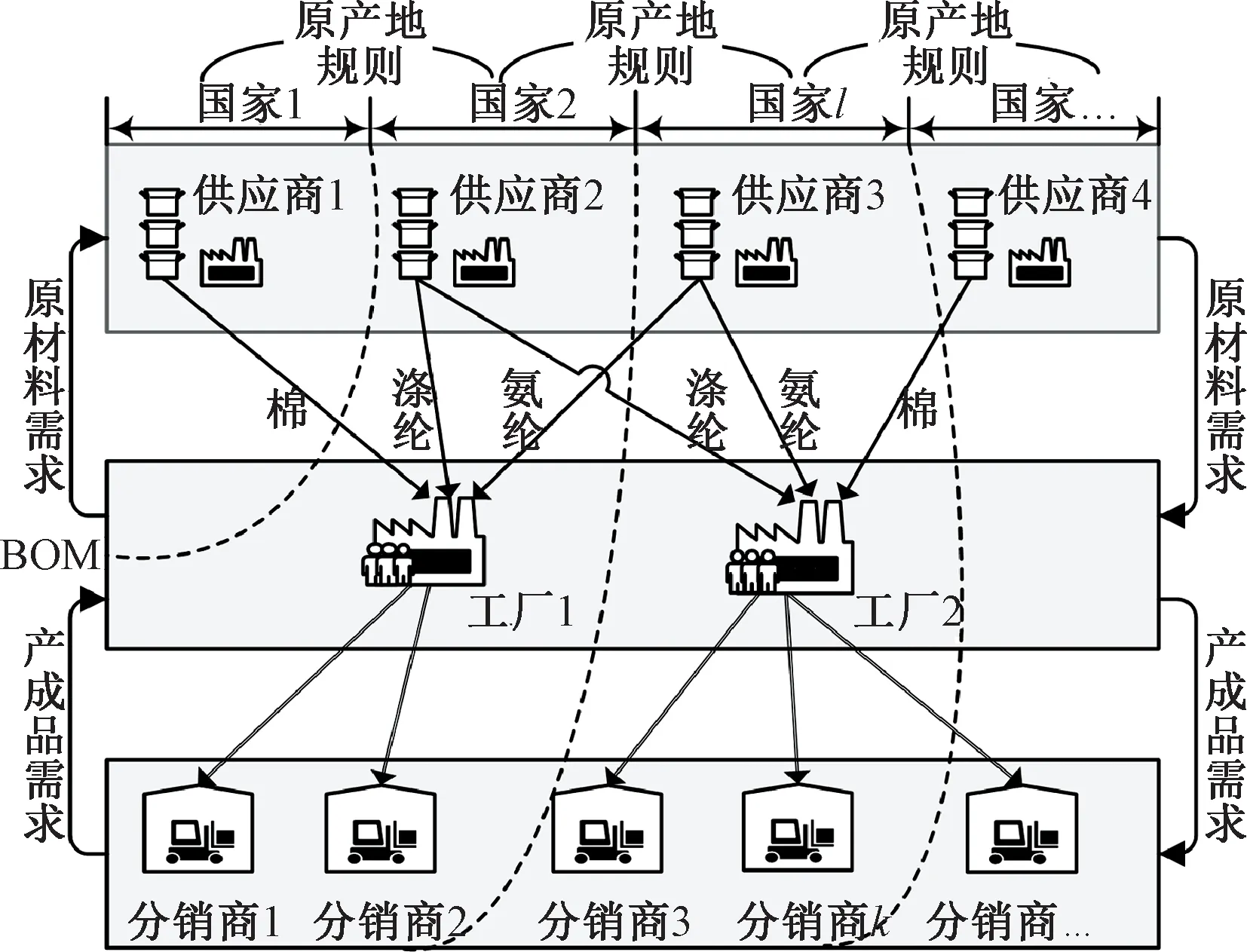
圖1 跨境紡織供應鏈網(wǎng)絡(luò)圖
研究中特別考慮了原產(chǎn)地規(guī)則帶來的影響。其中,采用基于增值百分比標準的原產(chǎn)地規(guī)則,即以某國家或地區(qū)對貨物進行加工制造時,貨物發(fā)生的價值增值(包括原材料、勞動力的價值以及其他資本價值的投入)不低于規(guī)定的比例α時,該貨物的生產(chǎn)地才能被認定為該國家或者地區(qū)。令a為貨物最終價值,b為非某國的材料價值,c為不明原產(chǎn)地的材料價值,原產(chǎn)地規(guī)則的概念公式可表達為
而RCEP采用的是更為友好的區(qū)域累積原產(chǎn)地規(guī)則,只要在15個成員國內(nèi)的總價值增量不低于規(guī)定的比例40%時,便可認定為原產(chǎn)地貨物,享有優(yōu)惠關(guān)稅。
綜上,擬構(gòu)建相應的優(yōu)化模型解決上述相關(guān)決策,模型以利潤最大化,即銷售收入減去成本為目標。其中,成本包括工廠選址、產(chǎn)能建設(shè)、供應商選擇、原料采購、生產(chǎn)、運輸、缺貨懲罰,以及受原產(chǎn)地規(guī)則支配的關(guān)稅。
然而,由于原產(chǎn)地規(guī)則的考慮,導致所建模型為非線性。為實現(xiàn)對模型的最優(yōu)求解,需對其進行線性化。為此,本文首先給出相關(guān)參數(shù)和變量說明;繼而構(gòu)建混合整數(shù)非線性規(guī)劃模型,并將模型線性化;針對線性化后模型設(shè)計基于Benders分解的最優(yōu)求解算法;最后將研究應用于實際問題的解決中,以展現(xiàn)其有效性。
1.2 變量說明
建模所需的集合、參數(shù)和決策變量如表1~3所示。

表1 集合說明

表2 參數(shù)說明

表3 決策變量說明
1.3 模型構(gòu)建
構(gòu)建考慮原產(chǎn)地規(guī)則的跨境紡織供應鏈網(wǎng)絡(luò)模型,以企業(yè)利潤最大化為目標。目標函數(shù)可大致分為銷售收入、供應鏈布局成本、供應鏈運營成本以及關(guān)稅成本4個部分。具體來說,銷售收入為
P=∑j∑l∑k∑l′Vjlkl′·pjl
(1)
供應鏈布局成本包括了工廠選址與建設(shè)、供應商選擇的代價:
(2)
供應鏈運營成本,包括了原料采購、生產(chǎn)、缺貨、運輸成本:
C2=∑m∑i∑lcmil·(∑j∑l′Qmiljl′)+
∑j∑lgjl·Gjl+∑k∑lskl·Skl+
∑i∑l∑j∑l′∑mqmiljl′·Qmiljl′+
∑j∑l∑k∑l′vjlkl′·Vjlkl′
(3)
關(guān)稅的費用為
(4)
綜上,供應鏈設(shè)計的優(yōu)化目標可表示為
(5)
同時滿足如下約束:
∑j∑l′Qmiljl′≤hmil·Xil?i,?m,?l
(6)
∑m∑i∑lQmiljl′≤M·Yjl′?j,?l′
(7)
∑k∑l′Vjlkl′≤M·Yjl?j,?l
(8)
∑l″Amiljl′l″≤Qmiljl′?m,?i,?l,?j,?l′
(9)
Gjl≤Ujl?j,?l
(10)
∑k∑l′Vjlkl′≤Gjl?j,?l
(11)
Skl′+∑j∑lVjlkl′=dkl′?k,?l′
(12)
(13)
rl″l′(∑m∑i∑lcmil·Amiljl′l″+gjl′·∑kVjl′kl″)≤
∑m∑i∑l=l′cmil·Amiljl′l″+gjl′·
∑kVjl′kl″+(1-Rjl′l″)·M?j,?l′,?l″
(14)
∑m∑i∑l=l′cmil·Amiljl′l″+gjl′·∑kVjl′kl″≤
rl″l′(∑m∑i∑lcmil·Amiljl′l″+gjl′·∑kVjl′kl″)+
Rjl′l″·M?j,?l′,?l″
(15)
Ujl,Gjl,Qmiljl′,Amiljl′l″,Vjlkl′,Skl≥0
?m,?i,?l,?j,?l′,?k,?l″
(16)
Rjll′,Xil,Yjl∈{0,1} ?i,?l,?j,?l′
(17)
其中:式(6)為原材料供應與供應商選擇的約束,即若供應商未被選中,則不能提供原材料;若選中,提供的原材料數(shù)量不能超過其產(chǎn)量約束;式(7)為原材料采購與工廠選址約束,其中M為一足夠大正數(shù),表示若l′國某工廠j不被選擇則不進口原材料,被選擇時則進口原材料;式(8)為產(chǎn)成品出口與工廠選址約束,若l′國某工廠j不被選中,則無法向分銷商運輸產(chǎn)品,若選中則可運輸產(chǎn)品;式(9)為生產(chǎn)使用的原材料數(shù)量的約束,l′國某工廠j使用的來自l國某供應商i的某原材料m的數(shù)量不得超過該工廠從l國某供應商i進口的該原材料的數(shù)量;式(10)為工廠產(chǎn)能約束;式(11)表示運輸量與產(chǎn)量約束;式(12)表示運量、需求和缺貨數(shù)平衡約束;式(13)表示產(chǎn)成品和原料使用量約束;式(14)、(15)判斷產(chǎn)成品是否滿足原產(chǎn)地規(guī)則要求。當l′國某工廠生產(chǎn)的產(chǎn)成品滿足l″國的原產(chǎn)比例要求時,Rjl′l″取值為1,否則,取值為0。式(16)和(17)是對決策變量取值的約束。
1.4 模型等價轉(zhuǎn)化
在上述模型中,由于原產(chǎn)地規(guī)則的考慮,使得模型目標函數(shù)中的式(4)出現(xiàn)了非線性項,即決策變量Rjll′和Vjlkl′的乘積。為對其線性化,引入輔助變量,用于表示某工廠出口至l″國的產(chǎn)成品由于不滿足原產(chǎn)地規(guī)則而需繳納的關(guān)稅額,即
此時,式(4)可表述為
(18)
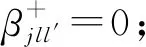
?j,?l,?l′
(19)
(20)
1.5 基于Benders分解的算法設(shè)計
所建模型中包含了大量難求解的0~1變量,也存在如采購量、運輸量、產(chǎn)量、缺貨量等線性變量。為對其最優(yōu)求解,考慮采用Benders分解[19]。該方法可用于解決大規(guī)模混合整數(shù)規(guī)劃模型。其核心是根據(jù)變量類型的不同,將模型分解為只含有整數(shù)變量(也稱復雜變量)的主問題和包含連續(xù)變量的子問題,以降低求解難度。并通過主子問題的迭代求解獲得模型的最優(yōu)結(jié)果。Benders分解自提出以來,就被廣泛應用于各種場景的大規(guī)模問題求解中[20]。
為將Benders分解用于本文問題的求解中,將線性化后模型分解為主問題和子問題。首先,構(gòu)建僅保留線性變量的子問題如下:
∑m∑i∑lcmil(∑j∑l′Qmiljl′)+
∑i∑lgjlGjl+∑m∑i∑l∑j∑l′qmiljl′Qmiljl′+
∑j∑l∑k∑l′vjlkl′Vjlkl′+∑k∑lsklSkl+
(21)
服從于式(6)~(15),(19),(20)。其中,整數(shù)變量可由主問題計算給出,是已知的,因此,子問題為標準線性規(guī)劃。繼而,由子問題,構(gòu)造向主問題添加的最優(yōu)Benders割,如式(22)所示:
(22)
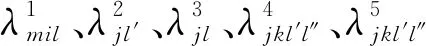
由此,可構(gòu)造主問題模型為
服從于式(22)
Xil、Yjl、Rjll′∈{0,1} ?i,?l,?j,?l′
(23)
其中,式(22)為添加的最優(yōu)割。由于本文允許缺貨,即需求可不被滿足,故而子問題總有可行解。所以無需向主問題添加可行割。
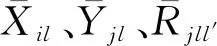
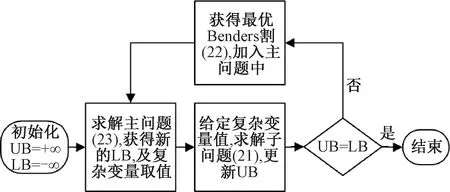
圖2 Benders分解算法流程圖
2 算例仿真與分析
2.1 仿真參數(shù)
本文考慮某紡織企業(yè)主要生產(chǎn)滌/棉/氨混紡面料。主打面料產(chǎn)品面密度為0.23 kg/m2,其中,滌綸(T)含量為62%,棉(C)為33%,氨綸(SP)為5%,具有良好的柔軟性和透氣性。由于東南亞地區(qū)與中國地理位置接近,且勞動力價格低、土地價格相對便宜,因而受到很多勞動密集型企業(yè)的青睞[8]。該企業(yè)為了能夠享有東南亞地區(qū)的生產(chǎn)成本優(yōu)勢以及貿(mào)易協(xié)定優(yōu)惠等,考慮將生產(chǎn)工廠布局至相關(guān)地區(qū)。
考慮10個工廠待選點,分別在越南(VIE)、緬甸(MYA)、印度尼西亞(INA)、泰國(THA)、柬埔寨(CAM)。該企業(yè)將在中國(CHN)、印度(IND)、澳大利亞(AUS)、越南和緬甸挑選棉紗供應商;在中國、印度、韓國(PRK)、日本(JPN)、印度尼西亞和泰國挑選滌綸和氨綸絲的供應商。生產(chǎn)的產(chǎn)成品將出口至中國、韓國、日本、印度尼西亞、泰國、越南、柬埔寨、緬甸和老撾(LAO),每個國家分別有2個分銷商。產(chǎn)成品單位售價以美元計為9.6美元/kg。單位質(zhì)量單位距離的運費為0.262美元/(1 kg·1 000 km)。假設(shè)運輸成本與運輸距離呈正比,供應鏈中各節(jié)點間的距離根據(jù)谷歌地圖近似估算而得。其余相關(guān)數(shù)據(jù)如表4~6所示。表中縮寫代表國家名,不同供應商用括號加數(shù)字區(qū)分,工廠用下劃線加數(shù)字區(qū)分。
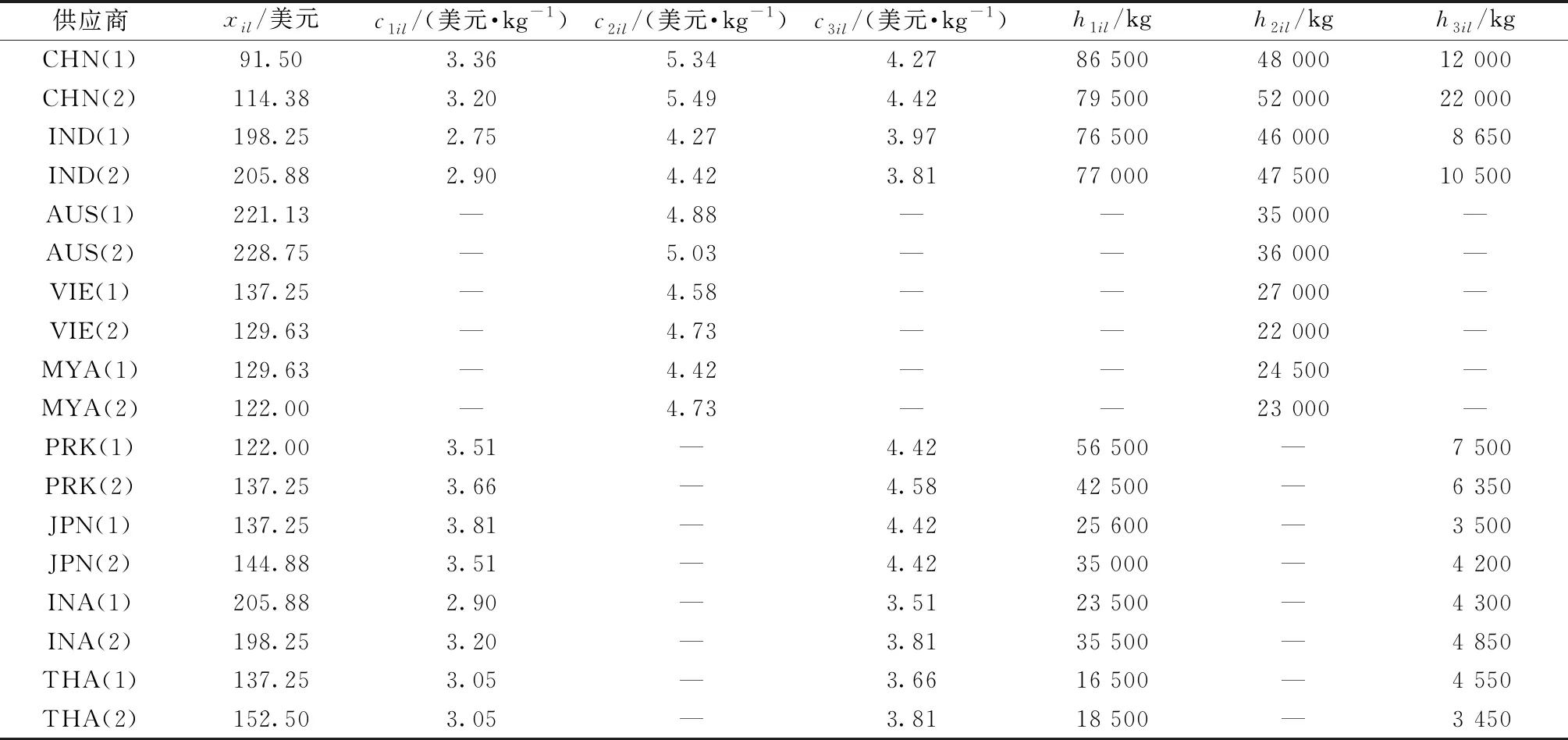
表4 供應商相關(guān)數(shù)據(jù)(選擇成本、原材料價格、供貨能力)
2.2 仿真結(jié)果
針對如下3種場景展開仿真:1)不存在關(guān)稅減免,所有貨物交易按照現(xiàn)行關(guān)稅執(zhí)行;2)采用非區(qū)域累積的原產(chǎn)地規(guī)則,實現(xiàn)的增值部分屬于當?shù)厍页^40%,可視為原產(chǎn)地產(chǎn)品,享受關(guān)稅免除;3)考慮RCEP協(xié)定中的區(qū)域累積原產(chǎn)地規(guī)則,即實現(xiàn)增值部分屬于域內(nèi)國家且累積超過40%,即可視為原產(chǎn)地產(chǎn)品,享受關(guān)稅免除[21]。
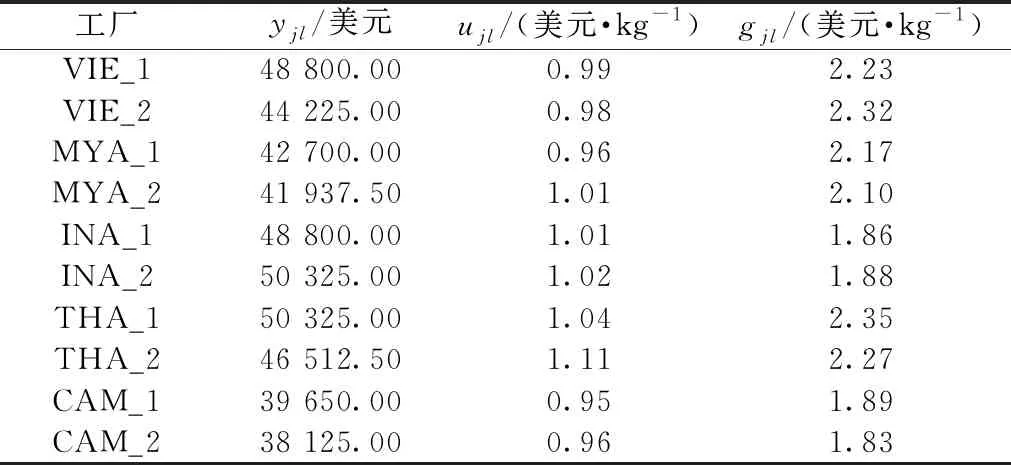
表5 工廠相關(guān)數(shù)據(jù)(選擇成本、建設(shè)成本、生產(chǎn)成本)
在主頻為2.6 GHz,內(nèi)存為8 GB的筆記本電腦上,利用Visual Studio C++實現(xiàn)Benders分解算法。其中,算法迭代中的主子問題最優(yōu)求解通過調(diào)用求解器ILOG CPLEX12.5實現(xiàn)。由此,得到3種場景的最優(yōu)結(jié)果如表7所示。其中,工廠布局成本包括選擇工廠的固定成本以及建設(shè)成本;采購成本包括原材料采購以及供應商選擇成本;運輸成本包括原材料以及產(chǎn)成品的運輸成本。原材料采購量如表8所示,未被選中的供應商不在此表中顯示。
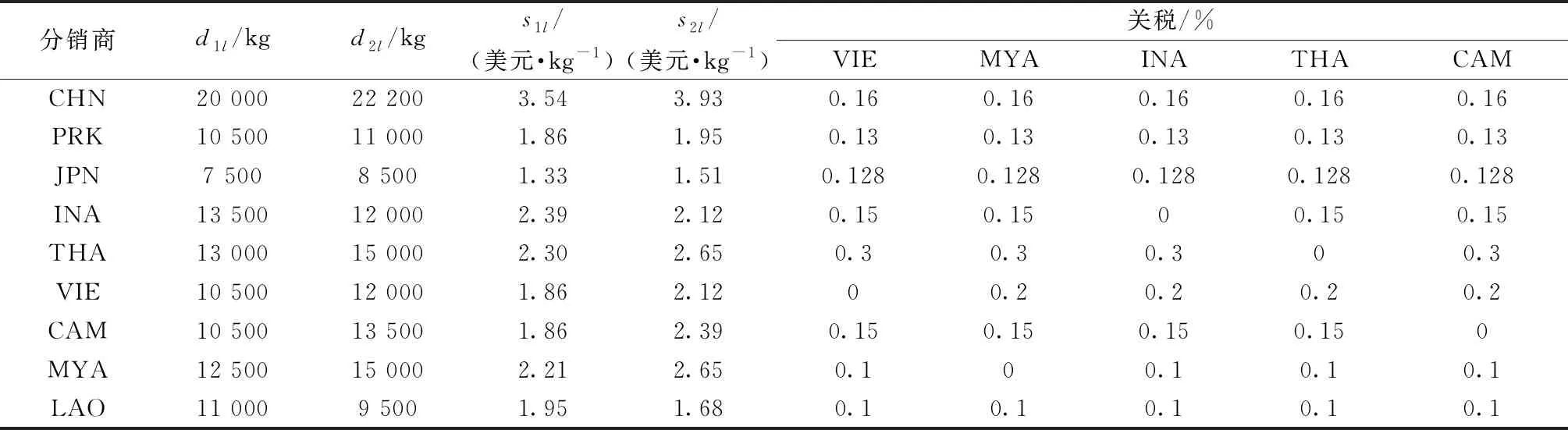
表6 分銷商相關(guān)數(shù)據(jù)(需求、缺貨成本、關(guān)稅)
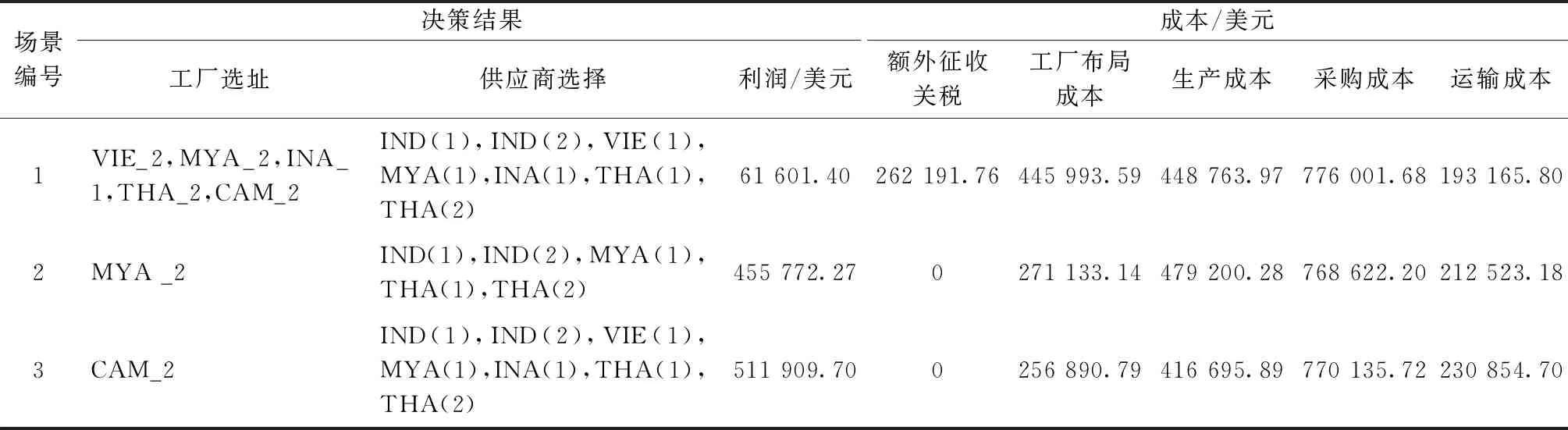
表7 不同場景下的最優(yōu)解及最優(yōu)決策
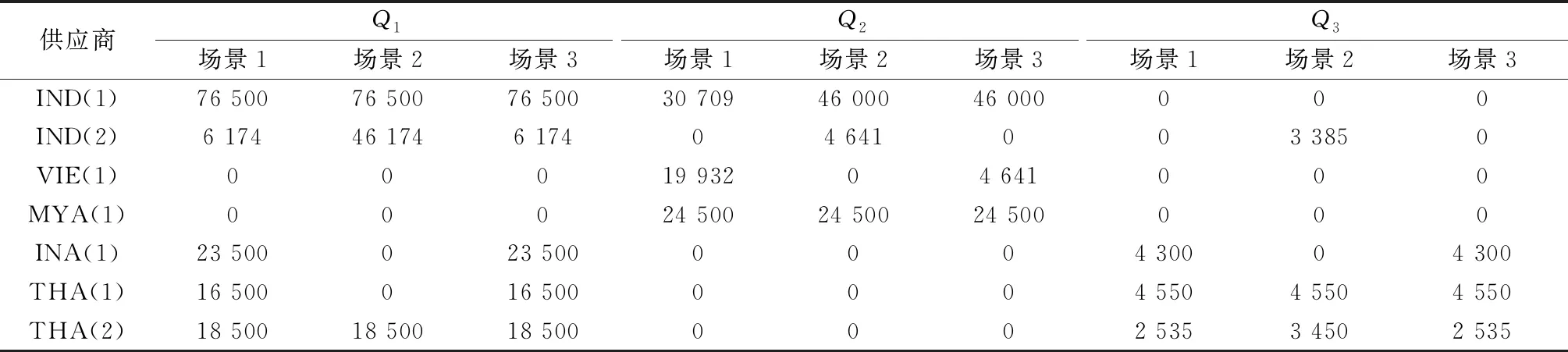
表8 不同場景下的原材料采購決策
通過上述的仿真結(jié)果發(fā)現(xiàn),首先,在不考慮原產(chǎn)地規(guī)則的情況下,即場景1,不存在相應的關(guān)稅減免。為盡可能降低關(guān)稅帶來的影響,在本文中,企業(yè)不得不在分銷商,即主要市場所在的國家選建工廠(見表7)。顯然,這會導致工廠布局成本增加,從而造成利潤下降。
其次,在非區(qū)域累積的原產(chǎn)地規(guī)則下,優(yōu)惠關(guān)稅的存在會在一定程度上促進出口貿(mào)易,但原產(chǎn)地規(guī)則是基于特定國家的增值。顯然,這會促使企業(yè)集中布局到具有產(chǎn)業(yè)集聚優(yōu)勢的國家,即該國同時具有較有競爭力的供應商和工廠待選點。由此,最終選擇了工廠待選點MYA_2,同處一國的供應商MYA(1)也被選擇,并產(chǎn)生了較大的采購量(見表7)。基于這些決策,實際生產(chǎn)的產(chǎn)成品實現(xiàn)了47%的原產(chǎn)比例,滿足40%的政策要求。
第三,RCEP實施的是區(qū)域累積的原產(chǎn)地規(guī)則,即關(guān)注的增值是發(fā)生于RCEP成員國。顯然,這一政策改變將賦予企業(yè)更為自由的選址及生產(chǎn)采購決策空間,更有利于實現(xiàn)全球供應鏈的最優(yōu)配置。仿真結(jié)果也驗證了這一點。具體來說,工廠選址于更具有成本優(yōu)勢的CAM_2。而該工廠所在地由于缺乏有競爭力的供應商,在場景2中是不會被選擇的。此外,供應商選擇則可綜合其地理位置和供應商自身競爭力在域內(nèi)國家自由布局,見表7。特別應當注意到,這一決策方案在場景2下,實際生產(chǎn)的產(chǎn)成品只能到達35%的原產(chǎn)比例,無法滿足關(guān)稅減免的條件。而在區(qū)域累積規(guī)則下,則可實現(xiàn)64%的原產(chǎn)比例。
此外,有必要說明,為與場景3中的基于區(qū)域累積的原產(chǎn)地規(guī)則作對比,場景2構(gòu)造非區(qū)域累積的原產(chǎn)地規(guī)則,并假設(shè)所有國家均設(shè)定原產(chǎn)比例40%。這一假設(shè)與實際情況不完全一致。為此,下文對場景2的原產(chǎn)比例要求展開靈敏度分析。通過變化這一比例要求,得到企業(yè)利潤與各工廠出口產(chǎn)成品達成的原產(chǎn)比例的平均值,如圖3所示。
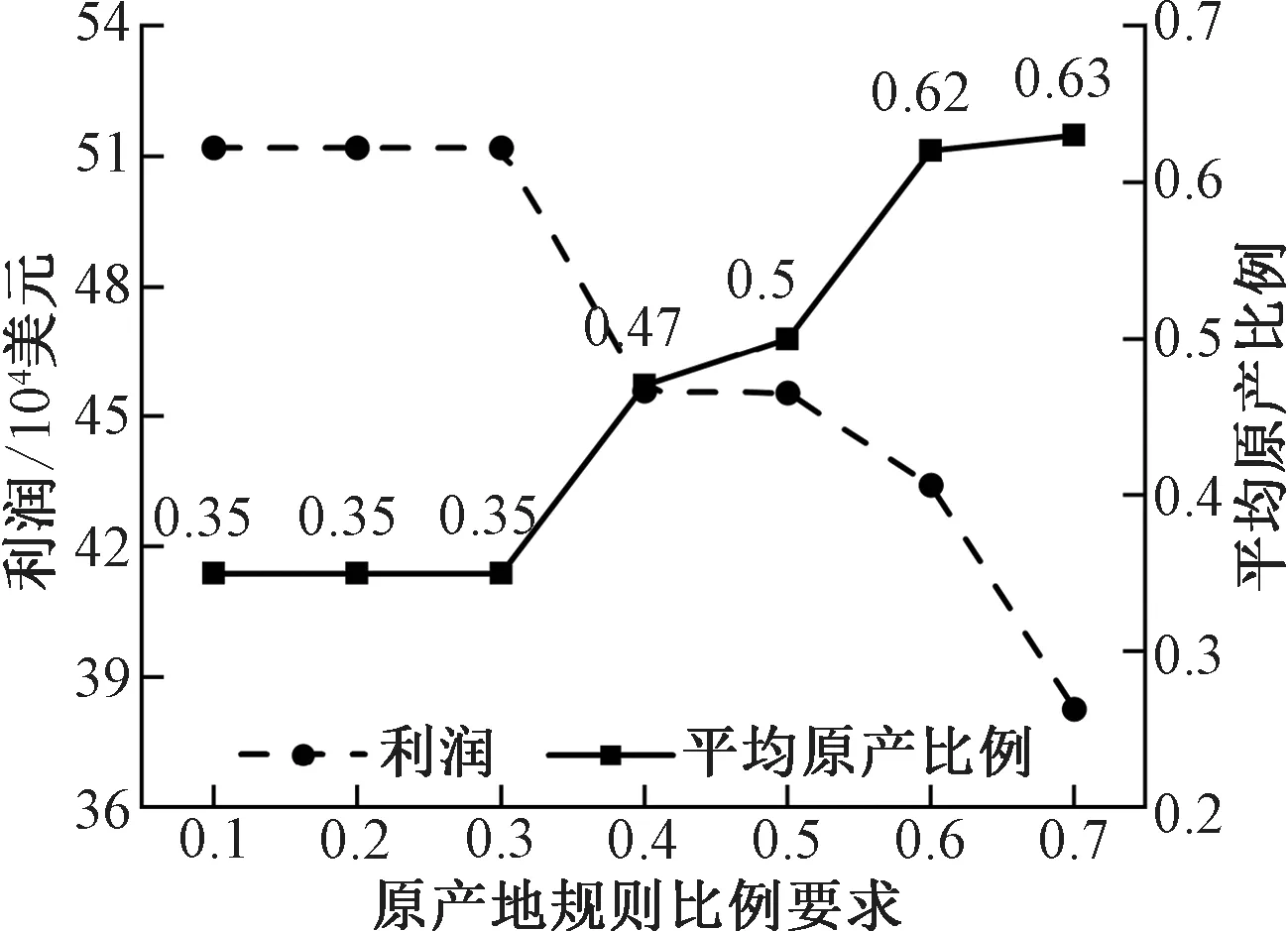
圖3 基于原產(chǎn)地規(guī)則比例要求的靈敏度分析
由圖3可知,隨著原產(chǎn)地規(guī)則比例要求的變化,企業(yè)的利潤和實際達成原產(chǎn)比例變換呈現(xiàn)相反的趨勢。具體來說,當原產(chǎn)比例要求低于35%時,企業(yè)決策基本保持不變,此時產(chǎn)成品的實際原產(chǎn)比例可以達到35%。由于原產(chǎn)比例要求不高,企業(yè)可以相對自由配置供應鏈網(wǎng)絡(luò),因此利潤也維持較高的水準。此時的利潤基本與場景3中的結(jié)果一致,由此也體現(xiàn)了區(qū)域累積規(guī)則能夠給相關(guān)企業(yè)創(chuàng)造的價值,但是,當原產(chǎn)比例要求高于35%之后,受限于這一要求,企業(yè)的供應鏈布局不斷發(fā)生變化。由此,產(chǎn)成品的實際達成原產(chǎn)比例也相應提升,但利潤在不斷下降。
綜合以上結(jié)果可知,原產(chǎn)地規(guī)則會顯著影響決策者的供應鏈布局。在非區(qū)域累積規(guī)則下,具有產(chǎn)業(yè)集聚優(yōu)勢的國家會受到跨境布局企業(yè)的偏好。而RCEP的區(qū)域累積規(guī)則下企業(yè)可以在域內(nèi)自由布局,減輕了關(guān)稅壁壘對于跨境供應鏈利益實現(xiàn)的干擾,有望給企業(yè)帶來更大的收益,但是,隨著企業(yè)的跨境布局,在RCEP實施后,企業(yè)將面臨著跨境運作和物流的挑戰(zhàn)。
3 結(jié)束語
海外布局的制造企業(yè)面臨原產(chǎn)地規(guī)則的制約和挑戰(zhàn)。本文針對紡織企業(yè),在考慮原產(chǎn)地規(guī)則以及RCEP協(xié)定的基礎(chǔ)上,研究了包括工廠選址、產(chǎn)能規(guī)劃、供應商選擇、原料采購、成品生產(chǎn),以及運輸?shù)仍趦?nèi)的供應鏈網(wǎng)絡(luò)設(shè)計決策。為此,構(gòu)建了相應的混合整數(shù)非線性規(guī)劃模型。為實現(xiàn)對模型的最優(yōu)求解,先將其線性化,然后設(shè)計了基于Benders分解的最優(yōu)求解算法。最后,通過將其應用于某企業(yè)的海外布局決策中,對于包含RCEP協(xié)定的3種情況進行了仿真對比,驗證了本文工作的有效性,也分析了原產(chǎn)地規(guī)則,特別是RCEP協(xié)定中區(qū)域累積規(guī)則所帶來的影響。
由于跨境貿(mào)易影響因素眾多,在后續(xù)的研究中,結(jié)合重要而緊迫的因素,如人民幣國際化、貿(mào)易摩擦等展開研究,是未來的一個可能的方向。在這些因素中,有相當一部分存在不確定性,由此,根據(jù)隨機因素特征的不同,選取合適的不確定優(yōu)化方法展開供應鏈網(wǎng)絡(luò)的優(yōu)化設(shè)計,這也是未來的主要研究內(nèi)容。

