基于BP-PSO的致密氣壓裂施工參數優化

郭大立， 唐乙芳， 李曙光， 張天翔， 康蕓瑋

(1.西南石油大學理學院, 成都 610500； 2.中聯煤層氣國家工程研究中心有限責任公司, 北京 100095；3.中石油煤層氣有限責任公司, 北京 100028)

中國致密氣資源豐富[1]，為了有效開發致密氣資源，需要對致密氣井進行增產改造，合理的壓裂設計對壓裂改造是至關重要的，開展致密氣壓裂施工參數優化方法的研究意義重大[2]。國內外學者對壓裂施工參數優化做了大量研究。整體上壓裂施工參數優化方法有3種：①基于數學模型或理論公式，采用離散元方法、變粒徑和變排量技術等方法對壓裂施工參數進行優化[3-4]；②軟件模擬技術，利用三維壓裂軟件FracproPT、Meryer軟件和有限元軟件ABAQUS等軟件對壓裂施工進行模擬[5-6]，從而優化壓裂施工參數；③機器學習，基于支持向量機、人工BP(back propagation)神經網絡、大數據人工智能計算等方法建立了壓裂施工參數優化模型[7-9]。姚鋒盛等[10]利用壓裂軟件FracproPT對壓裂施工液量、排量、加砂量等參數進行模擬分析，從而優化二次加砂壓裂施工參數；龔訓等[11]提出了針對不同區域特征的分帶壓裂法，并利用壓裂軟件PT對不同區塊的壓裂施工參數進行優化，從而得到不同區域的壓裂施工參數。李鐵軍等[12]利用隨機森林與交叉驗證相結合的方法篩選出影響日產氣量的地質工程主控因素，提出了熵值法的逼近理想排序法的綜合評價方法的工程主控因素的最優區間確定方法；李凌川等[13]通過巖心實驗和理論計算分析儲層和天然裂縫等相關特征，應用數值模擬技術優化了壓裂施工參數。

由于現場常用的壓裂施工參數設計方案，基本上是根據儲層的物性、巖性、巖石力學性質等影響參數，通過現場已有的壓裂軟件和數值模擬技術，從而計算得到壓裂施工參數，但這些方法缺乏對其他致密氣井儲層施工經驗的學習和借鑒，及只對壓裂施工參數優化出了最優區間，沒有優化出精準的施工參數值，結果不夠精準[14-15]。而有些學者利用機器學習方法建立施工參數優化模型時，并沒有討論參數個數和模型參數配置對模型的影響，導致所優化得到的最優壓裂施工參數不夠精準[16-17]。因此，在現場壓裂設計中對施工參數精準設計成為壓裂施工的關鍵問題。

為了解決壓裂施工方案精準設計的問題，合理設計壓裂施工參數，達到致密氣井增產的目的。在大數據和機器學習的驅動下，充分運用了大數據的特點。為了提高模型的泛化能力，討論了模型的參數設置。現基于X區塊97口井的測井數據，首先利用灰色關聯分析篩選主控因素。再次討論致密氣井影響參數個數對BP神經網絡模型的影響，并引入交叉驗證對樣本量不足時對模型的處理。最后基于反演思想，建立粒子群算法(particle swarm optimization，PSO)日產氣量最優化模型，從而反算出最優壓裂施工參數。為現場壓裂施工方案精準設計提供一種新的方法。

1 模型建立及求解

在大數據和機器學習背景下，以數據為導向建立了致密氣井壓裂參數優化反演模型。建立反演模型過程中主要涉及的理論基礎有灰色關聯度分析、BP神經網絡及粒子群算法。

1.1 數據預處理

在多元統計分析學中，應用于數據降維處理的方法主要有主成分分析、因子分析和灰色關聯度分析等方法，這些方法都是多因素統計分析法。從數學意義上看，這些方法都是降維處理技術。基于數據的特征，主要使用灰色關聯分析方法，該方法通過計算出的灰色關聯度值來描述比較數列與參考數列之間的關系強弱，將得到的關聯度值進行排序，從而達到對數據降維處理的目的。使得消除冗余的信息，更全面地提取出數據集的信息。高維數據作為BP神經網絡的輸入參數，將增加模型空間和時間復雜度，不利于模型的訓練。由于各因素與平均日產氣量間存在復雜的非線性，不能簡單地通過一元線性模型判斷兩者之間的關聯性。需通過計算各因素與平均日產氣量間的關聯度，并將各因素的關聯度進行排序。

由于原始數據存在缺失、量綱、異常等問題，所以對數據進行灰色關聯度分析時，需對原始數據進行預處理[18]。預測模型會受到數據量綱的影響，使得預測模型的預測結果不準確，即需要對數據進行歸一化處理，歸一化處理方法主要有平均數方差法和極差歸一化法[19]，本文中采用極差歸一化。用于歸一化處理的樣本有97個，每個樣本共有16個自變量，1個因變量，構成一個97×17階的數據矩陣。

1.1.1 極差歸一化

設p維向量X=(X1,X2,…,Xp)的原始矩陣為

(1)

式(1)中：n為樣本數，n=97；p為每個樣本變量數，p=17。

將原始矩陣X進行極差歸一化后的矩陣為

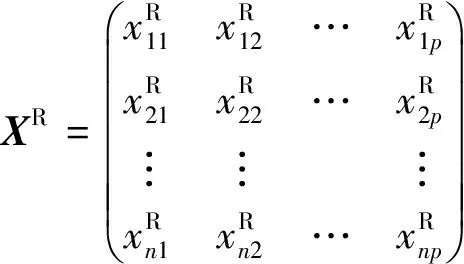
(2)

i=1,2,…,n；j=1,2,…,p

(3)

1.1.2 計算灰色關聯度

依次計算出16個參數的比較數列與參考數列(平均日產氣量)間的絕對差值。

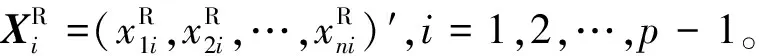
(4)

式(4)中：ρ為分辨系數，取值范圍為(0,1)。若ρ越小，關聯系數間差異越小，區分能力就越弱，一般ρ取0.5。

關聯度為

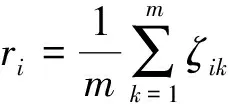
(5)

1.2 基于粒子群算法的反演模型

在粒子群算法優化中，需建立自變量與因變量之間的映射關系為目標函數。本文中由于各因素與平均日產氣量間存在高度復雜的非線性關系，用單一的多元線性關系并不能準確表示它們之間的關系，所以需建立BP神經網絡[20]模型作為粒子群算法的目標函數。如圖1所示，BP神經網絡是解決不確定的控制系統、數據間存在高度復雜的非線性的一種方法，并且是一種分布式多線程并行處理信息的數學方法。BP神經網絡主要由輸入層、隱含層和輸出層構成。位于輸入層和輸出層之間的是隱含層，它像是一個黑盒，是沒有與外界數據有直接接觸的一個神經元，對輸入、輸出間關系有較大影響，確定隱含層結點數對模型有無泛化能力至關重要。通過灰色關聯度排序，只能確定各因素與平均日產氣量間的強弱，并不能確定參數個數對BP神經網絡模型擬合和預測誤差的影響，即討論參數個數對模型的影響是非常有必要的。BP神經網絡模型訓練過程中涉及多個參數，而參數的設置缺乏理論指導。精準的參數設置會使得模型的泛化能力更好，即討論參數的設置對模型來說是至關重要的。

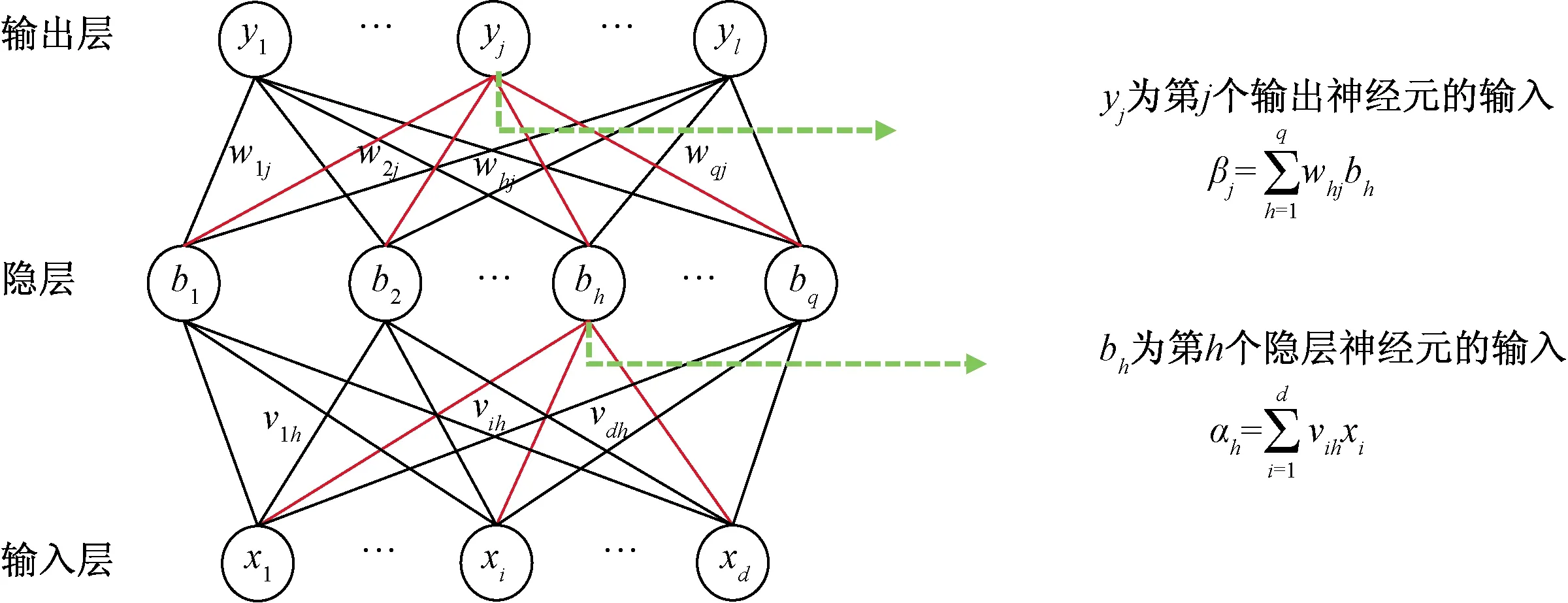
圖1 BP神經網絡結構Fig.1 BP neural network structure

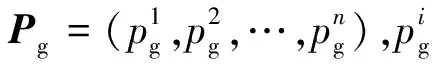
當最優解為局部極大值時，可通過調節能力常量ω大小跳出局部解，從而找到全局最優解。第i個粒子的速度更新公式為

(6)

式(6)中：ω為能力常量，控制前一時刻速度對當前時刻速度的影響，為非負數；c1為調節粒子朝著自身最優方向的步長；c2為調節粒子朝著全局最優方向的步長；r1、r2為相互獨立的偽隨機數，服從[0,1]上的均勻分布。

第i個粒子的位置更新公式為

xi(t+1)=vi(t)+vi(t+1)

(7)

將每一個xi代入目標函數中算出一個適應值，將t+1時刻適應值與t時刻最優值進行比較。如果t+1時刻適應值大于t時刻最優值，則最優位置進行更新，否則不進行更新。

粒子i的當前最優位置為

(8)

最終搜索到每個粒子的全局最優解，從而反演出壓裂施工參數最優值。

2 實例分析

2.1 數據采集及分析

X區塊位于鄂爾多斯盆地，基本構造格局為“一隆一凹兩斜坡”，即一隆指的是中部的桃園背斜帶，一凹指的是蒲縣凹陷帶，兩斜坡主要指的是西部斜坡帶和東部明珠斜坡帶。收集、整理及初步分析了位于X區塊致密氣2013—2018年地質、壓裂、排采等資料230 G，樣本量達到170井次以上，其中只有97口井的測井數據是完整的，即樣本量為97口井。

如圖2～圖4所示，平均日產量都是隨著液量、施工排量和支撐劑量的增大而增大，對于產量而言施工排量和加砂量越大越好(大排量、大砂量)，更容易形成復雜縫網，從而增加日產量，但壓裂施工參數存在最優區間。根據壓裂施工數據分析，針對不同的壓裂液，壓裂施工參數設計量是不同的。當壓裂液是滑溜水時，液量設計為1 000～1 500 m3，支撐劑量設計為70～100 m3，施工排量設計為8～15 m3/min；壓裂液是胍膠時，液量設計為100～500 m3，支撐劑量設計為20～40 m3，施工排量設計為2～6 m3/min，此時壓裂施工效果較好，為后續壓裂施工參數的精準設計提供了最優優化區間。

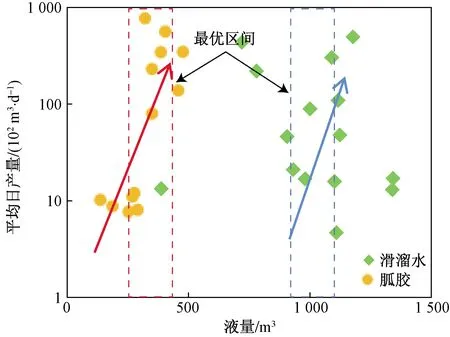
圖2 液量與平均日產量圖Fig.2 Diagram of liquid volume and average daily output

圖3 支撐劑量與平均日產量圖Fig.3 Support dose and average daily production diagram

2.2 影響致密氣井產氣量的參數初選與優選

致密氣井壓裂效果主要受致密氣層地質因素和壓裂施工參數的影響。初選出測井(電阻率、密度、聲波時差、孔隙度、含氣飽和度、層厚、自然伽馬)、巖石力學(靜態楊氏模量、泊松比、最小水平主應力、上隔層應力差、下隔層應力差)和壓裂施工(液量、支撐劑量、平均砂比、施工排量、前置液百分比)共17個參數。其中測井和巖石力學參數是不可控參數，而壓裂施工參數是可控參數。通過灰色關聯度分析只知道各參數間的排序結果，如圖5所示，從中優選出幾個參數是不確定的，需考慮參數個數對BP神經網絡模型擬合和預測精度的影響，由此來確定優選影響參數的個數。

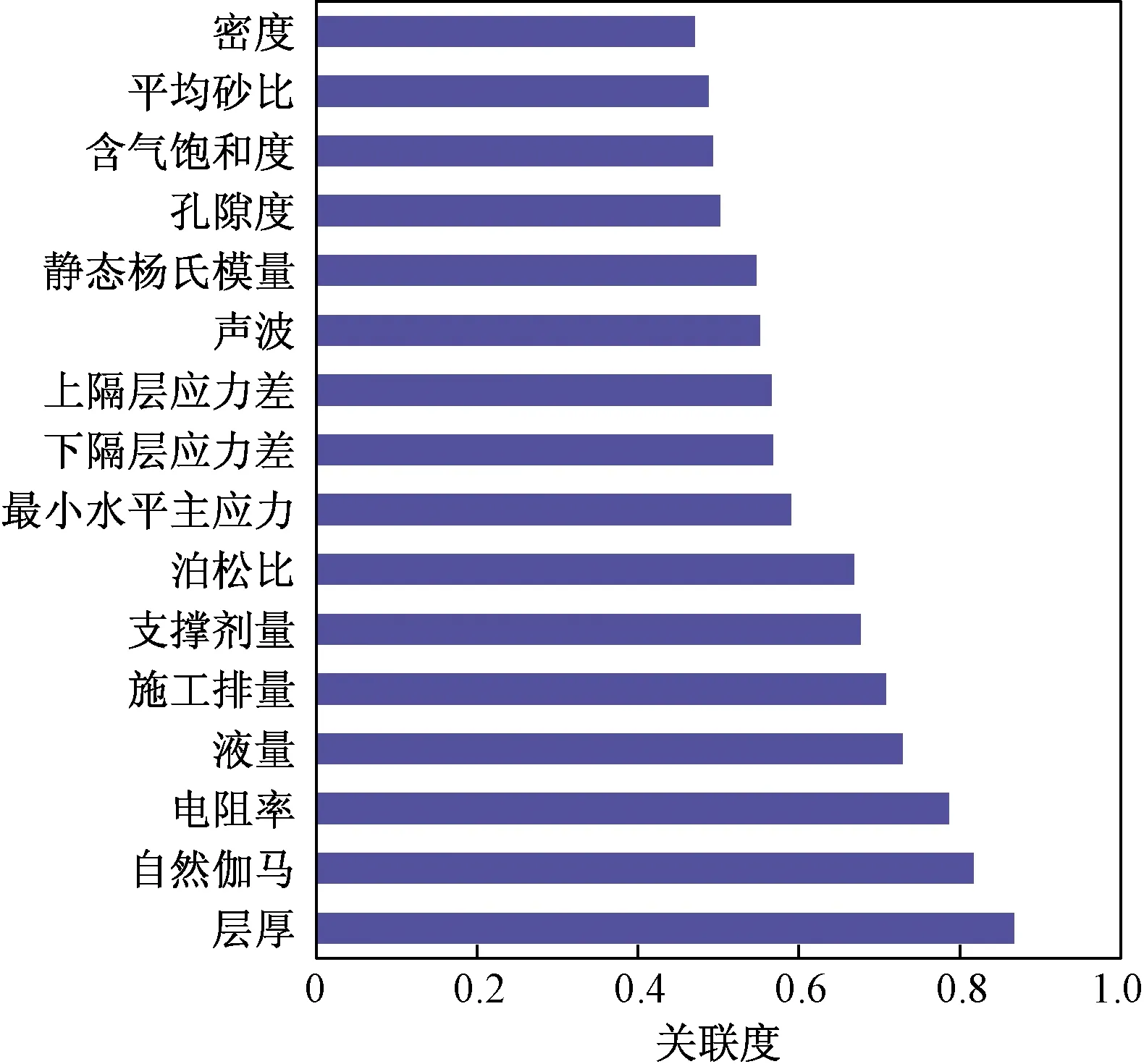
圖5 灰色關聯度分析結果Fig.5 Grey relational analysis result

2.3 建立BP神經網絡模型

在利用機器學習進行模型訓練時，為保證訓練模型的泛化能力，往往是需要一定的訓練樣本量。如果訓練樣本量過少將會導致模型泛化能力弱。本文中由于樣本量不充足，為了充分利用數據集對模型效果進行測試。在搭建預測模型時，需要將數據集分為訓練集和測試集兩個數據集，訓練集的目的就是搭建模型和測試模型的擬合精度，而測試集的目的就是測試模型的預測精度。本文中為了提高模型的擬合和預測精度，在對模型進行訓練時，將數據集隨機分為k個包，測試集是隨機選取其中一個包，訓練集是剩余k-1個包，并將訓練集進行訓練。

由于樣本量不足，為了充分利用數據，在訓練模型時使用10重交叉驗證。即將數據集隨機分成10個包，每次訓練時，測試集是從10個包中隨機選取一個包，訓練集是剩余的9個包，這樣組成一組數據集。反復進行10次，組成10組數據集，將每組的數據集代入BP神經網絡進行訓練，如圖6所示，求每組數據集中測試數據的誤差平均值就是該模型準確率。本文中總樣本有97口井，將90口井隨機分成9個包，每個包中有10口井，剩余的7口井組成一個包，總共將數據分為了10個包，該方法在樣本量低于50時就不適用。通過構建一個包含1層隱含層的BP神經網絡，其隱含層結點數為9個節點。討論不可控參數個數對模型擬合和預測誤差的影響，如表1所示，參數個數對擬合和預測誤差的影響是無規律的。在綜合考慮擬合和預測誤差下，優選10個參數(不可控參數：層厚、電阻率、泊松比、最小水平主應力、隔層應力差、孔隙度；可控參數：液量、支撐劑量、平均砂比、施工排量、前置液百分比)，作為模型的輸入參數。本文搭建的模型中，輸入層到隱含層的神經元傳遞函數采用tansigmoid型函數，隱含層到輸出層的神經元傳遞函數選擇輸出任意取值的pureline型線性神經元。將訓練好的BP神經網絡模型進行保存，為后續壓裂施工參數優化做好鋪墊。

表1 參數個數對BP神經網絡模型擬合和預測精度影響結果

tansig函數為

(9)

式(9)中：n為變量。

BP神經網絡模型為

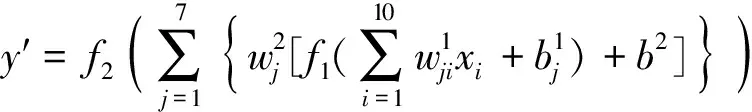
(10)

式(10)中：y′為輸出層計算結果；xi為輸入層樣本，即影響平均日產氣量各因素；i為輸入層節點數，i=1,2,…,10；j為隱含層節點數，

3 基于粒子群算法的壓裂參數優化反演模型

由于粒子群算法是一種簡單易實現的方法，同時具有收斂速度快、解質量高、魯棒性好等特征，因此從出現至今，被迅速應用到許多科學和工程領域。將BP神經網絡訓練好的模型，作為粒子群算法的目標函數。BP神經網絡模型的輸入參數中有可控參數和不可控參數，通過粒子群算法尋找目標函數(平均日產氣量)的最大值，從而反演出可控參數的值，即壓裂施工參數(液量、支撐劑量、平均砂比、施工排量)。

圖6 BP神經網絡訓練流程Fig.6 BP neural network training process

基于海量的壓裂施工數據，以大數據為導向建立粒子群算法的壓裂施工參數優化新方法。通過建立的BP神經網絡模型為目標函數，目標函數中共有10個變量，其中不可控變量有6個，可控變量有4個。在進行以平均日產氣量為目標函數優化過程中，每個樣本的不可控變量值不變，通過優化目標函數最大值，從而反演出可控變量的值。目標函數的約束條件為4個可控變量的最優區間，及平均日產量與可控變量的多元線性回歸函數，其R2=0.987 5。通過調節粒子群算法中的參數，確定最優目標值下的c1和c2參數的值，確定c1=1.494 4和c2=1.237 6，及進化次數max gen=200和種群規模sizepop=300。

目標函數(最大值)為

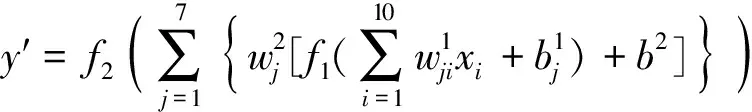
(11)

式(11)中：xi(i=1,2,…,6)是不可控變量，為固定值；xi(i=7,8,9,10)是可控變量，為目標函數的自變量。

約束條件為

(12)

以產量和經濟效益為目標，系統精準優化壓裂設計方案及施工參數(施工排量、用液量、加砂量等)提出優化的液體方案、支撐劑方案。應用于X區塊的97口致密氣井，BP神經網絡模型準確率為86.52%。對7口井進行壓裂施工參數優化后，每口井所有層的總平均增產率為5.57%。其中7口井的具體壓裂施工參數優化方案，如表2所示，優化前后壓裂施工參數對比圖，如圖7～圖10所示。優化的7口井，如表3所示，每口井所有層的平均總增產率為5.57%，每口井所有層的平均日增產量為50 m3以上。現場可以根據計算出的壓裂施工參數值合理地配制壓裂液，不造成壓裂液的浪費，從而節約了壓裂施工成本。在進行壓裂施工方案設計時，可以參考多種方法的結果，使得壓裂施工方案設計的更加合理。該方法從過去現場壓裂施工數據出發，充分地結合了機器學習。該方法與現有方法相比，投入的經濟成本低和操作方便，產生的回報高等優點。表明該方法對現場壓裂施工設計具有一定的指導作用，提高了整個X區塊的經濟效益。

表2 7口井壓裂施工參數優化結果

圖7 液量優化前后對比圖Fig.7 Comparison chart before and after liquid volume optimization

圖8 支撐劑量優化前后對比圖Fig.8 Comparison chart before and after support dose optimization

圖9 平均砂比優化前后對比圖Fig.9 Comparison chart of average sand ratio before and after

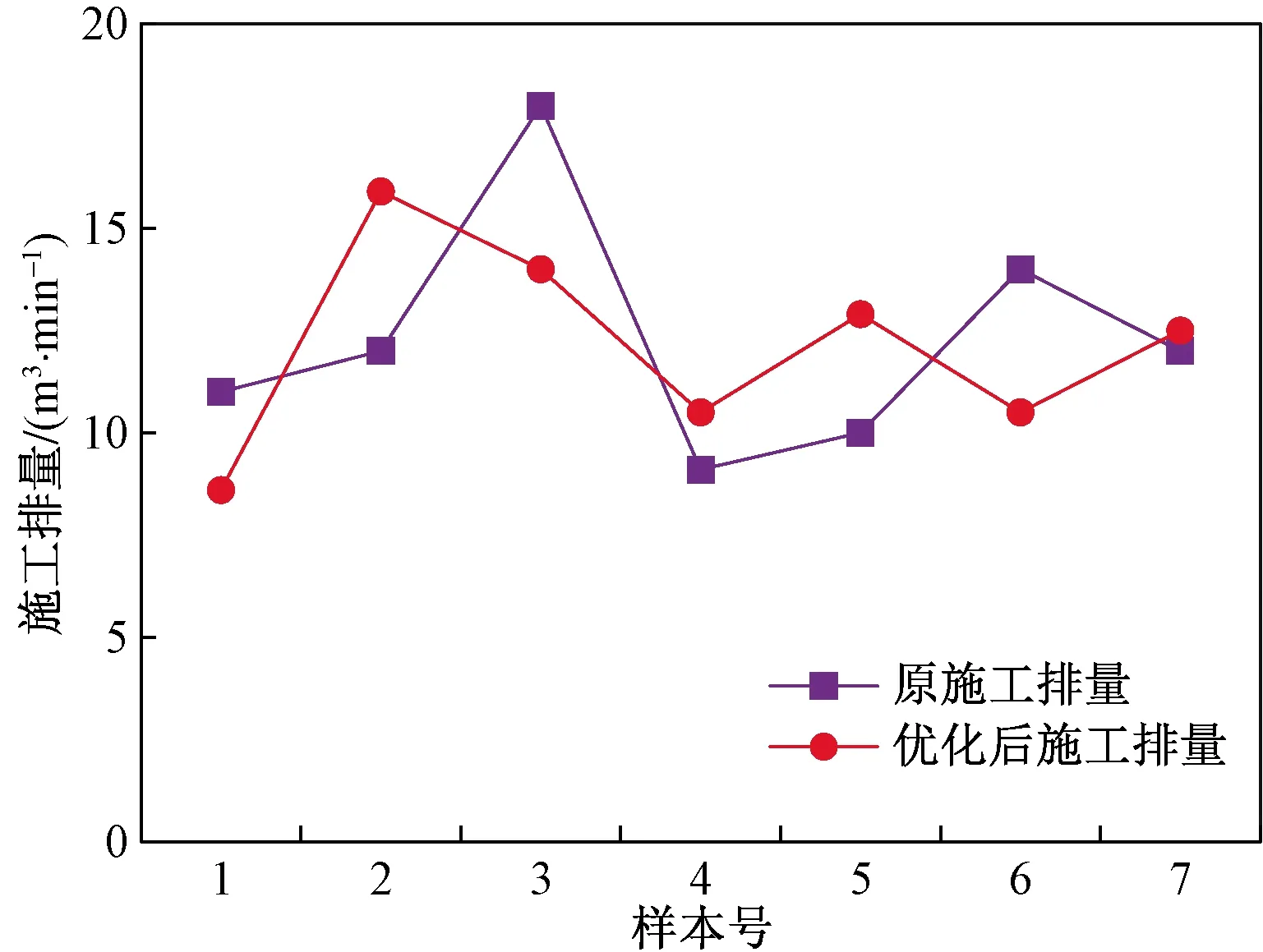
圖10 施工排量優化前后對比圖Fig.10 Comparison chart before and after operation displacement optimization

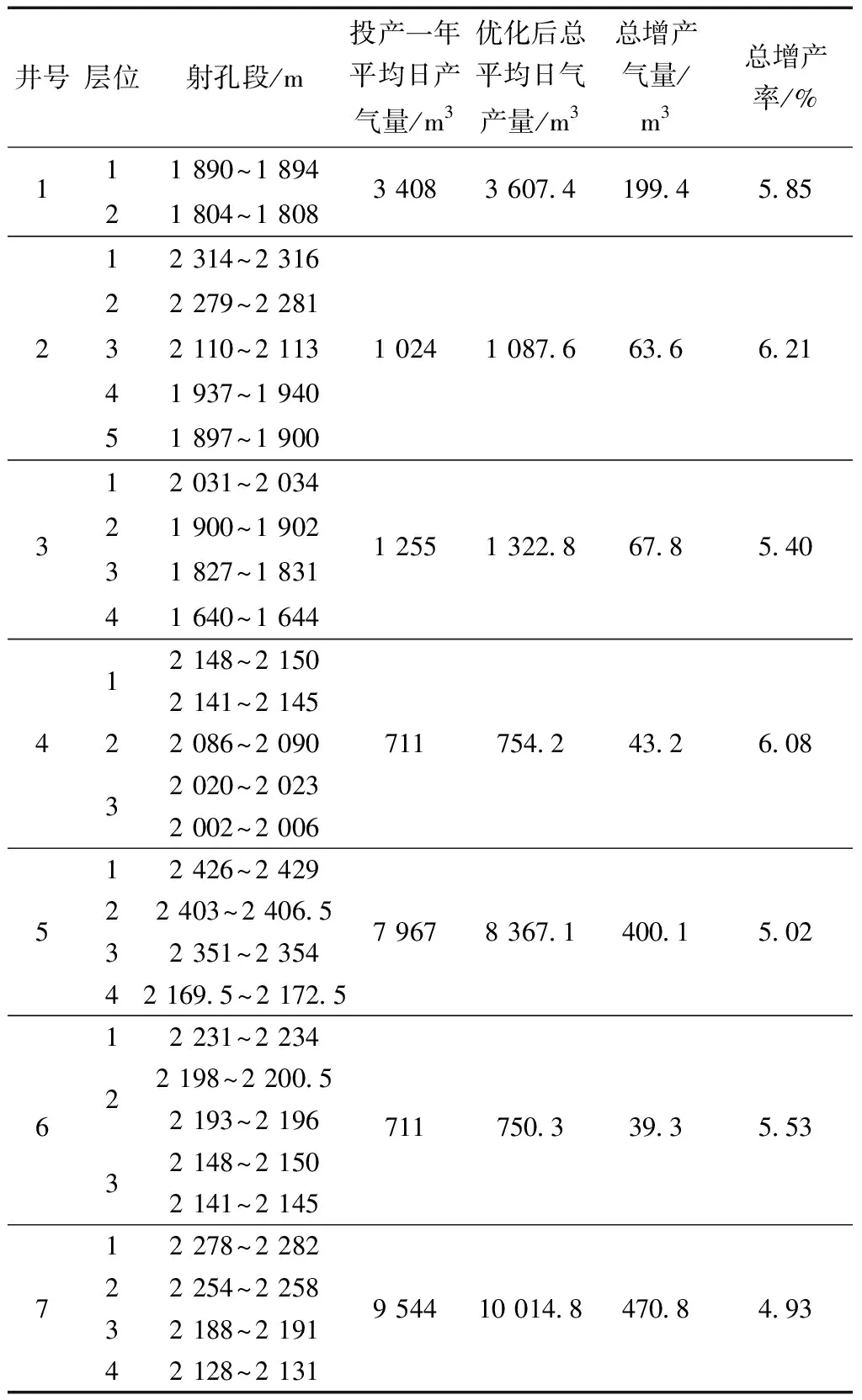
表3 7口井所有層的總增產氣量

4 結論

(1)在進行BP神經網絡模型訓練時，為了充分利用樣本數據集，使用10重交叉驗證，最終構建了一個含有9個節點的隱含層的10重交叉驗證-BP神經網絡模型。

(2)輸入參數個數將影響BP神經網絡模型的擬合和預測精度，恰當的輸入參數個數將提高模型的精度。討論了不同參數個數對BP神經網絡模型擬合和預測精度的影響，最終確定了10個輸入參數(6個不可控參數：層厚、電阻率、泊松比、最小水平主應力、隔層應力差、孔隙度；4個可控參數：液量、支撐劑量、平均砂比、施工排量)。以及討論了模型參數對模型精度的影響。

(3)應用于X區塊的97口致密氣井，BP神經網絡模型準確率為86.52%。對7口井進行壓裂施工參數優化后，每口井所有層的總平均增產率為5.57%。