一種優化組合模型及其在高鐵路基凍脹 變形預測的應用

魏冠軍, 梁斌, 戴嵩, 張幸, 王瀚弘

(1.蘭州交通大學測繪與地理信息學院, 蘭州 730070； 2.地理國情監測技術應用國家地方聯合工程研究中心, 蘭州 730070； 3.甘肅省地理國情監測工程實驗室, 蘭州 730070)

高鐵路基的穩定性與變形控制是高鐵施工、運營過程的關鍵,凍土地區高鐵路基的不均勻凍脹將會影響路基穩定性與軌面平整度,給高鐵行車安全帶來嚴重危害。將高鐵路基凍脹變形看作變化復雜的時間序列變化工程,在這個變化過程中包含眾多不確定性與復雜性以及外在影響因素。由于高鐵路基凍脹變形的復雜性導致單一模型對高鐵路基凍脹變形進行分析、預測時由于參數獲取的誤差以及模型自身局限性,使得預測結果不是很理想。

近年來,灰色理論、回歸分析、最優化理論以及神經網絡等數學分析方法廣泛應用于高鐵路基變形分析、預測。陳洋等[1]通過灰色穩健總體最小二乘估計對高鐵變形進行預測,先提出部分變量誤差模型的總體最小二乘估計并在此基礎上提出基于系統抗差估計方法(institute of geodesy & geophy-sics,IGGⅢ)抗差方案部分變量的總體最小二乘穩健估計,解決了預測過程中觀測值粗差定位與提出的問題。劉海鵬等[2]對路基變形規律與影響因素進行分析并構建了預測模型,在研究了振次、路基深度和含水率對路基變形的影響基礎上提出了累計塑性變形預測模型。張獻州等[3]在灰色模型的基礎上通過傅里葉級數與馬爾科夫模型對預測值進行修正,通過對預測殘差的分解與馬爾科夫修正計算提高預測精度的準確度。丁恒等[4]通過將變形周期項與趨勢項相結合得到位移預測函數更好的預測位移變化。康昊華等[5]提出了一種適用于高鐵變形預測的組合模型,該模型通過小波去噪消除高鐵變形過程中隨機擾動影響的基礎上進行灰色模型預測,并對預測結果進行馬爾科夫殘差修正實現預測殘差的收斂與預測精度。李照眾等[6]基于貝葉斯參數優化的經驗模型預測收斂變形的趨勢項,然后采用支持向量回歸算法修正經驗模型的預測結果,在此基礎上構建高鐵變形預測組合模型。以上學者不僅對不同單一模型進行優化改進,并在此基礎上進行誤差修正建立組合模型提高預測精度,然而未能考慮到變形觀測測數據的非等間距特性并且由于單一模型自身本身局限性導致預測結果穩定性受到影響。

針對觀測數據非等間距特性與單一模型預測由于自身局限性導致預測效果效果不佳的問題,在建立非等間距灰色模型與非等間距回歸模型的基礎上,通過馬爾科夫模型對兩種模型擬合、預測結果進行殘差修正,以此來提高預測的準確度。在此基礎上,應用線性定權方法確定最優權值系數對兩種修正后模型進行有效組合。通過組合模型對高鐵路基進行凍脹變形預測,彌補了單一預測模型的局限性以及不穩定性,具有更有效的預測穩定性與更高的預測精度。

1 預測模型簡介

1.1 基于冪函數的非等間距灰色模型

通過變形序列x0=(x0(1),x0(2),…，x0(n))建立灰色模型[7-8],首先利用冪函數(x-0.5)處理變形序列后進行一次累加處理得到累加數列為

x1=(x1(1),x2(2),…，x1(n))

(1)

由式(1)序列建立微分方程

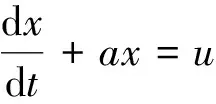
(2)

式(2)中：a為發展系數；u為灰色作用量。

由最小二乘原理利用凍脹變形觀測數據對參數a、u求解,將求解后參數代入微分方程并對微分 方程求解，公式為

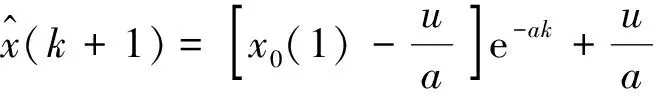
(3)

對求解序列進行累減、冪函數還原處理得到擬合、預測序列。k≤n-1時,求解值為已監測凍脹變形數據序列的擬合值；k>n-1時,求解值為未來時刻凍脹變形預測值。

擬合預測序列與原始序列求差計算殘差序列，公式為

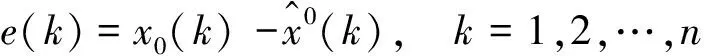
(4)

在灰色模型預測過程中,變形監測序列由于監測時距差異導致在模型中具有不同的貢獻程度。為解決監測時距差異對模型預測精度的影響,設置非等間距加權矩陣進行模型改進。定義時距遞增常數R與增長速度t(k), 規定t(1)=1,t(2)=2,R=1.5,增長速度與加權矩陣C為

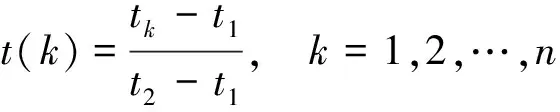
(5)

(6)

非等間距灰色模型參數矩陣求解修改為

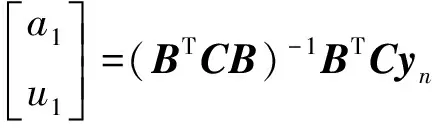
(7)

式(7)中：

1.2 非等間距回歸模型

采用單變量線性回歸預測模型對凍脹監測數據進行擬合預測,首先對路基凍脹變形觀測數據進行趨勢分析,依據數據變形趨勢選取線性回歸模型為

Yt=β0+β1x1+β2x2+…+βnxn

(8)

式(8)中：y為預測值因變量；x為觀測值自變量；β為系數矩陣。

向量表達形式為Y=Xβ。展開為

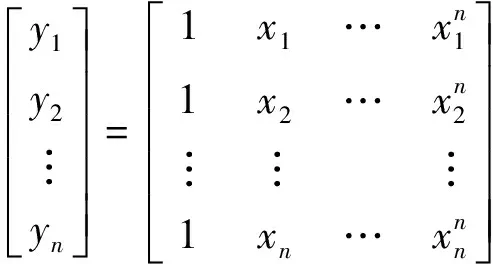
(9)

根據最小二乘原理計算通過路基凍脹變形觀測數據求解系數向量，即

β=(XTX)-1XTY

(10)

依據系數向量確定回歸模型狀態,利用回歸模型對凍脹變形數據進行擬合、預測。

擬合預測結果與原始數據求差計算得到殘差序列為

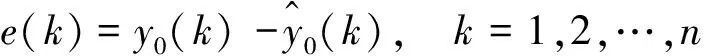
(11)

在參考灰色非等間距加權矩陣設置的基礎上,提出一種非等間距回歸模型。

非等間距回歸模型系數向量求解修改為

β=(XTCX)-1XT

(12)

式(12)中：C為非等間距加權矩陣；X為觀測值矩陣。

1.3 馬爾科夫預測基本原理

馬爾科夫過程是一種只需知道當前情況便可以確定將來狀態的隨機過程,通過狀態之間的轉移概率計算下一刻概率區間更新修正預測值[7-9]。通過馬爾科夫模型對灰色預測與回歸預測結果進行修正提高預測精度。基本建模過程如下：

根據模型擬合值與凍脹監測數據之間比值劃分狀態區間為

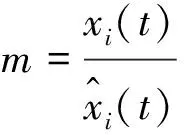
(13)

MI=[mi1,mi2]

(14)

計算狀態轉移概率,假設k時刻狀態i一步轉移到j次數為mij(k)，狀態i出現總次數為mi(k)，則狀態轉移概率為

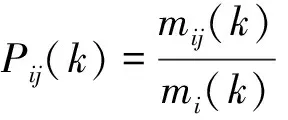
(15)

由狀態轉移概率構成狀態轉移矩陣為

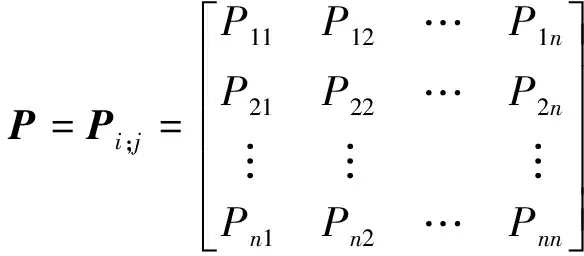
(16)

選取離目標最近的s期預測數據,按照由近到遠順序所需轉移步數分別為1,2，…，s。在轉移步數對應的轉移矩陣中選取起始狀態對應行向量為各狀態出現的概率,并將各自概率求和選取出現概率最大的狀態即為預測值所對應狀態。

得到預測值狀態區間選取區間中位數作為預測時刻相對值,預測修正值為

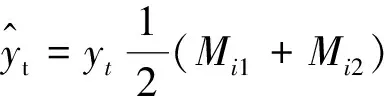
(17)

2 組合模型簡介

目前，針對高鐵路基凍脹變形的預測往往采用單一模型進行預測,每種模型都具有自身的優勢與不足[10-15]。由于凍脹變形的復雜性,采用單一預測模型可能存在片面性與不穩定性。在對非等間距灰色模型與非等間距回歸模型預測結果進行馬爾科夫殘差修正的基礎上,按照最優權重比例進行并聯組合,預測結果具有更好的精度與穩定性,組合模型預測流程，如圖1所示。

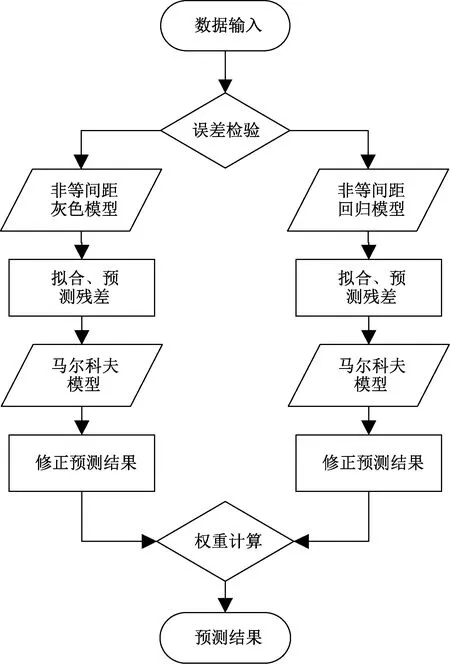
圖1 組合預測流程圖Fig.1 Combined prediction flow chart

2.1 最優權重確定方法

組合模型關鍵在于定權[16],定權方法主要有線性定權與非線性定權,其中線性定權是以誤差平方和最小為約束條件,對非等間距灰色模型與非等間距回歸模型擬合結果進行殘差修正后,兩種模型擬合結果準確度較高,因此選取線性定權方法。

組合模型權重通過模型擬合誤差按照極小化準測進行權重計算。

L個模型組合形式為

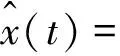
t=1,2，…，N

(18)

組合模型擬合誤差可以表示為

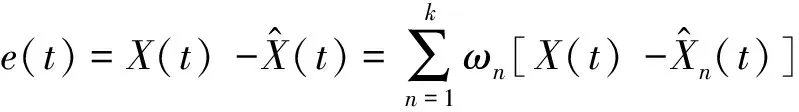
(19)

式(19)中：e(t)為殘差序列;ωn為權重系數。

Q=eTe=WTEW

(20)

RTW=1

(21)

式中:RT=(1,1,…,1);WT=(ω1,ω2,…,ωn);E=(eij),eij=eiTej。W為系數向量；E為誤差矩陣；R為單位向量。

若各個模型擬合誤差不相關,按照最小二乘法求解系數向量為

W=(RTE-1R)-1E-1R

(22)

2.2 精度分析

三種模型模擬預測結果分別采用三種精度評價指標[14-15]。

平均相對誤差：

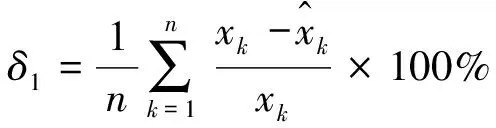
(23)

式(23)對模型模擬預測數據準確度進行評價。

誤差平方和：

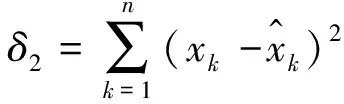
(24)

式(24)對模型擬合預測數據與原始觀測數據之間的離散程度進行評價。

平均絕對誤差：

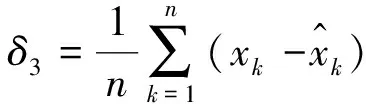
(25)

式(25)對模擬預測結果與真實值的偏離情況進行評價。

2.3 模型等級評價

本文預測結果采用后驗差方法檢驗,具體評價方法如下：

計算原始數列與殘差序列方差:

(26)

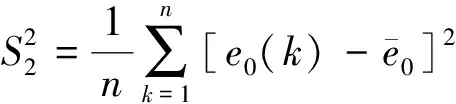
(27)

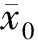
然后計算后驗差比值：

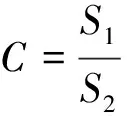
(28)

和小誤差概率：

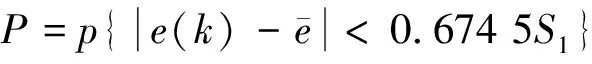
(29)

模型精度評價標準見表1。

表1 模型精度等級

3 工程實例分析

3.1 哈大高鐵路基凍脹監測數據預測

采用哈大線某區域路基表層凍脹期數據(表2)[14],該數據通過安裝在哈大線鲅魚圈K186+600處與K148+600處的非接觸式測量裝備對路基表層凍融數據進行監測,該數據精度可達0.01 mm,真實反映了該路段的路基凍融變化情況。

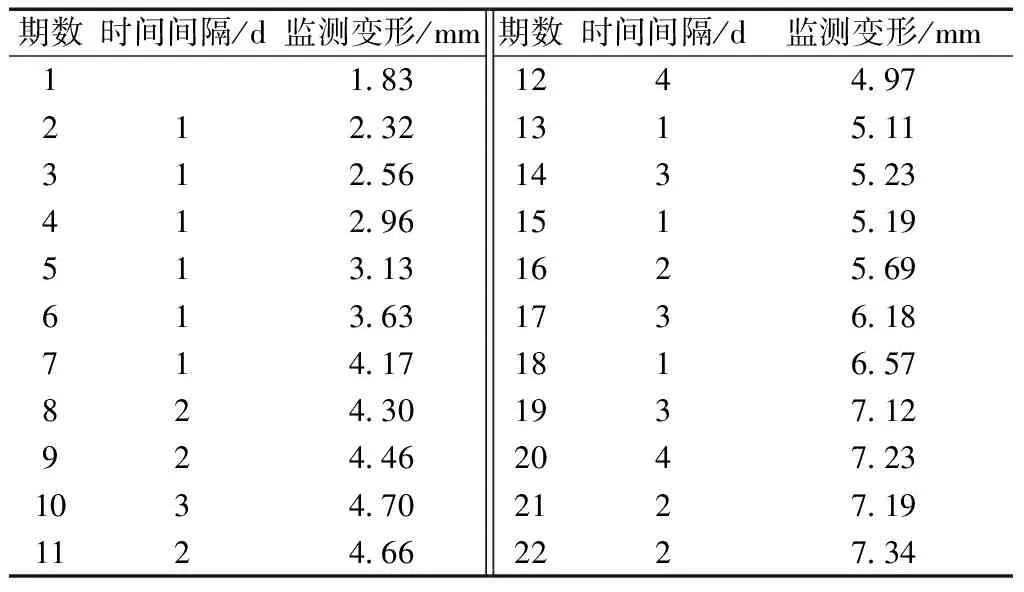
表2 算例1凍脹變形監測數據

3.1.1 非等間距灰色預測

計算非等間距灰色模型參數得到：a=0.026 5，u=0.619 9。由式(3)、式(4)計算得到非等間距灰色模型擬合值、預測值。

3.1.2 非等間距回歸預測

對已有數據進行趨勢分析后選用與本文數據擬合度最高的二次曲線,由式(7)～式(11)計算系數向量確定非等間距回歸模型為y=2.169+0.21x-0.001 7x2。由式(7)計算非等間距回歸模型擬合值與預測值。

3.1.3 馬爾可夫模型殘差修正

以灰色模型第20期馬爾可夫模型殘差修正過程為例簡要介紹馬爾可夫模型計算過程。

根據灰色預測模型的擬合結果,計算凍脹變形實際觀測值與模型擬合值的比值,根據比值的變化狀態劃分狀態區間為[0.89,0.96][0.97,1.01][1.02,1.08][1.09,1.22]。

根據狀態轉移概率公式[式(12)～式(15)]計算一步狀態概率轉移矩陣，即

由于狀態劃分為4個,選取離預測時刻最近的4期作為原始對象,其轉移步數分別為1、2、3、4,計算轉移概率見表3。

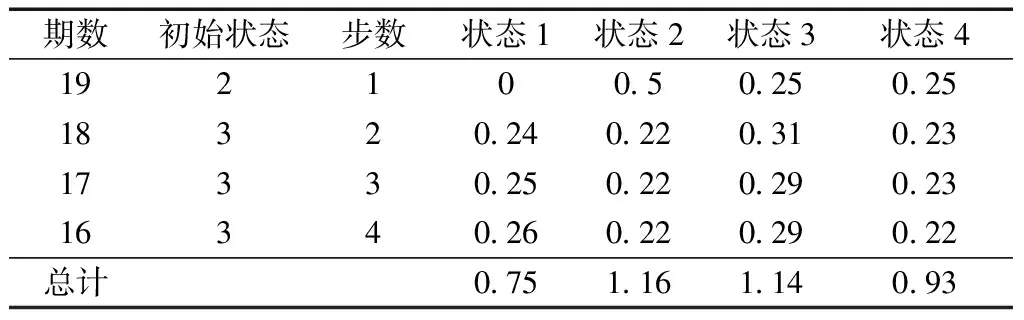
表3 算例1狀態預測

由表3可知,第20期預測值處于狀態區間2的概率最大,由式(17)計算得到該期預測修正值為7.135 mm。

3.1.4 權重系數計算與預測結果評價

由式(15)～式(18)計算灰色模型與回歸模型系數為ω1=0.711 5,ω2=0.288 5。

三種模型擬合、預測結果見表4、表5。

預測結果對比可得,本文組合模型的擬合、預測結果更具穩定性,預測結果更加接近于真實值。

3.1.5 模型等級、精度分析

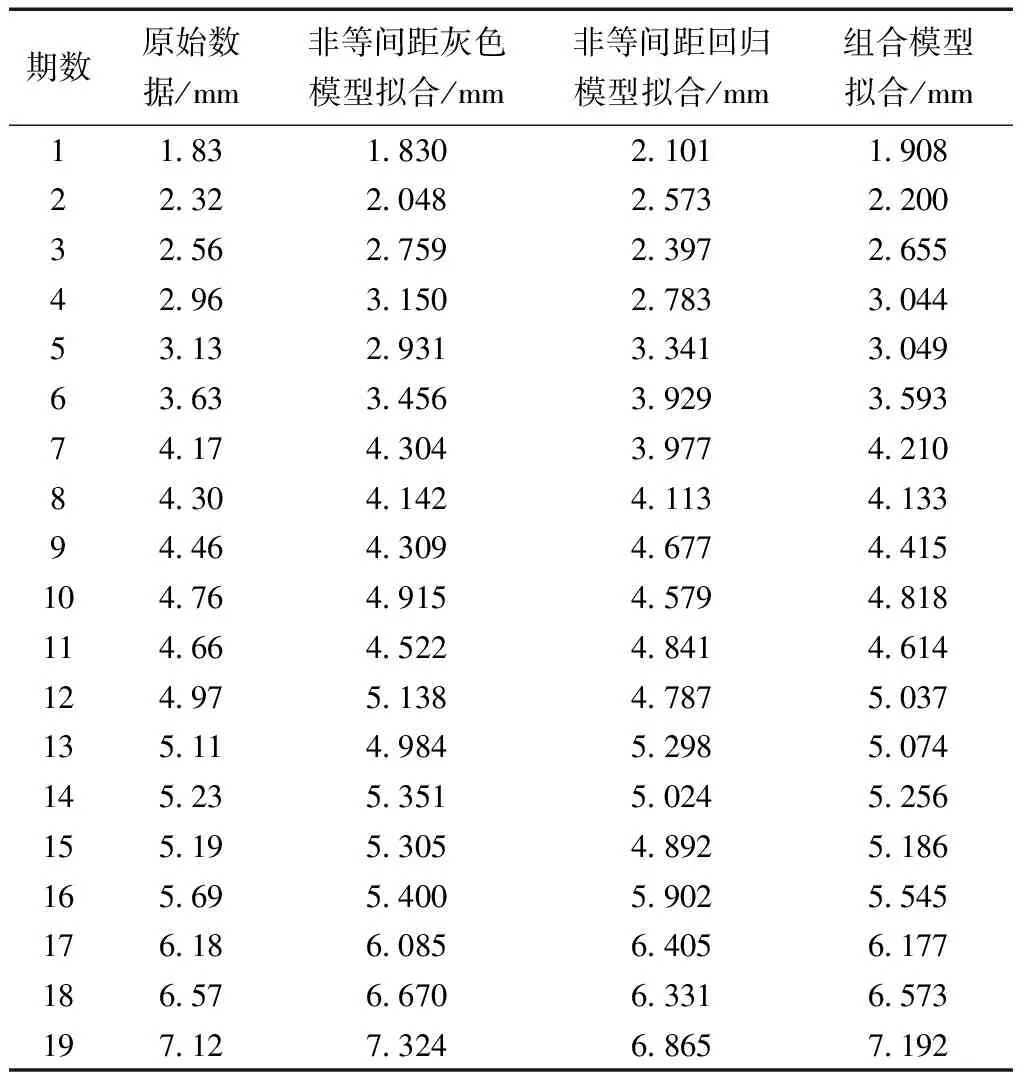
表4 算例1擬合結果對比

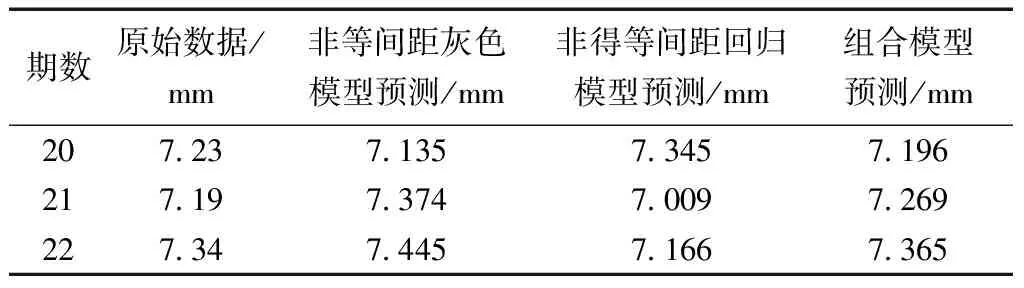
表5 算例1預測結果對比

由表1可得,組合模型預測精度等級滿足一級模型精度要求,組合模型可以較好地預測路基凍脹變形。

由式(22)～式(24)并結合表4、表5中數據計算2種模型誤差分析情況,如表6所示,三種模型對應的3項誤差單項數據變化情況如圖2～圖4所示。

由表6組合模型平均誤差指標小于非等間距灰色模型與非等間距回歸模型,圖2～圖4可以看出組合模型對于凍脹變形的預測表現優于單一模型。構建組合模型既 可以避免灰色模型對指數增長不明顯的數據預測效果不佳的問題,又可以改善回歸模型預測可靠性較弱的缺點。

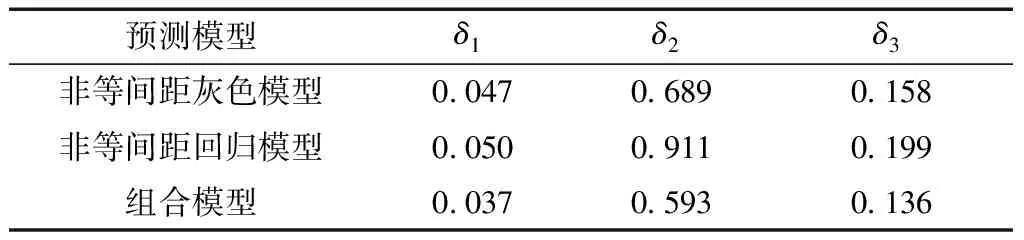
表6 算例1精度評價指標

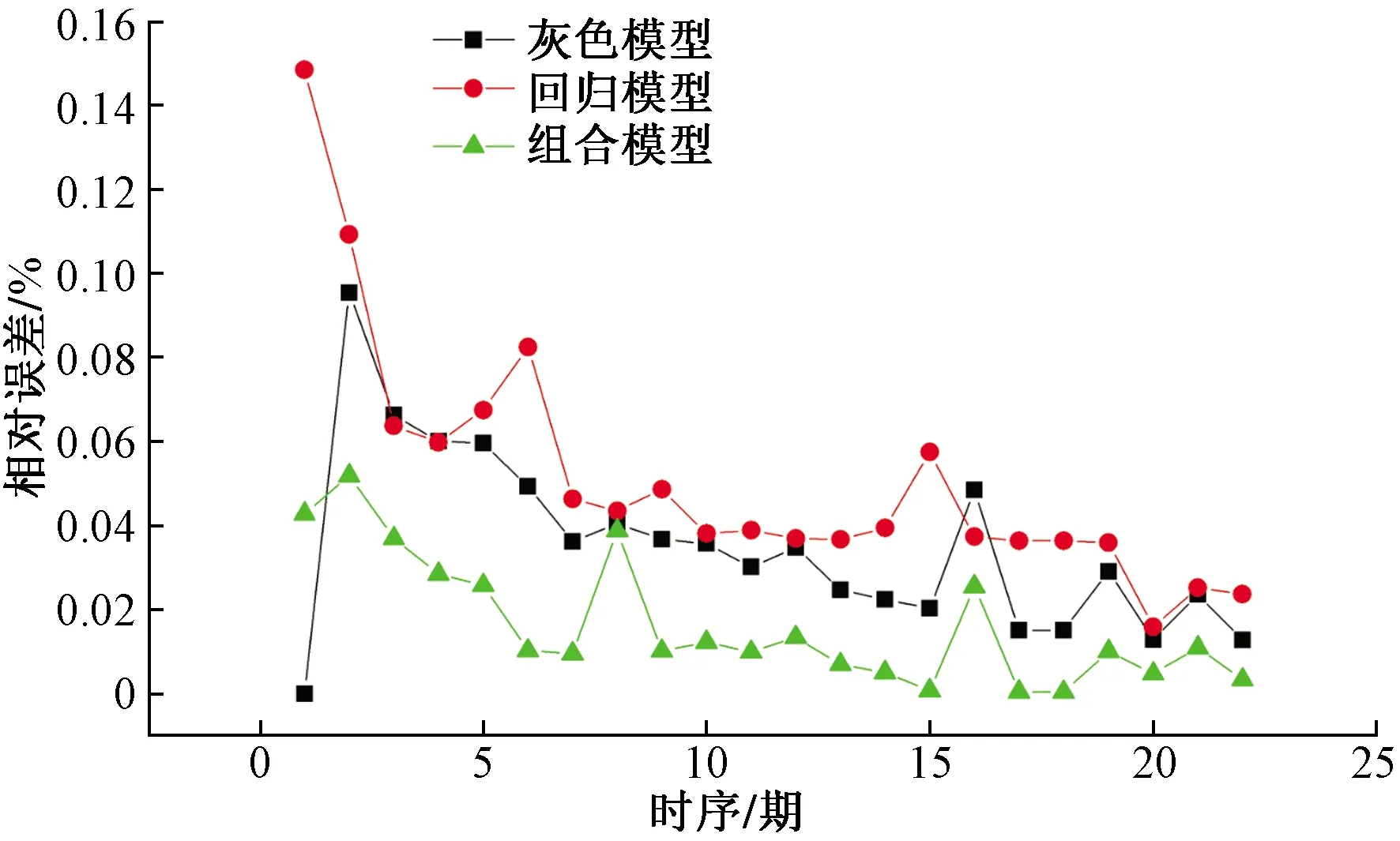
圖2 算例1相對誤差對比Fig.2 Relative error compare of example 1

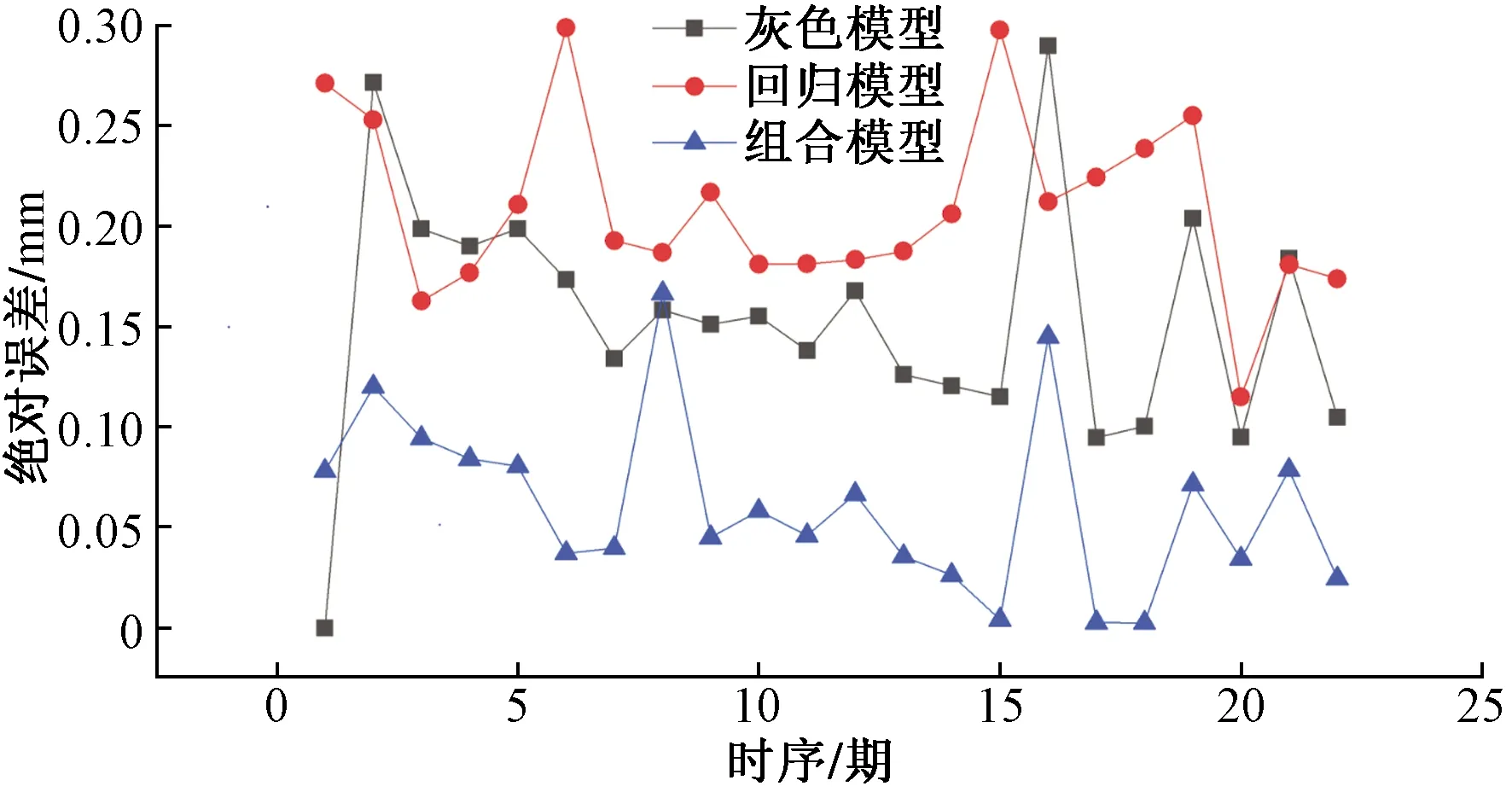
圖3 算例1絕對誤差對比Fig.3 Absolute error comparison of example1

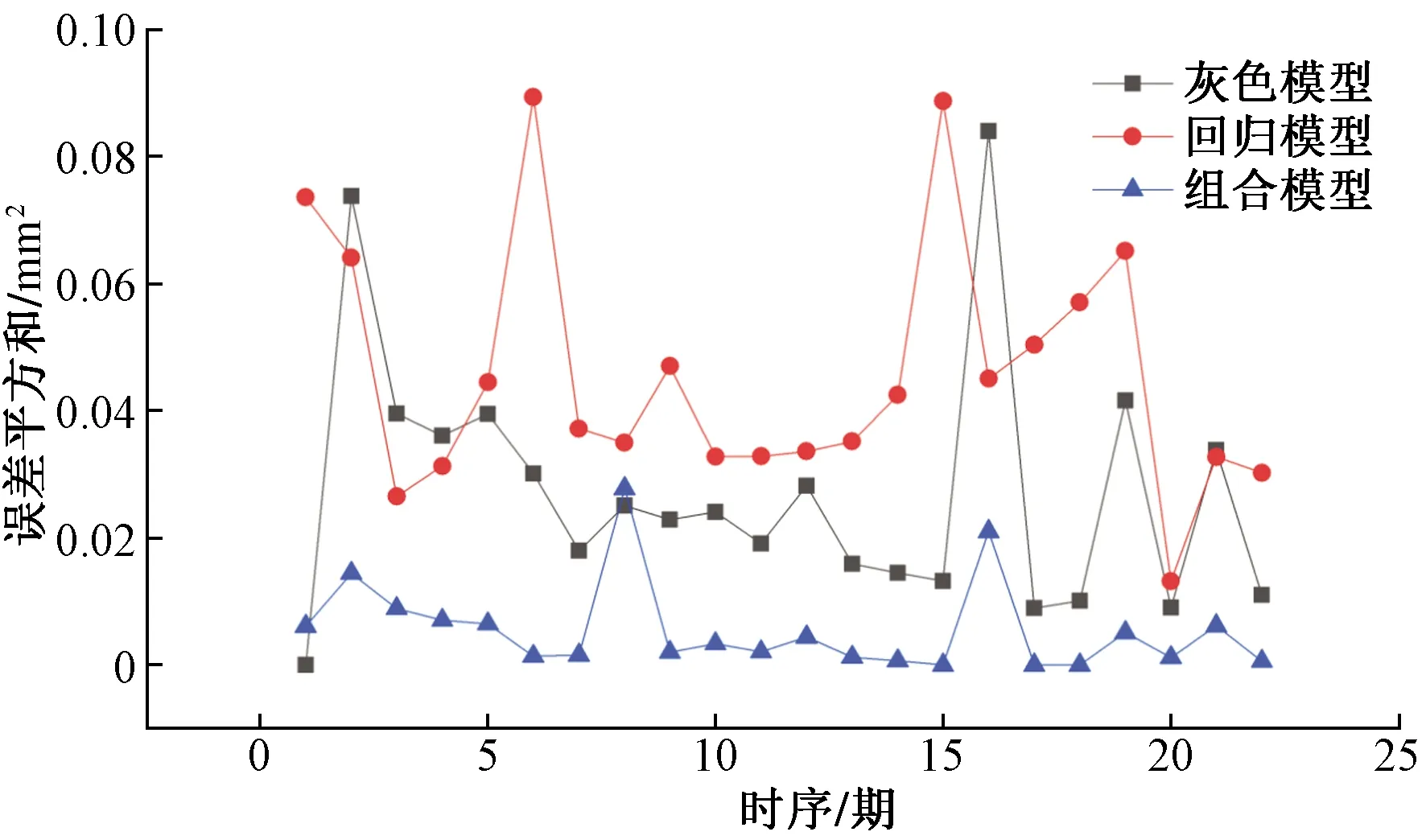
圖4 算例1誤差平方和對比Fig.4 Error sum of squares comparison of example 1

3.2 算例2-某寒區高鐵路基變形數據預測

以某寒區高鐵建設工程施工過程為例,選取項目內高速鐵路路基52號監測點的24期變形監測數據進行預測(表7)。

3.2.1 非等間距灰色預測

計算非等間距灰色模型參數得到a=0.003 7，u=1.244 1，由式(3)、式(4)計算得到模型擬合值、預測值。

3.2.2 非等間距回歸預測

對已有變形數據進行變形趨勢分析,選用與本文數據變形趨勢擬合度最高的二次曲線,由式(7)～式(11)計算系數向量確定非等間距回歸模型：y=0.622 5+0.416 0x-0.002 5x2。

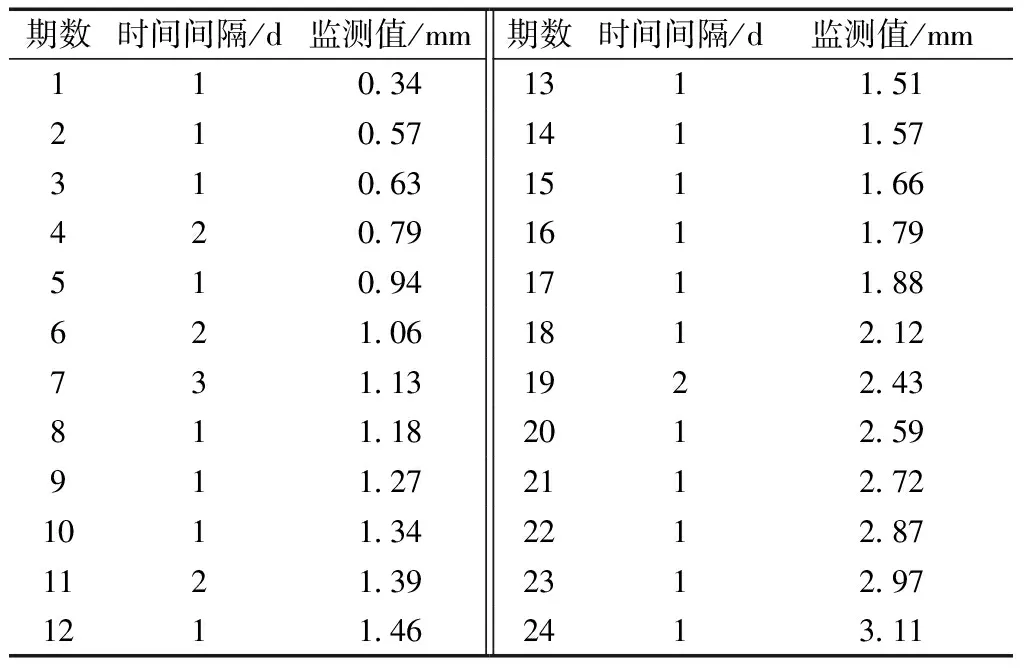
表7 算例2凍脹變形監測數據

由式(7)計算非等間距回歸模型擬合值與預測值。

3.2.3 權重系數計算與預測結果評價

由式(15)～式(18)計算灰色模型與回歸模型系數：ω1=0.479 6,ω2=0.520 4。

三種模型擬合、預測結果見表8、表9。

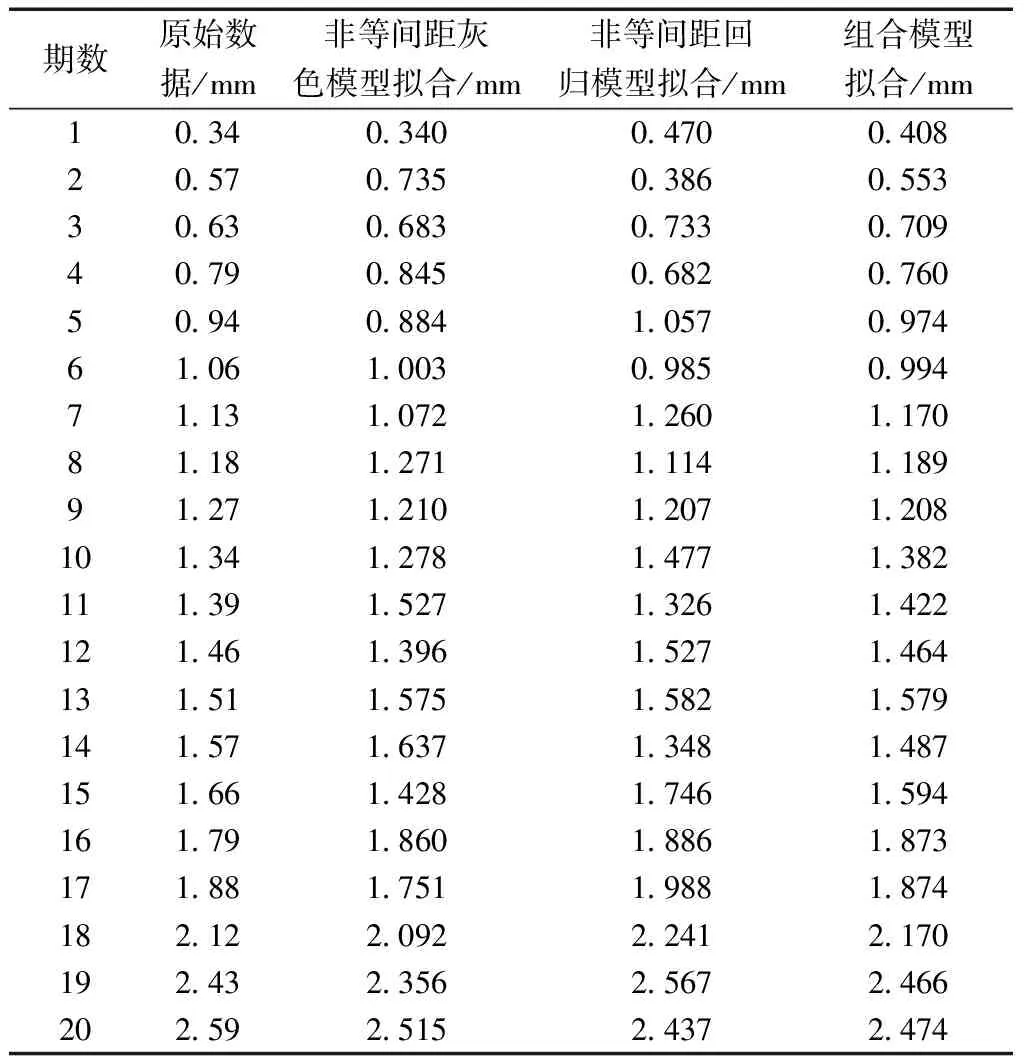
表8 算例2擬合結果對比

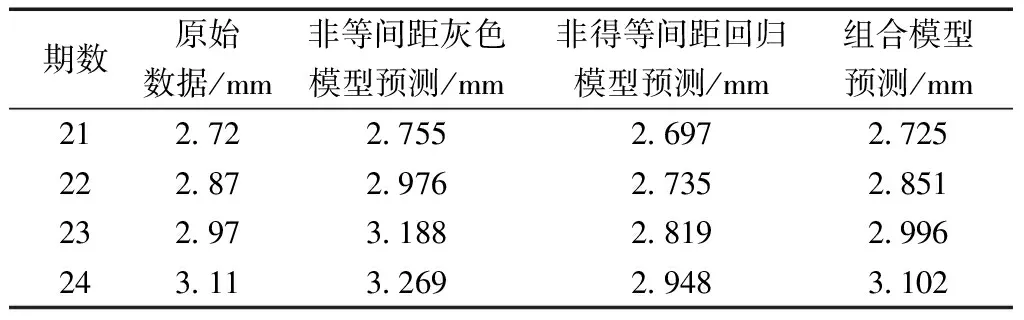
表9 算例2預測結果對比

3.2.4 模型等級、精度分析

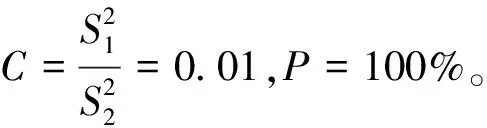
由表10可得,組合模型預測精度等級為一級。

由式(22)～式(24)及結合表8、表9中數據得3種模型誤差分布,如表10所示。三種模型對應的單項誤差數據變化情況如圖5～圖7所示。

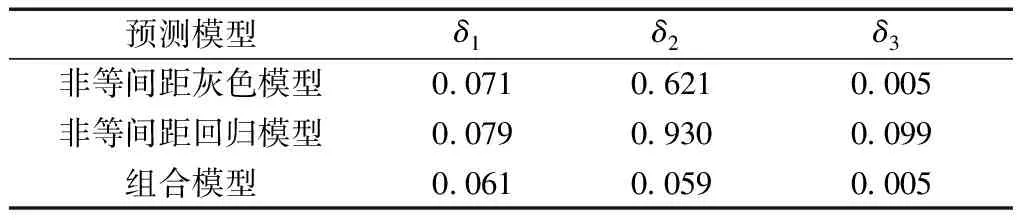
表10 算例2精度評價指標

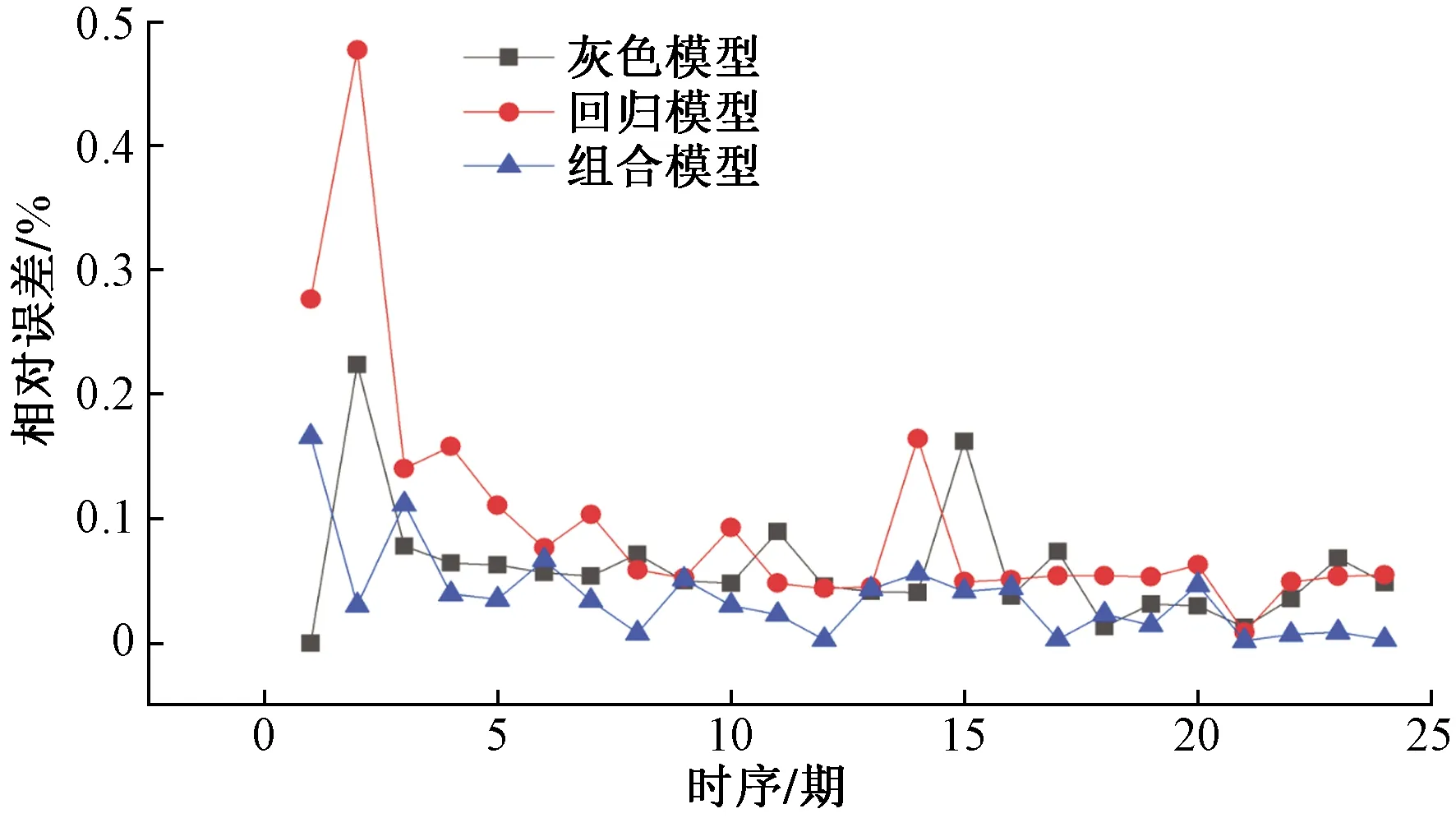
圖5 算例2相對誤差對比Fig.5 Relative error comparison of example 2

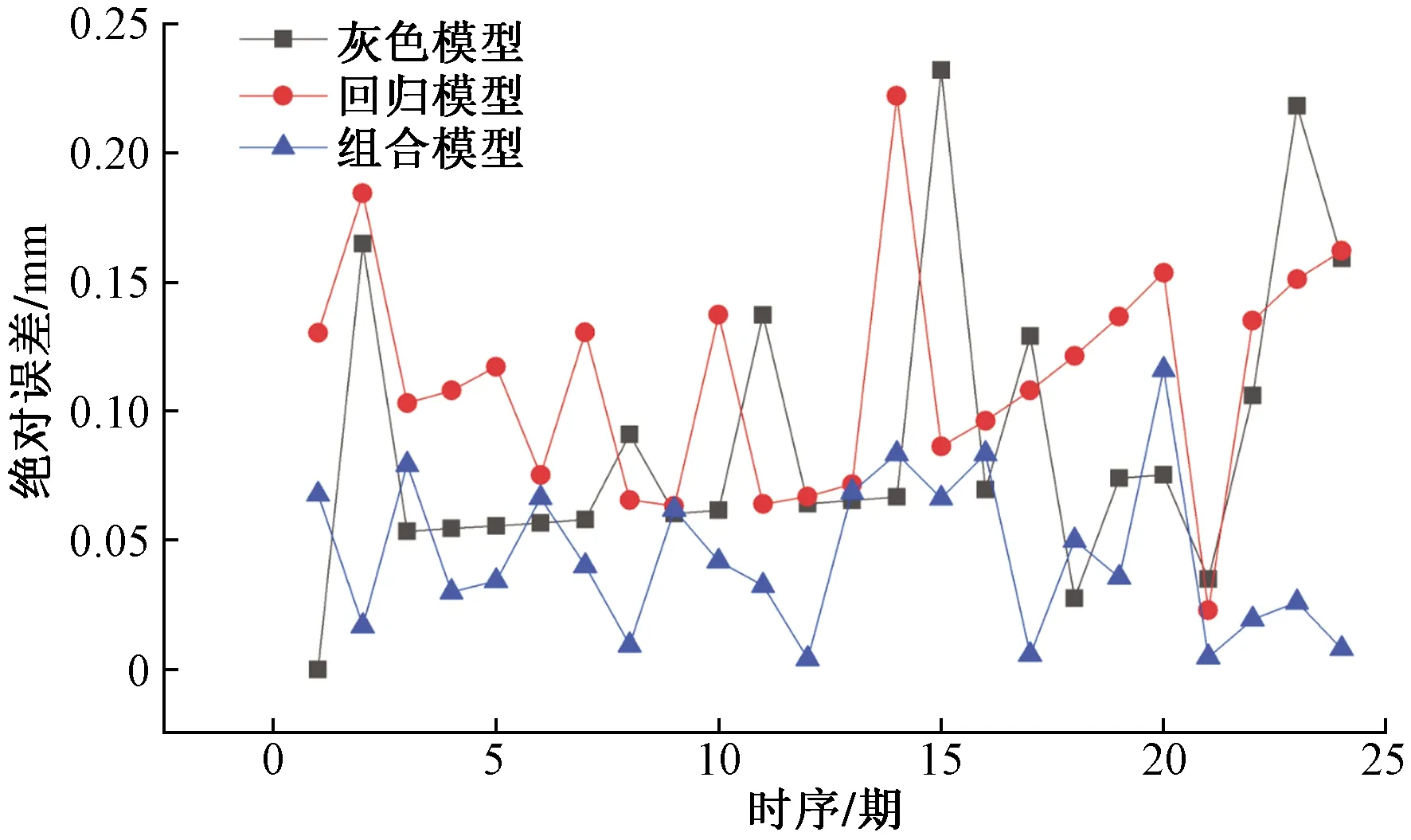
圖6 算例2絕對誤差對比Fig.6 Relative error comparison of example 2

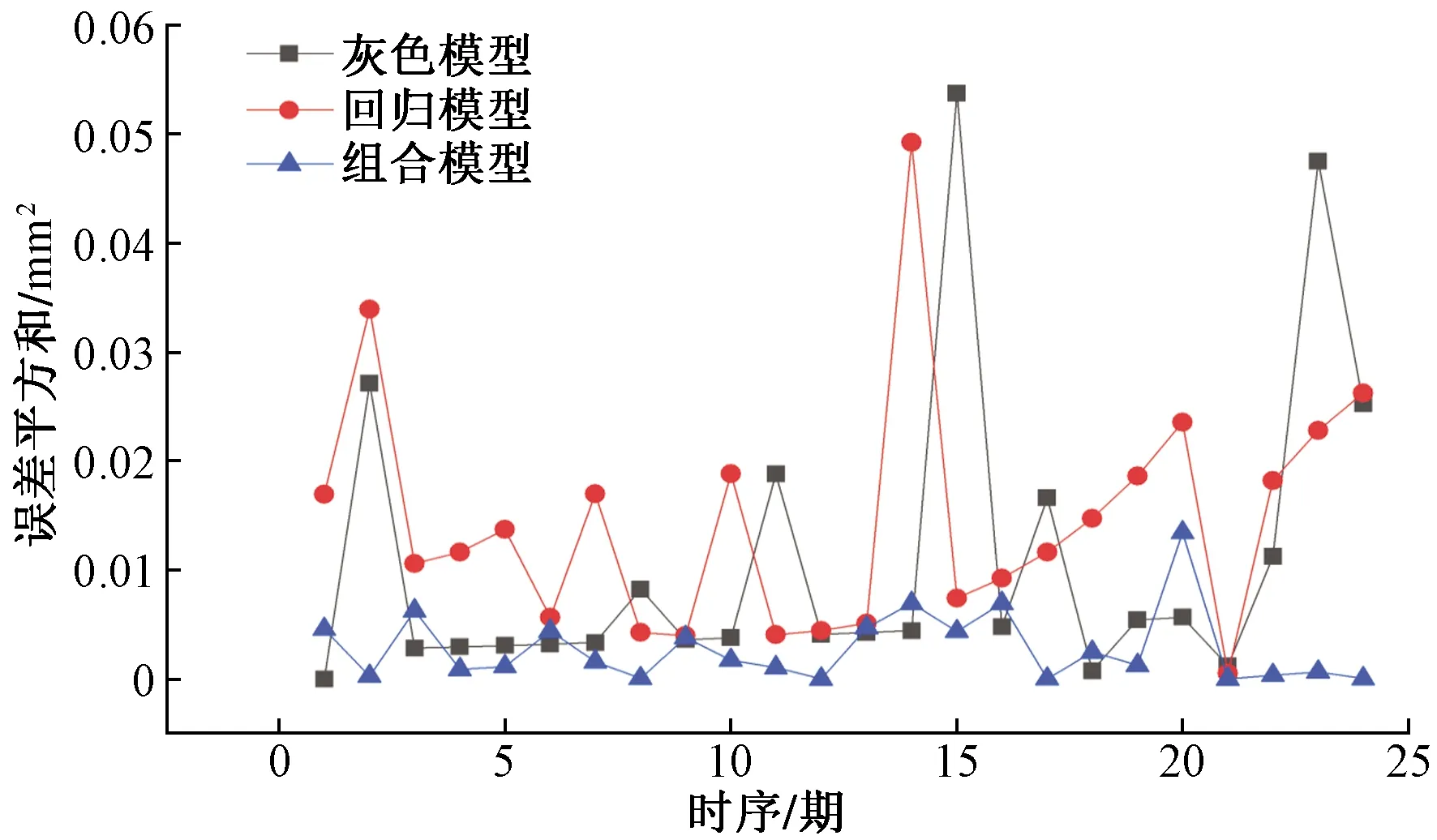
圖7 算例2誤差平方和對比Fig.7 Relative error comparison of example 2

由表10可得,組合模型平均誤差指標明顯小于非等間距回歸模型。圖5～圖7可以看出組合模型在相對誤差、絕對值誤差、平方和誤差三個方面明顯優于非等間距灰色模型與非等間距回歸模型。可以更好地為季節性凍土區的高鐵運營、運行安全提供保障

4 結論

本文提出組合模型針對高鐵路基凍脹監測數據進行預測研究，主要得出以下結論。

(1)利用馬爾科夫模型對非等間距灰色模型與非等間距回歸模型預測結果進行修正,提高了預測精度,由于模型本身局限性無法長期保持穩定性理想效果。

(2)以高鐵路基監測數據進行擬合預測分析,在預測馬爾科修正基礎上進行最優權組合預測,相對于單一的模型預測結果具有更好的穩定性,離散程度更低,準確度更高。采用組合模型擬合、預測高鐵凍脹變形降低了相對誤差、絕對誤差、誤差平方和。