機場滑行道橋橋面板橫向有效分布寬度分析

黃信, 譚成松, 陳宇, 吳堃, 李長輝

(中國民航大學交通科學與工程學院, 天津 300300)

大型機場多條跑道之間常采用滑行道橋進行連接，如成都雙流機場采用滑行道橋連接第一跑道和第二跑道。機場滑行道橋飛機通行頻繁，由于飛機輪載取值及尺寸和公路橋梁汽車輪載存在明顯差異[1-3]，為確保機場滑行道橋結構安全，應對飛機輪載作用下機場滑行道橋橋面板橫向有效分布寬度取值開展研究。目前針對組合橋面板的疲勞[4]、高性能材料橋梁受力機理[5]等方面開展了相關研究，而橋面板橫向有效分布寬度取值方面主要針對汽車輪載作用[6-11]。方志等[6]基于塑性理論分析得到了箱梁頂板的橫向受力有效分布寬度的取值方法；趙品等[7]研究了波形鋼腹板箱梁的橋面板有效分布寬度取值，分析表明依據現(xiàn)行公路橋規(guī)計算的有效分布寬度相比有限元和試驗結果略小；衛(wèi)軍等[8]研究了肋梁體系的荷載有效分布寬度在斜拉橋交叉梁體系橋面板上的適用性，并進一步分析了考慮橫梁變形的橋面板荷載有效分布寬度；喬鵬等[9]采用數(shù)值分析和試驗方法分析了單向多室波形鋼腹板箱梁的橫向受力，研究表明單向多室箱梁有效分布寬度可取0.9倍的單室箱梁有效寬度。可知，目前考慮橋面板構造形式、梁板滑移效應、結構非線性等因素研究了汽車輪載下混凝土橋面板的橫向有效分布寬度取值，而針對飛機輪載作用下機場滑行橋橋面板橫向有效分布寬度取值缺少相關研究，機場滑行橋橋面板橫向有效分布寬度取值仍采用公路橋規(guī)公式進行取值。為機場滑行道橋橋面板結構受力安全和設計提供依據，有必要分析飛機輪載下滑行道橋橋面板橫向有效分布寬度的取值。

相對現(xiàn)場原型試驗會影響機場運行而難以實施，而采用數(shù)值分析方法研究機場滑行道橋橋面板的有效分布寬度可以合理考慮材料非線性、飛機輪載類型等因素影響。現(xiàn)建立機場滑行道橋橋面板三維數(shù)值精細化分析模型，采用損傷塑性本構模型模擬混凝土材料的非線性特性，考慮飛機輪載構型差異影響，分析滑行道橋橋面板橫向有效分布寬度取值。

1 混凝土橋面板橫向有效分布寬度

1.1 橋面板橫向有效分布寬度的影響因素

飛機輪載尺寸會影響橋面板橫向有效寬度的取值，分析時應考慮不同飛機機型的輪載尺寸取值。現(xiàn)考慮大型、中型和小型三種機型飛機輪載對橋面板橫向有效分布寬度的影響；橋面板邊界條件對橫向分布寬度取值具有重要影響，分析機場滑行道橋采用T形主梁的簡支梁橋，橋面板為固結狀態(tài)。

1.2 橋面板橫向有效分布寬度計算

橋面板橫向有效分布寬度是一種等效寬度，局部荷載作用下橋面板橫向有效分布寬度計算公式為

(1)

式(1)中：a為橋面板橫向有效分布寬度；M為局部荷載所產生的板跨中截面的總彎矩；mxmax為荷載中心處的最大彎矩值。

1.3 飛機輪載模型

為分析機場滑行橋橋面板輪壓橫向分布機理及橫向有效分布寬度，應確定飛機輪載作用的取值。由于飛機起落架構型種類較多，并且飛機輪壓差別大，采用A380-800、B747-400和 A300機型考慮大型、中型和小型三種飛機輪載作用，三種飛機輪載作用參數(shù)如表1所列[1]。

表1 飛機荷載參數(shù)

主起落架一個機輪的靜載P計算公式為

(2)

式(2)中：G為飛機的最大起飛重量；KZ為主起落架的荷載分配系數(shù)，取0.97；m為主起落架個數(shù)；n為一個主起落架上的輪數(shù)。

對飛機輪胎接地面積進行簡化換算，飛機輪印尺寸計算公式為

(3)

式(3)中：L和W分別為換算后的矩形輪印的長和寬，mm；Pt為飛機主起落架單輪輪載，kN；q為胎壓，MPa。

根據式(2)和式(3)計算得到三種機型的單個輪載大小和尺寸如表2所列。

表2 飛機輪載取值及尺寸

2 滑行道橋橋面板數(shù)值分析模型

2.1 滑行道橋主梁及道面板尺寸及配筋

機場滑行道橋采用鋼筋混凝土簡支T形梁橋。橋面鋪裝采用11 cm的瀝青混凝土。T形梁的梁高為1.37 m，簡支梁計算跨度為18 m，橋梁混凝土標號為C40，鋼筋采用HRB335。滑行道橋的道面板跨中縱向鋼筋采用16@120 mm，支座縱向鋼筋采用18@120 mm，支座處板厚為210 mm，跨中處板厚為170 mm，垂直于縱向分布鋼筋采用10@150 mm，飛機輪載作用于橋面板跨中，滑行道橋梁板截面尺寸如圖1所示。

主梁和橋面板采用實體單元模擬，該單元為八結點線性六面體單元，采用減縮積分，可以對有限元沙漏進行控制。鋼筋采用桁架單元模擬，建立包括縱筋和箍筋的鋼筋籠。采用ABAQUS有限元軟件建立的機場滑行道橋三維有限元模型如圖2所示。

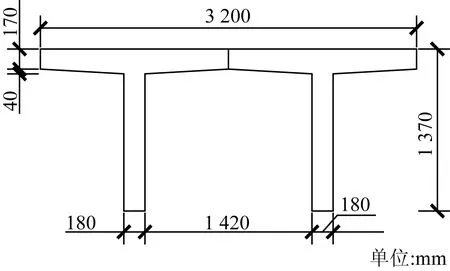
圖1 滑行道橋梁板截面尺寸Fig.1 Cross section dimension of beam and slab of taxiway bridge

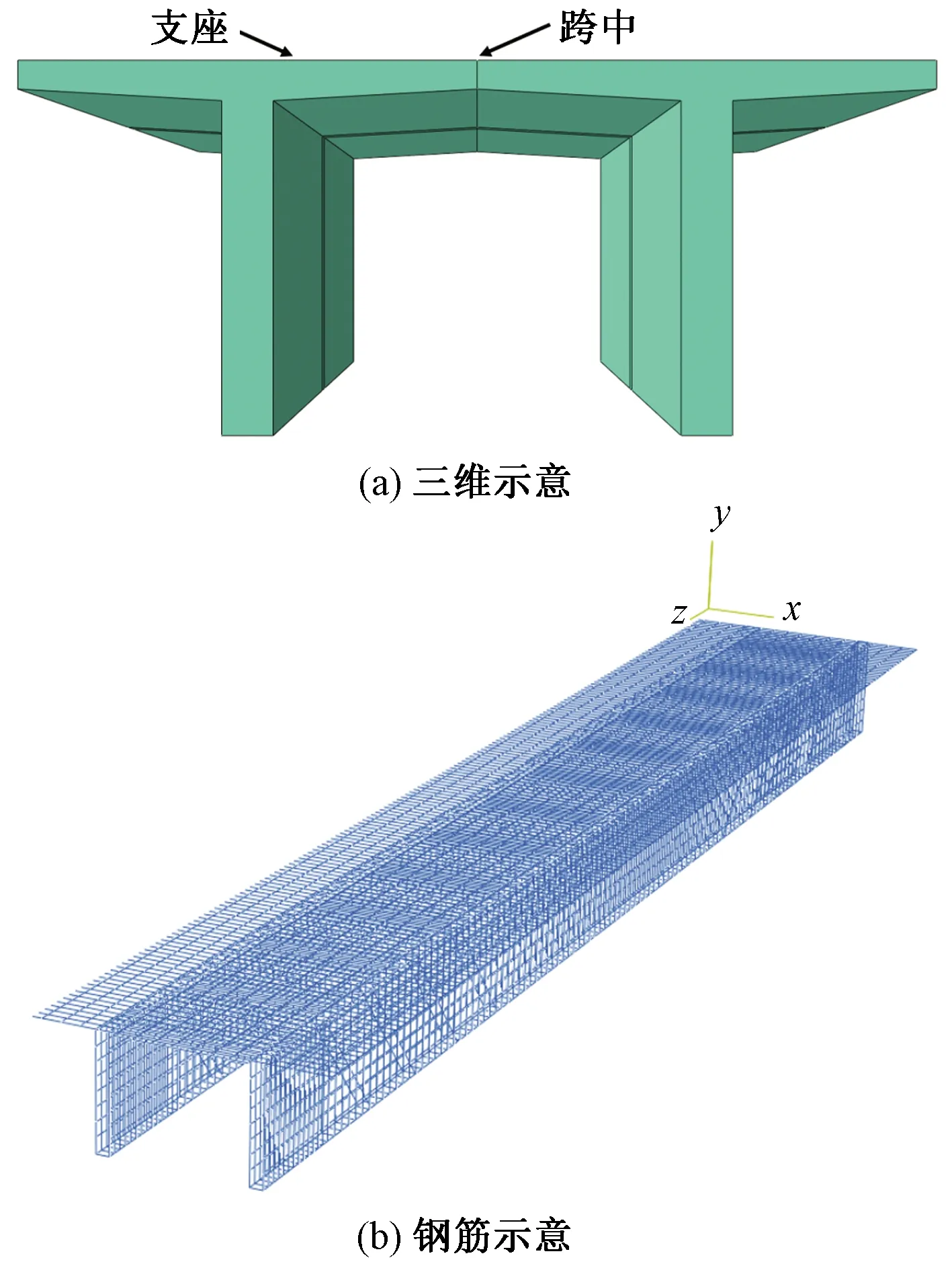
圖2 機場滑行道橋橋面板三維有限元數(shù)值模型Fig.2 3-D finite element numerical model of airport taxiway bridge deck

2.2 混凝土損傷塑性本構模型

采用損傷塑性本構模型模擬混凝土的非線性特性，該模型可以描述混凝土材料在受拉和受壓下的剛度退化、滯回荷載作用下的剛度恢復以及應變率的影響[10-11]。

通過修正初始彈性剛度考慮材料受力后發(fā)生的損傷，建立應力-應變關系為

(4)

混凝土材料采用損傷塑性本構模型，混凝土單軸損傷因子-應變關系如圖3所示(鋼筋采用理想彈塑性模型)。

圖3 混凝土單軸應力狀態(tài)下混凝土損傷因子-應變關系Fig.3 Damage factor-strain relationship of concrete under uniaxial stress

3 滑行道橋橫向有效分布寬度分析

滑行橋橋面板在跨中處為固結，考慮飛機輪載作用于板跨中。為明確材料非線性特性對飛機荷載作用對橋面板橫向有效分布寬度的影響，分析中混凝土和鋼筋材料分別考慮彈性材料和彈塑性材料兩種工況。

3.1 彈性狀態(tài)

在滑行道橋道面板跨中位置作用飛機輪載，分析滑行道橋道面板在飛機輪載作用下的應力狀態(tài)。為研究飛機輪載作用下滑行道橋橋面板的橫向有效分布寬度取值，取滑行道橋橋面板跨中處的上、下表面的混凝土的縱向應力即為橋面板跨度方向的應力進行分析。機場滑行道橋橋面板的混凝土縱向應力分布如表3所列和圖4所示。

表3 飛機輪載作用下彈性狀態(tài)機場滑行道橋橋面板上表面混凝土應力Table 3 Concrete stress on the deck of taxiway bridge in elastic state by the aircraft wheel load action

圖4 飛機輪載作用時彈性狀態(tài)機場滑行道橋橋面 板混凝土應力分布Fig.4 Stress distribution of deck concrete of taxiway bridge in elastic state by the aircraft wheel load action

通過表3和圖4可知，在彈性狀態(tài)下，飛機輪載作用于滑行橋橋面時結構應力隨著距飛機輪載作用位置距離的增加而應力逐漸減小，如A380飛機輪載作用時對于行車道板上表面的距離為0.3 m處的混凝土應力為5.5 MPa，而距離為0.8 m處時混凝土應力為2.7 MPa。

同樣可知，對于A380、B747和A300三種機型輪載作用下的行車道面板的應力分布趨勢較為一致，在距離飛機輪載較近處混凝土應力降幅較為明顯，隨時距離飛機輪載距離的增大混凝土應力降幅減緩。

采用式(1)計算得到的飛機輪載作用下機場滑行道橋橋面板的橫向有效分布寬度如表4所列，同時列出了根據公路橋規(guī)計算得到橋面板橫向有效分布寬度。

表4 飛機輪載作用時彈性狀態(tài)機場滑行道橋橋面板 橫向有效分布寬度

通過表4可知，對于彈性狀態(tài)，當飛機輪載作用于道面板跨中時，數(shù)值分析得到的道面板橫向有效分布寬度較規(guī)范計算值增大，如A380飛機輪載作用下通過道面板上表面的混凝土應力計算得到的橋面板的有效分布寬度為1.64 m，而采用公路橋規(guī)計算得到的橋面板的橫向有效分布寬度為1.35 m，增幅為18%，說明采用公路橋規(guī)方法計算得到的橋面板橫向分布寬度取值較為保守。同時可知，對于彈性狀態(tài)下，采用道面板上表面和下表面的混凝土應力計算得到的橫向分布寬度取值較為一致，如A380飛機輪載作用下通過道面板上表面混凝土應力得到的橫向有效分布寬度為1.60 m，而通過道面板下表面混凝土應力得到的橫向有效分布寬度為1.64 m，對于B747和A300機型可以得出類似結論。

3.2 彈塑性狀態(tài)

考慮飛機輪載作用時滑行道橋橋面板結構會進入彈塑性受力狀態(tài)，采用彈塑性本構模擬鋼筋和混凝土的非線性特性，分析彈塑性狀態(tài)下飛機輪載作用時機場滑行道橋橋面板的橫向有效分布寬度取值。圖5給出了飛機輪載作用下機場滑行道橋橋面板下表面的橫向分布節(jié)點的混凝土的拉應力曲線，其中1點位于飛機輪載作用位置的中點，2～10點距飛機輪載中點的距離按0.2 m的幅值增加。

圖5 飛機輪載作用時彈塑性狀態(tài)機場滑行道橋橋面板 下表面混凝土應力分布Fig.5 Stress distribution of concrete under the deck in elastic-plastic state of airport taxiway bridge

通過圖5可知，當考慮混凝土和鋼筋的塑性時，在飛機輪載逐漸施加過程中距離輪載較近的1點和2點最先達到混凝土抗拉應力峰值，然后出現(xiàn)剛度退化而開始卸載、應力降低，此時相鄰的3點和4點應力逐漸增大，可以看出3點和4點在飛機輪載施加而達到最大值時1～3點出現(xiàn)卸載，而4～7點應力接近峰值，8～10點應力一直增大而尚未達到峰值，通過上述橋面板橫向不同位置處的混凝土應力分布，表明考慮材料非線性時混凝土應力沿橋面板橫向出現(xiàn)了內力重分布現(xiàn)象。

此時為分析機場滑行道橋橋面板的橫向有效分布寬度，對橋面板的鋼筋應力分布進行分析，彈塑性狀態(tài)下飛機輪載作用下機場滑行橋道面板鋼筋應力分布如表5所列和圖6所示。

通過表5和圖6可知，在彈塑性狀態(tài)下，飛機輪載作用于滑行橋橋面板跨中時，鋼筋應力隨著距飛機輪載距離的增加出現(xiàn)鋼筋應力逐漸減小，如A380飛機輪載作用時對于行車道板上表面的距離為0.24 m處的鋼筋應力為67 MPa，而距離為0.84 m處時鋼筋應力為25 MPa；同時可知，鋼筋的應力減幅隨距離飛機輪載中心位置的增大而降低；對于B747和A300機型也可得出類似結論。

根據式(1)計算得到飛機輪載作用下機場滑行道橋橋面板的橫向有效分布寬度如表6所列，其中彈性狀態(tài)為道面板下表面混凝土應力計算的橫向有效分布寬度。

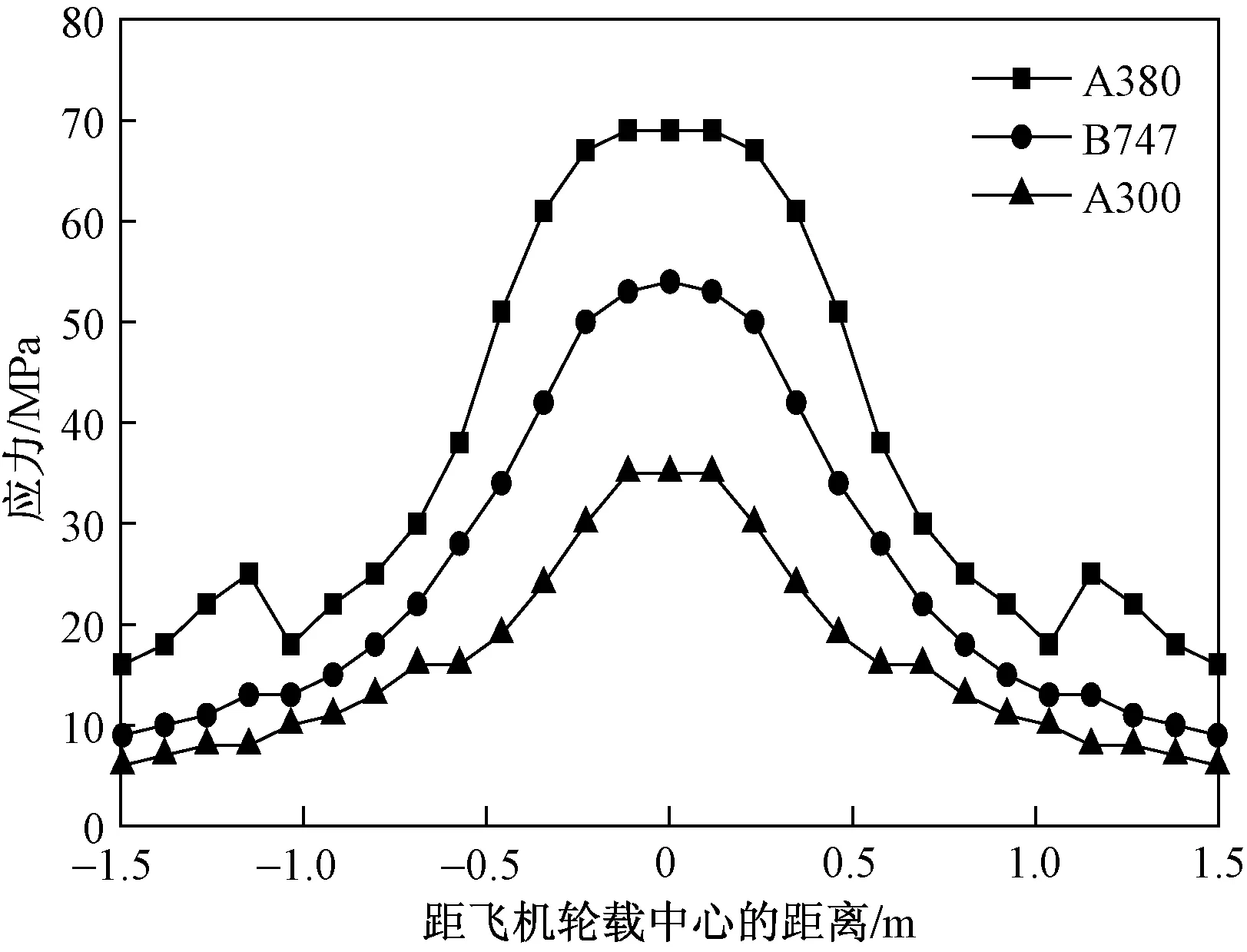
圖6 飛機輪載作用時彈塑性狀態(tài)機場滑行道 橋橋面板鋼筋應力分布Fig.6 Rebar stress distribution of taxiway bridge in elastic-plastic state by the aircraft wheel load action

通過表6可知，考慮材料彈塑性，當飛機輪載作用于道面板跨中時，通過數(shù)值分析得到的道面板橫向有效分布寬度較規(guī)范計算值增大較多，如A380飛機輪載作用下計算得到的橋面板的有效分布寬度為1.78 m，而采用混凝土橋規(guī)計算得到的橋面板的橫向有效分布寬度為1.35 m，增幅為24%。

考慮材料彈塑性性能時計算得到的橋面板的橫向有效分布寬度較彈性材料而言增大，如A380飛機輪載作用下，采用彈塑性材料計算得到的橋面板的橫向有效分布寬度為1.78 m，而采用彈性材料時計算得到的橫向有效分布跨度為1.64 m，增幅為8.5%，這主要是由于橋面板在飛機輪載作用下局部區(qū)域發(fā)生塑性而出現(xiàn)應力重分布，使飛機輪載的橫向有效分布寬度較彈性狀態(tài)增大，所以對于飛機等大荷載作用下橋面板橫向有效分布寬度分析應考慮材料的非線性特征。

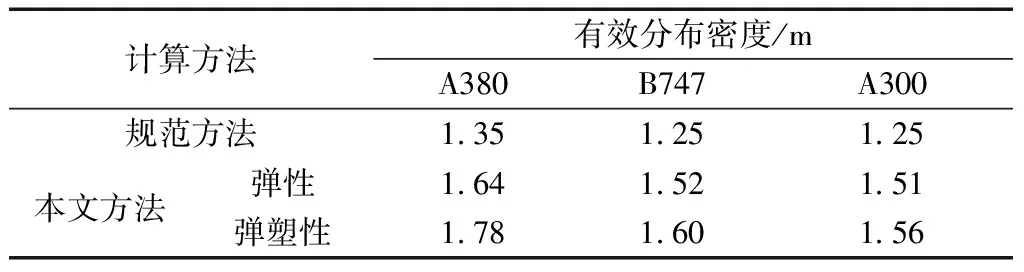
表6 飛機輪載作用時彈塑性狀態(tài)機場滑行道橋橋面板 橫向有效分布寬度Table 6 Effective transverse width of deck of taxiway in elastic-plastic state by the aircraft wheel

表5 飛機輪載作用時彈塑性狀態(tài)機場滑行道橋橋面板鋼筋應力

4 結論

建立機場滑行道橋橋面板三維有限元數(shù)值精細化分析模型，考慮材料非線性影響，分析了飛機輪載作用下滑行橋橋面板的橫向有效分布寬度取值。通過分析得出如下結論。

(1)采用三維數(shù)值精細化分析方法計算得到的飛機輪載作用下滑行橋橋面板的橫向有效分布寬度較公路橋規(guī)計算值增大，如材料彈性狀態(tài)下飛機輪載作用于橋面板跨中時橫向有效分布寬度的增幅為18%，表明目前采用公路橋規(guī)計算的橋面板橫向有效分布寬度取值偏于保守。

(2)橋面板橫向有效分布寬度取值隨飛機輪載作用大小不同而存在差異，如材料彈性狀態(tài)下A380和B747飛機輪載作用于橋面板跨中時橫向有效分布寬度分別為1.64 m和1.52 m。

(3)當考慮飛機輪載作用下橋面板進入塑性受力時，橋面板橫向有效分布寬度計算值較考慮材料彈性狀態(tài)而言增大，如當飛機輪載作用橋面板跨中時橫向有效分布寬度的增幅為8.5%，由于飛機等大型輪載作用下橋面板處于非線性受力階段而出現(xiàn)內力重分布，所以計算飛機輪載下滑行道橋橋面板的橫向有效分布寬度取值時應考慮材料非線性。