“錯位相減法”求和問題的另一突破路徑探討
蔣彥磊
(南京市江寧高級中學,江蘇 南京 211100)
數列求和問題一直是高考中一類比較常見的題型,是高考中的熱點與重點之一。對于“等差*等比”型的數列求和,傳統的方法是“錯位相減法”,該方法雖操作過程簡單,但式子變形技巧強、關鍵點多、對學生的運算能力要求高等,學生經常不小心就出錯。本文筆者從另一視角探究解決此類型數列求和的其他一般性解法,供大家參考。
一、問題的提出
數列是高考考查的重點內容,主要考查學生的運算求解能力,無論是小題還是解答題都有所涉及,尤其是數列求和問題涉及的知識點多、方法多、綜合性強等對學生的能力要求高,很多學生常因解答過程繁雜、運算能力弱導致失分。若能轉換因方法多樣、題型靈活問題解決的視角,認清本質也可以簡化運算,提高解題效率。以下面問題為例:
(2020 全國3 理17)設數列{an}滿足a1=3,an+1=3an-4n。
(1)略;(2)求數列{2n·an}的前n項和Sn。
此題,第(1)問是典型的構造數列求通項問題,根據遞推式的結構特點,考慮到兩邊加上一個等差數列的相鄰項即可構造特殊數列{an-2n-1}為常數列,從而得an=2n+1。第(2)問是數列求和問題,通項公式為“等差*等比”型,通常利用錯位相減法可以得出結果Sn=(2n-1)·2n+1+2。但通過以往的教學可以知道,錯位相減法容易理解,且操作過程固定,學生易于掌握,但因計算量大,注意點多,學生經常出錯,有些老師也會錯誤地引導,認為解決此類數列求和的方法只有這一種,讓學生遇到此類問題總有一種“自古華山一條道”感覺,戰戰兢兢地算下去。但數列的本質特點是按照一定次序排成的一列數,項與和之間本質上可以直接轉化,所以,對于問題(2)是不是可以借助項和關系可參考問題(1)的方法構造新數列解決呢?
二、問題的解決
由項和關系式易知:當n≥ 2時即觀察:數列{(2n+1)·2n}是由等差數列{(2n+1)}與等比數列{2n}相乘構造,可嘗試把數列{(2n+1)·2n}拆分成兩個相同結構的一個數列的相鄰兩項的差,再直接構造與Sn有關的新數列,間接得到Sn。
(一)嘗試構造,解決問題
解:(1)an=2n+1;
利用待定系數法,令
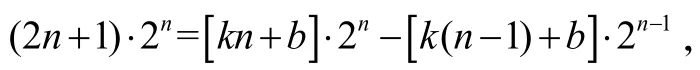
對應系數相等得k=4,b=-2.
所以,(2n+1)·2n=(4n-2)·2n-(4n-6)·2n-1,n≥2.
記bn=(4n-2)·2n.則 (2n+1)·2n=bn-bn-1,n∈N*且n≥2.
所以,Sn=Sn-1+bn-bn-1,n≥ 2.即Sn-bn=Sn-1-bn-1,n≥2.
又當n=2時,S2-b2=S1-b1=2.
所以數列{Sn-bn}為常數列,即Sn-bn=2,n∈N*.所以,
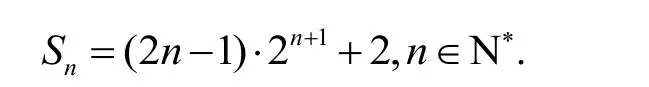
(二)優化解法,發現本質
在前面,構造關于與Sn有關的新數列的過程中,得到Sn=Sn-1+bn-bn-1,n≥ 2.即
Sn-Sn-1=bn-bn-1,n≥ 2.所以,求和過程還可以做“裂項”處理:
(接方法 一)因為bn=(4n-2)·2n,則(2n+1)·2n=bn-bn-1,n∈N*且n≥ 2.又 當n=0,1時也成立。所以

其實上述解決問題的兩個角度是有必然聯系的,都可以歸為裂項變形策略,下統稱為“裂項法”。由于數列通項的特點是等差數列*等比數列,考慮到等差數列通項公式的特點及推導方法(裂項疊加消元),也可把通項變形為有相似結構的數列相鄰兩項的差,如:[a(n+1)+b]·qn+1-(an+b)·qn,再利用待定系數法確定系數,就可以順利將錯位相加法求和問題轉化為裂項相消解決,大大減少了運算難度,且不容易出錯。只是在確定系數時要細心計算,對求得的檢驗一下,確保無誤再繼續求和。該方法更接近問題的本質,相比于“錯位相減法”的計算過程,運算過程更優化,學生更容易算對,這不僅能提升學生學好數學的信心,拓寬了學生的思維,也提醒老師在日常教學中引導學生多視角思考問題,多角度解決問題。同時也給老師的教學研究提供了新的思考點,更有利于培養學生的數學核心素養和關鍵能力。
三、問題的引申
(一)結論
一般模型數列{(an+b)·qn}其中a≠0,q≠0 且q≠1 的前n項和為Sn,則
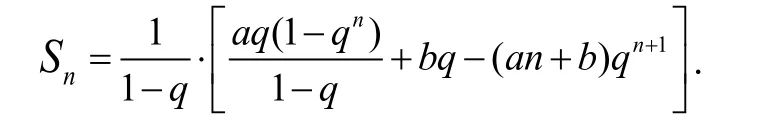
證明:
記數列{(an+b)·qn}其中a≠ 0,q≠ 0且q≠ 1的前n項的和為Sn。由錯位相減法可以得到
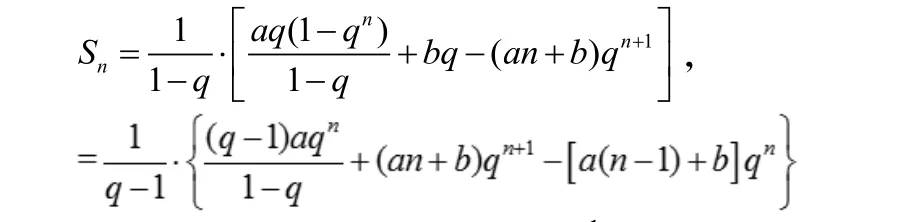
考慮到Sn中含有代數式參考引例,下用裂項法處理通項。
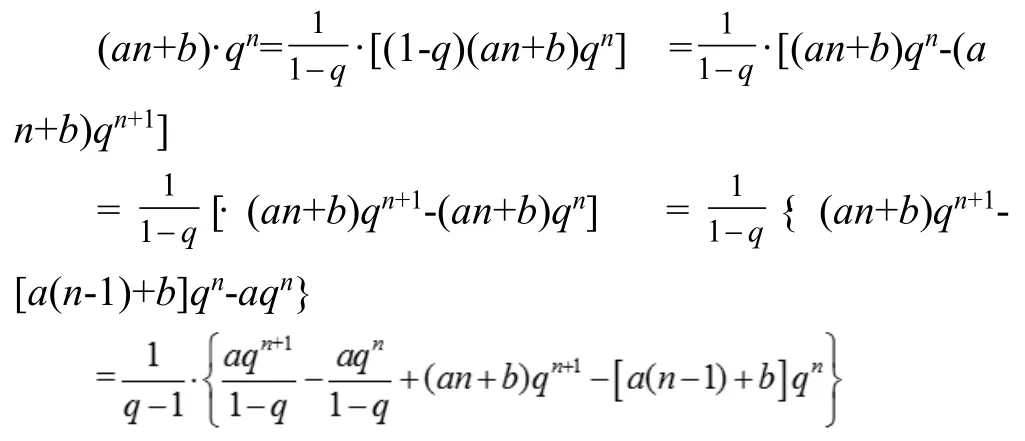

結論:“裂項法”對于一般數列{(an+b)·qn}其中a≠0,q≠0 且q≠1 的求和問題都適用。該方法更接近求和問題的本質,相比于以往常規的計算方法,運算過程學生更容易接受,解題思維也更加流暢自然。
(二)引申
對于一 般模型數列 {(an2+bn+c)·qn}其 中a≠ 0,q≠ 0且q≠ 1的求和問題是否適用?
下面以一道具體事例進行探究:
例.求數列{(n2+n)·2n}的前n項的和Sn。
解法1:依然利用待定系數法,令
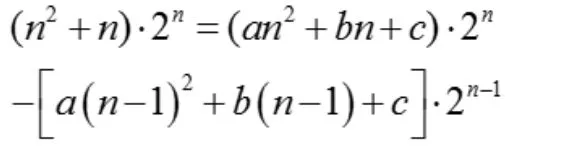
展開,對應系數相等,容易得到

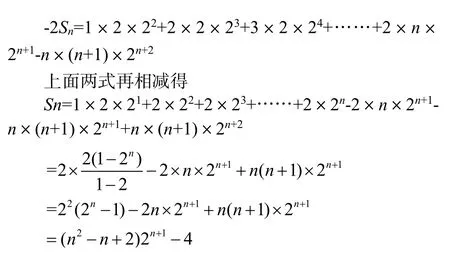
由此看來,“裂項法”也可以解決此類數列的求和問題,對于一般模型的驗證過程,請有興趣的讀者可以試試。解法2 兩次使用錯位相減最終得到答案,進一步說明了“裂項法”與錯位相減法的本質一致,方法同源,也進一步說明了這兩種方法的普適應和統一性。
四、反思
(一)“裂項法”的一般性
從前面的典例研究過程中,不難發現,“裂項法”對于多項式數列*等比數列型的數列求和即an=(bm-1nm-1+bm-2nm-2+……+b1n+b0)qn型的數列求和問題都適用。下面以m次多項式*等比數列為例介紹一般操作方法:我們只研究q≠ 1的情形,設an=(λm-1nm-1+λm-2nm-2+……+λ1n+λ0)qn-(λm-1(n-1)m-1+λm-2(n-1)m-2+……+λ1(n-1)+λ0)qn-1將上式打開,按照降冪規則合并同類項,整理成如下形式:an=(μm-1nm-1+μm-2nm-2+……+μ1n+μ0)qn。其中μ0,μ1,……μm-1是用λ0,λ1,……λm-1,q來表示的一次式。利用對應系數相等得到一個m元一次方程組,用代入法可以解出λ0,λ1,……λm-1,接著用“裂項法”即可求出數列{an}的前n項和Sn=(λm-1nm-1+λm-2nm-2+……+λ1n+λ0)qnλ0不難看出,當多項式次數較高時,錯位相減法就顯得非常復雜了,“裂項法”的優越性就顯而易見。
(二)裂項法使用的要點
裂項法在使用過程中需注意以下幾點:
1.待定系數法確定裂項系數時,最好根據通項結構進行選擇。如等。
2.選擇不同的相鄰項,對于下標n的取值有不同要求。如,引例法2 裂項求和中,最終n的取值需要從0開始,而變式1 中的n取值從1 開始。
3.無論哪一種方法,都要有首項驗證的意識。
(三)從思想方法上看,數列求和的本質就是消項。
大家知道連續函數的定積分,根據牛頓—萊布尼茨公式,可以求出原函數后作差,而數列是離散型的函數,且“(xn)'=n·xn-1”因此形如{(an+b)·qn}類數列求和也可轉化為“差”的形式。如:
(an+b)·q n=anq n+bq n=aq·(nqn-1)+bqn,這樣問題轉化為一個特殊數列{n·qn-1}和一個等比數列的求和問題,只要求出特殊數列{n·qn-1}的前n項的和,即可解決問題。在式子n·qn-1中,把q視作變量,聯想到導數公式(xn)'=n·xn-1,故還可以用導數法來解決求和問題。
所以從數學本質上看,數列求和的根本方法是“裂項相消”(差分求和),故本文討論的方法具有普適性。
通過以上討論不難發現,在數列求和問題中,雖方法多樣,但一定要看清本質,靈活選擇。相比于傳統方法,“裂項法”運用靈活廣泛,思路簡潔清晰,計算化繁為簡,學生不容易出錯,在掌握好錯位相減法的基礎上,再引導學生通過對數列通項的特征進行觀察比較、挖掘通項本質內涵,更能進一步理解解題的思想和方法,增強解題能力和自信,從而有利于學生數學學科核心素養的培育。另外,新高考更注重對學生學科關鍵能力的考查,這就要求老師在課堂教學中,要有意識地引導學生多角度思考問題,經歷多方法解決問題尤其是典型問題的探究過程不僅要實更要廣,這不僅有助于加深老師對學科內容的理解也促使著學生在解題過程中形成有規律的程序化的解題思路,優化解法和快速準確解題,也提升了學生的數學邏輯思維能力和數學運算能力,還能讓學生開拓了數學視野、堅定了學好數學的信心,更有利于學生的持續發展和多元發展。

