次分數布朗運動機制下具有浮動敲定價格的亞式期權定價
王竟莘,王欣怡,郭志東
(安慶師范大學數理學院,安徽 安慶 246133)
0 引言
期權定價一直是金融數學領域的熱點問題.自經典定價模型Black-Scholes模型被BLACK和SCHOLES[1]提出以來,研究者們通常用幾何布朗運動和分數布朗運動作為驅動源驅動標的資產價格,取得了大量研究成果.韓利華等[2]基于幾何分數布朗運動,利用保險精算方法求得亞式期權定價公式.于文明等[3]建立混合分數布朗運動和不變方差彈性的亞式期權定價模型,利用漸進展開方法給出了期權定價公式,對赫斯特指數和漸進逼近值進行數值分析.陳聰等[4]給出了在幾何布朗運動下的算數平均半亞式期權定價的近似半解析法,進一步利用對偶變量技術減少該方法的計算時間.KAHALé[5]運用多層次蒙特卡洛方法計算到期日的亞式期權價格,并將此方法與Milstein格式(由標量隨機微分方程驅動的過程)、Euler格式(由多維隨機微分方程驅動的過程)相結合,數值結果表明該方法優于傳統的蒙特卡洛算法.LU等[6]研究了基于不確定理論的亞式期權定價問題,利用期望值和樂觀值給出了亞式期權的定價公式,通過數值實驗驗證了結果的有效性.王偉[7]建立分數布朗運動下的亞式期權定價模型,利用無套利原理,經過Markov調制求得具有固定敲定價格的亞式看漲和看跌期權定價公式.沈明軒[8]建立了混合分數布朗運動下的冪型幾何平均亞式期權定價模型,利用擬條件期望給出其定價公式并推廣到支付紅利情況下.ZHANG[9]建立了分數布朗運動下帶有交易費和支付紅利的亞式期權定價模型,利用無套利原理和分數公式,給出了幾何亞式期權的定價公式和看漲-看跌平價公式,通過數值計算討論赫斯特指數和到期日對期權價格的影響.
2004年,BOJDECKI等[10]提出次分數布朗運動,相較分數布朗運動,次分數布朗運動具有協方差隨時間的增加而迅速衰減、增量在非重疊區間內的相關性較弱、同樣具備相似性和長程相關性的特點,因此次分數布朗運動更適合應用于金融市場.許多學者進行了相關研究,程潘紅等[11]建立了該環境下支付連續紅利的可分離交易可轉債定價模型,利用Mellin變換得到了顯示公式,通過數值模擬分析交易可轉債價格隨參數變化的趨勢.梁喜珠等[12]利用隨機分析理論和保險精算方法,建立該環境下的最值期權定價模型并求得定價公式,通過數值計算對市場不同的分形結構對期權價格的影響進行分析.劉曉敏[13]建立了單資產多噪聲的最優投資組合模型,利用隨機分析理論給出了次分數布朗運動下最優投資組合的顯示公式.然而,上述研究并未探討次分數布朗運動機制下具有浮動敲定價格的幾何亞式期權定價問題,本文將對該問題進行研究.
1 次分數布朗運動和亞式期權
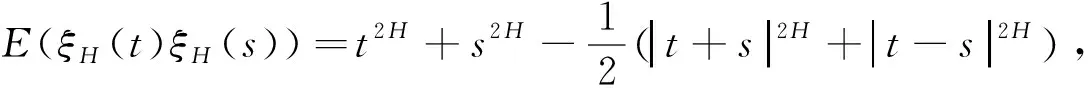
(i)自相似性:當a>0時,有{ξH(at),t≥0}{aHξH(t),t≥0};
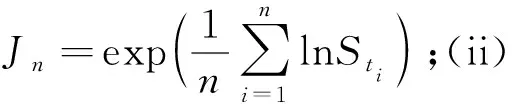
2 次分數布朗運動機制下具有浮動敲定價格的亞式期權定價
基于偏微分方法,討論次分數布朗運動下具有浮動敲定價格的幾何平均亞式期權定價問題.考慮Black-Scholes模型的次分數形態,即簡單金融市場模型下,其標的資產價格St滿足:
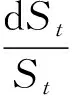
(1)
引理2.1[15]若函數f(t,ξH(t))為一個二元微分,則次分數布朗運動有It公式:
(2)
證明
定理2.1 假設標的資產價格St符合(1)給出的模型,則該亞式期權的V(t,S,J)價格滿足偏微分方程
(3)
且終值條件滿足:
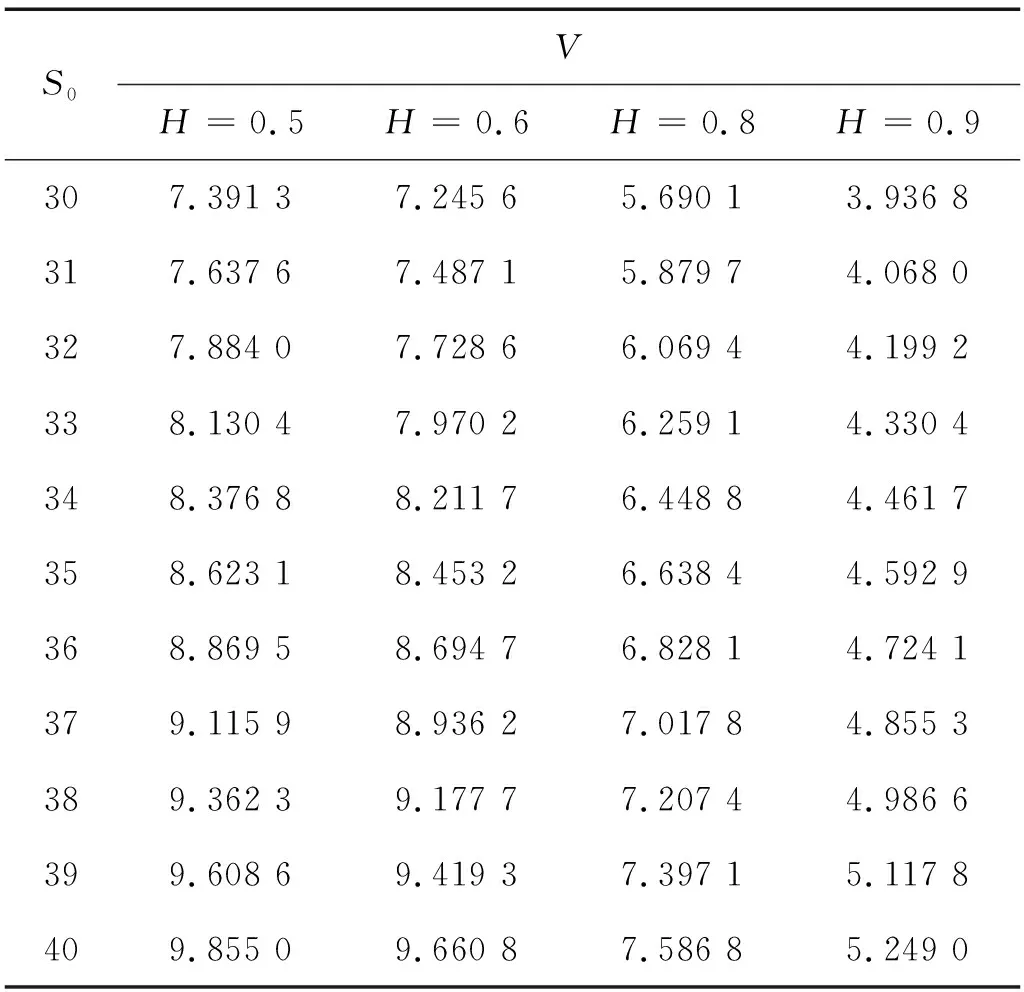
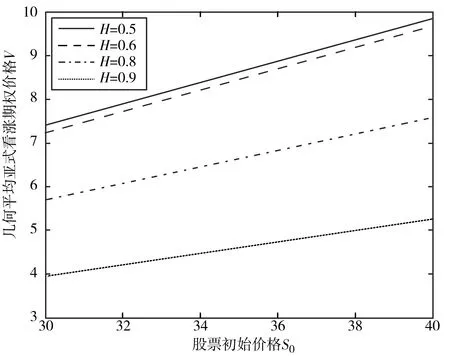
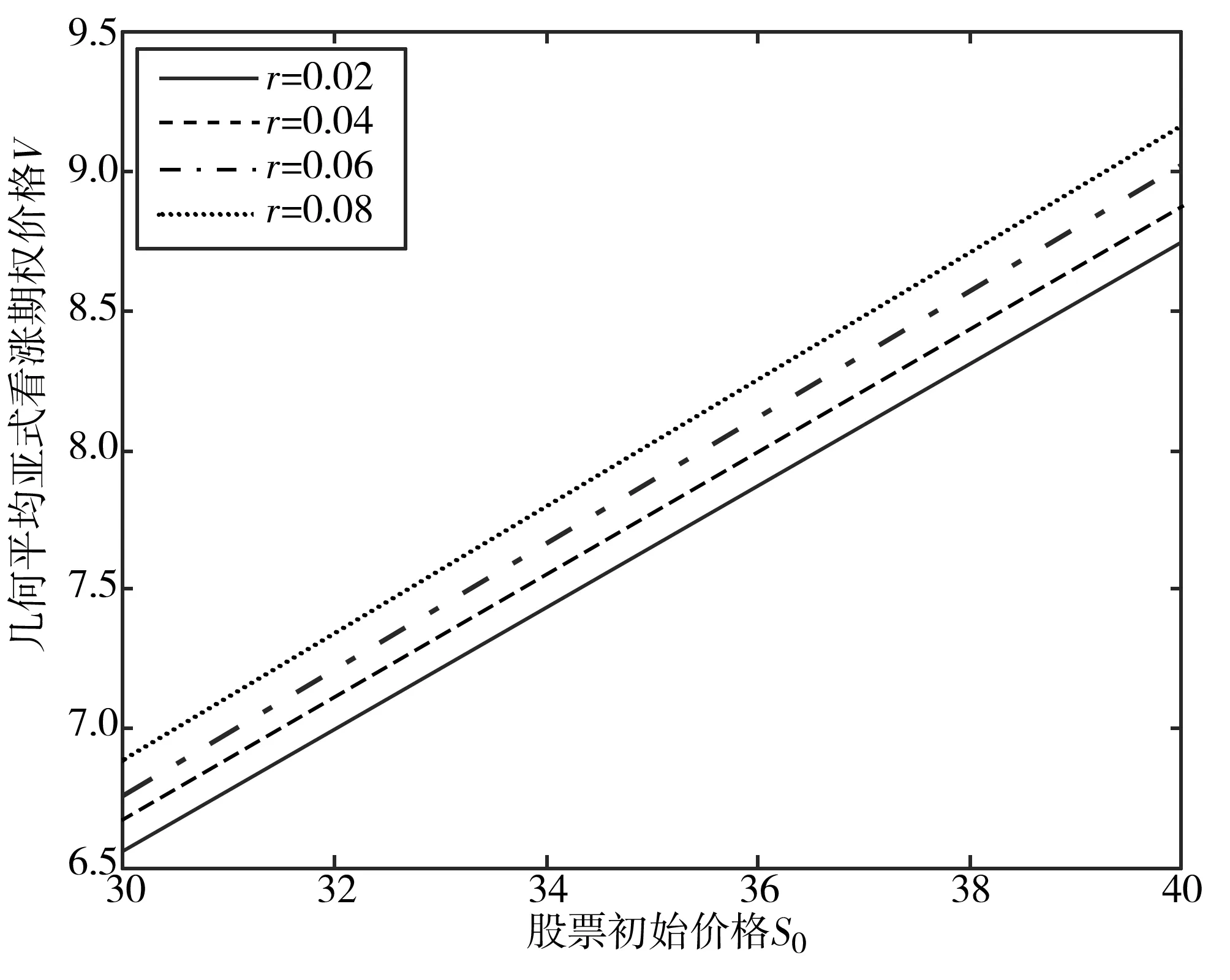
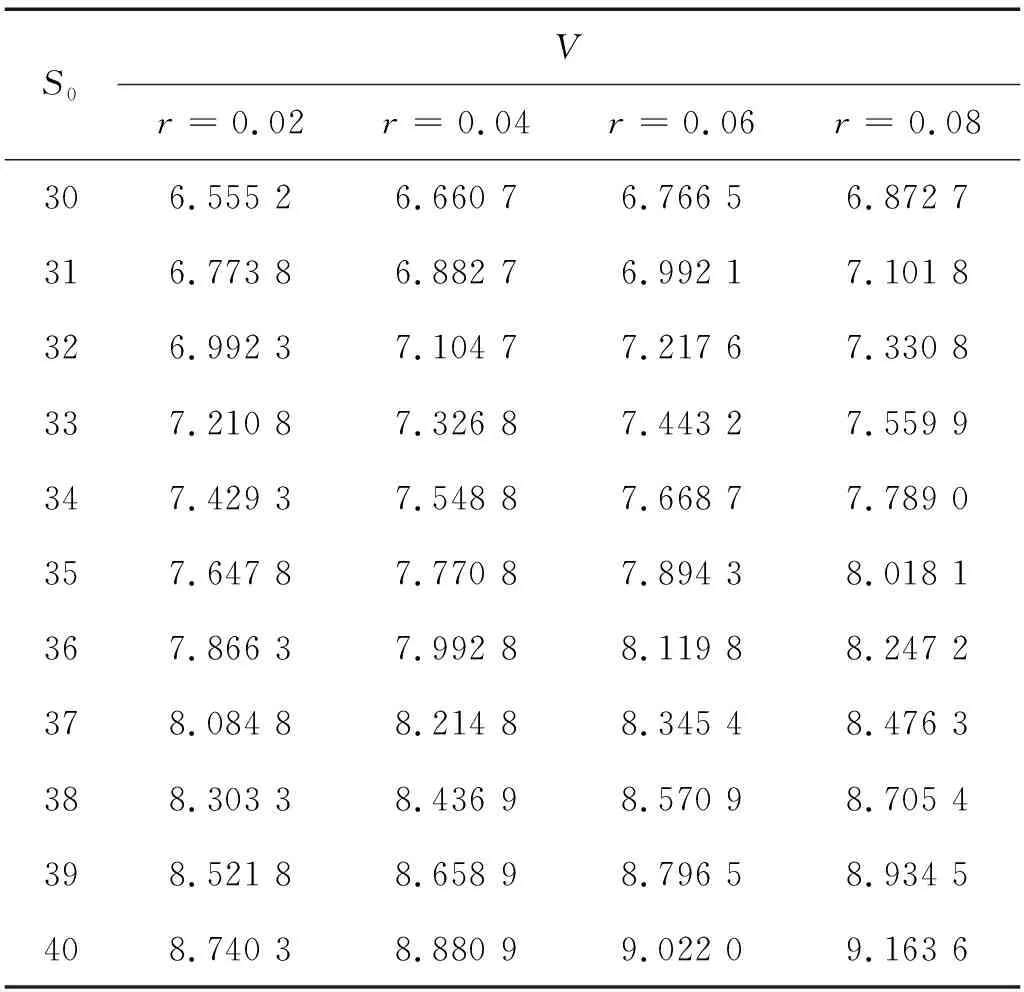
V(T,S,J)=(S-J)+,0 (4) 證明 考慮一個復制的投資組合Π包含一份期權Vt(t,St,Jt)和Δ份股票.在t時刻這個投資組合的價值為Π=V-ΔS. 假設Δ在時間區間(t,t+Δt)內沒有變化,則我們選擇合適的Δ,使Π在時間區間(t,t+dt)內無風險. dΠ=dV-ΔdS= (5) dΠ=rΠdt=r(V-ΔS)dt, 可得 (6) (7) 替換(7)到(6)中,可得 (8) 則定理2.1得證. 若求解偏微分方程(3)和終值條件(4),可得如下定理. 定理2.2 若標的資產價格St遵循(1),則該亞式期權的Vf(t,S,J)價格為 (9) 其中,函數Φ(x)是標準正態分布的累積概率函數,J為路徑變量,且 證明 令 x=lnS, (10) V=U(x,y,t). 有偏微分: (11) 將(11)帶入(3)(4),可得 (12) U(T)=(ex-ey)U0(x,y). (13) (14) (15) 求解微分方程(14)(15),得到 (16) 其中, h4=r(T-t)-h1, h6=r(T-t), 利用傅里葉逆變換,可得 (17) 其中, U0(μ,k)=(eμ-ek)+, (18) 最終由公式(10)(17)(18),定理2.2得證. 定理2.3 幾何平均亞式期權看漲-看跌平價關系式為 C(S,J,t)-P(S,J,t)= 證明 令 W(S,J,t)=C(S,J,t)-P(S,J,t), 在{0≤S<∞,0≤J<∞,0≤t≤T}上,W滿足: (19) 考慮Cauchy問題: (20) (21) W(x,y)=a(t)ex-b(t)ey. (22) 帶入(20)(21),經比較系數得 (23) 且有 (24) 求解(23)(24),得到 (25) 將(25)代入(22),并考慮(10),定理2.3得證. 基于次分數布朗運動模型,以具有浮動敲定價格的亞式期權為例,用數值模擬計算探究Hurst指數H對期權價格的影響. 已知t=0時,有幾何平均亞式看漲期權Vf(0,S,J). Vf(0,S,J)=S0Φ(-d1)-S0exp(ρ1-ρ2)Φ(-d2). 假設模型相應參數為T=0.5,r=0.05,σ=0.8,Hurst指數H分別為0.5、0.6、0.8、0.9時,次分數布朗運動下,具有浮動敲定價格的幾何平均亞式看漲期權的計算結果如表1所示,比較圖如圖1所示. 表1 r=0.05,H取不同值時幾何平均亞式看漲期權計算結果 圖1 H取不同值時幾何平均亞式看漲期權計算結果比較 T=0.5,H=0.7,σ=0.8,無風險利率r分別為0.02、0.04、0.06、0.08時,次分數布朗運動下,具有浮動敲定價格的幾何平均亞式看漲期權的計算結果如表2所示,比較圖如圖2所示. 圖2 r取不同值時幾何平均亞式看漲期權計算結果比較 表2 H=0.7, r取不同值時幾何平均亞式看漲期權計算結果 由表1和圖1可知,H固定時,隨著股票價格S0增加,期權價格V逐漸增加;S0固定時,隨著H增加,期權價格V逐漸減小. 由表2和圖2可知,r固定時,隨著股票價格S0增加,期權價格V逐漸增加;S0固定時,隨著r增加,期權價格V也逐漸增加. 比較圖1和圖2可發現,從整體趨勢來看,期權價格V受Hurst指數H的影響相對來說較大,受無風險利率r的影響相對來說較小. 求得期權的顯示表達式是研究期權定價問題非常重要的一步.本文運用傅里葉變換方法給出了具有浮動敲定價格的幾何平均亞式期權顯示表達式,進而探究了次分數布朗運動機制下具有浮動敲定價格的幾何平均亞式期權定價問題.通過數值計算結果發現,Hurst指數和無風險利率固定時,股票初始價格與該期權價格呈正比;股票初始價格固定時,Hurst指數與該期權價格呈反比,無風險利率與該期權價格呈正比.
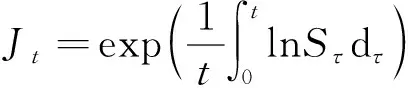
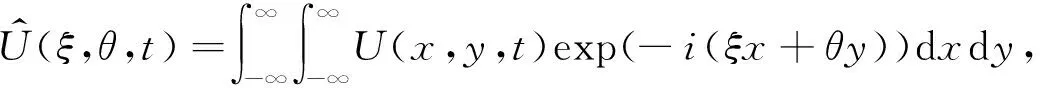
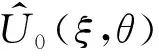

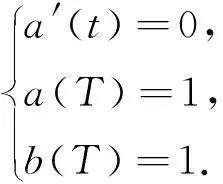
3 數值計算
4 結語

