基于PSO-BP的混凝土配比設(shè)計的仿真研究

劉 清

(閩南理工學(xué)院土木工程學(xué)院，福建 石獅 362700)

0 引言

混凝土配比的設(shè)計就是找尋適當(dāng)比例的水泥、骨料、水、外加劑等組成成分，得到符合要求性能的混凝土，并且盡可能地降低成本[1]。普通混凝土的傳統(tǒng)配比設(shè)計方法是計算-適配法，或基于逐級填充原理，或假定容量法和絕對體積法，將制成的混凝土試驗標(biāo)本養(yǎng)護到28天，測試其相關(guān)性能[2]。對于高性能混凝土，國內(nèi)外提出了很多方法。其中，法國路橋中心對高性能混凝土配比設(shè)計的研究比較先進[3]，其主要思想是在模型材料上用膠結(jié)漿體進行大量的流變試驗，并用砂漿進行力學(xué)實驗，避免了用直接的方法優(yōu)化配比參數(shù)時進行的大量試配工作。混凝土配比的設(shè)計方法不僅可以參照普通混凝土的設(shè)計方法，也可針對原材料的特點需要進行特殊的配比設(shè)計，例如再生混凝土的再生骨料預(yù)吸收法[4]。但一般都是依靠人為的經(jīng)驗來決定混凝土產(chǎn)制的和易性、隱蔽性和安全性這三大特性[5]，導(dǎo)致混凝土的質(zhì)量和性能不夠穩(wěn)定，而且生產(chǎn)上的隨意更改會引起管理上的混亂，造成對成品無法控制。本文以混凝土28天抗壓強度作為衡量混凝土性能的一項重要參數(shù)，采用粒子群算法加神經(jīng)網(wǎng)絡(luò)來建立混凝土強度與配比之間的關(guān)系模型，提高混凝土攪拌站配料的精度，以此來提高成品混凝土的質(zhì)量和性能，同時達到降低生產(chǎn)成本的目的。

1 BP神經(jīng)網(wǎng)絡(luò)模型概述

1.1 BP神經(jīng)網(wǎng)絡(luò)原理

BP神經(jīng)網(wǎng)絡(luò)是目前應(yīng)用最廣泛的神經(jīng)網(wǎng)絡(luò)模型之一，是1986年以Rumelhart和McCelland為首的科學(xué)家提出的一種按照誤差逆?zhèn)鞑ニ惴ㄓ?xùn)練的多層前饋網(wǎng)絡(luò)。BP神經(jīng)網(wǎng)絡(luò)模型包括輸入層(input layer)、隱層(hidden layer)和輸出層(output layer)。在進行神經(jīng)網(wǎng)絡(luò)訓(xùn)練前，需要對網(wǎng)絡(luò)的輸入、輸出參數(shù)進行歸一化處理。歸一化處理公式如下：

(1)

(2)

對樣本數(shù)據(jù)進行歸一化處理，可以減輕人工神經(jīng)網(wǎng)絡(luò)的訓(xùn)練難度，還可以讓那些比較大的數(shù)據(jù)仍然落在神經(jīng)元轉(zhuǎn)換梯度大的地方。根據(jù)樣本數(shù)據(jù)建立網(wǎng)絡(luò)模型，確定神經(jīng)網(wǎng)絡(luò)的輸入輸出參數(shù)和隱層單元數(shù)。

1.2 PSO優(yōu)化神經(jīng)網(wǎng)絡(luò)

粒子群算法(Particle Swarm Optimization，PSO)是一種并行算法，由KENNEDY J和EBERHART R C等開發(fā)出的一種優(yōu)化算法[6]。將BP網(wǎng)絡(luò)神經(jīng)元之間的所有權(quán)閾值編碼成實數(shù)向量，按照粒子群算法進行迭代，每次迭代過后將向量還原為權(quán)閾值，在進行所有樣本的訓(xùn)練，計算均方差。自行設(shè)定系統(tǒng)允許的最大誤差，如果迭代過后的均方差小于預(yù)設(shè)值，則計算結(jié)束，輸出結(jié)果，否則繼續(xù)迭代，直到迭代次數(shù)達到設(shè)定的最大值。

1.2.1 基本原理

BP神經(jīng)網(wǎng)絡(luò)的激活函數(shù)采用Sigmoid函數(shù)，然后用PSO算法搜索出最佳位置，使如下均方差指標(biāo)達到最小：

(3)

其中，N為樣本個數(shù)；c為神經(jīng)網(wǎng)絡(luò)輸出的個數(shù)；tk,p為第p個樣本的第k個理想輸出值；Yk,p為第p個樣本的第k個實際輸出值。

1.2.2 實現(xiàn)步驟

步驟一，確定網(wǎng)絡(luò)允許的最大誤差、最大迭代次數(shù)、最大速度、搜索范圍、確定粒子數(shù)。步驟二，根據(jù)粒子群規(guī)模，隨機產(chǎn)生一定數(shù)目的個體Xi以及其速度Vi。不同的個體代表神經(jīng)網(wǎng)絡(luò)的一組不同混凝土配比值。步驟三，根據(jù)適應(yīng)度函數(shù)計算每個粒子的優(yōu)劣程度。步驟四，比較適應(yīng)度，找到每個粒子的局部最優(yōu)值和各代粒子的所有的最優(yōu)值。步驟五，檢驗是否達到結(jié)束要求，若滿足則輸出混凝土配比，若不滿足則繼續(xù)迭代出下一組混凝土配比值，直到達到要求。

1.3 數(shù)據(jù)來源

現(xiàn)有數(shù)據(jù)是混凝土各自組成成分的用量以及對應(yīng)的28天抗壓強度值，見表1。本數(shù)據(jù)來自史峰和王輝的《MATLAB智能算法30個案例分析》[7]，其中，1～9組數(shù)據(jù)為訓(xùn)練集，用于建立神經(jīng)網(wǎng)絡(luò)模型；10～19組為測試集，用于測試模型的預(yù)測能力。

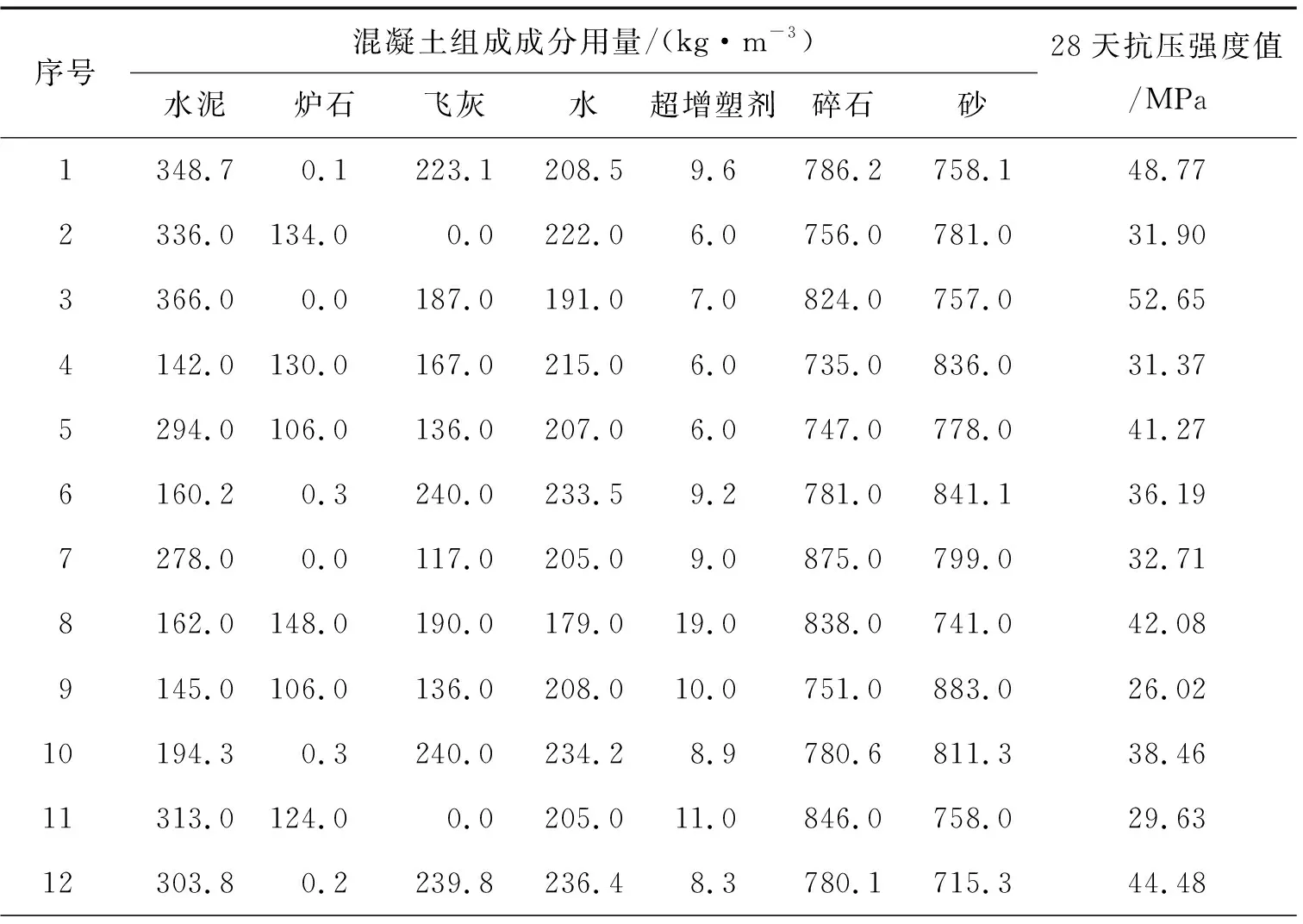
表1 混凝土組成成分用量原始數(shù)據(jù)

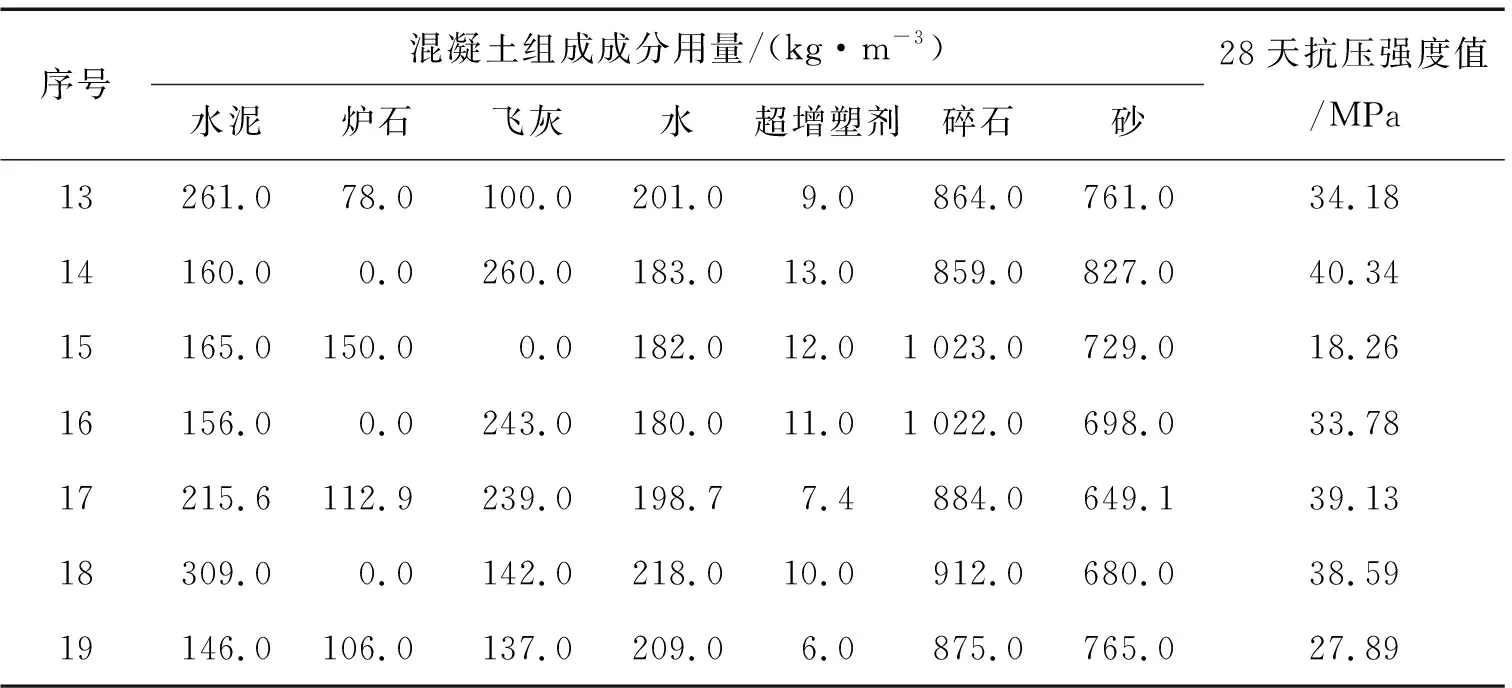
續(xù)表

根據(jù)表1，設(shè)定神經(jīng)網(wǎng)絡(luò)的輸入為混凝土各配料的量，所以輸入層單元數(shù)為7，輸出為混凝土28天抗壓強度值，即輸出層單元數(shù)為1。隱層單元數(shù)沒有精確的推導(dǎo)公式，但是可以用以下經(jīng)驗公式作為參考：

(4)

其中，n1為隱層單元數(shù)，n為輸入神經(jīng)元的個數(shù)，m為輸出神經(jīng)元的個數(shù)，a為在0～10之間的常數(shù)。

一般來說，隱層單元數(shù)比輸入神經(jīng)元個數(shù)要多，取隱層單元數(shù)為10。其他參數(shù)自行取值，但不可超出其參數(shù)的取值范圍，最終的神經(jīng)網(wǎng)絡(luò)模型結(jié)構(gòu)為7×10×1。

2 結(jié)果與討論

2.1 BP神經(jīng)網(wǎng)絡(luò)測試

將表1的數(shù)據(jù)輸入到BP神經(jīng)網(wǎng)絡(luò)模型中，得到每組數(shù)據(jù)的仿真結(jié)果，如圖1所示。

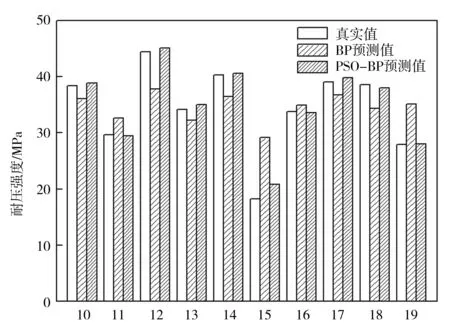
樣品編號 圖1 BP和PSO-BP神經(jīng)網(wǎng)絡(luò)測試結(jié)果

從圖1可以看出，此神經(jīng)網(wǎng)絡(luò)對測試樣本的仿真值與真實值存在相當(dāng)大的誤差。均方誤差MSE的數(shù)值越小越好；另一個描述誤差的數(shù)值R2，越接近于1表示模型越準(zhǔn)確。由研究結(jié)果得到MSE為0.059 042，R2為0.758 22，說明并不能準(zhǔn)確地描述出輸入與輸出的關(guān)系。這說明，這樣訓(xùn)練出來的BP神經(jīng)網(wǎng)絡(luò)中的權(quán)閾值并不是最優(yōu)的，需要用優(yōu)化算法進行權(quán)閾值優(yōu)化。因此，設(shè)置粒子群算法參數(shù)，迭代次數(shù)50次，種群規(guī)模20，粒子維數(shù)7，學(xué)習(xí)因子c1=1.914 45，c2=0.914 45。優(yōu)化完成后繼續(xù)用表1的測試樣本進行測試，測試結(jié)果如圖1所示，可見用粒子群算法優(yōu)化網(wǎng)絡(luò)權(quán)閾值得到的神經(jīng)網(wǎng)絡(luò)模型明顯比單純BP網(wǎng)絡(luò)模型效果更好。PSO+BP神經(jīng)網(wǎng)絡(luò)模型的均方誤差MSE已經(jīng)降到0.001 550 8，R2為0.992 09。根據(jù)PSO+BP神經(jīng)網(wǎng)絡(luò)模型，可以設(shè)計出已知強度條件下的混凝土配比值。用PSO+BP神經(jīng)網(wǎng)絡(luò)模型描述混凝土強度與各自材料用量的關(guān)系，具有很強的可靠性和適應(yīng)性。

2.2 最佳混凝土配比

利用粒子群算法迭代尋優(yōu)，設(shè)置最終得到的混凝土28天抗壓強度值為35，迭代次數(shù)為100。使用PSO-BP神經(jīng)網(wǎng)絡(luò)進行迭代運算，得到如圖2所示的誤差變化圖。

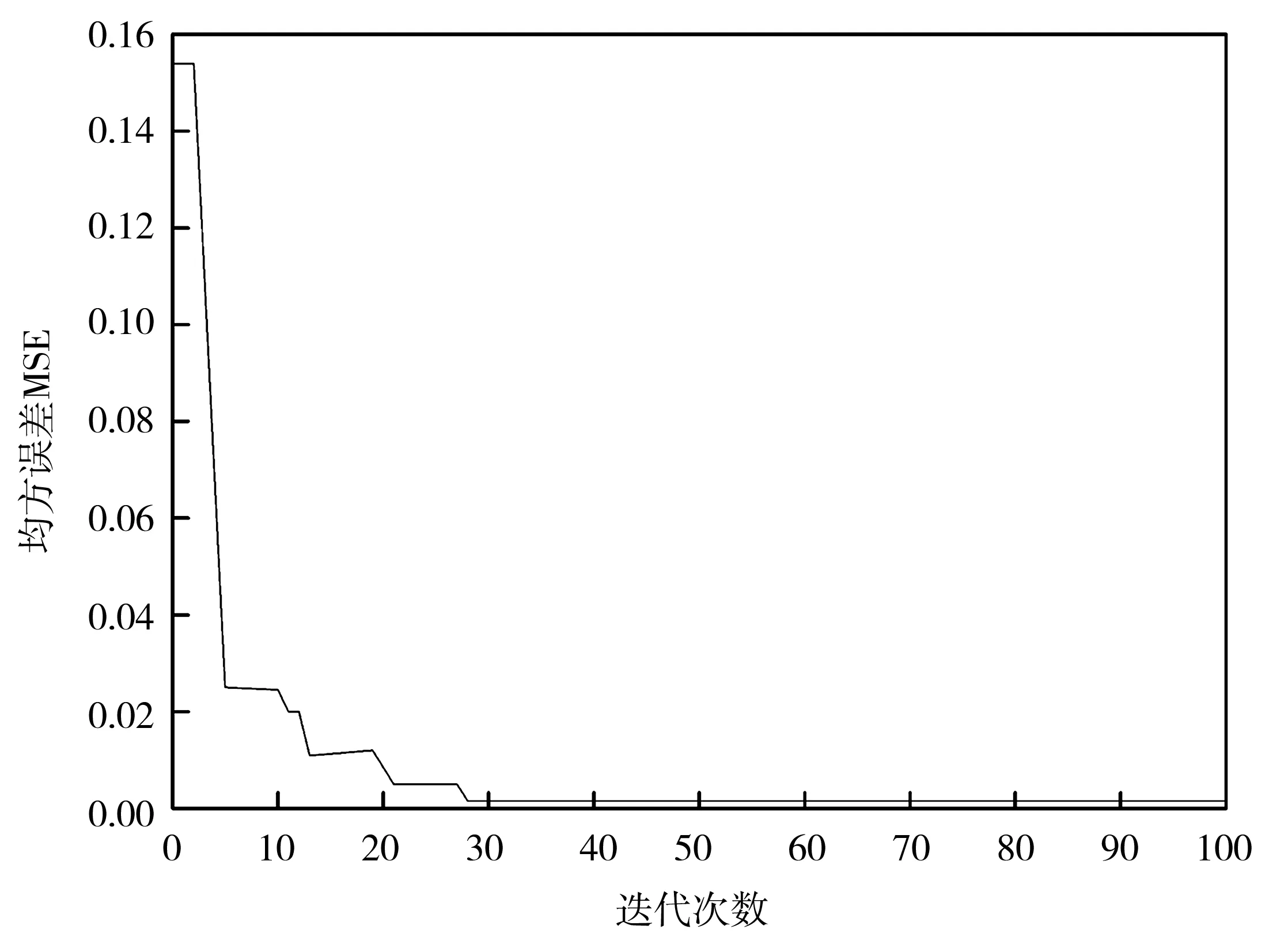
圖2 配比迭代后的仿真誤差曲線

從圖2可以看出，這種方法收斂速度快，當(dāng)?shù)降?7次左右，誤差就降到一個很低的水平了。除此之外，精度也很高，誤差保持在0.000 1的范圍內(nèi)，因此，通過這種方法可以有效地設(shè)計配比值。最終混凝土最佳配比分別為：水泥293.737 kg/m3，爐石0，飛灰93.683 kg/m3，水234.399 kg/m3，超增塑劑19 kg/m3，碎石1 037.664 4 kg/m3，砂640.9 kg/m3。

2.3 混凝土成本篩選

混凝土生產(chǎn)配比的選擇需要考慮眾多因素，例如，當(dāng)固定28天混凝土抗壓強度值時，所對應(yīng)的混凝土配比值不是固定的，理論上來說有無數(shù)種，運行一次程序，就得到一種混凝土配比值。在這些配比值當(dāng)中該如何取舍，需要考慮的是成本問題。在得到的有限配比值中肯定有一組是最經(jīng)濟的，通過計算每一組配比值得出混凝土的成本，篩選出成本最低的一組作為最佳配比。計算成本時不包括運費、員工工資等外部因素，只計算混凝土本身各種材料的費用總和。由于配比設(shè)計中只包含主要成分，因此可以用單位重量混凝土所需的價格比較不同配比混凝土的性價比。設(shè)混凝土生產(chǎn)配比值為x1,x2,…,xn，單位是kg/m3，每種材料的價格是a1,a2,…，an,單位為元/kg。因此，可以計算出成本Y(元/kg)為

(5)

設(shè)定混凝土28天抗壓強度值為35，得到10組混凝土生產(chǎn)配比值。每組配比結(jié)果如表2所示。

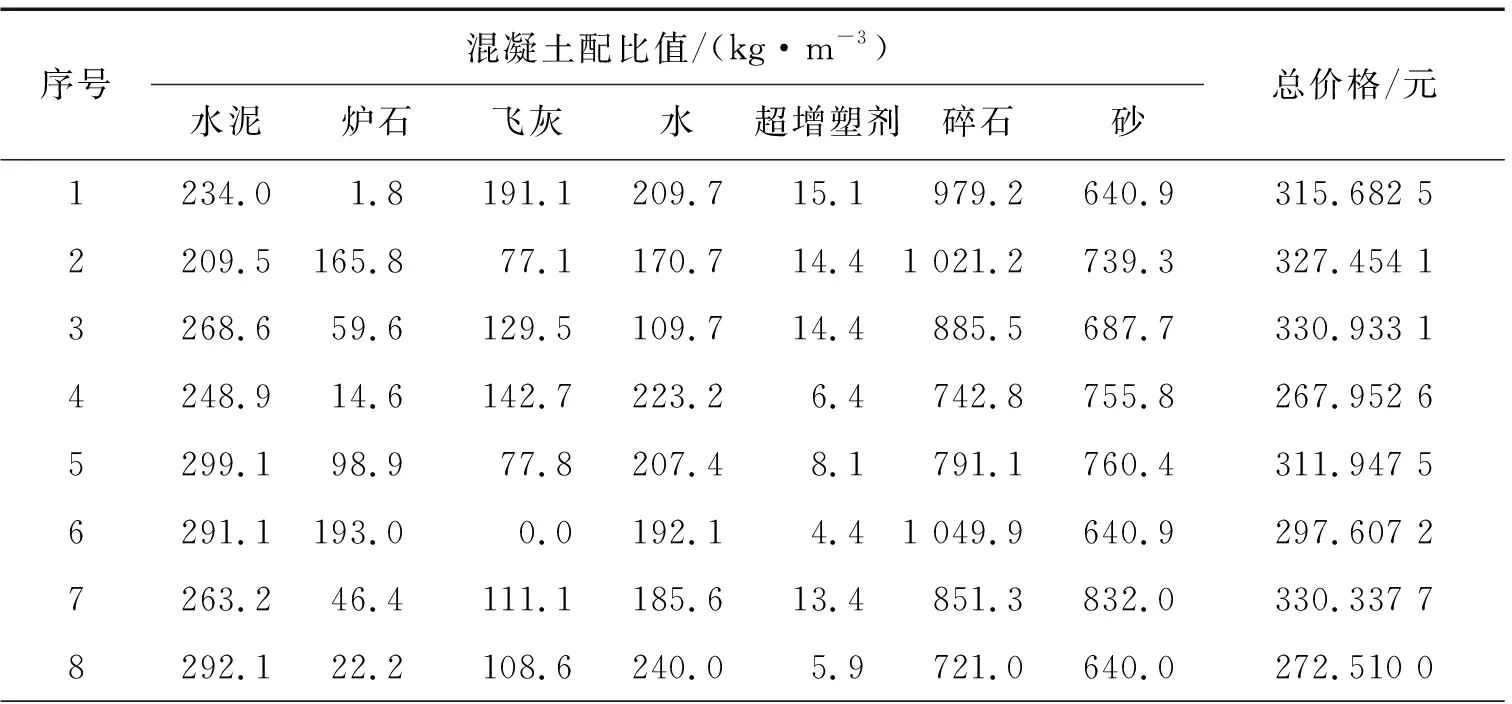
表2 10組28天抗壓強度值為35的混凝土配比值

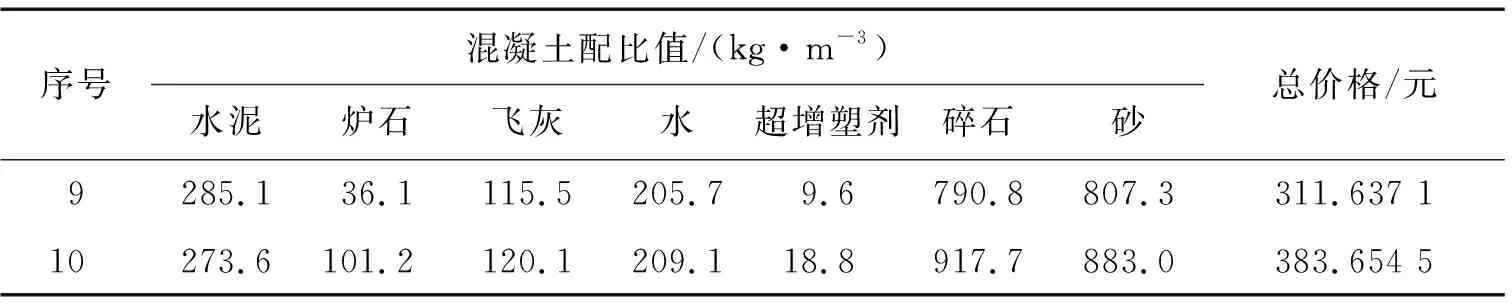
續(xù)表

對于這些不同種類的混凝土不同配比值，計算每組的成本總和。2021年市場上每種混凝土組成材料的平均價格分別為：水泥是0.46 元/kg，爐石0.15 元/kg，飛灰0.07 元/kg，水0.002 8 元/kg，超增塑劑5.9 元/kg，碎石0.05元/kg，砂0.087 元/kg。由表2可以看出第4組混凝土的價格最低，因此選取第4組混凝土生產(chǎn)配比，即水泥用量248.9 kg/m3，爐石14.6 kg/m3，飛灰142.7 kg/m3，水223.2 kg/m3，超增塑劑 6.4 kg/m3，碎石 742.8 kg/m3，砂 755.8 kg/m3。混凝土生產(chǎn)配比的仿真設(shè)計，可以不進行實際操作而節(jié)約時間和成本，事先設(shè)計好最理想生產(chǎn)配比，直接應(yīng)用到混凝土攪拌站中即可。

3 結(jié)語

本文提出的粒子群算法結(jié)合BP神經(jīng)網(wǎng)絡(luò)的方法能夠很好地解決混凝土配比的設(shè)計問題。從計算機仿真結(jié)果可以看出，利用粒子群算法優(yōu)化權(quán)閾值后的神經(jīng)網(wǎng)絡(luò)能夠很好地描述混凝土各組成的用量與最終成品的強度之間的關(guān)系。由此神經(jīng)網(wǎng)絡(luò)模型就可以繼續(xù)通過粒子群算法進行特定目標(biāo)值的輸入搜索，最終得到數(shù)組能夠達到要求的混凝土配比。如果需要可再根據(jù)其他要求從其中篩選更適合的方案。這種方法不僅能設(shè)計混凝土生產(chǎn)配比，還能粗略地判斷出混凝土強度的上下限，避免設(shè)計要求的不合理性。但是這樣的設(shè)計只是理論上的計算，并不是絕對準(zhǔn)確的，應(yīng)用到實際生產(chǎn)過程中可能會造成誤差，這時需要對設(shè)計好的混凝土生產(chǎn)配比進行微調(diào)，直到滿足需求。