有關中點基本圖形的分類及輔助線的加法
武漢市光谷實驗中學 劉姜濤 康柳燕
1 引言
中點問題在中學階段的地位舉足輕重,與中點密切相關的線段[1]主要有兩種:中位線和中線.這兩個知識點貫穿整個初中幾何,題目難度往往較大,學生解題沒有方向.為此,筆者總結了7類有關中點的基本圖形及做題方法,以供參考.
2 有關中點的基本圖形的分類及解法
7類有關中點的基本圖形及做題方法總結如表1:

表1
中位線一般出現在三角形和四邊形的圖形中,中線則在三角形的題型中經常使用,所以無論是分析圖形還是構造輔助線,這兩種線段都是我們的重要解題工具.下面展示這兩者在具體圖形中的妙用.
2.1 角分線+垂直→中位線
圖中出現角平分線和一個直角,可以考慮構造等腰三角形,利用等腰三角形三線合一的性質得到中點,再連接其它中點得中位線.
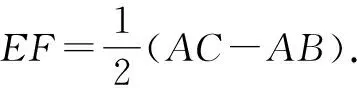
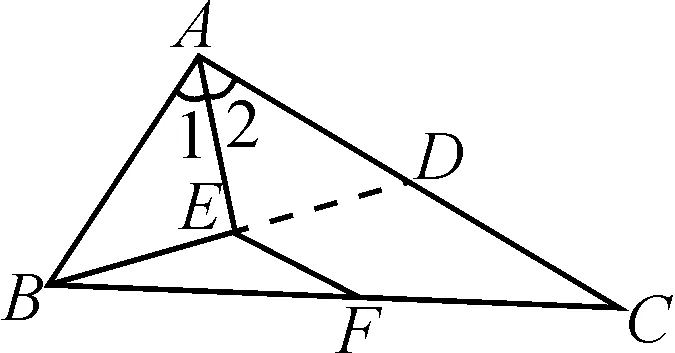
圖1
略證:延長BE交AC于點D.
AB=AD,BE=DE(三線合一),
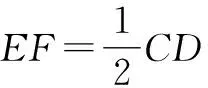
2.2 動點問題中的中位線
在變化中尋找不變是動點問題的基本思路,要確定動點的軌跡關鍵是找到不變的重要點、起點、終點,其中中點是常用解題工具[2].
基本圖形2:如圖2,已知P為線段AB上的動點,以AP,BP為邊在AB同側作等邊三角形ACP和等邊三角形PDB,G為CD中點.求當點P從點A運動到點B時,點G移動路徑的長.
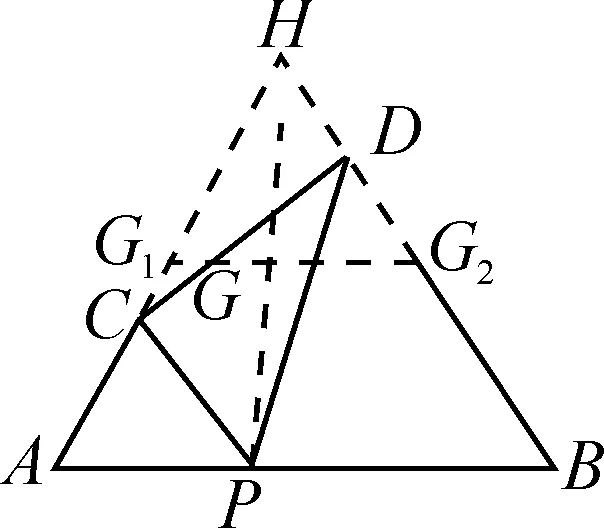
圖2
略解:延長AC,BD交于點H.
當點P在點A時,CD=AH;當點P在點B時,CD=BH.
∵四邊形CHDP是平行四邊形,
∴CD與PH互相平分.
∴點G為PH中點.
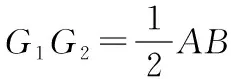
2.3 三角形中的1個中點
三角形中出現中點,作中位線是常用的輔助線作法之一.
基本圖形3:已知點D為線段AB的中點,DE平分△ABC的周長,求線段DE的長度.
方法1提示:如圖3,取三角形另一邊的中點,連接兩個中點構造中位線.
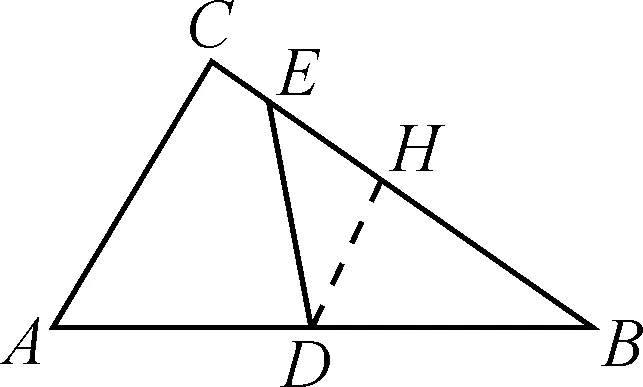
圖3
略解:在BC上取中點H,連DH.
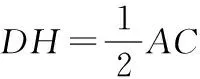
根據△EHD中的線段關系求DE.
方法2提示:如圖4,將已有線段視作中位線,構造新的三角形.
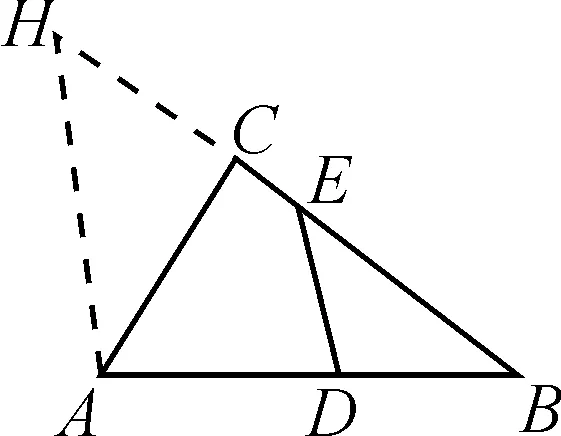
圖4
略解:倍長BE至點H,連AH.
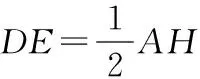
求出AH的長度(三角形線段關系).
2.4四邊形中的2個中點
除了三角形,在四邊形中也經常需要用到中位線這種輔助線,解題時需要利用中位線進行線段關系的轉化.
基本圖形4:如圖5,已知E為AB的中點,F為CD的中點,尋求EF與AC,BD的關系.

圖5
提示:取另一邊的中點,分別連接得到兩條中位線.
略解:在BC上取中點H,連接HE,HF.


基本圖形5:如圖6,已知E為AB的中點,點F為CD的中點,尋求EF與AD,BC的關系.

圖6
提示:在對角線上取中點.
略解:連AC,取AC的中點H,連EH,FH.

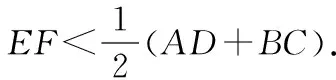
2.5四邊形中的4個中點
若四邊形中出現多個中點時,將中點連接形成的線段集中在一個三角形中考慮.
基本圖形6:如圖7,已知點E,F,G,H分別為AB,BC,CD,DA的中點,求證:四邊形EFGH為平行四邊形.

圖7
略證:連AC(或BD) .
由HG(中位線) ,
得HG∥EF,HG=EF.
因此,四邊形EFGH為平行四邊形.
2.6共斜邊的直角三角形
中點出現在直角三角形的斜邊上時,要注意運用“直角三角形斜邊上的中線等于斜邊的一半”這一性質.
基本圖形7:如圖8,已知AC⊥AB,DC⊥BD,H為BC的中點,求證:∠AHD=2∠ABD.
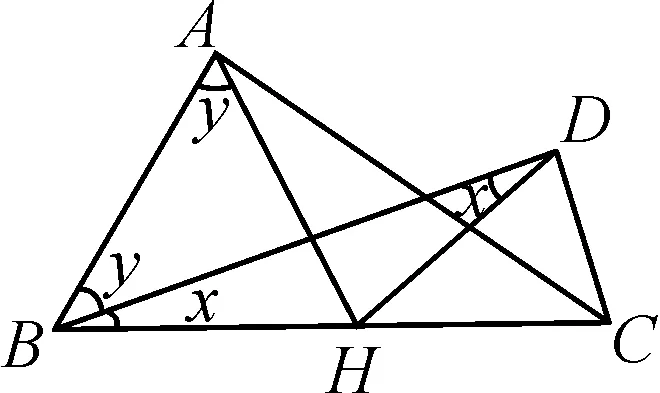
圖8
提示:公共斜邊取中點.
略證:AH=BH=CH=DH.
∠ABD=y-x,
∠AHD=∠AHC-∠DHC=2y-2x
=2(y-x)=2∠ABD.
基本圖形8:如圖9,已知AC⊥AB,DC⊥BD,H為BC的中點,求證:∠AHD=2∠ABD.
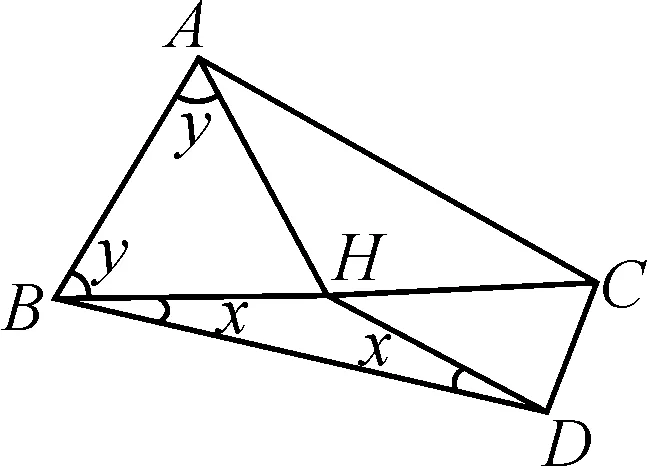
圖9
提示:公共斜邊取中點.
略證:AH=BH=CH=DH.
∠ABD=x+y,
∠AHD=∠AHC+∠DHC=2x+2y
=2(x+y)=2∠ABD.
2.7 “T”字形
若復雜圖形中有一條線段AB及過AB中點C的另一條線段DC,且滿足AC=BC=DC,對于這樣的“T”字形,常考慮利用中位線,反過來構造三角形.
基本圖形9:如圖10,C為AB的中點,連接端點A,D并倍長,構造出以CD為中位線的三角形;

圖10
或者如圖11,連接端點B,D并倍長,構造出以CD為中位線的三角形;
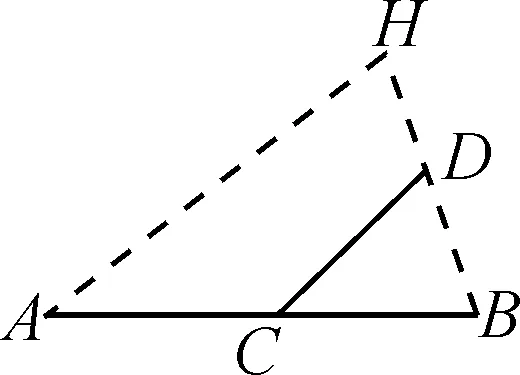
圖11
或者如圖12,以AB為直角三角形的斜邊構造出直角三角形ADB.
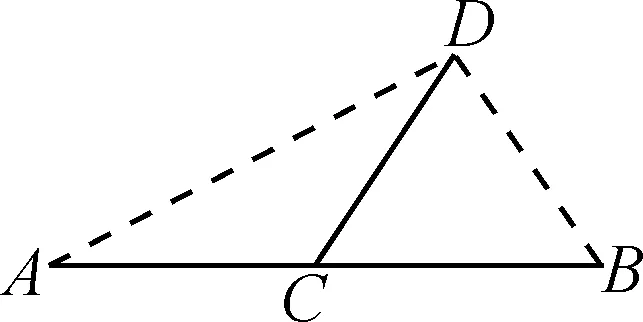
圖12
3 應用舉例


圖13
略證:如圖14,連DN并延長交AC于點H,連BH.

圖14
在△EDN和△CHN中,

∴△EDN≌△CHN(ASA).
∴ED=EA=CH.
易證△CAE≌△BCH(SAS),
∴CE=BH=2MN.
對于例題,還可以用下面三種方法添加輔助線,如圖15~17,證明思路與上面類似從略.
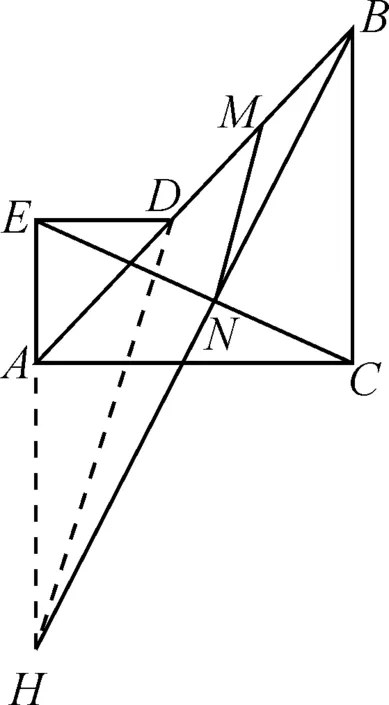
圖15

圖16
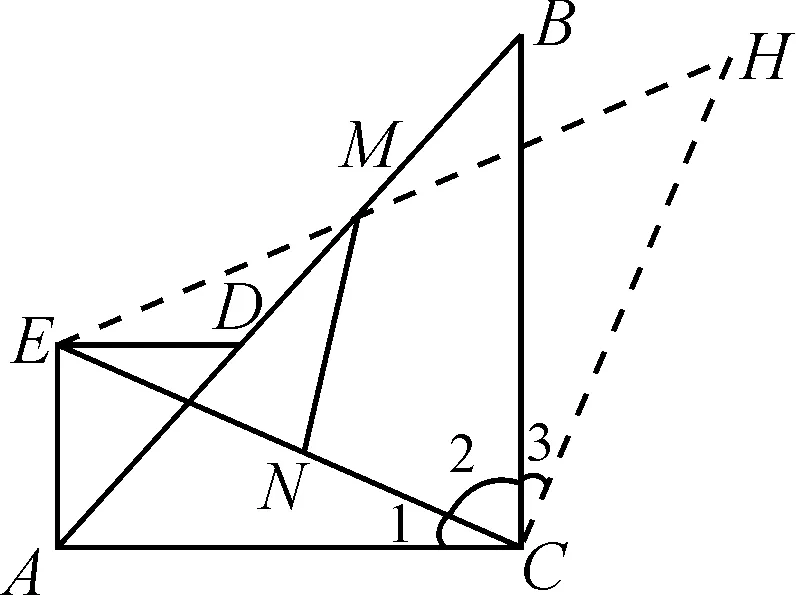
圖17
4 結束語
本文中給出了7類有關中點基本圖形的分類及輔助線的加法及應用.中點問題看似復雜多變,實則掌握了基本圖形及其對應解法,便可逐一攻克,讓中點問題不再困難.

