零碳園區電-氫混合儲能系統多目標優化配置

張馳,周駿,趙鑌,李嘉樂,楊博

(1.云南電網有限責任公司昆明供電局，昆明市 654100；2.昆明理工大學電力工程學院,昆明市 650500)

0 引 言

隨著社會科技的不斷發展與進步，以化石燃料為基礎的傳統能源已難以滿足人類社會的需求，并正在加劇環境污染和全球變暖[1]。目前能源和環境問題已經成為社會可持續發展面臨的兩個嚴峻挑戰。因此，減小碳排放并大力發展清潔能源已成為可持續發展不可或缺的手段[2-3]。

儲能系統(energy storage systems,ESSs)憑借其削峰填谷和靈活的能量管理能力，可有效解決“零碳”園區棄風棄光、電壓越限、潮流反向等問題[4-6]。氫能因其清潔性和可持續性而被譽為21世紀的終極常規能源。氫氣儲能系統(hydrogen energy storage systems,HESSs)利用富余的電能制氫，并將其儲存起來或供下游產業使用；當負荷增大時，儲存的氫氣可利用燃料電池(fuel cell,FC)進行發電回饋電網，此過程清潔高效、生產靈活。因此，合理配置HESSs對推進可持續發展理念，漸進實現“零碳”園區/低碳城市的戰略規劃目標起著至關重要的作用。

近年來，國內外學者對ESSs的規劃進行了大量研究[7-11]。然而大多數研究模型為單目標模型，其存在無法合理地協調儲能的經濟性與電網穩定性等問題。文獻[12-14]分別以年凈收益最大、年綜合成本最小以及全生命周期損耗成本(life cycle cost,LCC)最小為優化目標，建立了單目標電池儲能系統(battery energy storage systems,BESSs)規劃模型。文獻[15]以電網損耗為目標函數對BESSs接入的位置和容量進行規劃，以減少配電網功率損耗。文獻[16]以投資運維費用最小為目標，建立BESSs規劃-運行兩階段隨機優化模型，然而該模型并未考慮BESSs接入后對電網穩定性的影響。上述研究模型均為單目標規劃模型，其沒有考慮ESSs規劃與電網運行條件之間的耦合問題。因此，搭建ESSs多目標優化配置模型，不僅可以充分挖掘ESSs的潛力，而且可以在ESSs經濟效益和電網穩定之間實現更優的平衡。

為此，研究者通過線性加權將ESSs規劃的多個優化目標加權為單個目標進行優化求解[17]，然而該方法求解的規劃方案過于依賴于決策者的主觀意識，難以客觀地分配每個目標的權重。文獻[18]提出了一種考慮新能源與負荷不確定性的雙層BESSs規劃方案，然而其并未提及Pareto非支配解的篩選方案，且沒有考慮接入ESSs后對電網穩定性的影響。文獻[19]以節點電壓波動、負荷波動以及ESSs總容量最小建立多目標優化模型，但該模型并未考慮ESSs的投資運維等成本，缺乏實際工程應用性。文獻[20]以ESSs經濟效益與電壓質量為優化目標，建立多目標優化配置模型。但電壓質量并不能完全體現接入ESSs后電網真實的運行狀況。目前已發表的ESSs規劃研究中較少涉及HESSs，但隨著國家對“雙碳”戰略的推進，為確保我國經濟在“零碳經濟”時代處于領先地位，改變能源結構至關重要。因此，探索氫能產業鏈，大力發展HESSs，構建“零碳”園區已成為可持續發展的重要道路。

基于上述討論，本文基于帶精英策略的非支配排序遺傳算法(non-dominated sorting genetic algorithm-II,NSGA2)，在新能源高滲透環境下對電-氫儲能進行協同優化配置，并以最小LCC、系統網損、聯絡線功率偏差、負荷波動和電壓波動為目標建立多目標優化模型，主要內容如下：

1)建立基于Pareto的多目標優化模型，基于5個目標建立BESSs和HESSs的多目標規劃最優選址配容模型。

2)采用聚類算法對全年的負荷、風、光出力曲線進行典型日聚類，基于其時序特性組合得到4種典型場景。在不同典型場景下分別進行仿真計算，得到各個目標函數在全年的總和。

3)基于擴展的IEEE-33節點系統進行仿真測試，通過與多目標浮游算法(multi-objective mayfly algorithm,MOMA)進行對比，驗證NSGA2算法尋優特性。

1 BESSs/HESSs配置模型

本文主要研究在供需雙方均不確定的情況下，HESSs和BESSs與新能源發電聯合構成的風、光、電-氫儲“零碳”園區協調調度的問題。該調度框架由“零碳”園區、BESSs、光伏發電、風力發電、電解槽、FC單元以及儲氫罐(hydrogen tank,HT)所構成。

BESSs、HESSs、光伏、風電等分布式電源接入示意如圖1所示。控制中心通過及時監測電網運行狀態，控制儲能的充放電運行，實現儲能單元與電網之間的能量交換。BESSs任何時間的荷電狀態(state of charge,SOC)是充放電運行的重要參數，它由容量、充放電功率、充放電效率等變量來描述。BESSs的SOC計算如下：

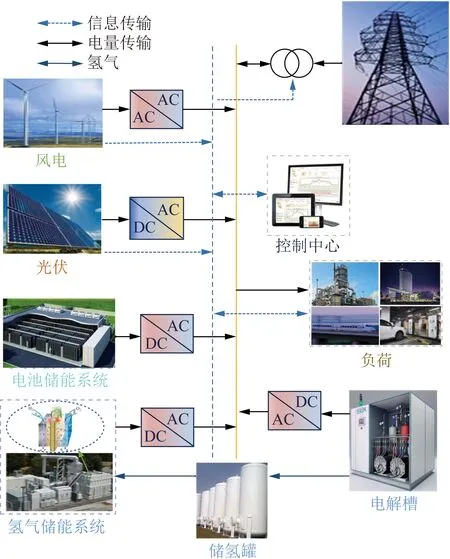
圖1 與電網直連的電池儲能和氫氣儲能系統模型Fig.1 Typical configuration of BESSs and HESSs directly connected to power grid

(1)

式中：Si(t)為節點i電池儲能系統t時刻的SOC；Pcha,i(t)和Pdis,i(t)為t時刻節點i的充放電功率；ηcha,i和ηdis,i為t時刻節點i的充放電效率；Δt為調度周期。

BESSs與電網之間的交換功率可以表示為:

Pgrid,i(t)=Pcha,i(t)-Pdis,i(t)

(2)

由于充放電不能同時進行，故BESSs與電網之間的功率交換必須滿足式(3)：

Pcha,i(t)·Pdis,i(t)=0

(3)

1.1 BESSs/HESSs選址定容規劃

ESSs的選址定容是一個高維度、多目標、復雜約束條件下的問題。以“零碳”園區電-氫混合儲能的LCC、園區每日的線路功率損耗、聯絡線交換功率偏差、電壓波動和負荷波動最小為目標，建立基于Pareto原理的多目標優化模型，如下：

(4)

式中：F(x)由目標函數F1、F2、F3、F4、F5組成，分別為BESSs和HESSs的LCC、每日的網損、聯絡線交換功率波動、電壓波動與負荷波動；x表示由優化變量構成的決策空間，即BESSs和HESSs的最優布局、容量和每小時的功率；H(x)為模型需要滿足的約束條件。

1.2 目標函數

1.2.1 全生命周期損耗

LCC是評價ESSs經濟性的重要指標，它包含總投資成本(total capital cost,TCC)、維護成本(maintenance cost,MC)、運行成本(operation cost,OC)、更換成本(replacement cost,RC)、處置和回收成本(disposal and recycling cost,DRC)。HESSs與BESSs的LCC如下所示：

(5)

1)BESSs的投資成本:

(6)

式中：NBESS表示“零碳”園區內BESSs的安裝數量；cbat為單個電池的成本；cEPCD,B表示BESSs的施工、采購和建設(engineering,procurement and construction,EPC)成本及開發商成本；Isub,B是政府對BESSs的補貼；EBESS,i是第i臺BESS的容量；μCRF,B表示資本回收系數(capital recovery factor,CRF)。

2)BESSs的維護成本:

(7)

式中：cFMC,B表示單臺BESSs的年固定MC；PBESS,i是第i臺BESSs的功率。

3) BESSs的運行成本：

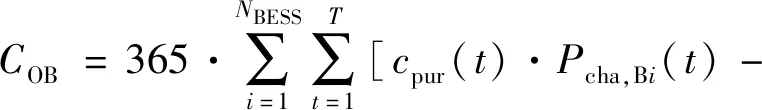
(8)

式中：T表示24個時段；cpur(t)和ccell(t)分別表示買入和賣出時的電價；Pcha,Bi和Pdis,Bi分別為第i臺BESS的充放電功率。

4) BESSs的更換成本：

(9)

式中：m和nB分別為電池的壽命和更換次數；α為電池的年成本損耗率；r表示折現率。

5) BESSs的處置和回收成本：

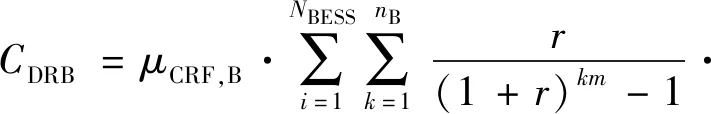
(10)

式中：γB是BESSs的回收效益。

6) HESSs的投資成本：

(11)

式中：μCRF,H是HESSs的成本回收系數；NHESS為HESSs的安裝數量；cFC和cE分別為FC和電解槽的成本；cHT和QHT,i為HT的成本和容量；PHESS,i是第i臺HESSs的功率大小；CEPCD,H表示HESSs的EPC成本，占總成本的20%；Isub,H表示政府對HESSs的補貼。

7) HESSs的維護成本：

(12)

式中：cFMC,H表示FC的年固定MC；PHESS,i為第i臺HESSs的功率。

8) HESSs的運行成本：

(13)

式中：Pcha,Hi(t)和Pdis,Hi(t)表示第i臺HESSs的充放電功率；QH,i表示HESSs一天內的氫氣總產量；qH為每kWh電的氫氣產量；IH2表示每kg氫氣的利潤，為氫氣的售價sH2減去氫氣生產成本cH2和運輸成本cD；PH,i為所產氫氣發電量；pH為每kg氫氣的發電量；μ和v為氫氣賣出量與用來發電的氫氣量占氫氣生產總量的比值。

9) HESSs的更換成本：

(14)

式中：nH為HESSs的更換次數；β為HESSs的年成本損耗率；M為HESS的壽命。

10) HESSs的處置和回收成本：

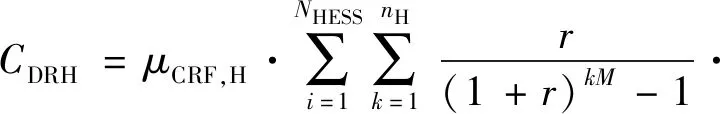
(15)

式中：γFC為FC的回收效益。

1.2.2 零碳園區的系統網損

BESSs和HESSs并網將改變“零碳”園區的潮流。本文在ESSs的選址定容規劃中考慮了電網的損耗，用每日的功率損耗表示，如下：

(16)

式中：L是“零碳”園區的聯絡線總數；Rj表示第j條聯絡線上的電阻；Ij(t)為t時刻第j條聯絡線上的電流。

1.2.3 零碳園區的聯絡線交換功率偏差

由于新能源出力的間歇性，當其并入電網時會產生較大的功率波動。本文在ESSs的選址定容規劃中考慮了電網的功率穩定性，用每日的聯絡線功率偏差表示，如下：

(17)

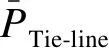
1.2.4 零碳園區的負荷波動

ESSs可對負荷波動進行平抑。本文在ESSs的選址定容規劃中同時考慮“零碳”園區的功率穩定性，用并網點每日功率波動表示，如下：

(18)

式中:Pload(t)、Ppv(t)和Pwind(t)分別為t時段內的系統負荷、光伏以及風電出力。

1.2.5 零碳園區的電壓波動

本文在ESSs的選址定容規劃中考慮了電網的電壓質量，用每日的電壓波動表示，如下：

(19)

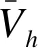
1.3 約束條件

1.3.1 等式約束

節點功率平衡約束:

(20)

式中:Ph(t)為t時刻節點h注入的有功功率；Qh(t)為t時刻節點h注入的無功功率；θhg(t)為t時刻節點h與g之間的電壓相角差；Vh(t)和Vg(t)分別表示t時刻節點h和節點g的電壓；Ghg和Bhg分別為節點h和g之間的線路電導和電納。

1.3.2 不等式約束

1) 節點電壓約束:

(21)

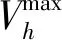
2) 并網點功率約束:

(22)

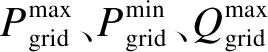
3) BESSs與HESSs容量與功率約束：

(23)

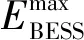
4) BESSs充放電約束：

(24)

式中：ηcha_B和ηdis_B分別為BESSs的充電效率和放電效率。

5) HESSs的充放電約束：

(25)

式中：ηcha_H和ηdis_H分別為HESSs的充放電效率。

6) SOC約束:

(26)

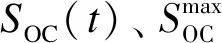
2 基于非支配排序遺傳算法的模型求解

2.1 非支配排序遺傳算法

本文采用尋優性能良好的NSGA2求解最優BESSs與HESSs選址定容規劃問題，并在算法內部調用Matpower工具箱采用快速解耦算法進行配電網潮流計算。NSGA2算法的具體內容如下[21]：

1)種群初始化。

2)基于Pareto對種群進行排序，確定支配種群與被支配種群。

3)根據函數適應度值的大小對同一非支配層中的個體的擁擠度進行計算，計算公式為：

(27)

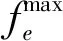
4)基于二進制競標賽隨機選擇兩個個體，Pareto等級高的個體進入下一個種群，等級相同選擇擁擠度更高的種群。

5)對種群采用模擬二進制交叉和多項式變異。

6)基于精英保留策略，將父代和子代種群混合組成新種群。

7)按Pareto等級由高到低依次將非支配集放入新的父代種群。

8)重復步驟5)—7)，獲得Pareto最優解集，NSGA2運用到電-氫儲能系統選址的流程如圖2所示。

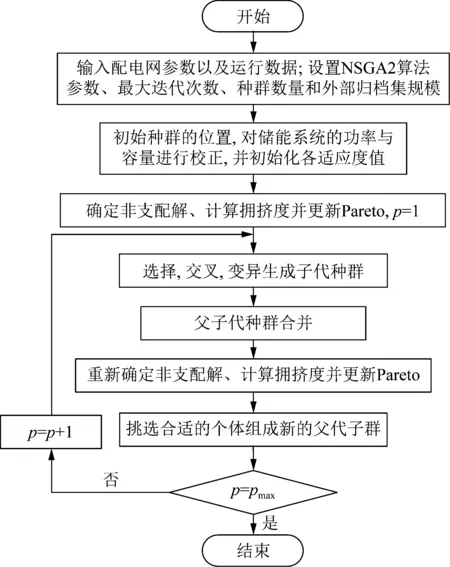
圖2 NSGA2算法用于電-氫儲能系統流程圖Fig.2 The flowchart diagram of the proposed NSGA2 used for electricity-hydrogen hybrid energy storage system

2.2 Pareto解集存儲與篩選

算法迭代過程中，采用外部歸檔集來存儲Pareto非支配解集。NSGA2在每次迭代中獲得的新非支配解集逐一與原非支配解集進行比較并更新外部歸檔集，具體流程如下[22]：

1)如果新解支配了歸檔集中的一組解，則將歸檔集中被支配的解替換為新解；

2)如果歸檔集中至少有一個解優于新解，那么新解將被舍棄;

3)如果新解與歸檔集所有的解互不支配，則將新解加入歸檔集。

歸檔集只能存儲有限數量的解，因此為了提高Pareto最優解集分布多樣性，選擇去除歸檔集中類似的非支配解，被刪除的解需要滿足以下方程：

(28)

2.3 基于熵權法的灰靶決策

本文設計了一種基于熵權法(entropy weight method,EWM)的灰靶決策方案，將Pareto非支配解集中的折中解作為最優決策方案。首先，依據各評價指標，建立樣本矩陣。其次，建立決策矩陣，并通過決策矩陣在由Pareto解集形成的灰色決策區域中選擇靶心。最后，通過EWM得到各解到靶心的距離。根據距離的排序結果可以得到最優決策解[23]。

1)建立樣本矩陣。

將所有解的歸一化適應度函數F作為評價指標之一，建立樣本矩陣。本文考慮在樣本矩陣中增加2個相關指標，一個是每個解與理想點之間的歐氏距離(Euclidean distance,ED)ED，另一個是每個解與平衡點之間的馬氏距離(Mahalanobis distance,MD)MD。因此，樣本矩陣表示為:

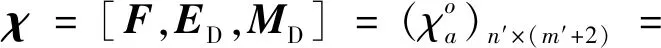
(29)

(30)

(31)

(32)

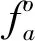
2)計算靶心。

采用算子qa對樣本矩陣進行無量綱化，其計算式如下：

(33)

基于算子qa與樣本矩陣建立決策矩陣V，如下:

(34)

3)建立權重與馬氏距離。

基于EWM可以客觀地獲得各評價指標的權重，并從Pareto非支配解集中篩選出最優折中解。權重ωa和熵值Ea計算如下：

(35)

(36)

(37)

每個解到靶心的MD可以表示為：

(38)

根據MD對非支配解進行排序。歸檔集中的每組解都被認為是一個獨立的決策方案。選取最接近靶心的解作為最優決策解。

3 場景聚類

考慮負荷、風電和光伏出力的不確定性，本文采用多個典型日場景下的負荷、風光曲線代表全年。首先，采用一種模糊核C-均值(fuzzy kernel C-means,FKCM)[24]聚類算法處理某園區的年歷史數據，如圖3所示。綜合考慮負荷、風電和光伏典型日曲線的相關性，通過場景組合得到4種聚類場景，每種場景的組合方式及對應天數如表1所示。

表1 組合場景聚類結果Table 1 Clustering results of composition scene

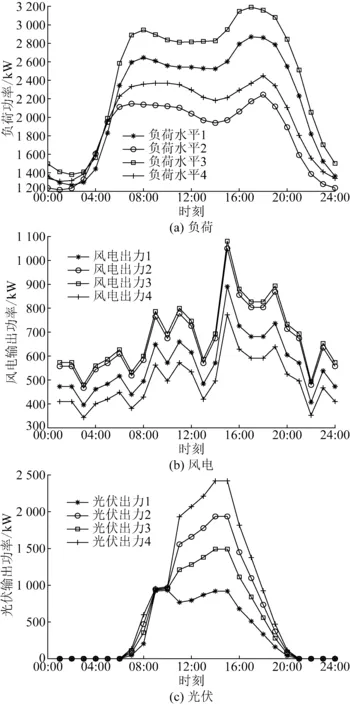
圖3 負荷、風電和光伏的典型日曲線Fig.3 Typical diurnal curves of load,wind and PV power

4 算例分析

4.1 仿真模型

本文采用擴展IEEE-33節點測試系統[25]進行仿真分析，以驗證所提方法接入ESSs的有效性，其拓撲結構如圖4所示，主要參數如表2所示。考慮高比例新能源的滲透，在節點7、11、17分別接入風電1、2、3，在節點32接入光伏1。仿真僅考慮新能源場站的有功輸出。為驗證所提NSGA2的優越性，仿真算例引入MOMA進行對比。兩種算法的基本參數設為一致，即最大迭代次數均設置為100；種群規模均設置為20；外部歸檔集規模設置為20。此外，表3和表4分別提供了ESSs的主要成本參數[26-29]和分時電價，其中持續放電(duration time,DT)時間越長電池成本越高。

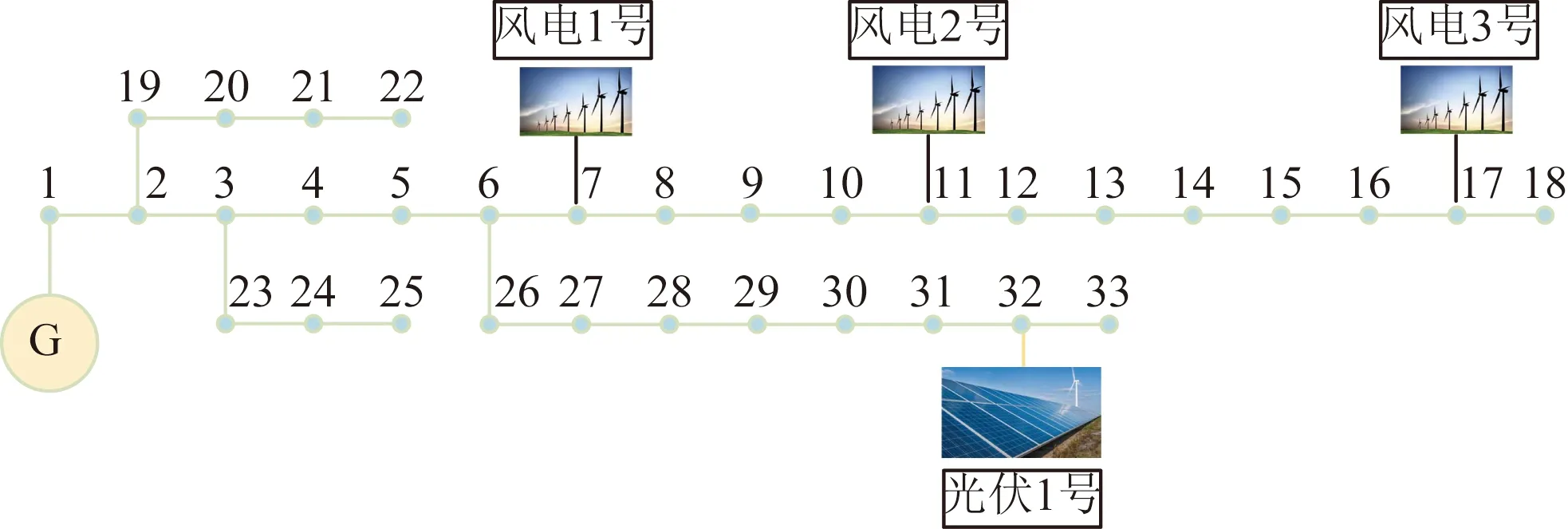
圖4 擴展的IEEE-33節點系統拓撲Fig.4 Topology of the extended IEEE 33-node system

表2 電網主要參數Table 2 Main parameters of power grid

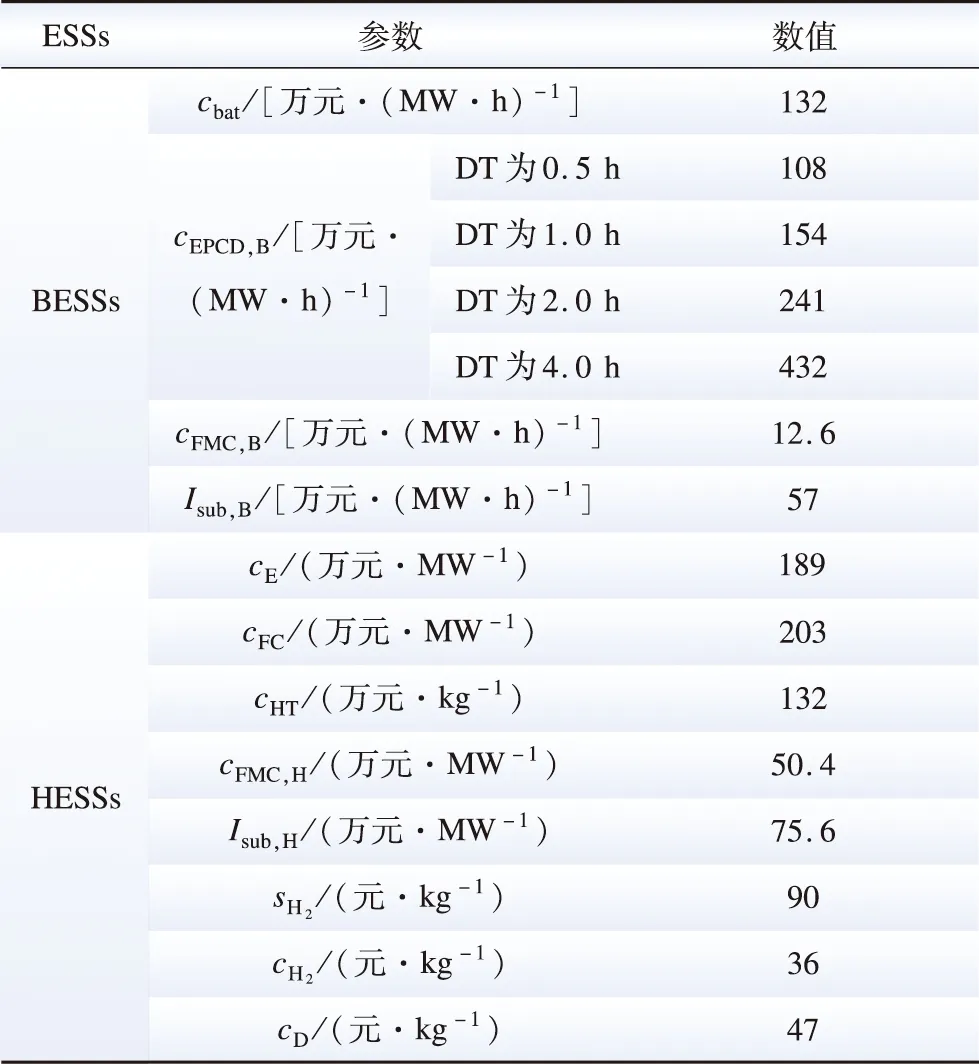
表3 BESSs與HESSs主要數據Table 3 Main parameters of BESS and HESS

表4 分時電價Table 4 Time-of-use electricity price

4.2 算法性能比較

表5給出了2種算法獲得的ESSs接入結果。其中NSGA2的Pareto解集在除LCC最小值的各個目標下的最小(好)值、最大(差)值、平均值均是最小的，可見算法的局部搜索能力很強。因此，NSGA2可以獲得一組更合理的Pareto非支配解集，為決策者提供最佳候選方案。

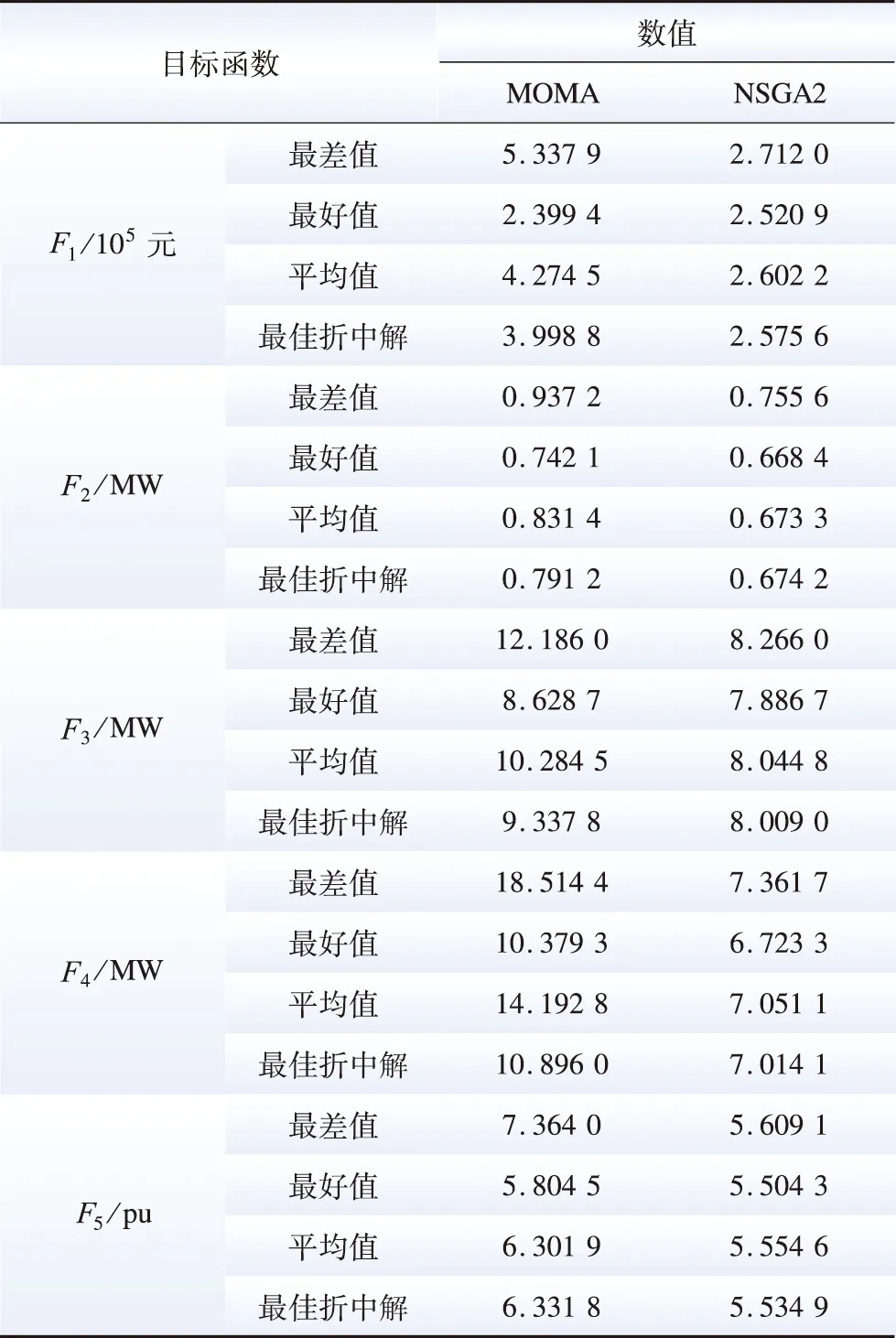
表5 兩種算法的Pareto優化結果Table 5 Pareto optimization results of the model obtained by two algorithms

4.3 結果分析

表6給出了基于EWM的灰靶決策MOMA、NSGA2的優化配置方案。由表6可知，相較于MOMA，NSGA2具有較小的電-氫混合儲能系統LCC、每日的網損、聯絡線交換功率偏差、負荷波動與電壓波動。因此，基于EWM灰靶決策的NSGA2在保證投資運維成本的同時可以給電網帶來最佳的穩定性。

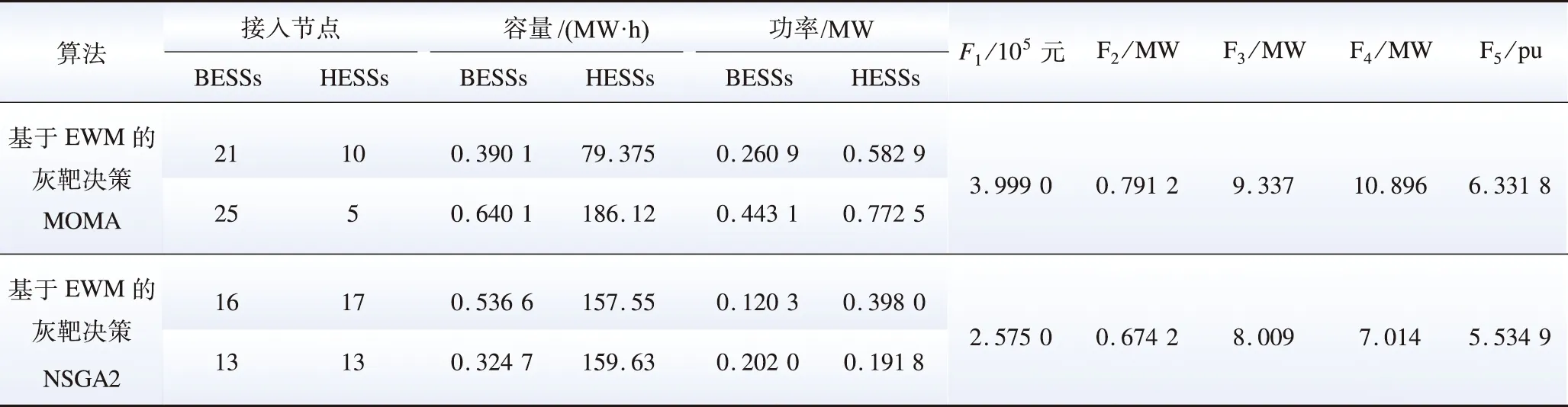
表6 兩種算法獲得的BESSs和HESSs配置方案和優化結果Table 6 BESS and HESS configuration schemes and optimization results obtained by two algorithms

ESSs在各個時刻的充放電功率是在滿足SOC約束與功率約束條件下，考慮電-氫混合儲能系統LCC最小與配電網穩定性最高來確定的。圖5給出了BESSs與HESSs的充放電功率。充放電功率小于0表示ESSs在充電，大于0表示其在放電。

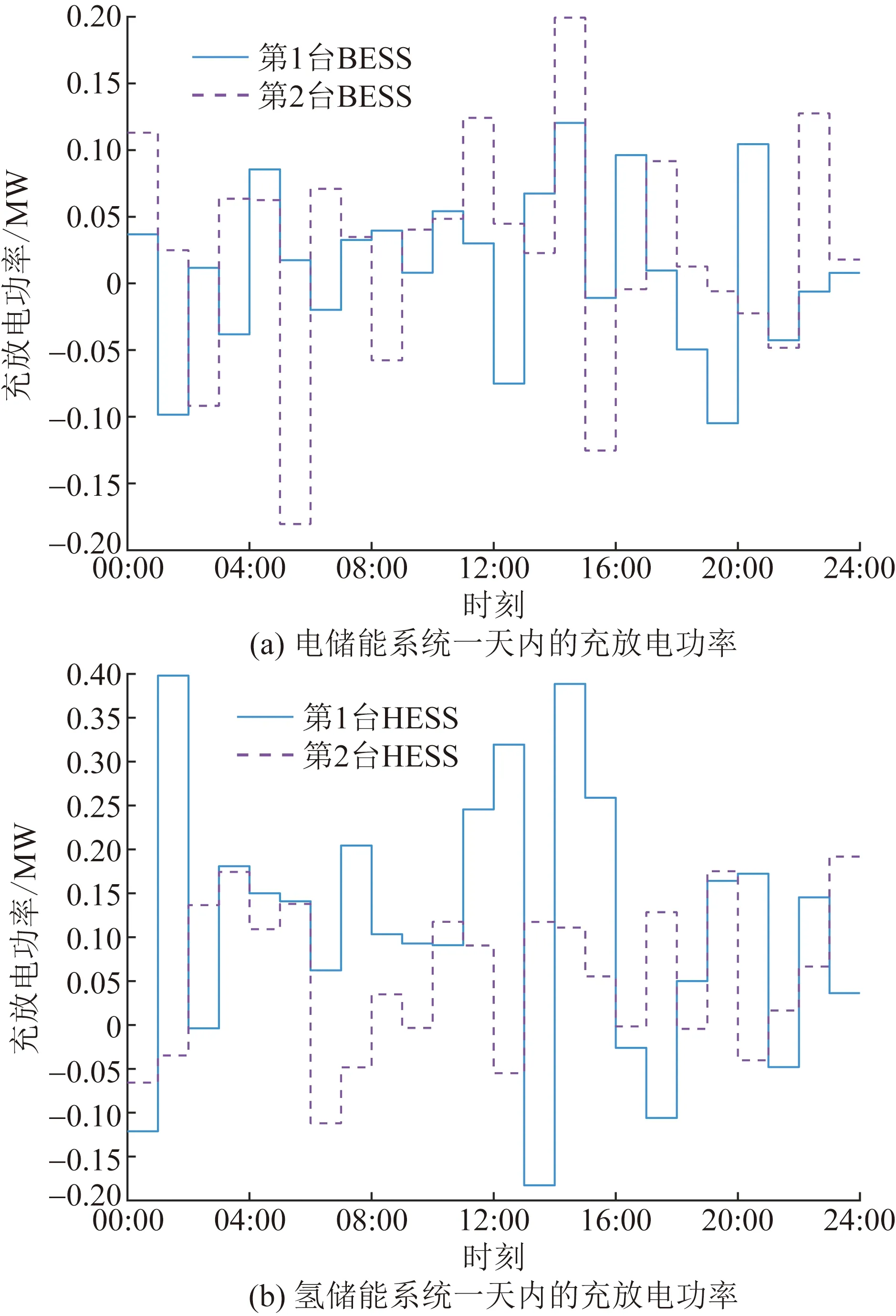
圖5 電儲能系統與氫儲能系統一天內充放電功率Fig.5 Charging and discharging power of BESS and HESS in one day

圖6為基于多目標優化配置電-氫混合儲能系統后的擴展IEEE-33節點聯絡線功率波動、平均節點電壓、平均負荷水平與電壓分布。由圖6可以看出，與未配置電-氫混合儲能系統相比，采用MOMA與NSGA2算法配置電-氫混合儲能系統能在一定程度上改善電網的聯絡線功率波動、負荷水平以及相應的節點電壓水平。并可減小各節點的電壓，防止電壓越限。

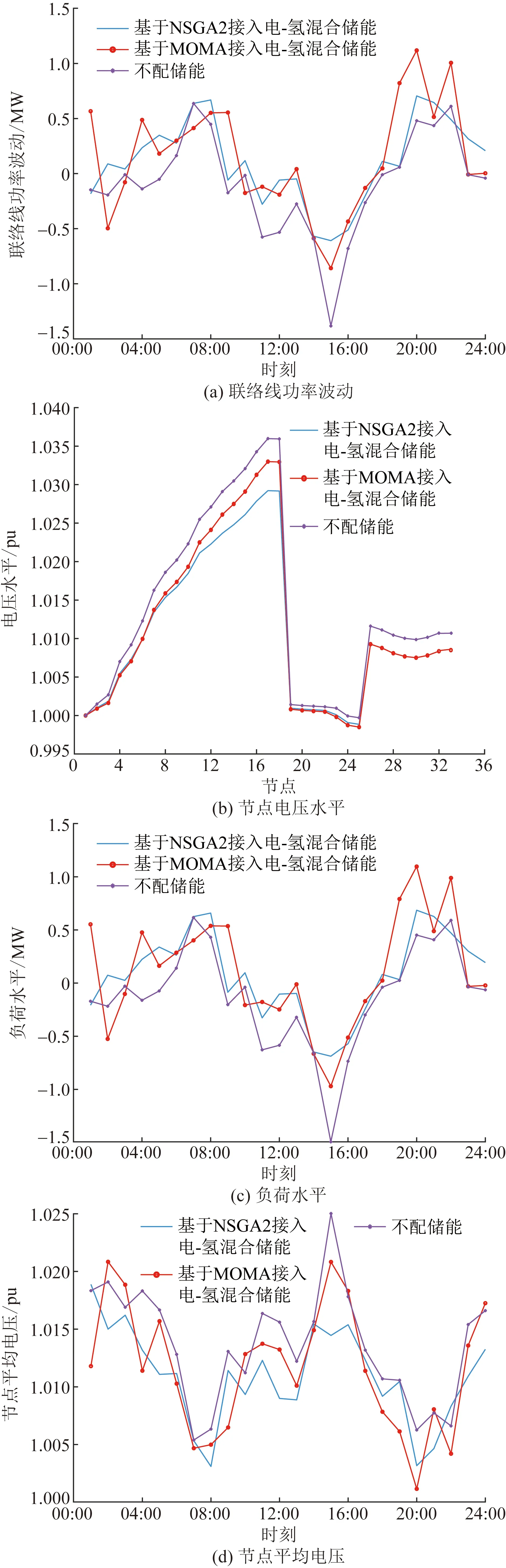
圖6 擴展的IEEE-33節點系統下兩種算法的電網優化結果Fig.6 Optimization results of network obtained by two algorithms in the extended IEEE 33-node system

相較于MOMA，NSGA2對電網各指標的改善效果更為明顯，如電-氫混合儲能系統的LCC減小了35%，網損減少了15%，并且求解時間減少了80%。

為了驗證基于EWM灰靶決策的合理性，本文采用文獻[30]中的方法，將第b個非支配解對應的第a個目標函數映射到(a×i)的二維平面中，公式如下：

(39)

式中：K為隨機參數；fb,a為第b個非支配解的第a個目標函數。

圖7為通過高維笛卡爾坐標映射的(a×i)的二維平面，橫坐標為優化的目標函數，縱坐標為映射后的目標函數值。各目標函數之間用虛線連接。基于EWM的灰靶決策的最佳折中解用紅色實線進行表示。可以看出該折中解始終處于較為合理的范圍，可以避免采取主觀權重而導致對某一目標產生較大偏好。并且非支配解集分布較為廣泛，說明NSGA2算法具有優秀的尋優能力。

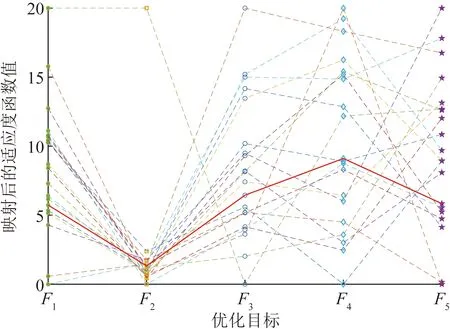
圖7 擴展的IEEE-33節點系統下平行坐標系Pareto前沿Fig.7 Pareto front of parallel coordinate system under extended IEEE 33-node system

為了驗證HESSs的優越性，表7給出了基于NSGA2配置電-氫混合儲能系統與單獨配置BESSs的優化效果對比。可見配置HESSs可以實現經濟效益和電網穩定之間更優的平衡。圖8給出了單獨接入BESSs和同時接入兩種ESSs輸出可視化對比效果。

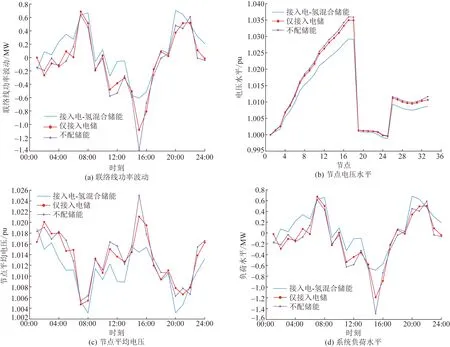
圖8 基于NSGA2算法對比接入不同儲能系統的電網優化結果Fig.8 Grid optimization results of different energy storage systems based on NSGA2 algorithm

表7 配置不同儲能系統的優化結果對比Table 7 Comparison of optimization results with different energy storage configurations

5 結 論

考慮到電-氫混合儲能系統經濟與配電網運行穩定性，本文提出了基于NSGA2的Pareto多目標優化模型，得出以下結論：

1)通過擴展的IEEE-33節點配電網測試，有效地證明了NSGA2具有較強的收斂性能與全局尋優效果，能夠獲得分布廣泛且均勻的Pareto前沿。

2)通過高維笛卡爾坐標映射的二維平面，有效驗證了基于EWM的灰靶決策的最佳折中解的合理性與客觀性。避免采取主觀權重而導致對某一目標產生較大偏好。

3)擴展的IEEE-33節點配電網測試結果顯示，NSGA2能夠在兼顧ESSs經濟性與配電網穩定性的同時改善電壓水平。

此外通過對比僅接入BESSs與接入電-氫混合儲能對配電網穩定的影響，充分體現了HESSs的經濟性以及其對負荷波動、電壓波動等強大的抑制能力。