適應新型電力系統快速頻率支撐需求的混合型儲能系統動態建模及其控制策略分析

鄭華,趙志強，劉斯偉,王東淼，魏楠,王詩銘

(1.華北電力大學電氣與電子工程學院,北京市102206；2.國網新疆電力有限公司經濟技術研究院，烏魯木齊市 830063；3.國網經濟技術研究院有限公司，北京市102209)

0 引 言

構建以新能源為主體的新型電力系統，勢必要解決以風能、太陽能為代表的新能源由于非確定性與隨機波動性造成的電力系統安全穩定問題。大力發展并網運行的儲能系統(energy storage system,ESS)是解決該問題的主要方案之一[1]。ESS不僅在電力調度上具有削峰填谷的作用，而且在暫態時間尺度下可以為電力系統提供額外的電壓與頻率支持，對維持高新能源與電力電子滲透的“雙高”新型電力系統的安全穩定運行具有重要意義。目前，國內外通用的可并網儲能技術主要包括電池儲能、抽水蓄能、飛輪儲能、超級電容器等[2-4]。電池類的儲能技術較為成熟，但容量相對較小；抽水蓄能存儲容量大，但反應時間長，能效較低；飛輪儲能的能量密度低，維護系統安全的成本很高，目前主要用作備用和補充儲能；超級電容具有效率高、響應速度快、功率和能量密度大等優點，但建設成本相對較高。

當前并網儲能系統還是以單一儲能方案為主[5]。單一儲能雖控制難度低、結構相對簡單，但難以滿足新型電力系統貫通不同時間尺度的能量調控需求。因此，充分利用不同儲能技術間的優勢，具有多時間尺度響應特性的混合型儲能系統(hybrid energy storage system,HESS)更適用于新型電力系統[6]。與傳統ESS相比，HESS技術具有明顯的性能優勢和廣闊的應用前景。其中采用蓄電池和飛輪儲能搭配的HESS技術聚集了這兩類儲能技術的主要優勢，展現出建設成本低、功率密度高、能量密度大、響應速度快、循環壽命長等突出優點[7]。由于HESS需要多方面的運行與調配，控制難度增加，動態特性較傳統ESS更為復雜。

PI控制作為最基礎的工業控制器是目前最常用的儲能系統控制技術[8-9]。近年來又發展出許多復雜度更高、魯棒性更好的控制策略，例如H∞控制[10-11]、滑模控制[12-14]、模型預測控制[15]及基于啟發式算法的模糊邏輯控制等[16]。在上述各類基于魯棒技術的控制策略中，相對其他控制技術，H∞控制與滑模控制適用范圍更廣泛，技術更加成熟，具有更加廣泛的工業應用前景。然而，目前新型儲能控制技術的效果定量分析主要通過單機實驗進行，電網側模型通常被極大簡化，且通常只運行于給定的確定性工況下[17]。考慮到我國構建以新能源為主體的新型電力系統的總體戰略目標，儲能控制技術必須確保在高比例新能源滲透、具有高度不確定性和強隨機波動的工作環境下對電力系統動態穩定性提供可靠支撐[18]，然而現有文獻對此論證相對不足。

本文結合當前HESS發展趨勢，選擇以當前儲能技術中具有顯著性價比優勢的飛輪與蓄電池組成的混合儲能系統為研究對象，首先基于半隱式推導法，提出適應大電網仿真及魯棒調頻控制配置的HESS動態建模方法；隨后探討采用PI、H∞以及滑模控制用于ESS調頻的相關特性，并在充分考慮新能源與負荷暫態波動性的情況下，對不同控制策略下飛輪與蓄電池組成的HESS對以新能源為主體的電力系統的動態頻率支撐效果進行直觀比較，進而分析不同控制策略下混合儲能系統快速頻率支撐特性。

1 HESS動態建模

本節將對基于電壓型電力電子變換器(voltage sourced converter,VSC)的HESS結構進行介紹，在此基礎上提出了適用于HESS的通用簡化建模方法，并以飛輪和蓄電池的動態模型為例，簡述所提出的建模方法如何應用于實際HESS。

1.1 ESS基本結構

完備的HESS由不同儲能設備、VSC及其相關控制器構成，具體結構如圖1所示。

圖1所示的ESS經由VSC接口實現并網。本文所構建的ESS模型中將采用文獻[17]中提出的同步交直軸參考坐標下的通用VSC動態模型。該模型包括基于PI控制的電壓外環與電流內環控制器，并對控制器限制環進行了精準模擬，文獻[19]提供了包含DC側控制的詳細全暫態模型。

HESS包含有兩個及以上的儲能裝置，通常由功率型儲能與能量型儲能進行搭配。由于不同類型的儲能具有不同的物理特性，故針對特定的儲能設備選擇能夠最大程度發揮其調頻潛力的控制策略，更加有利于提升HESS的頻率支撐效果。因此，各儲能裝置可配備相互獨立的控制系統。

1.2 HESS動態模型

為構建完善的HESS模型，首先對HESS動態模型提出如下設定：

1)HESS中所有儲能裝置為線性時不變結構；

2)不同控制策略下表示HESS特性的變量與方程總數固定。

基于上述假設，現考慮在并網HESS的特定運行點附近，結合HESS各部分全暫態模型，利用文獻[18]介紹的半隱式推導法，即可得到適應大電網仿真的HESS簡化動態模型：

(1)

式中：x是HESS中與存儲能量相關的勢能和流量，上標“·”表示對時間求導；z代表其他所有變量的向量；u代表存儲元件的輸出信號；vdc和idc分別是VSC的直流電壓和電流；Tx和Tz為對應變量的時間常數；Axx為變量x關于x的微分方程組的雅可比矩陣；Axz為變量x關于z的微分方程的雅可比矩陣，其余A、B參數矩陣可依此類推；Cx、Cz為變量x、z關于idc方程的偏導矩陣，其列數必為1；Du、Dv為變量U、vdc關于idc方程的偏導數；Kx、Kz、Ki為上述方程中與變量無關的定常數部分，此部分對應儲能的初始運行工況，相關數據通常由儲能制造商提供。式(1)中的變量(多個變量集合形成的列向量)為x、z、U、vdc。

式(1)的物理本質為HESS全暫態模型在特定運行點附近的線性化模型，故其中參數可由全暫態模型進行線性化處理后獲得。其中由于HESS全暫態模型階次較高，大部分參數矩陣的推定須由計算程序完成。本文采用電力系統仿真軟件PSAT[19]提供的高階方程雅可比矩陣數值求解算法進行處理。

考慮到HESS中各儲能裝置與其配備的控制策略具有一定獨立性[20-21]，依據假設1)，可通過疊加關系對HESS的輸出進行調節。單個儲能設備狀態均可通過式(1)進行表示，通過矩陣規模的擴列實現HESS建模，1.3節列出了基于飛輪與蓄電池儲能的HESS儲能設備的主要變量。

(2)

需矩陣Azz具有非奇異性，才能實現由式(1)向式(2)的簡化，該條件在儲能模型中總能滿足。式(2)中狀態向量至少要包含2個變量，如代表勢能和流量的xa和xb。對飛輪儲能而言，勢能為電機角速度，流量為電機轉矩；對蓄電池而言，勢能為其內含的電化學能，流量為摩爾流率。儲能裝置中的存儲能量E的計算方式如下:

(3)

式中：i為儲能單元的編號；n為HESS中總儲能單元個數；ρi、βi分別是比例系數和指數系數；χi是xi的參考值。當xi表示ESS的流量或存量時，ρi系數是非零常數。

現采用以下標準形式對式(2)進行化簡：

(4)

1.3 基于蓄電池與飛輪儲能的HESS動態模型

飛輪儲能(flywheel energy storage,FES)以機械動能形式儲存能量，是一種典型的功率型儲能系統，具備快速響應系統頻率變化，提供緊急頻率救助的潛力。蓄電池儲能(battery energy storage,BES)以化學能形式儲存能量，單位容量造價相較飛輪儲能低，放電速率較飛輪儲能而言較慢，可用作能量型儲能。基于FES與BES共同構成HESS系統，兼具快速頻率響應與長時間續航能力。

文獻[23]中具體描述了基于籠型感應電機的FES在同步交直參考系下的數學模型，文獻[24]提出了目前最為通用的BES的充放電模型，即Shepherd模型。基于上述兩種儲能設備的全暫態模型，可采用1.2節所介紹的方法將其簡化為適應大電網仿真的動態模型，其標準數學形式如式(4)所示。

其中FES相關變量如下：

(5)

式中：ωr為飛輪轉子角速度；Te為電氣轉矩；vΘ為定子交直軸、轉子交直軸的電壓變量集合；iΘ與ΨΘ分別為同類的電流與磁通變量集合；ωs為定子側電氣頻率；HFES為飛輪等效慣性常數。

其中BES相關變量如下：

(6)

式中：Qe為蓄電池當前存儲能量；vb為電池電壓；ib為充放電電流(受低通濾波器影響)；im為電池電流；vp為極化電壓；?為變換器占空比；Qn為蓄電池額定容量。

2 HESS控制器設計

本節將系統闡述可用于1.3節所述HESS的PI、H∞和滑模控制器的主要特性和設計方法，并給出實現HESS較優調頻效果的參數取值。

2.1 PI控制

用于儲能控制的典型PI控制器結構如圖2所示。

圖2 儲能系統PI控制Fig.2 PI control for ESS

該控制器的主要環節包括死區、低通濾波器、PI調節器和存儲輸入限制器，旨在降低因ESS能量飽和產生的瞬時變化效應的影響[25]。

PI調節器由比例增益Kpu和具有積分增益Kiu、積分偏差系數Hd的積分器組成。這些參數通常通過反復試驗或極點配置技術進行整定，本文案例分析部分采用的PI設定調頻死區為0.000 1 pu，FES采用的PI控制參數為：

(7)

BES采用的PI控制參數為：

(8)

PI控制器的設計實現難度系數較低，而且其控制環節的參數整定可獨立于儲能裝置特性。但是，文獻[24]證明，儲能系統的不確定性和拓撲變化會顯著破壞PI控制器的性能，進而威脅整個系統的性能。該結論表明，新一代儲能設備可能需要采用更先進的魯棒性更好的控制策略，如H∞和滑模控制。

2.2 H∞控制

H∞控制是近年被廣泛研究的一種最優控制方法。傳統最優控制的主要目的是設計能在不確定擾動下仍然滿足閉環系統內部穩定要求的最優控制函數。由于求解儲能系統能量增益最小化過于復雜，難以實踐。因此，H∞控制器通過最小化圖3所示系統閉環傳遞函數的H∞參數，對最小能量增益進行近似估算，進而實現最優控制。

圖3 儲能系統H∞控制Fig.3 H∞ control for ESS

然而即使只考慮經簡化后的線性時不變系統，設計H∞控制器依然難度較大。以下簡要闡述針對于1.2節中所提出的HESS模型的H∞控制器設計方法。

(9)

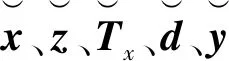
(10)

式中：xa和xb是式(4)的狀態變量；xu是控制器的輸出，存在如下調節關系：

(11)

式中：Ku為正權重系數，用于結合控制器的輸出和儲能設備的轉換器，通過式(11)所示的調節關系進而實現HESS的下垂控制。

時不變參數矩陣：

(12)

外部擾動：

(13)

式中：xf為各狀態變量遭受的擾動。

控制器測量輸出：

(14)

式(9)目標系統對應H∞控制的適定性約束如下所示：

式中：I為單位對角矩陣；rank為矩陣階數函數；dim為向量維度函數。

上述約束條件4)—7)表明，相關狀態矩陣一定是非奇異的。

若式(9)滿足上述所有條件，則可通過求解目標系統對應的Riccati方程(詳細求解方法見文獻[26])完成對圖3所示的K∞的設計，其具體結構為：

(15)

(16)

其中的中間變量可表述為：

(17)

第3節算例所選用的HESS模型由Riccati方程解得保守性γ=9.3×10-9的情況下，控制器K∞所選用的控制參數如下：

(18)

上述參數魯棒性較強，故對FES與BES采用同一套參數。

2.3 滑模控制

滑模控制器的基本原理是利用切換控制邏輯，使動態結構系統的軌跡遵循給定的路徑，又稱為滑動面(通常表達為S)。如存在滑動面滿足Lyapunov漸近穩定性條件，則控制策略一定對不確定性干擾具有魯棒性[27]。但滑模控制也具有一些缺點，其中最顯著的就是切換邏輯容易因物理設備的控制延遲、滯后和死區影響產生抖振效應[28]。此外，滑模控制是一種模型依賴型技術，其控制效果與建模準確性息息相關。

適用于1.2節提出的HESS模型的滑模控制方法可表述如下：

u=ueq-KSMsign(S)

(19)

式中：ueq為滑模運行期間控制的連續分量；KSM為正增益，旨在減少外部擾動和干擾所帶來的影響。

將式(4)中的勢能xa和流量xb代入，可推知滑動面：

S=xf-sabxaxb

(20)

式中：xf在此處為要調節的測量信號的濾波偏差；sab為滑動面S上的單位變量。

在式(4)所對應的平衡點xo附近線性化式(20)，可得：

S-So=(xf-xfo)-sab[x2o(xa-xao)+
xao(xb-xbo)]

(21)

式中：狀態變量x的標定與2.2節相同，下標“o”表示在平衡點處取值。

考慮到在平衡點時有So=0和xfo=0。因此：

S=xf+sx(x-xo)

(22)

式中：sx=-[sabxbosabxao]。

(23)

將式(23)代入式(4)可知：

(24)

式(24)中對應的ueq的連續分量定義如下：

(25)

結合式(19)與式(24)—(25)可完成適用于式(4)所描述的HESS的滑模控制器。

由于滑模控制所針對的控制對象對響應速度具有較高要求，BES的動態響應速度難以展現滑模控制的控制效果。因此，在本文所探討的HESS中，僅考慮滑模控制在FES上的應用，并取控制參數為：

KSM=10-6

(26)

并設定式(25)中出現的參數矩陣為：

(27)

3 算例分析

本節采用IEEE標準測試系統，即新英格蘭10機39線系統進行實驗，以對比第2節所述控制策略在FES與BES組合構成的HESS上的控制效果。為準確模擬以新能源為主體的電力系統的動態特性，本文所采用的測試系統將傳統的10機系統中的部分同步火電廠替換為風電場與光伏電站，使新能源滲透率達到46.1%，并搭配總容量占新能源總裝配量30%的兩個HESS。系統的拓撲結構如圖4所示。本節的仿真采用基于Matlab的電力系統機電暫態仿真平臺PSAT進行實驗。圖4所示的拓撲中各新能源場站的裝機容量及其在穩定運行點時的出力如表1所示。

圖4 具有高新能源滲透率的改良新英格蘭系統Fig.4 Modified New England system with high penetration rate of new energy

表1 改良新英格蘭系統新能源電源參數Table 1 Parametevs of the renewable energy power sources for modified New England system

風電場采用適應電力系統機電暫態仿真的永磁風機聚合等值模型,光伏電站采用等效光伏電池模型，上述兩個模型的具體數學表達式均可見文獻[29]，假定風電場和光伏電站均不參與調頻。

考慮到BES具有較強的續航能力，而FES在動態時間尺度下具有較強的電壓與頻率支持效果，因此圖4中所示的兩個HESS系統中BES占總容量的65%，FES占總容量的35%。為充分考慮系統中的隨機波動影響，采用基于韋伯分布的動態風速模型,太陽能與負荷的波動則采用經典Ornstein-Uhlenbeck波動方程進行模擬。所考慮的N-1故障為37號母線上的同步發電機脫網。在此情況下，若系統中不存在HESS，則系統將發生頻率崩潰。

現考慮系統中具有如圖4所示的兩個HESS，其控制策略有如下3種：

1)BES與FES均采用PI控制；

2)BES與FES均采用H∞控制；

3)BES采用H∞控制，FES采用滑模控制。

系統中的兩個HESS完全一致，如圖4所示，一個位于2號母線，一個位于20號母線。在暫態仿真開始時的系統工作點上假定HESS均不向電網輸出有功功率。HESS的具體調頻控制參數已在第2節進行了說明，表2列出了HESS中FES與BES的關鍵參數。

表2 HESS具體參數Table 2 Parametevs of HESS

圖5展示了在特定隨機波動情況下上述三種控制策略下N-1事件發生前后的系統慣性中心(center of inertia,CoI)頻率演化軌跡。其中，N-1事件發生于仿真開始后40 s。慣性中心頻率fCoI定義如式(28)所示：

(28)

式中：N為電力系統中同步電源總個數；fi、Hi分別為第i個同步電源的頻率及其等效慣性常數。

由圖5所示軌跡可知，系統N-1故障響應的時長約為40 s，隨后的暫態行為由系統中的波動性主導。

圖5 改良新英格蘭實驗系統動態頻率衍化特性Fig.5 Dynamic frequency evolution characteristics of modified New England system

考慮到本實驗系統不包含二、三級頻率控制，故可將總時長120 s的仿真劃分為3個不同階段：0～40 s為前故障運行狀態；40～80 s為故障響應過程；80～120 s為后故障運行狀態。為避免由仿真隨機性造成的不確定性影響，本節采用蒙特卡洛實驗法，選用相同的概率分布隨機波動模型來控制變量，重復1 000次實驗，并對結果求取平均值，以準確反映不同HESS控制策略下系統的頻率動態特性，相關實驗結果如表3所示。表3中，σω為對應時間范圍內頻率波動的標準差，Δfnadir為故障響應過程中頻率最低點與額定工況50 Hz的偏差。

由表3可知：

表3 蒙特卡洛實驗評估下的改良新英格蘭系統慣性中心頻率動態特性Table 3 Monte Carlo experimental evaluation of frequency dynamics in the improved New England system

1)前故障運行狀態下，三種不同的控制策略均能對風速與負荷的隨機波動進行有效平抑，其中PI控制效果最差，但仍將頻率波動標準差減小了43.94%；H∞-滑模控制效果最好，可將正常運行狀態下頻率波動標準差降低56.74%。

2)故障響應過程中，三種不同的控制策略均能確保為系統提供可靠的頻率支撐，避免系統崩潰。其中PI控制效果較差，以PI控制效果為基準，H∞和H∞-滑模控制效果在降低頻率暫態極限偏差和抑制頻率波動范圍方面均有顯著提升，其中H∞-滑模控制頻率支撐效果略強于H∞控制。

3)后故障運行狀態下，在無二、三級頻率控制調節的情況下，三種控制效果的頻率偏差近似，但仍以PI控制較差(頻率波動標準差達到0.455 Hz)，H∞-滑模控制最優(頻率波動標準差為0.427 Hz)。

4 結 論

本文利用半隱式線性化方法推導化簡了全暫態儲能模型，進而構建了適用于新型電力系統動態特性分析的具有快速頻率支撐能力的HESS的簡化建模方法，并分析了PI、H∞及滑模控制策略在HESS調頻作用中的應用潛力。基于改良的IEEE標準系統，在考慮新能源與負荷隨機波動性情況下，對基于BES與FES的HESS調頻控制策略的效果進行了對比。根據實驗結果，可以得出以下結論：

1)在系統中安裝由BES與FES組合的HESS能顯著提升系統的頻率安全穩定性。

2)通過將滑模控制器應用于FES以及將H∞控制器應用于BES，可以實現最小的動態頻率波動，從而實現HESS的最佳魯棒性能。

3)雖然PI控制器的動態性能總體而言是3種技術中最差的，但它對電力系統的頻率隨機波動仍具顯著的平抑效果，且可對故障進行準確響應。考慮到PI控制的設計相對魯棒性控制器而言更簡單，故在當前情況下PI控制在HESS中仍具有實用價值。