基于整體傳遞矩陣法的導向工具偏心主軸動力學特性

唐博， 王鵬， 張紅， 馮定*

(1.長江大學機械工程學院， 荊州 434023； 2.湖北省油氣鉆完井工具工程技術研究中心， 荊州 434023)

指向式旋轉導向工具是目前國內外石油鉆井領域先進的定向鉆井工具，其具有鉆井效率高和惡劣環境下鉆井能力高等諸多優點，適應目前油藏開發的發展趨勢[1-2]。在導向工具鉆井作業時，主軸的動力學特性是旋轉導向系統可靠性的決定性因素之一[3]，導向工具主軸的動力學行為與井眼軌跡設計和控制密切相關。因此，有必要深入研究導向工具主軸的動力學特性。

目前，國外關于旋轉導向系統動力學特性研究方面主要集中于底部鉆具組合的動力學特性研究[4-6]，而對導向工具主軸動力學特性的探討較少。中國對導向工具主軸的動力學特性研究主要集中在以下幾個方面：馮定等[7]基于動態有限元積分算法，分析了導向工具主軸轉速、偏心距及鉆壓對主軸力學行為的影響。張光偉等[8]基于有限元法進行了導向工具主軸振動的模態分析。張紅[9]采用能量法建立了導向工具主軸的動力學方程。田偉康[10]使用傳遞矩陣法求出了主軸橫向振動的固有頻率。

綜上所述，中國關于導向工具主軸動力學特性方面常用的研究方法主要包括有限元法[11]、能量法以及傳遞矩陣法。但有限元方法和能量法建模過程煩瑣，求解耗時較長[12]，相比于前兩種方法，傳遞矩陣法主要優勢在于建模靈活和計算求解效率較高[13]，且中國對導向工具主軸的動力學特性研究并沒有考慮導向工具外殼和軸承對主軸的影響，使得計算結果不夠精確。因此，綜合考慮導向工具外殼與主軸的相互作用，采用整體傳遞矩陣法[14]，建立了工作狀態下指向式導向工具外殼-軸承-主軸系統動力學模型。基于上述模型展開了導向工具偏心主軸的動力學特性分析，推導了偏心主軸任意節點的撓度、轉角、彎矩和剪力方程，并通過主軸測點實驗分析驗證了力學模型的合理性。

1 導向工具系統動力學模型

圖1為指向式導向工具結構示意圖。主軸通過上支撐軸承和下支撐軸承與外殼連接，組成了外殼-軸承-主軸動態耦合系統。考慮外殼撓曲變形對主軸力學行為的影響，采用整體傳遞矩陣法建立導向工具外殼-軸承-主軸系統動力學模型，如圖2所示。在簡化過程中，按照質心不變的原則[15]，將主軸和外殼均離散為采用N段無質量彈性軸聯接的集中質量[16]；軸承和夾持機構簡化為具有徑向剛度和轉動剛度的彈簧。此外，為了確保外殼與主軸具有相同的單元數，在主軸鉆頭段對應的外殼處引入長度和質量均為零的虛段外殼，使之與主軸分段邏輯對齊[14]。

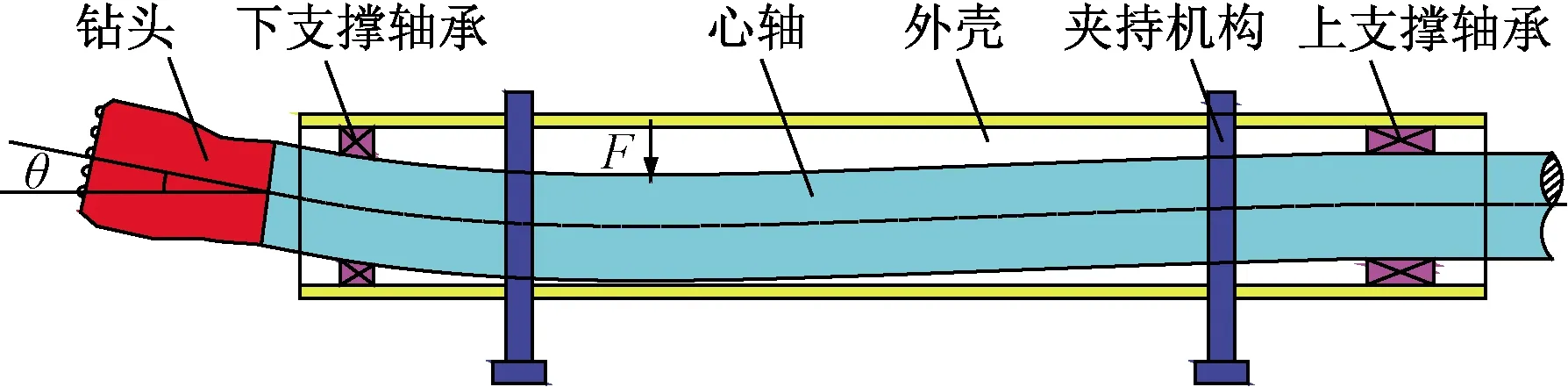
圖1 指向式導向工具結構示意圖Fig.1 Schematic diagram of point-bit steerable tool

F1為偏置機構給主軸的偏置力，N；F2為偏置機構給外殼的偏置 力，N；Kr為外殼與夾持機構接觸的徑向剛度，N/m；Kθ為外殼 與夾持機構接觸的轉動剛度，N·m/rad；Kc為耦合軸承徑向 剛度，N/m；Kch為耦合軸承轉動剛度為，N·m/rad圖2 外殼-軸承-主軸系統動力學模型Fig.2 Housing-bearing-spindle system dynamics model

根據等截面梁的計算結果[16]，如果要求的導向工具主軸的臨界轉速計算誤差小于1%，那么分段總數N應滿足

N≥1+5.34r

(1)

式(1)中：N是需要劃分的軸段數；r為需要求解的固有頻率階數。

設主軸和外殼任意節點i的狀態矢量分別為

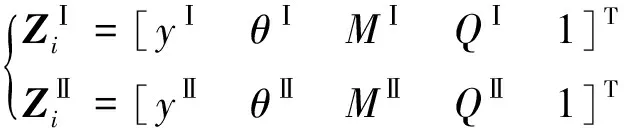
(2)

則將主軸和外殼狀態矢量合并置于同一向量中可得到整體傳遞矩陣的狀態矢量，即

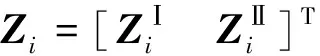
(3)

式(3)中：y為撓度，m；θ為轉角，rad；M為彎矩，N·m；Q為剪力，N。

根據力學平衡條件和材料力學理論[14]，可以分別寫出主軸和外殼的質量—梁單元傳遞矩陣，其傳遞矩陣形式如下所示。

主軸質量-梁單元傳遞矩陣為

(4)

外殼質量-梁單元傳遞矩陣為

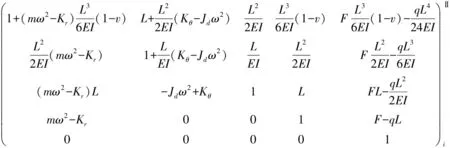
(5)

式中：v為剪切變形系數；EI為無質量軸段的抗彎剛度，N·m2；G為剪切彈性模量，GPa；L為無質量軸段長度，m；A為橫截面面積，m2；F為偏置力，N；q為重力分布載荷，N/m；Jp為極轉動慣量，m2；Jd為直徑轉動慣量，m2；m為集中質量，kg；ω為固有頻率，Hz。

將式(4)和式(5)合并可得到外殼-主軸整體單元傳遞矩陣為

(6)

此外，由于導向工具主軸與外殼通過軸承連接在一起，如圖3所示。

圖3 外殼與主軸耦合示意圖Fig.3 Schematic diagram of coupling between housing and spindle

因此，根據整體傳遞矩陣法，主軸和外殼在耦合處需要通過耦合矩陣滿足協調條件[13]，設耦合點在節點i處， 根據協調方程[14]可推導出外殼與主軸的耦合矩陣為

(7)

由上述可知，在外殼-軸承-主軸系統動力學模型中，整體狀態矢量存在傳遞關系，即

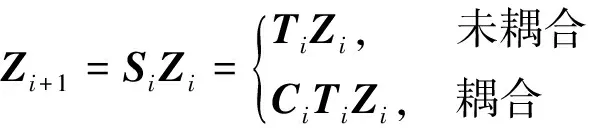
(8)

式(8)中：Si為外殼-軸承-主軸系統整體傳遞矩陣。

2 導向工具動力學特性分析

2.1 導向工具整體臨界轉速和振型

外殼-軸承-主軸系統動力學模型中主軸與外殼端點處節點狀態矢量相同，導向工具第1個節點是鉆頭端，第N+1個節點是上支撐軸承端。

上支撐軸承端為固定狀態不變，即

ZN+1=[0Ⅰ0ⅠMⅠQⅠ10Ⅱ0ⅡMⅡQⅡ1]T

(9)

非鉆進工況下，鉆頭端節點為自由狀態，即

Z1=[yⅠθⅠ0Ⅰ0Ⅰ1yⅡθⅡ0Ⅱ0Ⅱ1]T

(10)

且第一個節點狀態矢量和第N+1個節點狀態矢量之間可通過式(8)表示為

ZN+1=SZ1

(11)

式(11)中：S=SNSN-1…S3S2S1

則將式(9)和式(10)代入式(11)可得方程AX=B為

(12)

式(12)中:Sa,b為S矩陣的第a行第b列的元素。為使式(12)有非零解，則其特征行列式必須為0，即

A=0

(13)

對特征方程式(13)求解即可得到非鉆進工況下導向工具整體固有頻率和臨界轉速，將固有頻率代入式(12)，解此方程組就可得到鉆頭端的狀態矢量，再將固有頻率和鉆頭端的狀態矢量代入式(11)即可得到導向工具對應于此階固有頻率的振型。

2.2 偏心主軸軸身幾何方程和力學方程求解

將導向工具主軸的工作轉速代入式(12)進行求解即可得到節點1處狀態矢量Z1。將主軸的轉速ω和狀態矢量Z1代入式(8)即可得到偏心主軸任意節點i處的撓度、轉角、彎矩和剪力為

(14)

式(14)中：S=Si-1Si-2…S1；Sa,b為傳遞矩陣S的第a行第b列的元素。

3 實例計算

3.1 導向工具系統整體固有頻率和振型

基于上述力學模型，進行固有頻率和振型計算。以指向式旋轉導向工具為例,其外殼外徑為180 mm,內徑為150 mm,總長為2 685 mm,彈性模量為211 GPa,泊松比為0.3,質量為164 kg,主軸外徑為70 mm,內徑為40 mm,主軸總長為3 063 mm, 彈性模量為195 GPa,泊松比為0.28,質量為62 kg。

(1)固有頻率計算：主要分析導向工具前三階固有頻率,根據式(1)計算應將導向工具劃分為17段,即N=17,具體的劃分如圖4所示，在節點4處和節點17處分別為下支撐軸承和上支撐軸承所對應的位置,在節點5處和節點16處為夾持機構對應的位置,節點7處為偏置機構對應的位置。

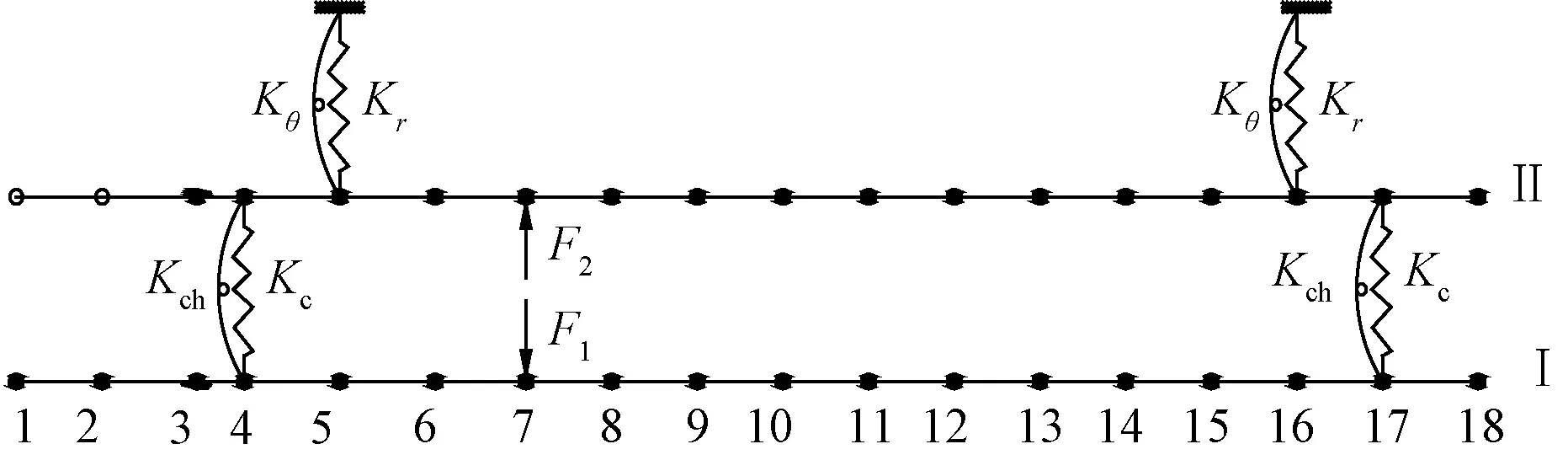
圖4 導向工具具體劃分示意圖Fig.4 Schematic diagram of steerable tool concrete division

對式(13)求解可得到導向工具系統前三階固有頻率，分別為199.716、550.724、946.690 Hz，由于導向工具主軸的最高工作轉速為200 r/min，低于一階臨界轉速，因此導向工具在工作過程中不會產生共振現象，安全性和可靠性可以得到保障。

(2)主軸振型計算：主軸偏置機構施加偏置力F1使主軸節點7處撓度為6 mm時，將前三階固有頻率和節點1處狀態矢量Z1代入式(14)即可得到相應的主軸前三階振型，如圖5所示。

從圖5可知，從鉆頭處到下支撐軸承處，越靠近下支撐軸承，主軸前三階固有振型振幅越小，且下支撐軸承處振幅接近零；從下支撐軸承到偏置機構處，越靠近偏置機構，一階和二階固有振型振幅越大，而三階固有振型振幅變化狀態為先減小后增大(小-大)；從偏置機構到上支撐軸承處，隨著靠近上支撐軸承，主軸一階振型振幅變化狀態為大-小，主軸二階振型振幅變化狀態為小-大-小，主軸三階振型振幅變化狀態為大-小-大-小，且在上支撐軸承處前三階振型振幅均為零。可見，階數越高，主軸振型越復雜。

3.2 主軸測點偏移量計算

為與下文導向工具室內實驗結果作對比分析，此處主要計算導向工具主軸測點偏移量。主軸測點[9]為近鉆頭端、距離下支撐軸承100 mm處，為計算方便，將其設置為主軸節點3，即式(14)中i=3，分別代入工具主軸轉速30、60、90 r/min可得不同偏心距下主軸測點偏移量，結果如表1所示。

從表1可知，當導向工具內外偏心環合成偏心距不變時，轉速對主軸測點偏移量影響較小；當轉速一定時，偏心距與主軸測點偏移量成正比關系。

表1 測點偏移量實驗結果均值、理論結果和誤差

4 室內實驗驗證

為驗證本文所提出的力學模型，以現有的井眼軌跡控制工具實驗臺架[9]為基礎，開展主軸測點偏移量實驗，測得不同偏心距和轉速下電渦流位移傳感器處主軸的偏移量，將實驗數據處理結果與理論計算結果進行對比分析，來驗證導向工具外殼-軸承-主軸系統力學模型理論分析的合理性，測試裝置如圖6所示，其具體參數在3.1節中已敘述。

4.1 主軸測點偏移量測試原理

指向式導向工具主軸測點偏移量測試原理圖如圖7所示。

圖6 井眼軌跡控制工具實驗臺架Fig.6 Well trajectory control tool test bench

圖7 測試原理圖Fig.7 Test schematic

采用四個電渦流位移傳感器，分別布置于主軸上C-C′截面上對應主軸外徑上(在圖中EFGH處)，測量主軸C點處變形后點C′的橫坐標x1、x2，縱坐標y1、y2，主軸截面中心沿x軸、y軸兩個橫向運動耦合的合位移為exy，即主軸測點偏移量為

(15)

4.2 主軸測點偏移量實驗結果及誤差分析

將對應偏心距和不同轉速下測得的實驗數據取平均值，并將實驗結果、理論結果和誤差計算匯總，如表1所示。從表1可以看出，主軸在30、60、90 r/min三種轉速下，理論計算結果與實驗結果吻合度較好，最大誤差為 6.48%，滿足工程需要。

通過上述分析可知，實驗測得的數據與理論計算的結果較為一致，因此建立的動力學模型合理且可靠。

5 結論

(1)綜合考慮了指向式導向工具外殼和主軸的相互作用，基于整體傳遞矩陣法，建立可用于分析導向工具偏心主軸動力學特性的外殼-軸承-主軸系統動力學模型。

(2) 通過力學模型計算了指向式旋轉導向工具前三階固有頻率和主軸偏置6 mm時的前三階振型，得出結論，主軸最高工作轉速200 r/min遠小于一階臨界轉速，因此，在導向工具主軸工作過程中不會發生共振現象，在工作轉速范圍內可以安全、穩定地運轉。

(3)通過力學模型推導了導向工具偏心主軸任意節點處的幾何方程和力學方程，并結合實例，計算了不同轉速和不同偏心距下的主軸測點偏移量。

(4)利用高造斜率井眼控制工具的實驗臺架對不同轉速和不同偏心距下主軸測點偏移量進行實驗，實驗測得的數據與理論計算結果非常接近，最大誤差僅為6.48%，驗證了所建力學模型的合理性。