斑巖礦床侵入體頂部破裂系統形成的力學機制:多場耦合數值模擬的啟示

常成， 羅綱

1 中國科學院計算地球動力學重點實驗室， 中國科學院大學地球與行星科學學院， 北京 100049 2 武漢大學測繪學院， 武漢 430079 3 武漢大學地球空間環境與大地測量教育部重點實驗室， 武漢 430079

0 引言

斑巖礦床是一種重要的經濟礦床，其產出的金屬包括了全世界約75%的銅，50%的鉬，25%的金，以及少量的銀、鉛、鋅等(Kirkham and Sinclair, 1995; Sillitoe, 2010; Richards, 2003, 2009, 2013; Richards and Mumin, 2013；Hou et al., 2015).在斑巖礦床中，銅和鉬元素通常以網脈狀或脈狀-浸染狀產出于花崗質侵入體的頂部和周圍，并賦存于破裂的巖石中(Tosdal and Richards, 2001；Guillou-Frottier and Burov，2003;Sillitoe, 2010).近年來對斑巖礦床的研究表明，在不考慮熱液與圍巖相關的化學反應因素的情況下，侵入巖體周圍的破裂、破碎帶和角礫巖筒等破裂系統既是含礦熱液的導流通道，又是含礦熱液中礦質沉淀和最終礦體賦存的成礦空間(Burnham, 1985; Tosdal and Richards, 2001; Guillou-Frottier and Burov，2003; Stephens et al., 2004; 劉亮明, 2011; Dilles and John, 2021).因此，研究斑巖礦床侵入體周圍破裂形成的物理力學機制，對于理解斑巖礦床的礦體就位過程以及找礦勘探工作都具有重要的指導意義.

斑巖礦床是典型的與巖漿有關的熱液成礦系統.這類成礦系統是復雜的多物理場耦合系統，主要受到溫度(thermal)、流體在孔隙介質中的流動(hydraulic)、力學作用(mechanical)和水-巖化學反應(chemical)四種主要因素的耦合控制(Hobbs et al., 2000; 池國祥和薛春紀, 2011; Poulet et al., 2012; Zou et al., 2017).以斑巖侵入體周圍破裂系統的形成為例，前人的研究表明，淺部的花崗巖侵入體是成礦熱液集中和熱力學作用特別強烈的區域；高溫花崗巖侵入體的加熱作用、巖體中析出的巖漿水和揮發分、巖體侵入有關的力學過程以及上述過程之間的相互作用控制著侵入體周圍破裂系統的形成(Tosdal and Richards，2001；Guillou-Frottier and Burov，2003).所以，在不考慮復雜的水-巖化學反應和礦質沉淀的情況下，全面地研究斑巖礦床中侵入體周圍破裂系統的形成，需要包括熱(T)-流體(H)-力學(M)三個因素的耦合作用，即THM耦合(Hobbs et al., 2000; Guillou-Frottier and Burov，2003; Poulet et al., 2012).

THM耦合模型已廣泛應用于多項工程及災害研究，包括地下核廢料的貯藏、油氣的產生和儲存、地熱能的開采、滑坡的產生和斜坡的穩定性等等(Jing and Feng, 2003).但是，很少有研究者將其應用到熱液成礦系統這樣的地質時間尺度問題(Poulet et al., 2012).原因主要有三個：第一，傳統的礦床學研究方法注重于成礦溫度和化學反應過程，對熱液流體的流動模式以及成礦系統的動力學機制研究不足；第二，地球科學家們經常將復雜地質過程和問題概念化，并且識別出地質過程的一到兩個主控因素進行調查研究；第三，三種以上的物理化學因素的耦合屬于復雜的非線性多場耦合求解問題，計算常常不收斂，且所需的計算量很大.這些限制條件使得成礦動力學研究常常忽略了復雜的相互耦合反饋機制，但這些反饋機制常常是十分重要的(Hobbs et al., 2000; Guillou-Frottier and Burov，2003; Schardt and Large, 2009; Poulet et al., 2012).

目前大部分相關研究是對地質現象的觀測(Tosdal and Richards，2001；Sillitoe, 2010)，或者通過礦床中不同的破裂類型和應力莫爾圓來推斷破裂的形成，而對巖漿侵入體周圍的破裂形成力學機制研究較少(Stephens et al., 2004；劉亮明, 2011; Japas et al., 2021).前期研究者們通過解析的力學公式初步研究了侵入體周圍破裂形成的力學機理，但隨著計算機技術和數值計算方法的發展，數值模擬研究方法逐漸被用來進一步深入解釋侵入體周圍破裂形成的力學機制.Koide和Bhattachar(1975)通過推導解析的彈性力學公式和塑性屈服準則，初步研究了侵入巖體頂部可能形成的破裂樣式和不同力學性質的破裂分帶.Sartoris等(1990)通過有限元方法模擬了淺部巖漿房的不同形狀、不同頂部侵入壓力以及不同力學參數條件下巖漿房周圍破裂的形成，但是沒有耦合熱和流體的作用.Guillou-Frottier和Burov(2003)通過耦合熱傳導、熱膨脹與Mohr-Coulomb塑性屈服準則，研究了高溫侵入體的熱效應導致的巖體頂部破裂形成的動力學機制，但是沒有考慮流體的作用；Zhang等(2012)通過耦合熱傳導與應力應變，建立了考慮剪切生熱的位錯-蠕變力學本構，研究了在擠壓和拉張背景下巖漿房周圍大斷層的形成樣式，但是該研究依然沒有考慮流體對破裂的影響，并且其破裂的形成主要是構造加載導致的，僅對賦存于構造運動下形成的大斷層中的礦床(剪切帶型金礦床)具有重要意義.綜上所述，對于斑巖成礦系統中巖漿侵入體周圍的破裂形成力學機制研究，目前還缺乏熱-流體-力學三場耦合的數值模型及其模擬研究.

為了研究巖漿熱液成礦系統的物理力學過程及演化，本文首先建立了一個概念性的簡化的柱狀巖漿侵入體侵入到圍巖中的二維孔隙熱彈性平面應變有限元模型，通過耦合熱傳導、孔隙流體流動和應力應變(THM耦合)，分析了高溫巖漿的侵入對圍巖中應力和應變狀態的擾動和影響，驗證了模型的正確性.然后，在模型中加入塑性，計算了塑性應變(即破裂)的形成與演化，通過分析偏應力、平均應力及孔隙流體的演化，來解釋侵入體周圍圍巖的破裂形成和發育的力學過程.模擬計算發現偏應力在侵入巖體頂部圍巖的集中是導致巖體頂部破裂形成的主要原因.最后，依據青藏甲瑪銅多金屬斑巖礦床的實際礦床剖面，建立了一個二維平面應變孔隙熱彈塑性有限元模型，計算了侵入巖體頂部圍巖破裂的形成.模型結果顯示侵入巖體頂部圍巖破裂發育情況與甲瑪礦床巖體頂部的斑巖礦體和角巖礦體的容礦破裂系統具有一致性.這一結果解釋了侵入體頂部圍巖破裂系統形成和發育的力學機理，對礦產的勘探與開發有著重要的科學指導意義.

1 斑巖礦床巖體周圍容礦破裂的地質概況

前人對斑巖礦床的地質研究表明，絕大多數斑巖礦床都可以簡化為一個淺部的花崗巖侵入體侵入到以碳酸鹽巖和火山碎屑巖為主的圍巖中；侵入體被密集的網絡或網脈狀破裂系統所包圍，其頂部可能發育脈體和角礫巖筒；這些破裂是成礦流體運移和沉淀的重要場所，即成礦空間或容礦空間(圖1)(Kirkham and Sinclair,1995; Tosdal and Richards，2001; Guillou-Frottier and Burov，2003; Sillitoe,2010).如果以容礦破裂的類型來劃分斑巖礦床，可以劃分為兩個主要類型：脈體為主的斑巖礦床和角礫巖為主的斑巖礦床(Tosdal and Richards，2001；Guillou-Frottier and Burov，2003).脈體為主的斑巖礦床以圍繞深成巖體尖端的破裂、斷層和裂隙網絡為特征：在巖體頂部附近的脈體以及巖體頂部與圍巖接觸帶的網脈狀破裂系統中，通常發育較為高溫的銅礦和鐵礦，而距離巖體較遠的脈體中通常發育金、銀、鉛和鋅等溫度較低時形成的金屬礦物(圖1)(Sillitoe, 2010；Dilles and John，2021).脈體為主的斑巖礦床是較為常見的斑巖礦床類型，前人推測斑巖周圍網脈的形成與斑巖體的侵入、巖漿來源的熱液流體的出溶以及巖漿驅動的熱液系統冷卻過程有關(Tosdal and Richards，2001).在角礫巖為主的斑巖礦床中，含礦角礫巖為成礦前和成礦同時形成的角礫巖，其形狀由不規則狀到筒狀；這些角礫巖與圍巖呈突變或漸變的角度接觸，并且與斑巖侵入體有著密切聯系(圖1)(Tosdal and Richards，2001).角礫巖的基質組成為火成巖、熱液硅酸鹽和硫化物礦物，并且礦物的成分與斑巖礦床的蝕變分帶有良好的對應關系(Tosdal and Richards，2001；Sillitoe, 2010).前人認為斑巖礦床中的角礫巖形成與火成巖、巖漿-熱液和潛水巖漿作用有關(Tosdal and Richards，2001)，并且距離斑巖侵入體較近的角礫巖沒有明顯的方向性；前人推測這與孔隙流體超壓導致的巖石破裂有密切的聯系(Stephens et al., 2004；劉亮明，2011).成礦后期形成的角礫巖通常含礦較少(Sillitoe, 2010).

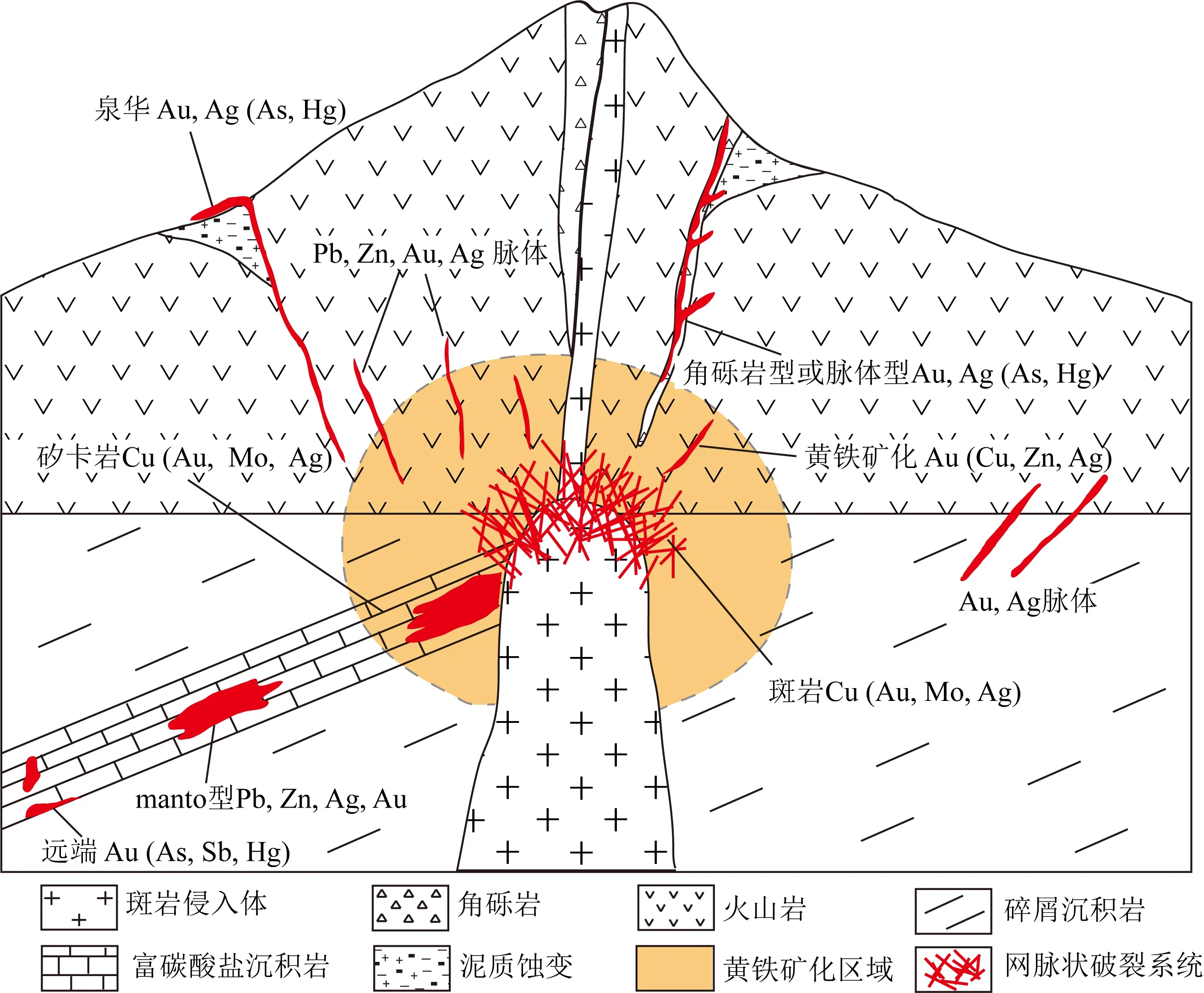
圖1 斑巖礦床中斑巖侵入體頂部破裂樣式和礦體類型示意圖.修改自Kirkham和Sinclair (1995) Fig.1 The schematic map of fracture styles and ore types at the top of porphyry intrusion in porphyry deposits. Modified from Kirkham and Sinclair (1995)

2 THM耦合方法及控制方程

2.1 孔隙介質力學

成礦過程是一種地質時間尺度的準靜態過程.因此，模型忽略了慣性力項，求解了靜力平衡方程(本研究中,壓應力為正，拉應力為負)：

σij,j-fi=0,

(1)

其中σij(i,j=x,y,z)為總應力張量在各個方向上的分量，fi為i方向上的體力(坐標軸定義見圖2a).在模型中，水平體力為0，垂直體力fy=ρmg，其中ρm為孔隙介質整體(固體顆粒骨架和孔隙流體)的平均密度，g為重力加速度(本研究中取9.81 m·s-2).孔隙介質的平均密度ρm可以表示為：

ρm=ρs(1-n)+ρfn,

(2)

其中ρs和ρf分別為固體顆粒和孔隙流體的密度，n為巖石體系的孔隙度.

本研究中的巖石材料均為線性飽和各向同性的孔隙介質材料，這種材料遵循有效應力原理(Terzaghi, 1925；Lade and Boer, 1997)：

σij=σ′ij+αpδij,

(3)

其中σ′ij(i,j=x,y,z)為有效應力張量在各方向的分量，有效應力是巖石固體骨架或巖石顆粒所承受的應力；p為孔隙流體壓力；δij為Kronecker delta函數(i=j,δij=1;i≠j,δij=0).α為Boit常數，α=1-K/Ks，K為孔隙介質整體的體積模量，Ks為固體骨架的體積模量.本研究中，巖石顆粒被假設為不可壓縮的，Ks的值趨向于無窮，所以Boit常數α=1(Thornton and Crook, 2014；Luo et al., 2015; Simulia, 2016).

耦合溫度場的孔隙介質力學本構方程可以表述為(Selvadurai and Nguyen, 1995；Atanackovic and Guran, 2000; Bai and Li, 2009)：

σij=2Gεij+λθδij+αpδij+3Kβs(T-T0)δij,

(4)

其中，

(5)

εij(i,j=x,y,z)為應力張量在各個方向上的分量，u為位移；θ為體應變，εx、εy和εz分別為對應下標表示的坐標軸方向的正應變；λ和G為Lame常數，K為孔隙介質整體的體積模量，E為楊氏模量，μ為泊松比；βs為固體顆粒的熱膨脹系數，T和T0分別為當前溫度和參考溫度(0 ℃).

本研究使用了Drucker-Prager塑性屈服準則(Drucker and Prager, 1952)：

(6)

其中，

(7)

I′1為有效應力張量的第一不變量，J2為偏應力張量的第二不變量，σ′1、σ′2和σ′3分別為最大有效主應力、中間有效主應力和最小有效主應力；σ′x、σ′y和σ′z分別為相應坐標軸方向的有效正應力，在本文的模型中，σ′x、σ′y和σ′z分別對應水平有效應力σ′h、垂直有效應力σ′v和平面外法向的有效應力σ′oop(坐標軸定義見圖2a)；τxy、τyz和τzx為對應平面內的剪應力，在本模型的平面應變假設下，只有τxy有值，其余剪應力分量為0.φ為內摩擦角；C為巖石顆粒的內聚力.

2.2 孔隙流體壓力的擴散方程(質量守恒)

本研究使用達西定律來模擬孔隙流體在巖石孔隙中的流動行為(Lewis and Schrefler, 1999; Craig, 2004; Simulia, 2016).達西定律可以表示為：

(8)

耦合了熱效應的孔隙介質質量守恒方程可以表示為(Bai and Li, 2009; Selvadurai and Najari, 2017)：

(9)

其中，

αT=3[nβf+(α-n)βs],

(10)

t為時間；α為Boit常數，αp和αT分別為孔隙流體壓力項和溫度項的耦合參數;Kf和βf分別為孔隙流體的體積模量和熱膨脹系數；n為巖石體系的孔隙度.

將公式(8)和(10)代入公式(9)，質量守恒方程可以表示為：

=0.

(11)

在本研究中，我們不考慮巖石顆粒和孔隙流體的可壓縮性，即巖石顆粒和孔隙流體為不可壓縮的，Ks和Kf均為無窮大，所以αp=0.

2.3 溫度擴散方程(能量守恒)

假設巖石顆粒的溫度和孔隙流體的溫度相等，那么巖石顆粒的能量守恒方程和孔隙流體的能量守恒方程可以分別表示為(Nield and Bejan, 2006)：

(12)

聯合公式(12)和(13)，可以得到孔隙介質整體的能量守恒方程(Nield and Bejan, 2006)：

(14)

其中，

(15)

最后，我們通過聯立靜力平衡方程(公式(1))、本構方程(公式(4))、幾何方程(公式(5)中第一個方程)、達西定律(公式(8))、質量守恒方程(公式(11))和能量守恒方程(公式(14))，來求解應力、應變、位移、孔隙流體壓力和溫度.在本構方程中，我們考慮了溫度和孔隙流體壓力的影響，在質量守恒方程中也同時考慮了溫度-孔隙流體壓力-應力應變的影響，在能量守恒方程中也考慮了孔隙流體熱對流作用的影響.本文使用了商業有限元軟件Abaqus求解上述方程組(Simulia, 2016)；該方程組是耦合在一起求解的，即本文的模型是全耦合的THM模型.

3 數值模型設置

本研究使用商業有限元軟件Abaqus(Simulia, 2016)，構建了一個概念性的、簡化的巖漿巖侵入體侵入到圍巖中的二維平面應變有限元模型(圖2a).該模型的時間步長由程序根據結果的收斂性自適應調整，時間步長的范圍從幾秒到幾十年.當模型結果的收斂性較好時，時間步長較長；當模型結果的收斂性較差時，時間步長較短(Simulia, 2016).該模型長6 km，高5 km，模型中央是一個筒狀的巖漿侵入體，頂部寬度約為500 m，侵入體與模型頂部表面之間的距離為1.5 km(圖2a).模型的剩余部分均為圍巖.

模型計算分為兩步.第一步為重力平衡步，經過這一步的計算，得到用于第二步THM耦合分析的初始應力場.這一步中，我們設置水平與垂直有效應力比K0為0.5，即：

(16)

模擬了重力平衡的應力場(Luo et al.,2015).第二步為THM耦合分析計算步，在這一步中，巖漿巖侵入體的初始溫度設為600 ℃，處于銅元素沉淀溫度與上地殼大型巖基溫度，即約550～700 ℃之間的范圍內(Sillitoe, 2010；Richards, 2011)；圍巖的初始溫度為頂部20 ℃，隨著深度的增加，溫度以25 ℃/km的地溫梯度增加，最終在模型底部達到170 ℃(圖2a).圍巖的初始孔隙流體壓力在頂部為1個大氣壓力(0.1 MPa)，在其余部分為靜水壓加上大氣壓(圖2a).對于邊界條件，在模型頂部，其溫度固定為20 ℃，其孔隙流體壓力固定為1個大氣壓力(0.1 MPa)，其法向和切向位移均自由；在模型兩側和底部，其溫度由模型表面溫度及地溫梯度計算得到(圖2a)，其孔隙流體壓力為靜水壓與大氣壓之和，其法向位移固定而切向位移自由.高溫侵入體及其周圍圍巖是此模型分析的重點區域，所以模型中間區域的網格較密(圖2a).

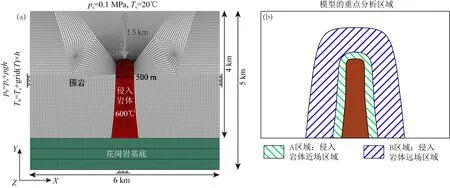
圖2 (a) 高溫柱狀巖體侵入到圍巖中的二維平面應變有限元模型的形狀、網格和邊界條件示意圖.其中，ps為地表孔隙流體壓力(大氣壓力)，Ts為地表溫度(20 ℃)，grid(T)為地溫梯度(25 ℃/km).(b)模型的重點分析區域.高溫巖體加熱圍巖所產生的應力應變擾動在侵入巖體近場區域(A區域)和侵入巖體遠場區域(B區域)有顯著的不同，所以本研究劃分了兩個不同的區域便于模型結果的描述Fig.2 (a) The model shape, meshes and boundary conditions of 2D plane strain finite element model for a high temperature columnar intrusion body intruding into the wall rock. Where, ps is the surface pore pressure (atmospheric pressure), Ts is the surface temperature (20 ℃), grid(T) is the underground temperature gradient (25 ℃/km). (b) The key analysis areas of this model. The perturbations of stresses and strains induced by the high temperature intrusion body heating wall rock have distinct differences in the zone near the intrusion body (zone A) and the zone far from the intrusion body (zone B), thus, we drew two different areas for the convenience of describing model results

前人研究表明，斑巖成礦系統的熱演化過程十分復雜，熔融巖漿的侵入過程以及斑巖礦床的形成過程伴隨著巖漿的多次或者持續的注入(Sillitoe,2010; Owen-Smith and Ashwal, 2015; Buret et al., 2016).為了簡化這種復雜的熱力學過程，本模型不考慮巖漿巖侵入的大變形過程，主要模擬高溫巖漿侵位完成之后侵入體加熱圍巖的物理場演化過程，并且在模擬持續時間內侵入巖漿始終保持600 ℃的高溫，來近似高溫巖漿的持續作用，直到孔隙熱彈塑性模型產生一定規模的破裂系統.我們選取模型模擬1000年時的結果作為最終結果，此時破裂已經達到了一定的規模.本研究的孔隙熱彈性模型與孔隙熱彈塑性模型的模擬時間一致.模型所用材料參數見表1.

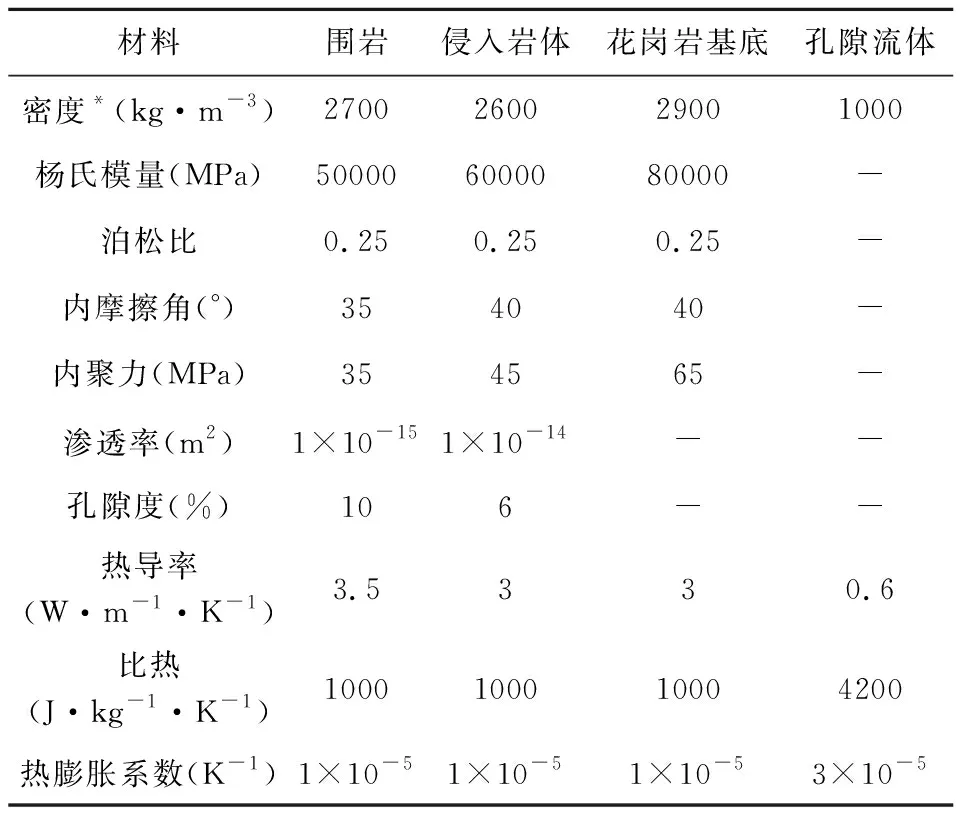
表1 柱狀巖體侵入圍巖概念模型的材料參數Table 1 The material properties for the conceptual model of columnar intrusion body intruding into the wall rock

4 模型結果

4.1 孔隙熱彈性模型結果與應力應變分析

我們首先分析了彈性模型中的力學狀態(圖3—圖7).彈性模型由于沒有塑性屈服，其偏應力結果可以無限增大(Luo et al., 2012)，因此，能夠計算高溫巖體的侵入對周圍圍巖應力應變的擾動.

在彈性模型結果中，高溫巖體加熱圍巖導致的應力應變狀態和擾動在靠近巖體的圍巖中(或巖體與圍巖的接觸帶中)和距離巖體較遠的圍巖中有明顯的不同,所以本研究劃分出了侵入巖體近場區域(圖2b中的A區域，可簡稱為近場區域)和侵入巖體遠場區域(圖2b中的B區域，可簡稱為遠場區域)作為兩個重點分析區域，使模型結果的描述更加清晰.

4.1.1 偏應力與平均應力的變化

模型初始的I1也隨深度線性增加(圖3b)，這與模型初始應力率一致(公式(16)).而高溫巖體侵入使得I1大大增加(圖3e)，在侵入巖體近場區域的巖體與圍巖的接觸帶位置，I1達到最大，約400～800 MPa(圖3e).因此，高溫巖體侵入導致I1在巖體與圍巖的接觸帶位置增加了約200～600 MPa(圖3h).

初始的孔隙流體壓力為大氣壓與靜水壓之和，其大小是隨深度線性增加的(圖3c).而高溫巖體侵入后，由于孔隙流體受熱膨脹，巖體內部和周圍圍巖中產生孔隙流體超壓，從而導致孔隙流體壓力增加(圖3f)，且距離侵入巖體越近，孔壓越大(圖3f).在侵入巖體周圍，孔壓增加約25～45 MPa，且在侵入巖體2至3倍幾何尺寸之外的位置，孔壓的擾動就完全消散了(圖3i).

4.1.2 有效主應力大小的變化

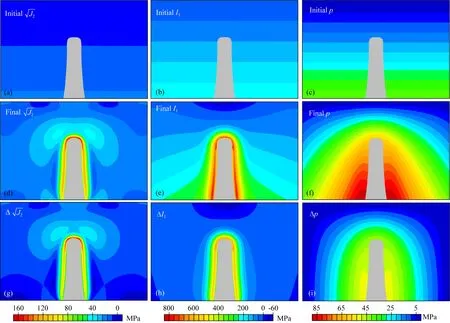
圖3 孔隙熱彈性模型的偏應力第二不變量總應力第一不變量I1和孔隙流體壓力p的初始值大小(a—c)、最終值大小(d—f)及其變化量(g—i).灰色部分為斑巖侵入體.每個色標對應其正上方的三張圖.對于I1和p的結果，擠壓為正，拉張為負Fig.3 The magnitudes of the second invariant of deviatoric stress tensor the first invariant of total stress tensor (I1), and the pore pressure (p) of the thermal-poroelastic model at the initial (a—c) and final modeling states (d—f), and their magnitude perturbations (g—i). The gray part is the porphyry intrusion body. Each color bar is corresponding to the figures that are right above it. The compression is positive and the extension is negative for I1 and p

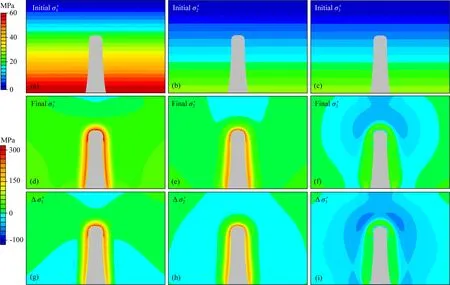
圖4 孔隙熱彈性模型的最大有效主應力(σ′1)、中間有效主應力(σ′2)和最小有效主應力(σ′3)的初始值大小(a—c)、最終值大小(d—f)及其變化量(g—i).灰色部分為斑巖侵入體.初始值共用上方的色標，最終值和變化量共用下方的色標.對于應力的符號，擠壓為正，拉張為負Fig.4 The magnitudes of the maximum effective principal stress (σ′1), the intermediate effective principal stress (σ′2) and the minimum effective principal stress (σ′3) of the thermal-poroelastic model at the initial (a—c) and final modeling states (d—f), and their magnitude perturbations (g—i). The gray part is the porphyry intrusion body. The upper color bar is corresponding to the initial states, and the lower color bar is corresponding to the final states and the perturbations. The compression is positive and the extension is negative for stress

4.1.3 有效正應力與主應力方向

在初始時刻，垂直有效應力(σ′v)是平面外法向的有效應力(σ′oop,垂直于平面的正向有效應力)和水平有效應力(σ′h)的兩倍，并且三者均隨深度線性增加(公式(16)；圖5a—5c).高溫巖漿巖體的侵入使得近場和遠場區域的三個有效正應力發生了很大變化(圖5d—5i).在侵入巖體近場區域(A區域，見圖2b)，高溫巖體的侵入使得σ′oop增加了約150～300 MPa(圖5g)：其增加量比σ′h和σ′v的增加量都要大(比較圖5g與圖5h、圖5i).最大有效主應力在近場區域中的方向是沿平面外法線方向的(圖6a)，所以靠近巖體的圍巖中的最大有效主應力是σ′oop.在近場區域，σ′h僅僅在巖體頂部圍巖的小范圍內大幅增加了約100～200 MPa，在巖體兩側的圍巖中增加量很小(圖5h)；而σ′v的變化則相反，在巖體頂部的圍巖中增加量很小，在巖體兩側的圍巖中大幅增加了約100～200 MPa(圖5i).從中間有效主應力的方向圖可以觀察到：在侵入巖體近場區域中，中間有效主應力的方向是沿著或平行于侵入巖體邊界的，即在巖體頂部接近水平方向，在巖體兩側接近垂直方向(圖6b).所以，在巖體頂部，中間有效主應力近似為σ′h，而在巖體兩側，中間有效主應力近似為σ′v.與中間有效主應力方向沿著侵入體邊界不同，在侵入巖體近場區域，最小有效主應力的方向是垂直于侵入巖體邊界的，即在巖體頂部接近垂直方向，在巖體兩側接近水平方向(圖6c).所以，在巖體頂部，最小有效主應力近似為σ′v，而在巖體兩側，最小有效主應力近似為σ′h.

在侵入巖體遠場區域(B區域，見圖2b)，水平有效應力(σ′h)在巖體上方減小約15～45 MPa(圖5h)，而垂直有效應力(σ′v)在巖體兩側減小約30～60 MPa(圖 5i).在侵入巖體遠場區域，巖體上方的最小有效主應力近似為水平有效應力，巖體兩側的最小有效主應力近似為垂直有效應力(圖6c).因此，在侵入巖體遠場區域，σ′h在巖體上方的減小以及σ′v在巖體兩側的減小，使得最小主應力的變化呈現拉張狀態(圖4i).

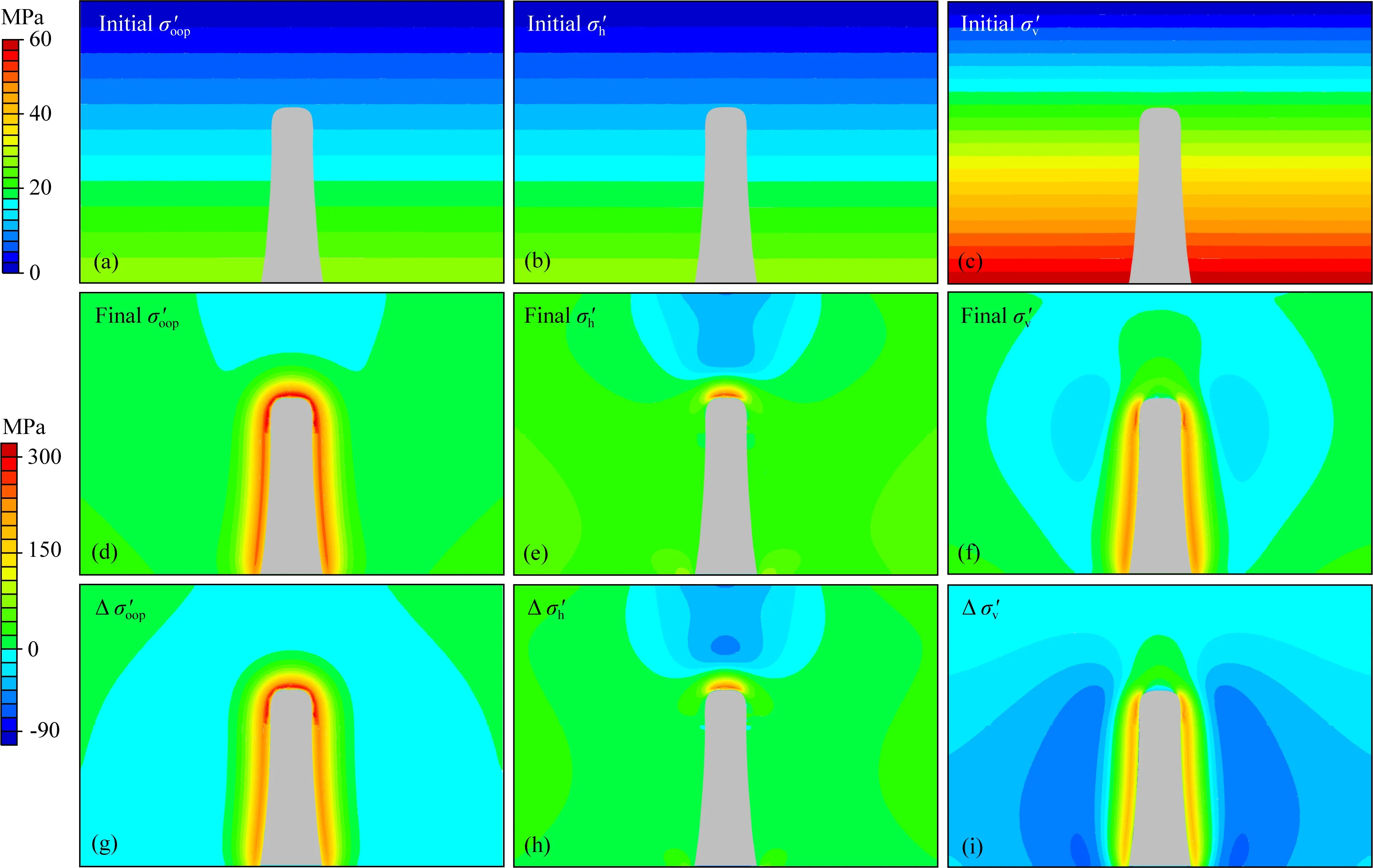
圖5 孔隙熱彈性模型的平面外法向有效應力(σ′oop)、水平有效應力(σ′h)和垂直有效應力(σ′v)的初始值大小(a—c)、最終值大小(d—f)及其變化量(g—i).灰色部分為斑巖侵入體.初始值共用上方的色標，最終值和變化量共用下方的色標.對于應力的符號，擠壓為正，拉張為負Fig.5 The magnitudes of the out-of-plane normal effective stress (σ′oop), the horizontal effective stress (σ′h) and the vertical effective stress (σ′v) of the thermal-poroelastic model at the initial (a—c) and final modeling states (d—f), and their magnitude perturbations (g—i). The gray part is the porphyry intrusion body. The upper color bar is corresponding to the initial states, and the lower color bar is corresponding to the final states and the perturbations. The compression is positive and the extension is negative for stress

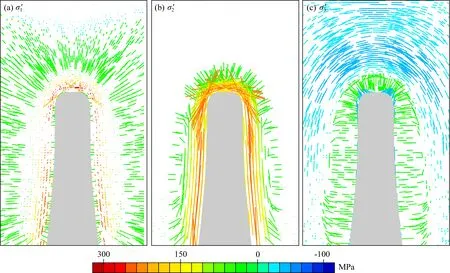
圖6 (a)(b)(c)分別為孔隙熱彈性模型的最大有效主應力(σ′1)、中間有效主應力(σ′2)和最小有效主應力(σ′3)的方向.灰色部分為斑巖侵入體.線段的顏色代表了有效主應力分量的大小.圖中的點表示該有效主應力方向是垂直于模型平面的Fig.6 (a), (b) and (c) are the directions of the maximum effective principal stress (σ′1), the intermediate effective principal stress (σ′2) and the minimum effective principal stress (σ′3) of the thermal-poroelastic model, respectively. The gray part is the porphyry intrusion body. The colors of the lines show the magnitudes of effective principal stress components. The points in this figure mean that the direction of the effective principal stress is normal to the model plane

4.1.4 溫度演化與應變的結果

整體來看，侵入巖體近場區域(A區域，見圖2b)的正應變以拉張應變為主，且應變值較高(圖7a—7c).而在侵入巖體遠場區域(B區域，見圖2b)，既有拉張應變也有擠壓應變，但拉張應變值遠大于擠壓應變值(圖7a—7c的色標).模型的溫度在初始時刻只有侵入體溫度較高(600 ℃)，圍巖的溫度隨地溫梯度變化(圖7d)；而在模擬的最后，侵入體近場區域的圍巖被加熱到了較高的溫度(200～500 ℃)(圖7e).

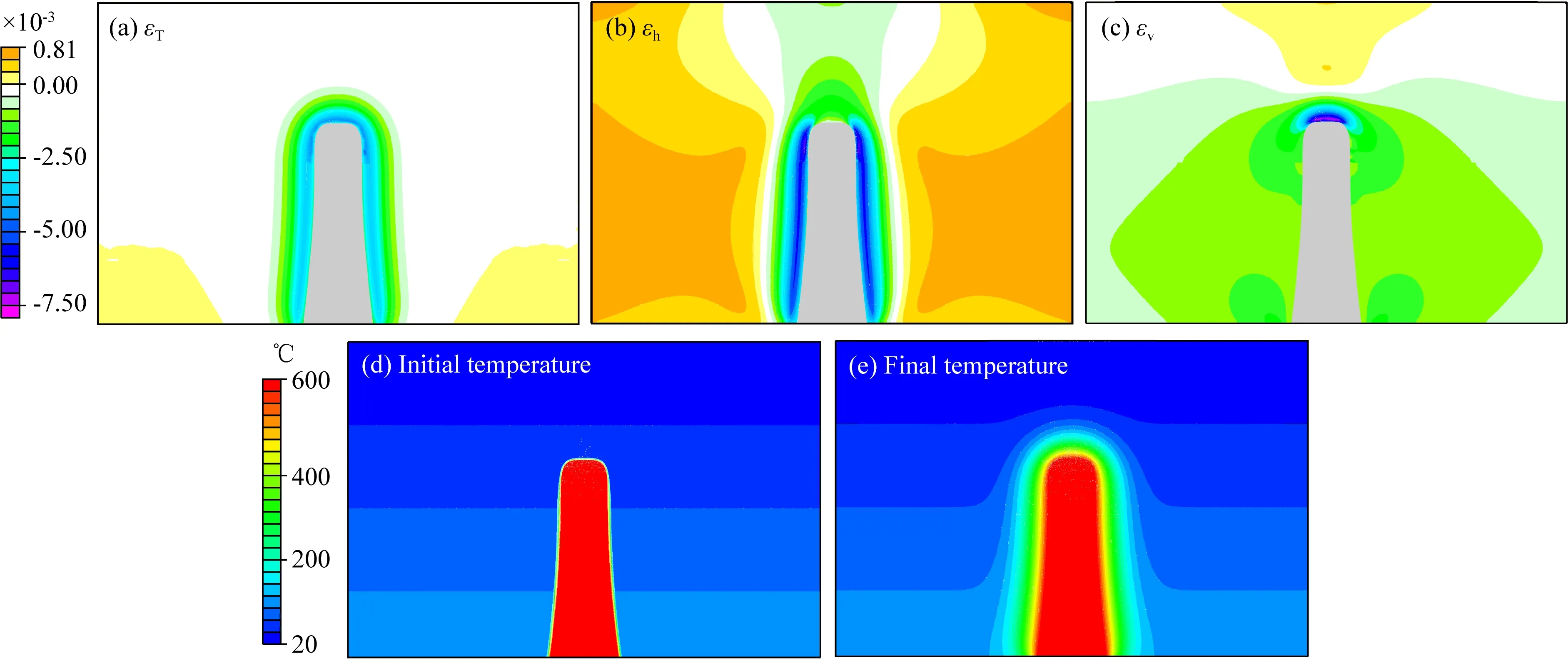
圖7 孔隙熱彈性模型中巖體的熱作用導致的(a)圍巖受熱膨脹產生的應變(熱應變εT)、(b)水平應變(εh)和(c)垂直應變(εv)的分布.灰色部分為斑巖侵入體.正應變和熱應變以縮短(擠壓)為正，伸長(拉張)為負.由于模型的平面應變假設，平面外法向的正應變為0.(d—e)孔隙熱彈性模型的溫度演化結果Fig.7 The distributions of (a) thermal strain (εT), (b) horizontal strain (εh) and (c) vertical strain (εv) induced by the heating effect of intrusion body in the thermal-poroelastic model. The gray part is the porphyry intrusion body. The shorten (compressive) strain is positive and the extension (tensile) strain is negative. The out-of-plane normal strain equals zero because of the plane strain hypothesis of this model. (d—e) The results of temperature evolution in the thermal-poroelastic model

高溫侵入巖體加熱圍巖使得圍巖受熱膨脹(圖7e)，產生熱應變(εT)(圖7a).在侵入巖體近場區域(A區域，見圖2b)，距離巖體較近的圍巖被加熱到較高的溫度(圖7e)，因此越靠近侵入巖體的圍巖熱應變(熱膨脹)就越大(圖7a).而在侵入巖體遠場區域(B區域，見圖2b)，圍巖沒有受到高溫侵入巖體的加熱(圖7e)，所以遠場區域的熱應變為0(圖7a).

在侵入巖體近場區域(A區域，見圖2b)，水平應變(εh)在巖體兩側的拉張最大(見圖7b藍色位置)，可達-0.0025至-0.0075，而εh在巖體頂部的拉張較小，僅為-0.001至-0.0025(圖7b).在侵入巖體遠場區域(B區域，見圖2b)，εh只在巖體的頂部有一些拉張應變(見圖7b侵入體上方的淺綠色區域)，約為0至-0.00125，而在巖體的兩側呈很小的擠壓應變(圖7b).

在侵入巖體近場區域(A區域，見圖2b)，垂直應變(εv)在巖體頂部的拉張最大(見圖7c藍色位置)，可達-0.0025至-0.0075，而εv在巖體兩側的拉張較小，僅為-0.001至-0.0025(圖7c).在侵入巖體遠場區域(B區域，見圖2b)，εv在巖體的頂部呈很小的擠壓應變，而在巖體的兩側為拉張應變，約為-0.0004至-0.00125(見圖7c侵入體兩側的淺綠色區域).

4.1.5 利用應變解釋正應力的分布

對比應變的結果和三個正應力的結果可以發現，在侵入巖體近場區域，三個正應力(σ′oop、σ′h和σ′v)都是擠壓應力(圖5g—5i)，但是應變分量(εT、εh和εv)卻是拉張應變(圖7a—7c)；而在侵入巖體遠場區域，拉張的應力又能對應拉張的應變(對比圖5h和圖7b，對比圖5i和圖7c).導致這種現象的原因是近場的圍巖受熱膨脹產生了拉張的熱應變，但是遠場的圍巖沒有受熱膨脹，所以遠場圍巖會擠壓并約束近場圍巖的熱膨脹作用，導致近場的圍巖中產生了擠壓的熱應力，而遠場的圍巖由于沒有被加熱所以沒有受到這種擠壓約束作用.根據孔隙熱彈性的本構方程(公式(4))，我們能更具體地看到熱應變產生的擠壓作用.展開公式(4)，可得到平面應變孔隙熱彈性(本文簡稱彈性模型)本構方程的各個分量：

σ′oop=λ(εh+εv)-3KεT,

σ′h=λ(εh+εv)+2Gεh-3KεT,

σ′v=λ(εh+εv)+2Gεv-3KεT,

τxy=2Gεxy,

εT=-βs(T-T0) ,

(17)

其中，εh、εv和εxy分別為水平應變、垂直應變和平面內剪應變，εT為熱應變(由于規定擠壓應變為正，拉張應變為負，而熱膨脹為拉張應變，為了統一應變的符號，本文在熱應變的表達式前加了負號).從公式(17)可以注意到，εh、εv與應力呈正相關，表明了彈性應力與應變的對應關系；而εT與應力呈負相關，表明拉張的εT會產生擠壓應力.

基于上述的熱應變(或熱膨脹)與應力的負相關關系，根據公式(17)，利用熱應變(εT)、水平應變(εh)以及垂直應變(εv)的分布，可以分析和解釋平面外法向有效應力(σ′oop)、水平有效應力(σ′h)和垂直有效應力(σ′v)的變化或擾動.具體分析和解釋如下：

對于平面外法向有效應力(σ′oop)，在侵入巖體近場區域，巖體兩側的水平應變(εh)和巖體頂部的垂直應變(εv)的拉張較大(圖7b和7c)，所以λ(εh+εv)這一項所產生的應力是圍繞巖體的拉張應力(公式(17))；靠近巖體的圍巖熱膨脹產生拉張的熱應變(εT)(圖7a)，而εT導致的擠壓應力的作用(-3KεT)大于λ(εh+εv)所產生的拉張應力，所以σ′oop的擠壓應力增加量在近場區域中三個方向的正應力中最大(圖5g)(公式(17)).

對于水平有效應力(σ′h)，根據公式(17)，與平面外法向有效應力(σ′oop)相比，σ′h的方程中多了2Gεh這一項，所以σ′h的擾動與σ′oop的擾動之間的差異主要受到εh的控制.在侵入巖體近場區域(A區域，見圖2b)的巖體兩側，εh的拉張很大(圖7b中藍色區域)，其產生的拉張應力抵消了εT產生的擠壓應力(圖7a與圖5g)，所以σ′h的增加量很小(圖5h)；而在近場區域的巖體頂部，εh的拉張較小(圖7b)，εT產生的擠壓應力(圖7a與圖5g)只有小部分被抵消，所以σ′h有較大的擠壓應力的增加(圖5h中黃色和紅色區域).在侵入巖體遠場區域(B區域，見圖2b)，εT的作用較小(圖7a)，εh在巖體頂部為拉張應變(圖7b中巖體頂部淺綠色區域)，所以相比于σ′oop的擾動(圖5g)，σ′h在遠場區域的巖體頂部有明顯的拉張應力的增加(圖5h中藍色區域).

同理，對于垂直有效應力(σ′v)，根據公式(17)，與σ′oop相比，σ′v的方程中多了2Gεv這一項，所以σ′v的擾動與σ′oop的擾動之間的差異主要受到εv的控制.在侵入巖體近場區域(A區域，見圖2b)的巖體頂部，εv的拉張很大(圖7c中藍色區域)，其產生的拉張應力抵消了εT產生的擠壓應力(圖7a與圖5g)，所以σ′v的增加量很小(圖5i)；εv在近場區域巖體兩側的拉張較小(圖7c中綠色區域)，εT產生的擠壓應力(圖7a與圖5g)只有小部分被抵消，所以σ′v有較大的擠壓應力的增加(圖5i中黃色和紅色區域).而在侵入巖體遠場區域(B區域，見圖2b)，εT的作用很小(圖7a)，εv在巖體兩側為拉張應變(圖7c中綠色區域)，所以相比于σ′oop的擾動(圖5g)，σ′v在遠場區域的巖體兩側有明顯的拉張應力的增加(圖5i中藍色區域).

4.2 孔隙熱彈塑性模型的應力應變結果

我們在上述孔隙熱彈性模型中加入了塑性，使用了Drucker-Prager塑性屈服準則，來模擬由高溫巖體侵入導致的等效塑性應變(即破裂)的形成，并分析了偏應力、平均應力及孔隙流體壓力對破裂形成與發育的控制影響作用(圖8).孔隙熱彈塑性模型結果顯示，演化過程的早期(200年)，破裂首先在近場區域(A區域，見圖2b)侵入體與圍巖的接觸帶中發育(圖8a)；演化過程的中期(500年)，侵入體與圍巖接觸帶中的破裂繼續發育，而侵入體上部開始發育脈狀破裂(圖8b)；演化過程的晚期(1000年)，在侵入巖體遠場區域(B區域，見圖2b)中巖體頂部的側上方發育了大中型脈狀破裂系統，且破裂距離巖體中軸越遠，其傾角越小：靠近巖體中軸的破裂傾角約為80°到90°，而距離巖體中軸較遠處破裂傾角減小至約60°(圖8c).

我們選取了新形成的破裂上的一點(圖8c中點C)，通過分析這一點的偏應力、平均應力、孔隙流體壓力及塑性屈服準則中各項的值隨時間的演化，來探討破裂形成的力學過程(圖8d).將公式(6)中的I′1展開，可得

(18)

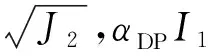
4.3 不同侵入體溫度的對比模型形成的破裂規模

在本文的孔隙熱彈塑性模型中，侵入體的溫度是重要的邊界條件.前人的地質研究表明，在斑巖銅成礦系統中，銅元素沉淀的主要階段的溫度范圍是550 ℃到350 ℃(Sillitoe, 2010).并且，濕花崗巖的固相線約為700 ℃，而上地殼的大型巖基的溫度大于700 ℃(Richards, 2011).所以斑巖成礦系統的侵入體溫度要大于銅元素沉淀的主要階段的溫度，還要小于上地殼巖基的溫度，即約550 ℃到700 ℃.因此，我們給定的侵入體溫度也處于這個范圍之中.此外，為了研究侵入體的溫度值對于破裂系統形成的影響，為斑巖成礦系統的侵入體溫度的下限提供約束，我們設置了兩個孔隙熱彈塑性模型的對比模型，僅改變孔隙熱彈塑性模型的侵入體溫度，兩個對比模型中侵入體的溫度分別為500 ℃和400 ℃(圖9).對比模型的演化時間和侵入體為600 ℃模型的演化時間一致(約1000年).

模型結果顯示，侵入體為500 ℃時，近場區域侵入體的頂部發育了一些破裂，但是遠場區域中侵入體上部只有兩簇很小的破裂(圖9a)，遠沒有600 ℃模型遠場區域的放射狀破裂系統發育(圖8c)；當侵入體溫度為400 ℃時，侵入體周圍的破裂幾乎不發育(圖9b).所以，模擬結果表明，當侵入體的溫度大于500 ℃時，侵入體頂部才能形成小規模的容礦破裂，這樣就約束了斑巖成礦系統的破裂形成過程中侵入體溫度的下限.而當侵入體溫度達到600 ℃時，侵入體頂部能夠形成較大規模的破裂系統(圖8c).模擬結果得出的溫度范圍與地質實際具有一致性，為侵入體溫度范圍和容礦破裂形成的溫度提供了物理力學的約束.

圖8 (a—c)孔隙熱彈塑性模型中等效塑性應變(破裂)的演化結果.灰色部分為斑巖侵入體.(d)巖體側上部脈狀破裂中一點C(圖8c)的塑性屈服準則中各項及等效塑性應變隨時間的變化曲線.(e)巖體頂部與圍巖接觸帶的破裂中一點D(圖8c)的塑性屈服準則中各項及等效塑性應變隨時間的變化曲線Fig.8 (a—c) The result of the equivalent plastic strain evolution of the thermal-poroelastoplastic model. The gray part is the porphyry intrusion body. (d) The time-varying plots of the terms in the plastic yield criterion and the equivalent plastic strain for the point C (Fig.8c) within the vein-shaped fractures above the intrusion body. (e) The time-varying plots of the terms in the plastic yield criterion and the equivalent plastic strain for the point D (Fig.8c) within the fractures at the contact zone between the intrusion body and wall rock

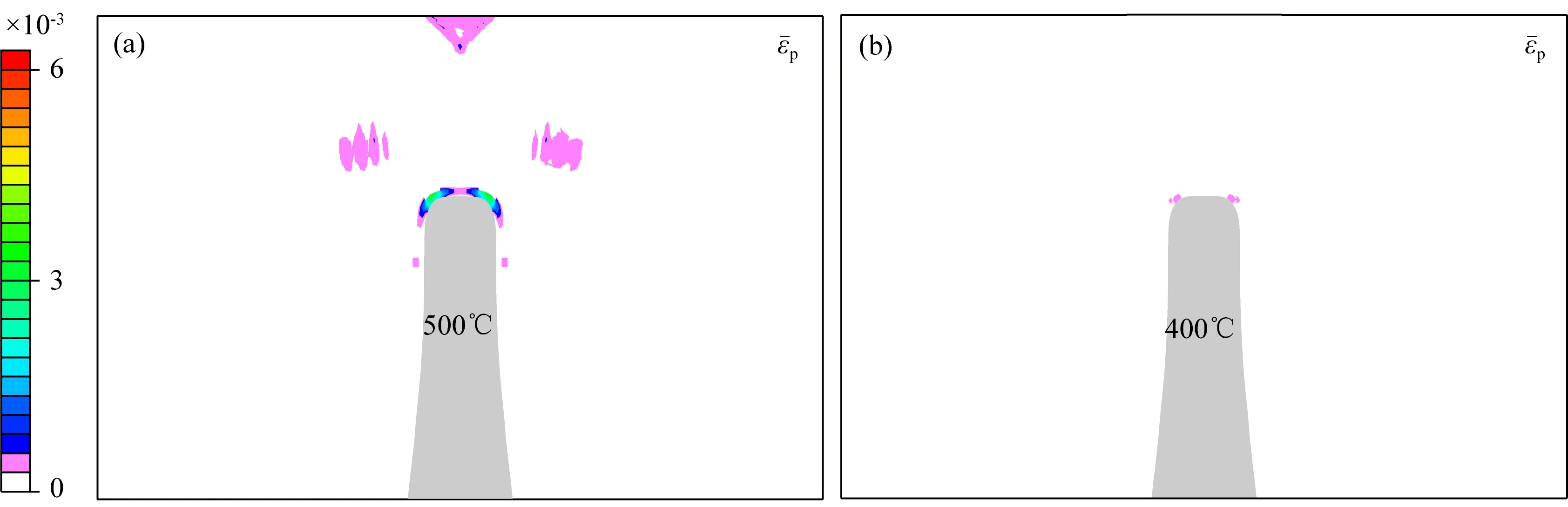
圖9 (a)侵入體溫度為500 ℃時，孔隙熱彈塑性模型中的等效塑性應變結果.(b)侵入體溫度為400 ℃時，孔隙熱彈塑性模型中的等效塑性應變結果Fig.9 (a) The results of equivalent plastic strain in the thermal-poroelastoplastic model, in which the temperature of intrusion is 500 ℃. (b) The results of equivalent plastic strain in the thermal-poroelastoplastic model, in which the temperature of intrusion is 400 ℃

5 青藏甲瑪斑巖礦床數值模擬

為了將本文的概念模型運用到實際礦床中，我們以青藏甲瑪斑巖銅多金屬礦床為例，建立了孔隙熱彈塑性有限元模型，計算探討了侵入巖體頂部圍巖中的破裂樣式，并與甲瑪礦床實際地質觀察進行了比較分析(圖10).

5.1 甲瑪礦床地質簡述

甲瑪斑巖銅多金屬礦床位于特提斯—喜馬拉雅成礦域的西藏岡底斯成礦帶，該成礦帶以中特提斯班公—怒江縫合帶和新特提斯印度—雅魯藏布縫合帶為邊界，在東西方向長約2000 km，在南北方向寬約500 km(楊德明等, 2001; Hou and Cook, 2009; Hou et al., 2015).前人研究表明，岡底斯成礦帶經歷了復雜的地質和地球動力學歷史，包括雅魯藏布新特提斯洋的俯沖-后撤-碰撞過程以及印度板塊和拉薩地體的碰撞過程(Pan et al., 2012; Mao et al., 2014; Wang et al., 2015).甲瑪斑巖銅多金屬礦床形成于中新世印度板塊與拉薩板塊碰撞的后碰撞伸展階段(約20～12 Ma)，主要由四種礦體組成(圖10a)：(1)斑巖銅-鉬礦體，賦存于斑巖侵入體內部及其周圍圍巖的網脈狀破裂系統中，以浸染狀和脈狀的黃銅礦為主；(2)層狀和似層狀的矽卡巖銅-多金屬礦體，賦存于上覆的林步宗組砂巖-板巖和下層多地溝組灰巖-大理巖的層間剝離帶中；(3)角巖銅-鉬±金±銀礦體，主要以脈狀賦存于斑巖體頂部的角巖破裂系統和節理系統中；(4)淺成熱液金銀礦體，主要賦存于巖體外圍的破裂和閃長玢巖中(冷秋鋒等, 2015; Zheng et al., 2016; 林彬等, 2019).

5.2 甲瑪礦床有限元模型設置及結果

本文建立的甲瑪礦床模型為二維平面應變孔隙熱彈塑性有限元模型(即前文中的彈塑性模型)，模型高6 km，寬8 km(圖10b).模型中的地層形狀與甲瑪礦床的實際地層分布基本一致(圖10a和10b).模型的初始條件和邊界條件的設置與柱狀巖體侵入圍巖的概念模型一致(圖10b).初始的孔隙流體壓力在模型頂部為大氣壓(0.1 MPa)，其余深度的初始孔隙流體壓力為大氣壓力與靜水壓力之和；初始溫度在模型頂部為室溫(20 ℃)，其余深度的溫度按照地溫梯度(25 ℃/km)增加；孔隙流體壓力邊界為頂部大氣壓，兩側和底部為大氣壓力與靜水壓力之和；溫度邊界為頂部室溫，兩側和底部按照地溫梯度增加，巖漿房的溫度維持在700 ℃，也處于銅元素沉淀溫度與上地殼大型巖基溫度，即約550～700 ℃之間的范圍(Sillitoe, 2010；Richards, 2011)；位移邊界條件為頂部法向和切向位移自由，兩側和底部為法向位移固定、切向位移自由(圖10b).模型所用材料參數見表2.

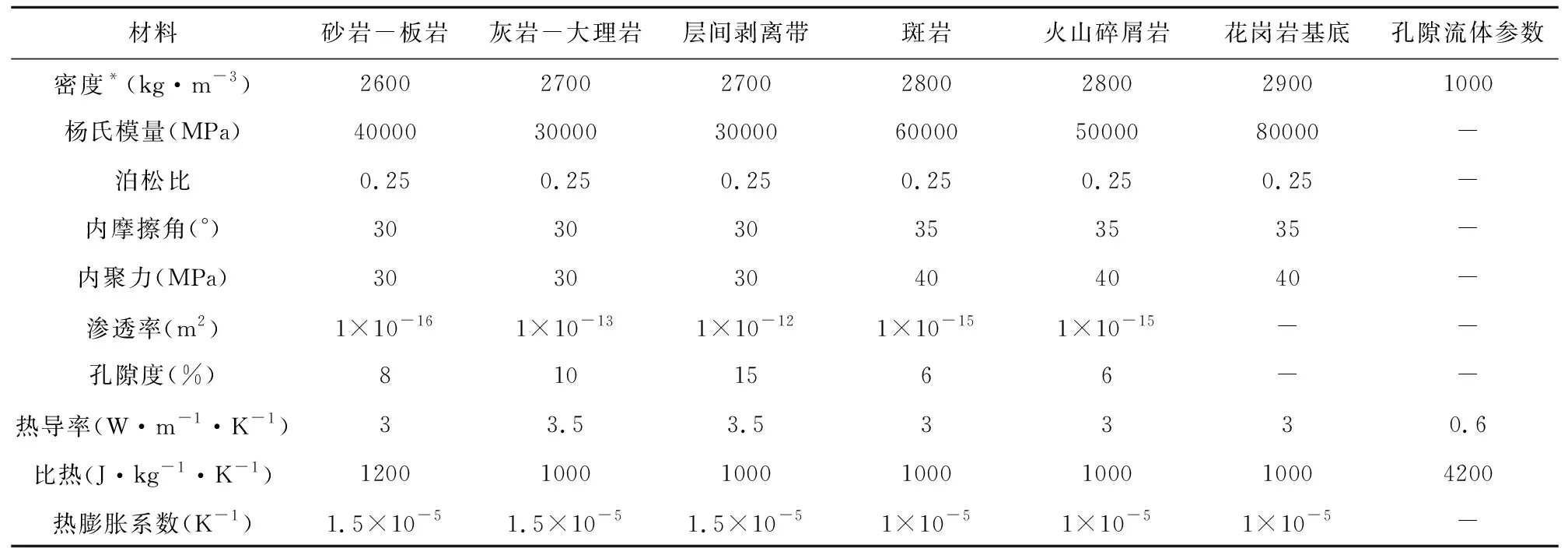
表2 甲瑪礦床模型的材料參數Table 2 The material properties for the Jiama deposit model

甲瑪礦床有限元模型的結果顯示，斑巖侵入體頂部形成并發育了豐富的破裂系統.從侵入巖體頂部的兩個凸起開始，向外發育了傾角不同的多個破裂，巖體頂部與圍巖的接觸帶也發育了圍繞巖體邊界的破裂(圖10c)，形成了甲瑪礦床的流體通道、導礦構造及容礦空間.這些模擬的破裂帶位置與甲瑪礦床斑巖體頂部賦存斑巖礦體和角巖礦體的破裂系統對應很好(圖10a和10c).我們的數值模擬研究從力學角度在一定程度上解釋了侵入巖體頂部破裂的形成與發育，并且為地學工作者暗示了甲瑪礦床的流體通道、導礦構造及容礦空間的位置及區域.

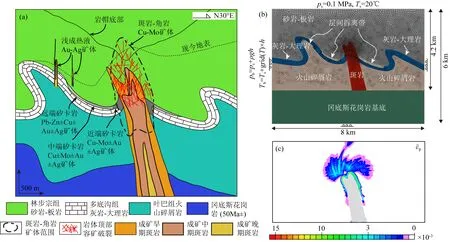
圖10 (a)甲瑪礦床地質剖面圖，顯示了不同種類的礦體在空間上的分布，以及破裂對于斑巖和角巖礦體的控制作用.修改自Zheng 等 (2016).(b)甲瑪礦床二維平面應變孔隙熱彈塑性有限元模型的形狀、網格以及邊界條件示意圖.其中，ps為地表孔隙流體壓力(大氣壓力)，Ts為地表溫度(20 ℃)，grid(T)為地溫梯度(25 ℃/km).(c)甲瑪礦床模型計算得到的巖體頂部等效塑性應變的分布.灰色部分為斑巖侵入體Fig.10 (a) The geological section map of Jiama deposit, showing the spatial distributions of different ore body types and the controlling effect of fractures on the porphyry and hornfels ore bodies. Modified from Zheng et al., 2016. (b) The model shape, meshes and boundary conditions of 2D plane strain thermal-poroelastoplastic finite element model for Jiama deposit. Where, ps is the surface pore pressure (atmospheric pressure), Ts is the surface temperature (20 ℃), grid(T) is the underground temperature gradient (25 ℃/km). (c) The distribution of the equivalent plastic strain at the top of the intrusion body calculated by the Jiama deposit model. The gray part is the porphyry intrusion body

6 討論

斑巖礦床的形成是以幔源巖漿侵入為前提的，而地幔巖漿的上涌需要板塊的俯沖和碰撞等作用來形成深大斷裂，為巖漿的上侵提供通道(Tosdal and Richards, 2001; Richards, 2003).因此，前人對于高溫巖漿侵入體周圍破裂形成力學機制的數值模擬，大多都包含擠壓或者拉張的構造應力背景，從而來研究構造應力或構造運動導致的深大斷裂或斷層的形成與發育(Guillou-Frottier and Burov,2003; Zhang et al.,2012).但是，這些大斷層的發育時間通常都為幾十萬年甚至幾個百萬年，與斑巖礦床巖體頂部或上部的破裂系統生成的時間尺度存在差異.另外，這些大斷層通常切穿地殼并向上延伸至地表，與小區域的、礦田尺度的斑巖礦床巖體頂部的網脈破裂和上部的脈狀破裂，在空間尺度上存在很大差異(圖1).這些研究通常沒有考慮巖漿侵入且加熱圍巖導致破裂形成的力學機理(Guillou-Frottier and Burov,2003; Zhang et al.,2012).

前人對于斑巖成礦系統的研究表明，斑巖礦床的經濟礦體大多產于熱液系統演化早期形成的構造和蝕變帶中(Sillitoe，2010；Dilles and John，2021)，且在巖漿系統到熱液系統的過渡過程中，含礦熱液流體能以很快的速度進入巖體周圍的破裂系統中，進而析出沉淀形成礦體(Launay et al., 2018).考慮到以上因素及前人的研究，本文的模型沒有包含構造應力或構造運動的作用，而是聚焦研究了高溫巖體侵入后對其周圍圍巖的加熱作用及其相關的破裂形成過程.模型結果顯示，模擬到約1000年時巖體頂部就出現了具有一定規模的脈狀破裂系統(圖8c).這些結果表明斑巖侵入體頂部的容礦破裂系統的形成過程可能比地質上認為的時間要短得多，大約僅為千年尺度.

斑巖礦床巖體周圍的容礦破裂主要分為兩種，一種是巖體頂部圍巖接觸帶中的網脈狀破裂系統，這種破裂的單個破裂規模較小，但是分布密度較大，形成密集的容礦網脈，主要賦存斑巖型銅±鉬礦體；另一種是巖體頂部上方具有一定規模的大中型脈體和角礫巖筒，以巖體頂部為中心，呈放射狀向上方或斜上方延伸，距離斑巖侵入體較近的脈體賦存斑巖銅(金銀鋅)礦體或者角巖銅±鉬礦體，距離侵入體較遠的脈體賦存較低溫度下形成的鉛鋅金銀礦體(圖1；Kirkham and Sinclair,1995；Guillou-Frottier and Burov，2003；Sillitoe，2010；Zheng et al., 2016).本文的孔隙熱彈性模型模擬了高溫巖體的侵入對周圍圍巖產生的應力應變擾動，闡述了高溫侵入體加熱圍巖產生偏應力集中的原因(圖3—圖7)；而在孔隙熱彈塑性模型中，模擬出了巖體頂部近似放射狀的大中型脈狀破裂以及巖體與圍巖接觸帶中的破裂，并且分別對兩種破裂進行了應力及孔隙流體壓力演化分析.這些結果表明，對于具有較高滲透率頂層的斑巖成礦系統，高溫巖體侵入圍巖的熱作用導致的偏應力集中是侵入巖體頂部破裂系統形成的主要原因(圖3d,3g,8d和8e)，而孔隙流體壓力對這些破裂形成也具有一定的輔助作用(圖8d和8e).模型模擬的破裂結果與地質上巖體頂部的兩種不同類型容礦破裂有較好的一致性，能夠從地質力學的角度解釋巖體頂部破裂形成機制，為斑巖礦床找礦勘探提供一定的指導作用.

本文的模型沒有考慮巖漿侵入體侵入到圍巖中的大變形過程，因為這一過程十分復雜，包含了多種物理力學和化學反應機制(Sillitoe，2010；Richards，2013).前人對于這種侵入過程的力學作用有過簡單的研究，研究方法包括對模型底部施加不均勻的壓力邊界條件(Hafner，1951)，以及對巖漿侵入體頂部施加向上的侵入壓力(Koide and Bhattacharji，1975；Sartoris et al，1990)，所得到的結果都表明巖漿侵入體的侵入壓力對于巖體頂部的破裂發生和發育具有重要作用.本文沒有考慮這種侵入壓力的作用，而是聚焦于高溫巖漿對圍巖的熱作用，但是能夠推測，巖體侵入壓力的加入會促進本研究模型中巖體頂部破裂的發生和發育.

本文通過熱-流體-應力應變耦合(THM耦合)的有限元模型，重點研究了高溫巖體加熱圍巖導致偏應力在巖體頂部集中的原因，及其導致的巖體頂部破裂系統的力學演化過程.本研究的模型并沒有模擬真實的巖石開裂、流體充填、礦物析出沉淀等地質過程，因為這些過程的物理力學非常復雜，不容易模擬，模型計算也不容易收斂.本文的模型也沒有考慮侵入體的流體壓力、流體相分離以及流體參數隨溫度壓力的變化等因素的影響.我們強調，本文的模型是對斑巖熱液成礦系統的一階近似，通過耦合熱-流體-力學(THM耦合)，來研究侵入體周圍破裂形成的基本物理過程，為容礦空間的形成提供基本的力學機制解釋，是向著開發更復雜、更現實的成礦過程物理模型邁出的第一步.考慮上述更現實的地質過程和因素的影響，超出了本文的研究內容，但可作為未來的研究內容和方向.

7 結論

本文開發了一套新的高溫斑巖侵入體加熱圍巖并產生破裂的熱-流體-應力應變耦合的二維平面應變有限元數值模型，研究了斑巖成礦系統頂部破裂帶形成與發育的力學機制及過程.首先建立了一個簡化的、概念性的柱狀巖漿侵入體加熱圍巖的二維孔隙熱彈性平面應變有限元模型，分析了高溫巖漿的熱作用對其圍巖的應力應變擾動和破裂形成機制.近一步，在這個彈性模型中加入塑性，計算了斑巖成礦系統的應力應變，調查了巖體頂部破裂形成和發育的力學演化過程.最后，依據青藏甲瑪斑巖礦床的地質、地層數據及信息，建立了更加實際的甲瑪斑巖礦床成礦系統模型，計算了巖體頂部破裂的形成與發育，模擬結果與實際地質情況一致，從而為深部找礦勘探工作提供了科學指導.基于以上研究工作，本文的研究結論主要有如下幾點：

(1)高溫柱狀侵入巖體加熱了其周邊圍巖，對這些圍巖施加了附加的變形：在侵入巖體近場區域，水平應變在侵入巖體兩側拉張較大，在侵入巖體頂部拉張較小；垂直應變在侵入巖體頂部拉張較大，在侵入巖體兩側拉張較小.在侵入巖體遠場區域，巖體上部的水平應變和巖體兩側的垂直應變為拉張應變.巖體與圍巖的接觸帶受熱膨脹產生了拉張的熱應變.

(2)高溫柱狀侵入巖體加熱圍巖導致了侵入巖體頂部以及侵入巖體與圍巖接觸帶中三個主應力的增加和減小的幅度不同，從而在侵入巖體頂部以及侵入巖體與圍巖接觸帶中形成了差應力或偏應力的集中.

(3)對于具有較高滲透率頂層的斑巖成礦系統，高溫巖體侵入圍巖的熱作用導致的偏應力集中是侵入巖體頂部破裂系統以及侵入巖體與圍巖接觸帶中破裂形成與發育的主要原因，而孔隙流體壓力對這些破裂形成與演化也具有一定的輔助作用.

致謝感謝審稿專家的建設性意見以及編輯部的大力支持.