采用觀測氣隙的電磁吸力懸浮系統研究*
張曉宇, 劉國清, 董金文, 吳 桐
(西南交通大學 電氣工程學院,四川 成都 610097)
0 引 言
磁懸浮是指通過電磁鐵或者永磁體產生的磁場作用到懸浮物體上,使得物體的重力與磁場產生的斥力或者吸力達到平衡,從而實現物體懸浮。隨著技術的不斷進步,磁懸浮的應用領域不再局限于懸浮列車,在工業生產領域與生命科學領域也得到應用[1]。如磁懸浮軸承[2]、磁懸浮熔煉[3]和磁浮人工心臟泵[4]等。
單自由度懸浮系統有結構簡單、數學模型明確、控制性能直觀、研發周期短的優點[5]。開環單自由度懸浮系統主要包括電流傳感裝置、懸浮體、控制電路、電磁鐵等。當電磁鐵通入電流時,懸浮體會在電磁鐵產生的磁場的作用下受到與重力相反的力;不斷調節電流的大小,可使懸浮體實現穩定的懸浮。
當懸浮體受到外界擾動時,可能使懸浮體產生過大的位移偏離從而導致電磁力突然變化,失去與重力的平衡,從而不能達到懸浮。為了使懸浮體在外界擾動下仍具有良好的懸浮能力,往往要引入氣隙傳感器作為反饋從而實現閉環控制[6]。氣隙的精確采集對懸浮體穩定懸浮尤為重要,而傳統的氣隙采集方式對氣隙傳感器精度的要求高,且造價昂貴、體積大、安裝復雜。若采用無氣隙傳感器的反饋方式,不僅能簡化系統、降低成本,同時也能減少由于傳感器測量不穩定而導致懸浮控制系統不穩定的風險,從而提高懸浮可靠性。
當前無氣隙傳感器的懸浮控制研究主要集中在狀態估計法和參數辨識法上[7]。狀態估計法是選取特定的物理量作為觀測量、狀態量和控制量。傳統的狀態估計法選取位置信息、電流大小以及線圈電壓分別作為狀態量、觀測量和控制量。文獻[8]引入了狀態觀測器。考慮到外界對懸浮體的擾動,文獻[9]采用了混合狀態觀測器,這種方法去除了降維電流觀測器和外力觀測器。文獻[10]采用的高頻小信號測試法所測量的激勵值過大或者過小,容易導致控制效果不精確。
本文以單自由度懸浮系統為研究對象,提出了一種基于磁場和電流觀測氣隙,使用觀測氣隙進行閉環反饋的電磁吸力懸浮方法,可實現懸浮控制。分析了氣隙與磁場和電流之間的函數關系,對氣隙觀測函數進行擬合,并分析了氣隙函數中的參數對閉環系統穩定性的影響,最終應用觀測氣隙方法實現了懸浮物在無氣隙傳感器條件下的懸浮。
1 電磁吸力懸浮系統電磁場懸浮理論分析
在單自由度電磁吸力懸浮系統中,懸浮物分為永磁體與導磁體。本文以后者作為懸浮物,搭建了電磁吸力懸浮模型。
考慮到電磁鐵工作時產生的漏磁較大,為單自由度電磁吸力懸浮系統增加了金屬外殼以減少漏磁。單自由度電磁吸力懸浮系統模型如圖1所示。
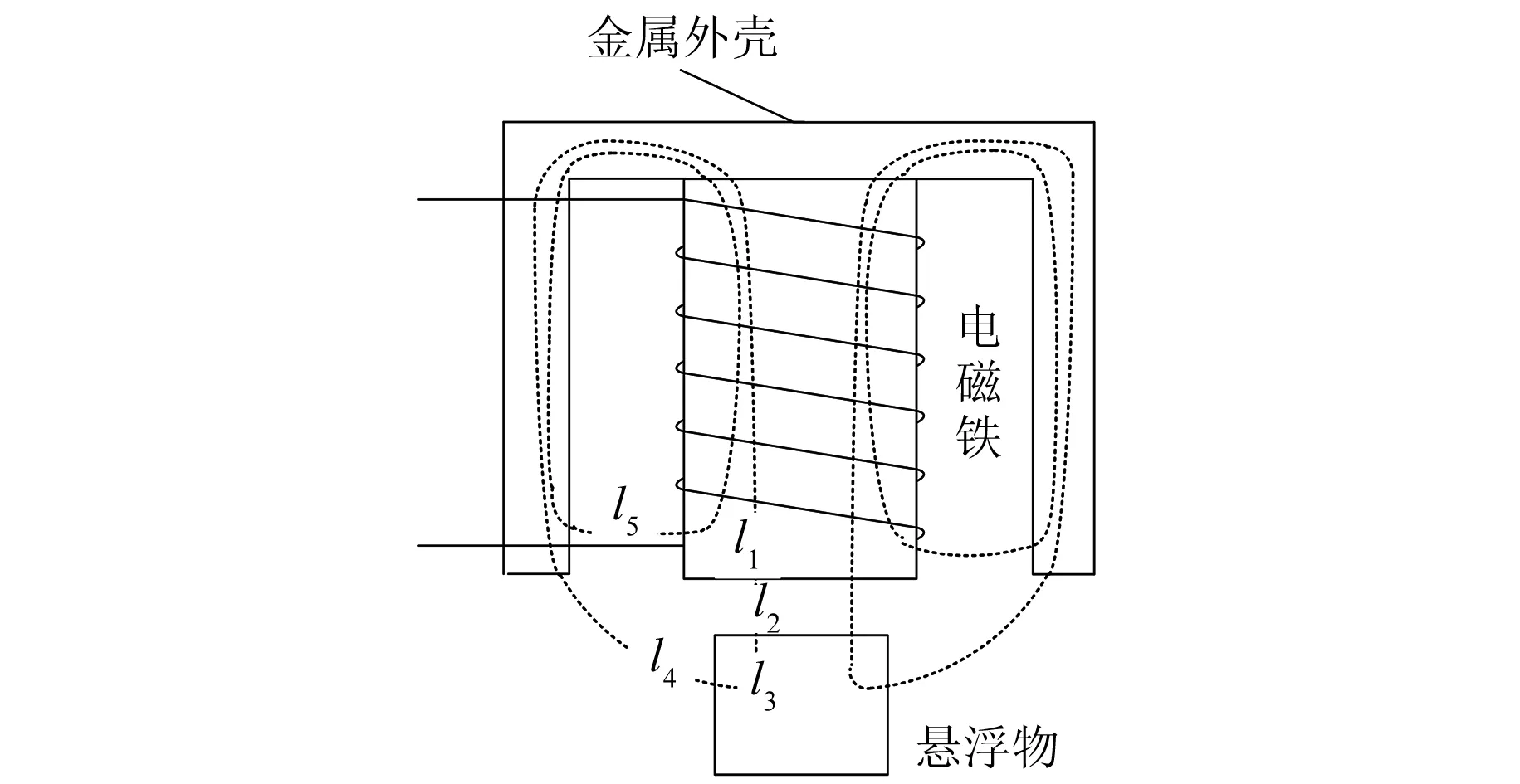
圖1 單自由度電磁吸力懸浮系統模型
當電磁鐵中通入電流時,根據安培環路定律[11]有
H1l1+H2l2+H3l3+H4l4+Ni′=Ni
(1)
式中:l1~l4分別為電磁鐵及外殼、氣隙、懸浮物、懸浮物到金屬外殼間的積分路徑的等效長度;H1~H4分別為電磁鐵及外殼、氣隙、懸浮物內部、懸浮物到金屬外殼間的磁場強度;N為線圈匝數;i′為l5路徑上漏磁對應的電流分量。
假設磁場為均勻磁場,則式(1)可以改寫為
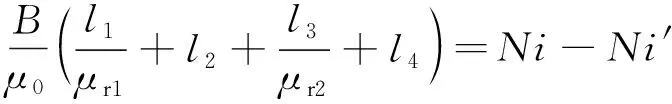
(2)
式中:μr1為電磁鐵的相對磁導率;μr2為懸浮物的相對磁導率,μr1=μr2=μr;B為磁感應強度;l2=δ,δ為懸浮氣隙值。顯然,積分路徑l4與氣隙存在比例關系。
式(2)可以表示為
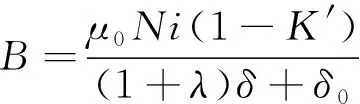
(3)

由于結構原因,會有一部分磁通只經過金屬外殼而不經過懸浮物。假設這部分漏磁Ni′不會隨氣隙變化而變化,而與流經電磁鐵中的電流正相關,則式(3)可寫為
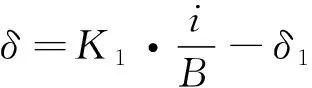
(4)

2 電磁場有限元仿真
為了驗證對式(4)假設的正確性,選取7 mm作為懸浮平衡點,對不同電流下的電磁模型進行有限元仿真。仿真參數如表1所示。仿真結果如表2所示。

表1 電磁鐵仿真參數
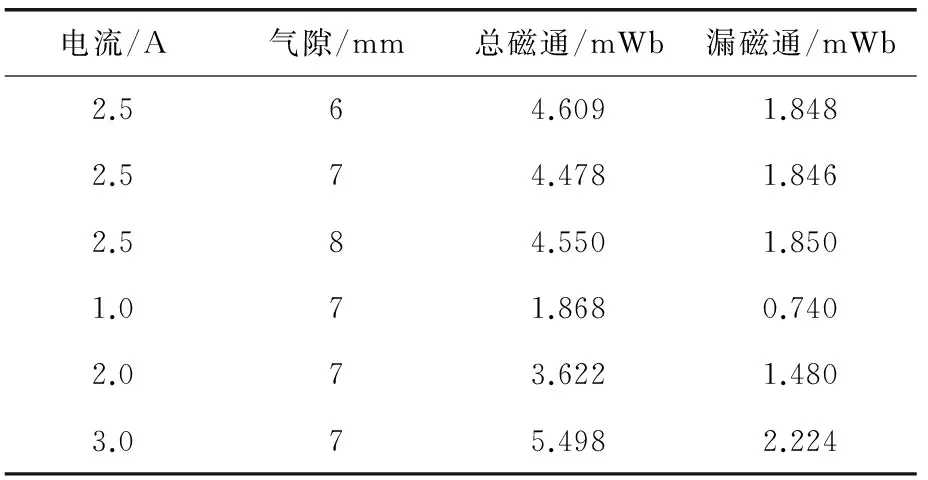
表2 仿真結果
由表2可知,漏磁大小與氣隙近似無關,與總安匝數近似成正比。
為了獲取更準確的磁場,設計了兩個磁場測量點,如圖2所示。位置1是懸浮物頂部幾何中心,位置2是電磁鐵底部幾何中心。仿真參數仍如表1所示。
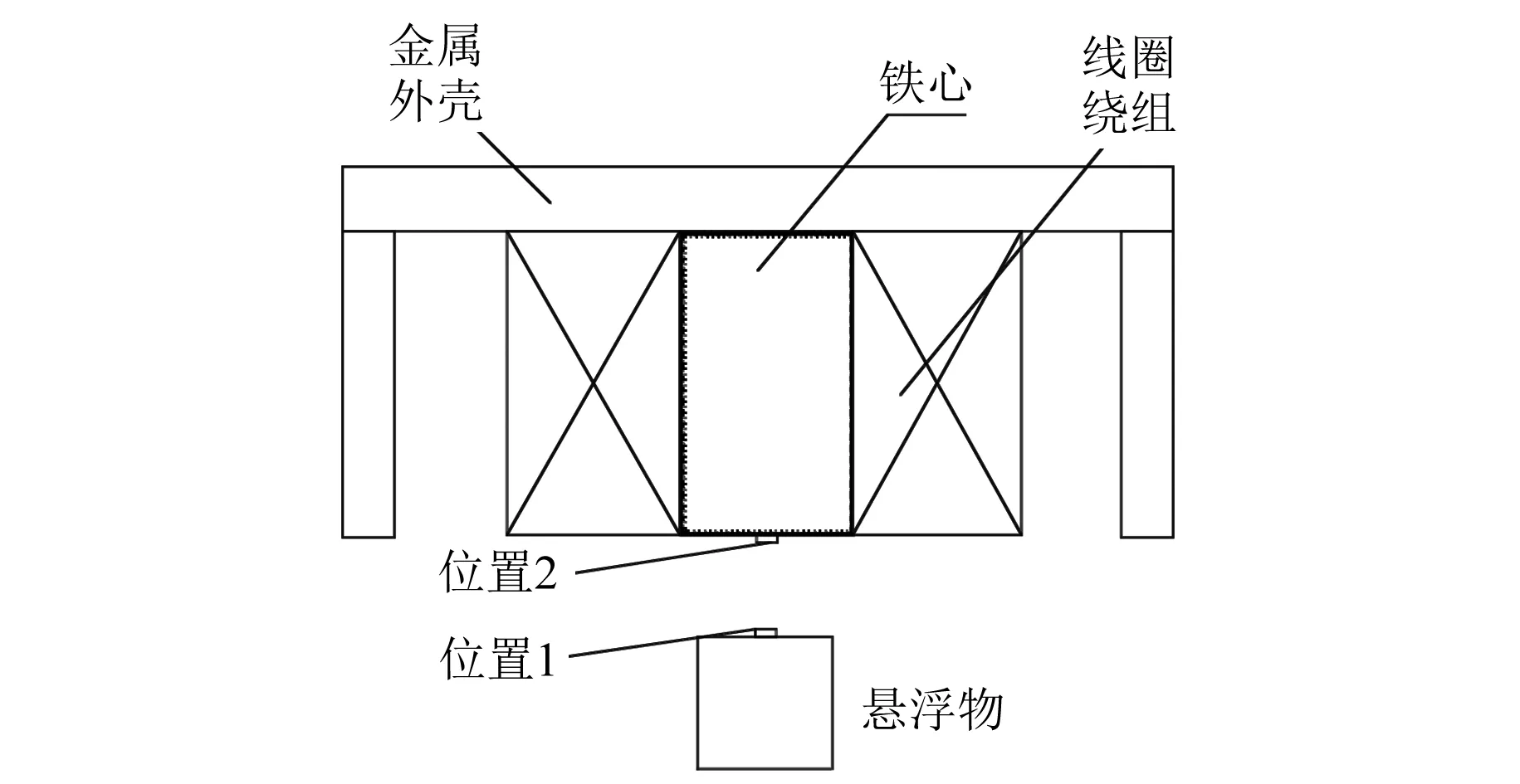
圖2 霍爾傳感器不同放置位置
氣隙為7 mm,電流為2.5 A時,磁密分布圖如圖3所示。
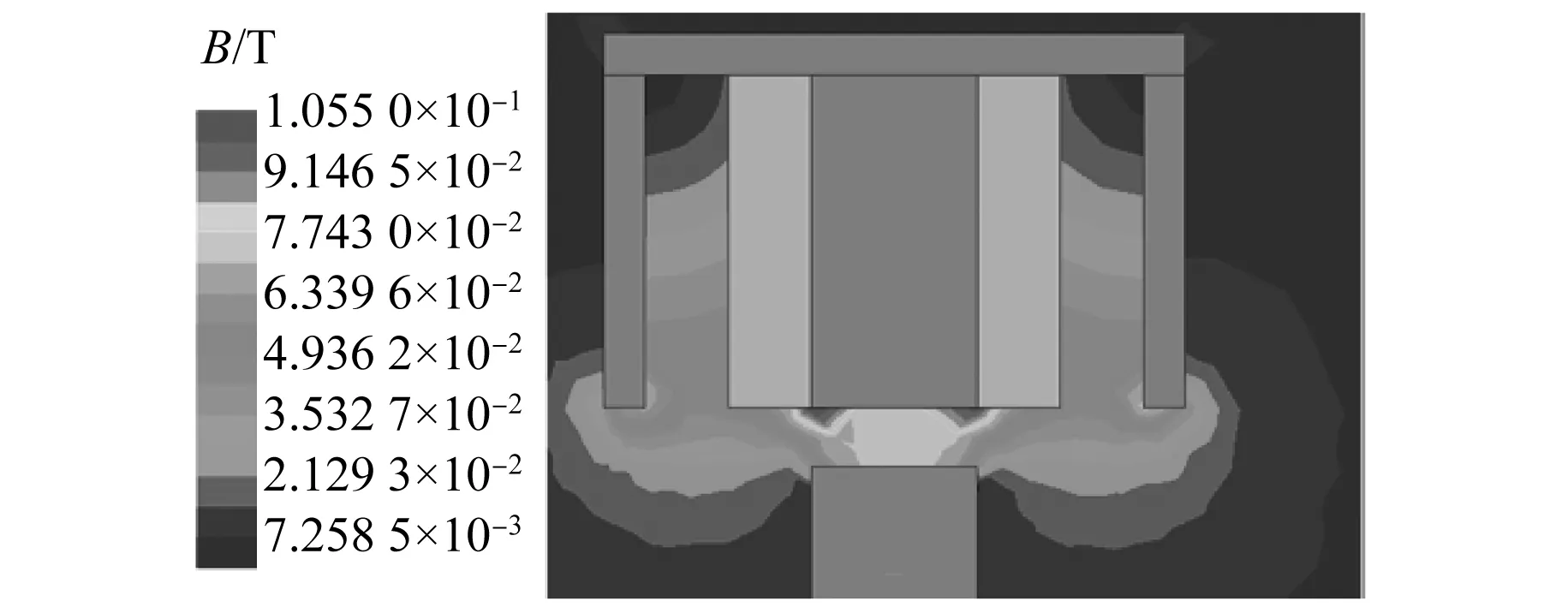
圖3 磁密分布圖
磁密分布圖顯示,氣隙為7 mm時,氣隙的磁感應強度僅為0.07 T左右,未達到懸浮物磁場強度的飽和值0.84 T,可以認為此時磁感應強度與磁場強度之間的關系為線性關系。
分別對位置1與位置2兩個位置的磁感應強度隨氣隙的變化情況進行仿真。結果如圖4所示。
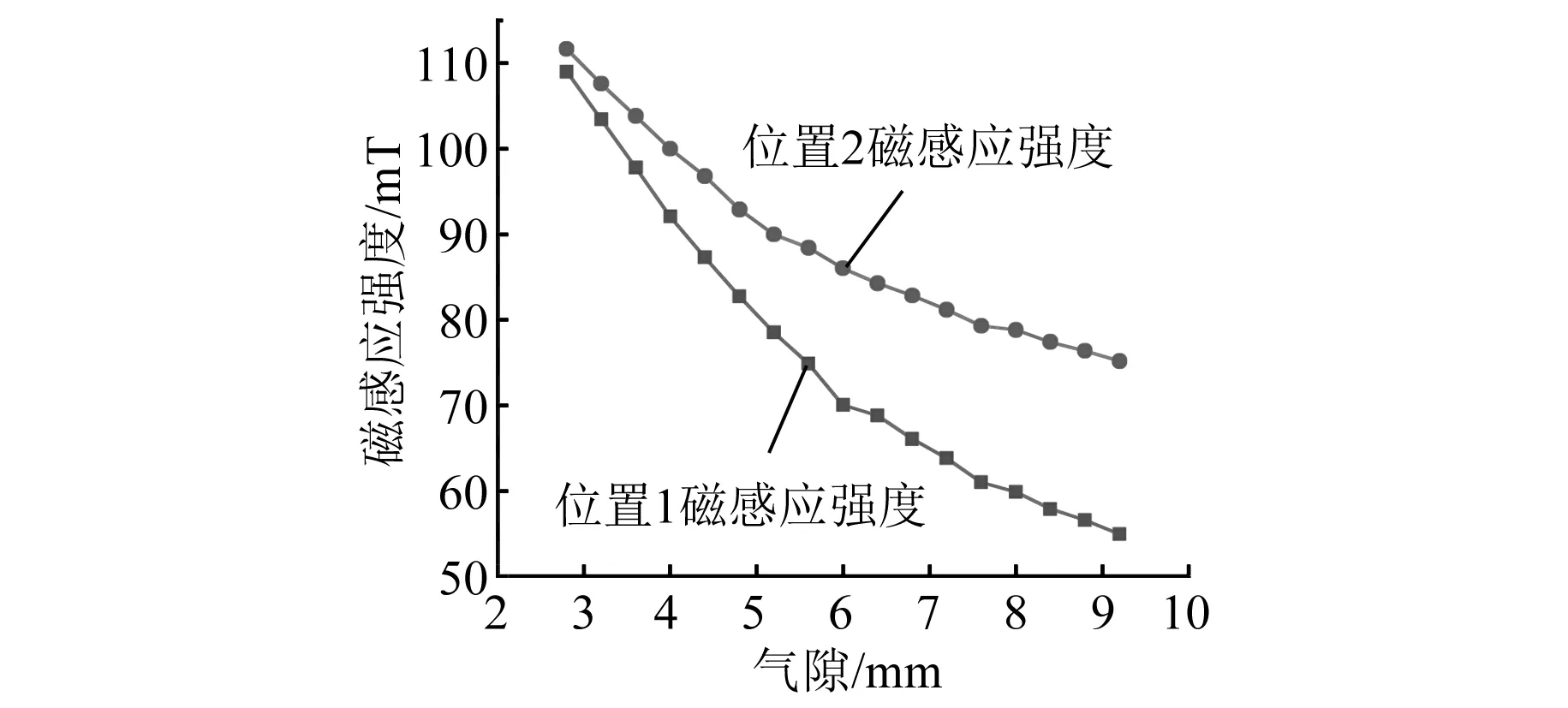
圖4 位置1、2磁感應強度值
大氣隙下漏磁不斷增多,導致位置1較位置2磁感應強度值變化更明顯。
3 磁場測量及傳感器安裝
由式(4)知,若K1已知,則可以借助通入電磁鐵中的電流和磁感應強度觀測氣隙,磁感應強度可以通過霍爾傳感器測量。與氣隙傳感器相比,霍爾傳感器安裝方便,成本低,更易于集成,可以通過磁場測量電路輸出一個電壓信號。磁場測量原理如圖5所示。
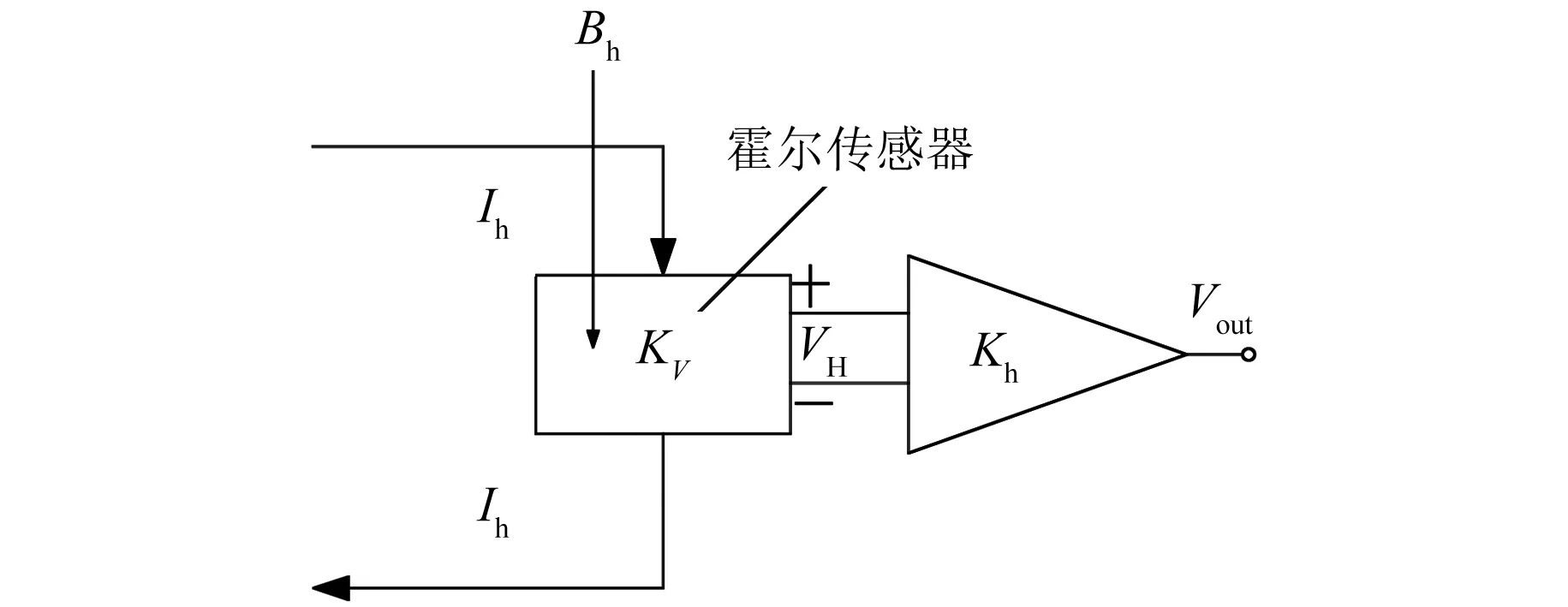
圖5 磁場測量原理
當通入霍爾傳感器中的電流Ih與通過霍爾傳感器的磁場感應強度Bh恒定時,霍爾傳感器兩端的電壓與溫度的關系為
VH=KT·T+a
(5)
式中:VH為霍爾傳感器兩端電壓;KT為溫度系數;KV為霍爾傳感器敏感系數;T為溫度;a為偏置。
磁場測量電路輸出的電壓與霍爾傳感器兩端電壓關系為
Vout=KhVH=KhKVIhBh+aKh
(6)
式中:Vout為磁場測量電路輸出的電壓值;Kh為磁場測量電路的放大系數。
在電磁鐵中通入2.5 A電流,測得在氣隙為7 mm時兩位置磁場測量電路輸出電壓變化情況如圖6所示。

圖6 相同電磁鐵電流下位置1與位置2的磁場測量電路輸出電壓
由圖6可知,當霍爾傳感器放在位置2時,隨著時間增加,磁場測量電路的輸出電壓先逐漸減小然后保持不變,這是由電磁鐵通入的電流導致電磁鐵溫度升高所致。當霍爾傳感器放在位置1時,輸出電壓基本保持不變。
綜上所述,位置1對磁感應強度的靈敏度高于位置2,且位置2易受到溫度影響,故將霍爾傳感器放置于位置1。

圖7 位置1的磁感應強度
將霍爾傳感器置于位置1,在線圈中通入2.5 A的電流。由表2知,可以近似認為在平衡點附近固定漏磁為總磁通的40%。計算式(4)中λ為0時的磁感應強度的理論值并對電磁懸浮模型進行有限元仿真,其磁場理論值、仿真值、實際值曲線如圖7所示。在平衡點附近,實際值與仿真值基本一致。部分計算與仿真結果如表3所示。
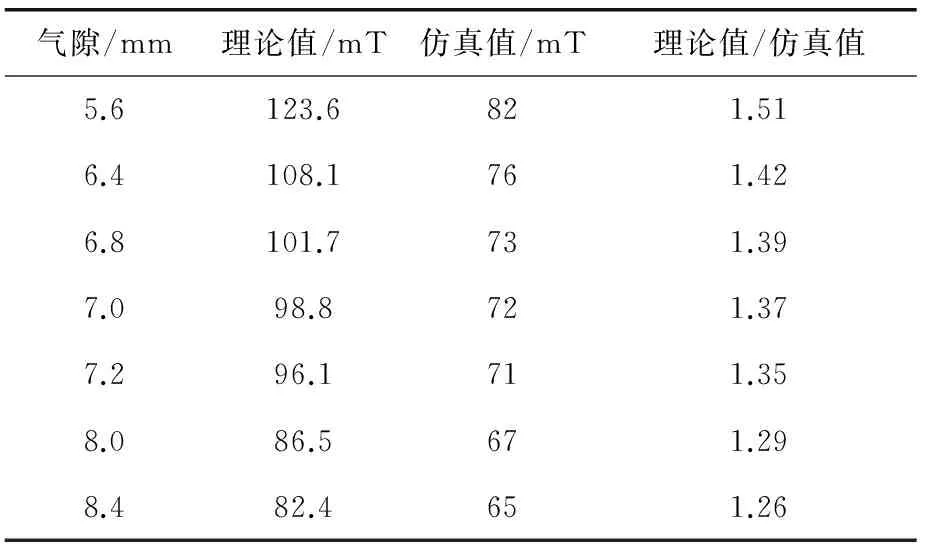
表3 計算與仿真結果
由于δ0?δ,可以忽略δ0對δ的影響,理論值與仿真值的比值即為1+λ在平衡點附近發生較小位移時的值。由表3可知,可以近似認為λ在平衡點附近為一常值。
4 氣隙觀測函數的設計
采集電路與懸浮電路結構設計如圖8所示。閉合開關2與開關3,斷開開關1,使得懸浮物在傳統模式下穩定懸浮。在平衡點附近上下拽動懸浮物,采集實時的氣隙、電流以及磁場信號,根據式(4)的形式進行擬合。閉合開關1,斷開開關2與開關3,將擬合函數運用到懸浮控制中,從而實現無氣隙傳感的懸浮。

圖8 采集電路與懸浮電路結構
4.1 觀測氣隙的擬合
加入霍爾傳感器和磁場測量電路,采集懸浮物在平衡點周圍的磁場測量電壓、線圈電流以及氣隙值。采用兩種方法對這些實測數據開展分析,進行觀測氣隙擬合。
方法一:非線性曲線局部線性化。將式(4)在平衡點附近展開,并忽略二階及其以上項,有:
δ=f(i,B)=Δδ+δ1=
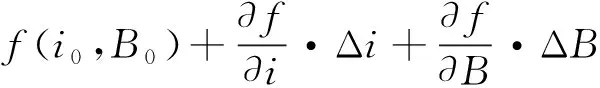
(7)
式中:i0為平衡點的電流值;B0為平衡點的磁感應強度值;δ1為設定的氣隙參考值;Δδ為實際氣隙與參考氣隙的差值。
將f(i0,B0)=δ1代入式(7)有:
Δδ=KI·Δi+KB·ΔB
(8)
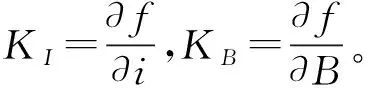
此方法可以很好地解決平衡點線性化的問題,但擬合函數中有兩個變量,增加了函數擬合的復雜性。此外,這種方法只在平衡點附近很小的范圍內適用,當有大擾動發生時,最終的控制效果會偏離預期。

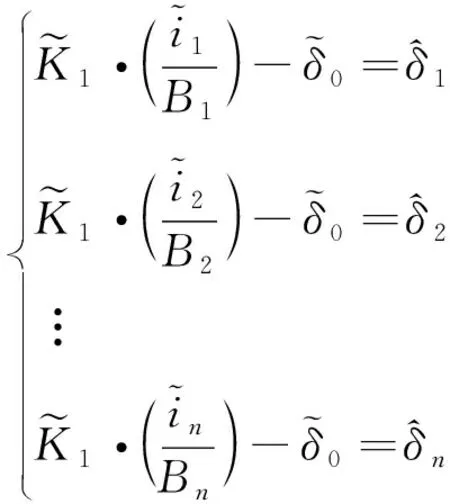
(9)

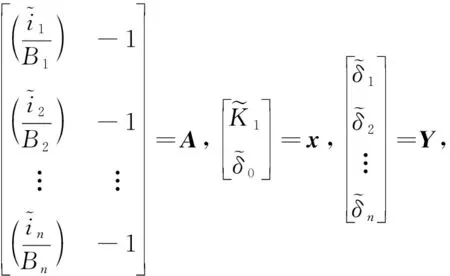

(10)
通過試驗測得的部分數據如表4所示。
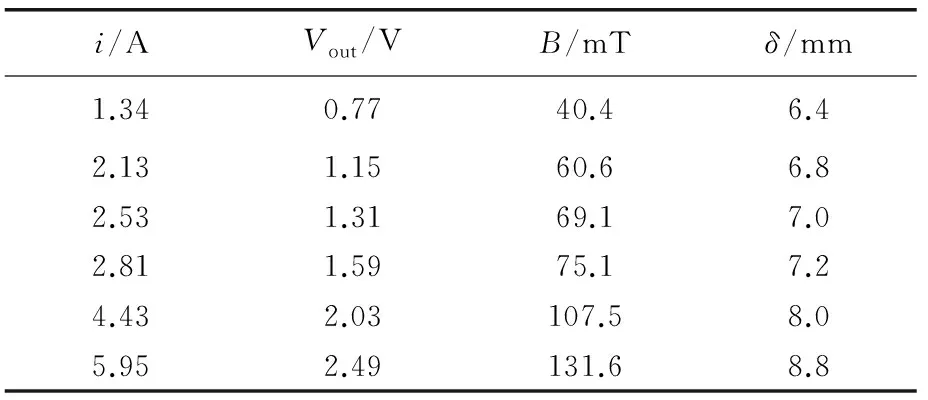
表4 實測數據
4.2 觀測氣隙試驗
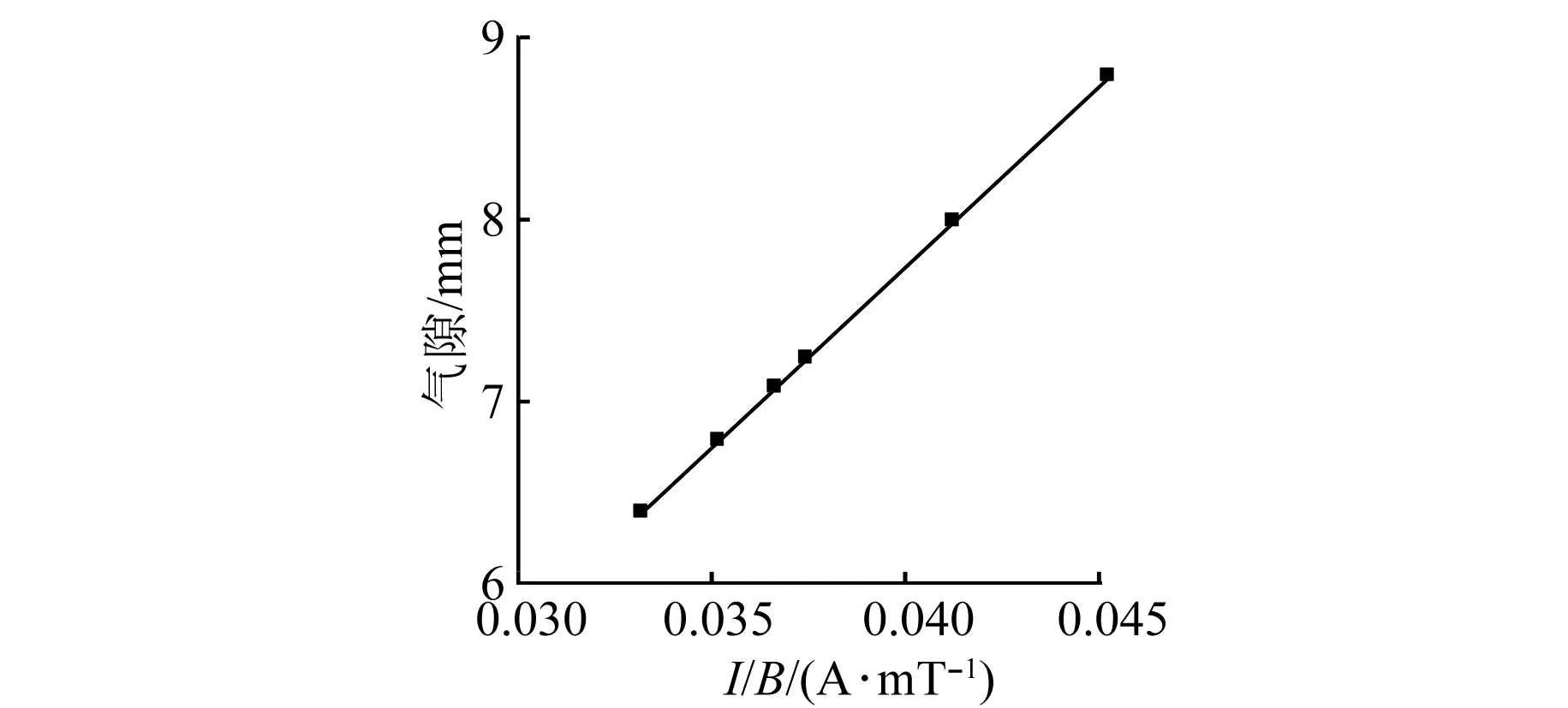
圖9 氣隙函數擬合曲線
為了確定氣隙觀測函數的可靠性,在平衡位置附近上下拽動懸浮物,繪制了實際氣隙曲線與觀測氣隙的動態波形,如圖10所示。

圖10 實際氣隙與觀測氣隙動態波形
由圖10知,觀測氣隙可以跟隨實際氣隙。
5 觀測氣隙的仿真與分析
5.1 觀測參數對閉環系統的影響
采用PD控制下懸浮系統的動力學方程組為

(11)
式中:m為懸浮物質量;g為重力加速度;F為所受磁場力;fd為外界干擾;kp、kd分別為控制系數。
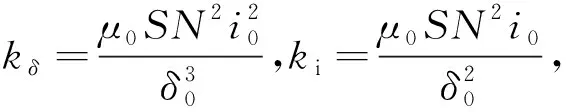

(12)
式中:k′d=kdki,k′p=kpki-kδ。
采用觀測氣隙作為反饋有
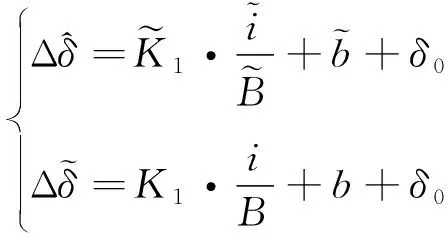
(13)
則:

(14)
將式(14)代入式(12)得:

(15)

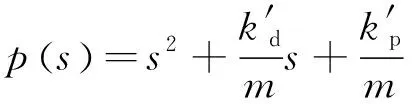
(16)
5.2 觀測氣隙在閉環系統中的控制仿真
為了驗證試驗的可行性,根據圖6在Simulink仿真條件下搭建了傳統控制方式實現懸浮物在氣隙為7 mm處的懸浮模型,并將擬合的氣隙觀測函數加入氣隙辨識模型中,如圖11所示。
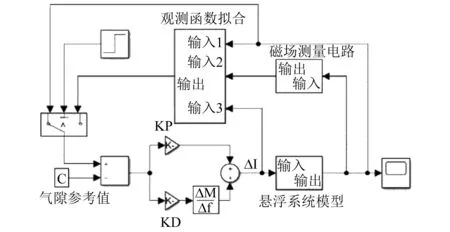
圖11 Simulink仿真模型
為了檢驗氣隙觀測函數的可靠性,在模型中加入方波擾動。兩種不同控制方式下的氣隙響應曲線如圖12所示。

圖12 兩種控制下的響應曲線
由圖12可知,基于霍爾傳感器的懸浮控制在擾動下的響應與傳統PD控制響應基本一致。
6 試 驗
現將得到的氣隙觀測函數應用到懸浮控制電路中。由于沒有使用氣隙傳感器,在放入懸浮物之前在電磁鐵中通入I=2.5 A的電流產生磁場,然后將懸浮物放到平衡點附近,待磁場檢測電路檢測到有輸出電壓時取消恒定電流。實際懸浮效果如圖13所示。

圖13 懸浮試驗平臺
繪制懸浮物的浮動波形如圖14所示。由圖14可知,通過氣隙觀測函數作為氣隙反饋的方法,可以實現懸浮物在氣隙為7 mm處的懸浮。
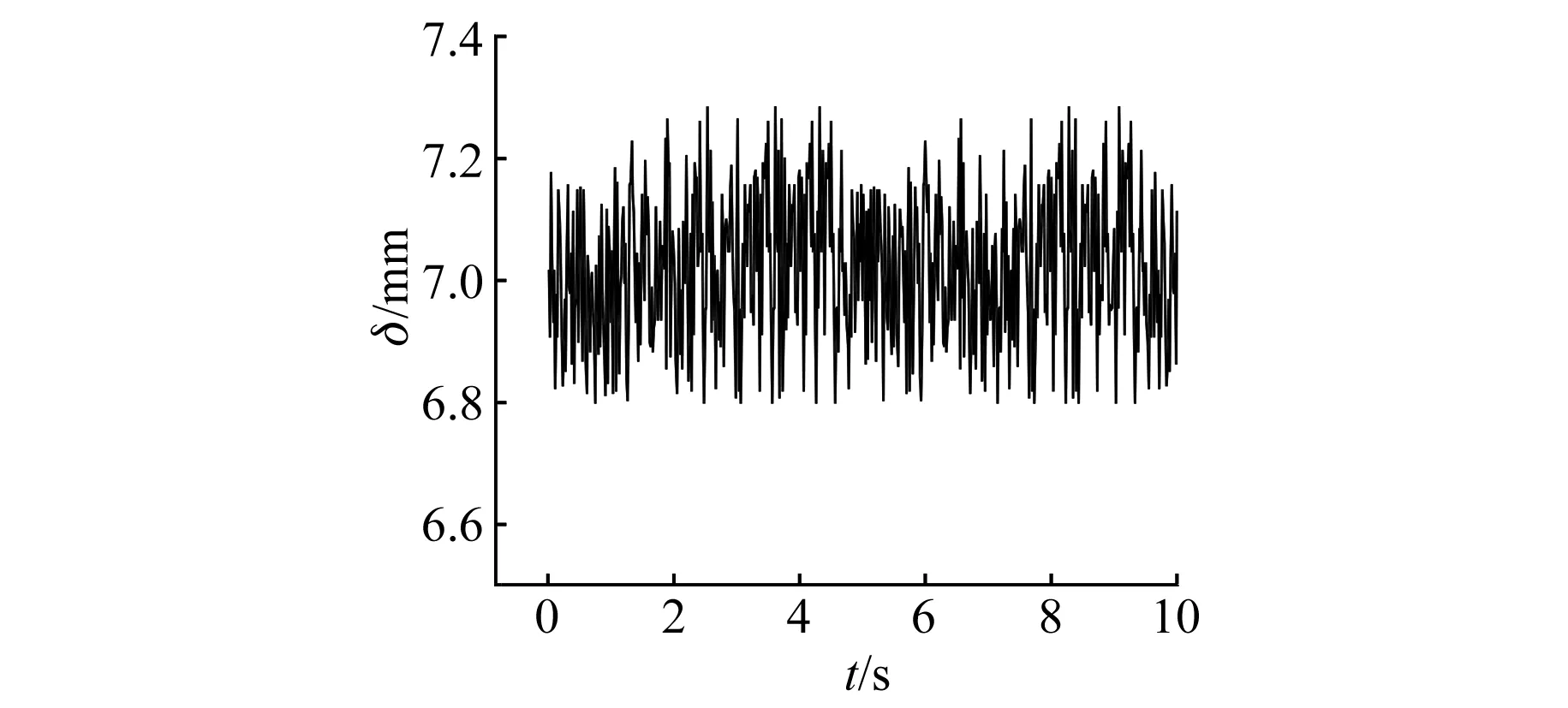
圖14 懸浮物浮動曲線
7 結 語
提出了一種基于氣隙辨識的無氣隙傳感器懸浮系統,推導了氣隙與電流和磁感應強度的數學模型,利用有限元仿真軟件對數學模型進行仿真。分析了利用擬合氣隙作為氣隙反饋的方法,并將擬合函數應用到懸浮控制系統中。試驗表明,懸浮物實現了在氣隙為7 mm處的懸浮。

