換元法在復合函數求導中的應用

覃桂茳 羅秀峰 黃麗清 趙春茹* 覃學文 （.梧州學院，廣西 梧州 54300；.長洲中學，廣西 梧州 54300 ）

引 言

在新課標理念的倡導下，對數學學科教學工作開展了一系列詳細的規定，圍繞數學課程設計、課程性質、課程內容與課程目標均有了確切的要求，可以說新的課程標準為教師提供了更清晰的教學思路與更精確的培養方向.高二數學（人教版）選學2-2 第一章“導數及其應用”的教學理念是“實踐——理論——實踐”，先通過瞬時速度、切線斜率的極限思想導入導數概念，再到導數的應用，讓學生在學習數學的過程中由傳統的知識理解型學習模式逐漸轉變為知識應用型實踐模式，推動學生創新能力的發展.

1 案例分析

導數及其應用內容在每年的全國高考數學卷中均有一道大題，分值是12 分，分數占整卷的8 %.學生作為初學者去學習這部分內容是非常困惑的，主要表現在沒有記全基本初等函數的求導公式，記錯乘法、除法導數運算公式，使用復合函數求導公式缺項或者多項等，即使在進行了多次的強化專項訓練后，學生還是沒有完全掌握導數計算的技巧.為了幫助學生掌握函數導數的求法，筆者結合教學實踐對一道例題進行多種方法的求解.

已知＝＝sincos求導函數

（一）＝（sincos）＝（sin）cos+sin（cos）＝cos-sin

注：首先利用兩個函數相乘的導數公式：［（）（）］＝（）（）+（）（），然后用到了兩個基本初等函數的導數公式：（sin）＝cos，（cos）＝-sin

2 利用換元法計算導數

設＝（），∈，而＝（），∈，當D∩Z≠?時，將＝（）代入＝（）中，得到＝（（）），稱函數（）和（）構成復合函數（（）），簡記＝°（），其中法則為內函數，法則為外函數，稱為中間變量.

解答完畢后，與學生互動交流，要讓學生得出“計算的結果一樣”的結論.由具體到抽象，培養學生思維能力，如由列舉的具體換元變量＝2，＝sin，＝tan到換元＝（），且不論（）是關于的何種表達式，復合函數求導公式y′＝y′·u′的結果是一樣的.那么，需要思考如何選取簡潔的、有利的、恰當的表達式（），使得計算復合函數導數的過程最為便捷.

3 選取元的原則

利用換元法是高中數學解題過程中的基本方法，同時也是學生在實際應用中的難點.在復合函數的分解過程中，選取恰當的元相當于選擇恰當的中間變量.對任意的中間變量＝（），總有y′＝y′·u′.在利用多種方法計算導數時，要教會學生識別哪些方法是簡潔的、具有優勢的，特別是當出現復合函數時，需要進行由外至內的分解，找準中間變量，并落實復合函數求導公式的應用.通過布置課堂練習“例2”，讓學生熟練掌握復合函數的分解要領與原則.

復合函數＝lnsin由哪些基本初等函數復合而成

構造5 種分解法，具體如下：

①＝lnsin＝ln，其中＝sin＝（）.

②＝lnsin＝sin，其中＝arcsin（lnsin）＝（）.

③＝lnsin＝tan，其中＝arctan（lnsin）＝（）.

④＝lnsin＝cos，其中＝arccos（lnsin）＝（）.

讓學生明白這5 種換元法從本質上看都是正確的，然而，部分方案與由繁化簡才引入換元法的目的相矛盾.方案①中，變量＝（）＝sin（）是關于的1 種法則（正弦法則），在除①外的其他方案中，變量＝（）都是關于的3 種法則，比函數＝lnsin本身的2 種法則（對數法則和正弦法則）多.函數＝lnsin是關于的2 種法則，分別是先取正弦法則，再取對數法則.研究復雜的＝lnsin轉移到研究＝（），不難發現，只有方案①具有優勢（法則次數少）.可以說，復合函數分解的原則是中間變量＝（）很容易得出，且相比函數（）的運算法則少1 次（種）法則.

函數＝lnsin由初等函數＝ln，＝sin復合而成.

注：對復合函數的分解，選取中間變量的原則就是中間變量的表達式關于變量的初等法則次數要少于分解的函數.

4 鏈式法則求導推廣

若復合函數＝（）是可導的，且函數＝（）由＝（），＝（），＝（）初等函數復合而成，其中，為中間變量，則有鏈式法則求導公式

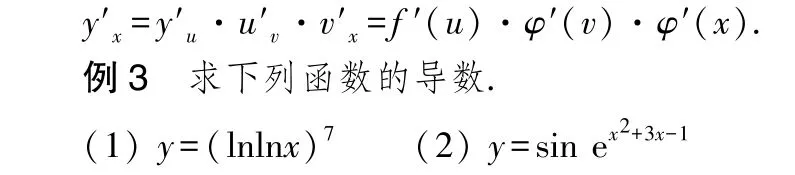
（1）函數＝（lnln）由＝，＝ln，＝ln復合而成.由鏈式法則可知，

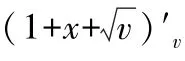
5 舉例應用

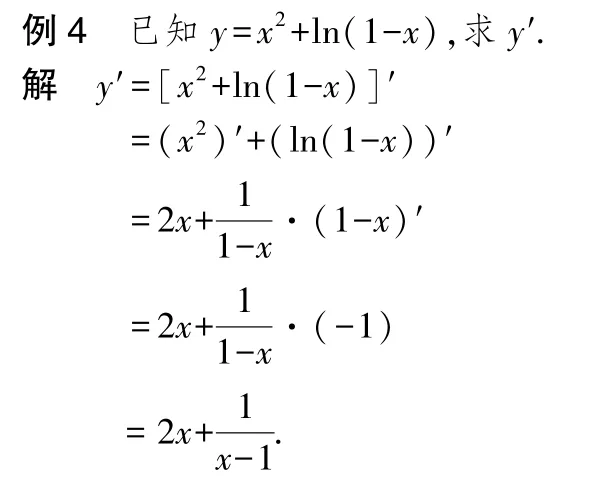
注：復合函數＝ln（1-）由初等函數＝ln，＝1-復合而成.

6 實施有效教學監督

教學質量監控是指監控組織成員（教務處督導、同行教師、班級學生）通過對教學質量的持續監督，在分析整理教學工作質量、教學成果質量等方面信息的基礎上發現可能存在的問題，對教學行為及時調控，以穩定和提高教學質量.

以復合函數求導的教學設計為例，利用兩次統計檢驗學生對該教學內容的掌握程度.例1 講解結束后，給出評分細則，讓學生進行自我評分，然后教師統計學生得分情況，詳情見表1.從統計表中，可知班級共有47 位學生，有8 位學生獲得6 分，占比17.02%，12 位學生獲得4 分，占比25.53%，該題滿分是6 分，平均分是3.34 分，有57.447%的學生超過平均分，與教學計劃中預期的平均分4 分存在一定的差距，這里就不再分析原因了.

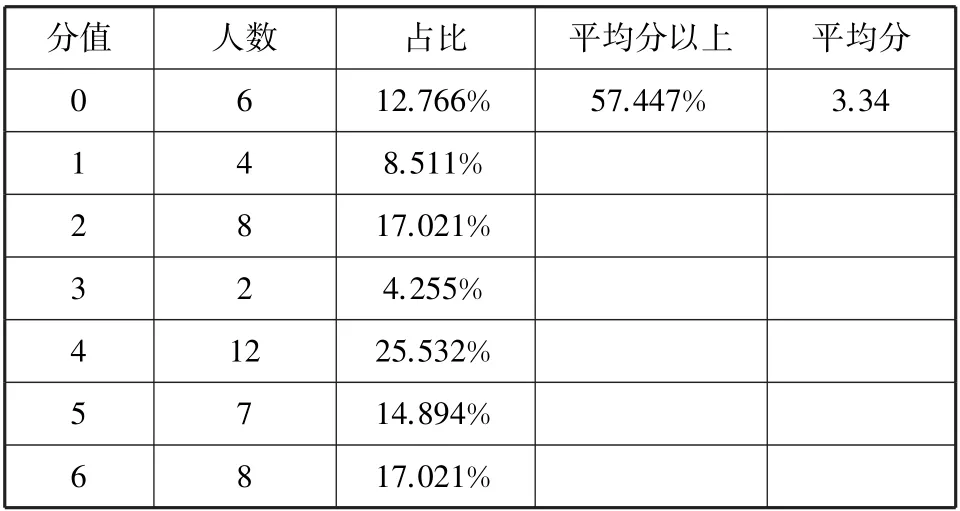
表1 班級主觀題自測評分統計表

在講解例2 過程中，讓學生選擇5 種換元法中正確的數量是多少，共設4 個選項，分別是0 項、1 項、3 項和5 項，學生答題的結果詳見表2.從表中看出，47 人的班級中有6 人選擇正確，有41 人選錯答案，選擇正確的占班級人數的12.766%，平均分是0.638 分，有12.766%的人超過平均分.顯然，學生對換元法的掌握不夠牢固，需要加強換元法的應用，培養學生的創新能力.

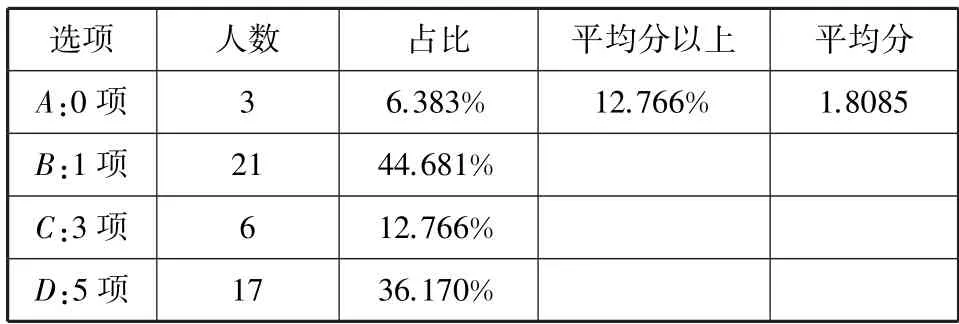
表2 班級選擇題評分統計表

（選擇題設置的分數是5 分）

教學過程中，我們可以在例1 的解法（四）、例2 復合函數的分解方面引導學生獨立思考，模仿解題思路，培養學生的創新意識，激發學生的創新性能力，把知識轉化為解決問題的能力.因此，在教學中，學生對教學內容的理解情況，將會是老師進行下一步教學至關重要的信息，所以在教學中教師必須要及時利用準確的、多方位的、多角度的信息反饋，引導學生主動探究，進行教學方法、教學手段的改革.

7 小 結

本文通過課堂習題的訓練，找出復合函數分解的準則，引入換元法輔助學生理解一元函數的微分不變性，并掌握復合函數的求導公式.教師應當結合布置的課后作業、習題訓練，開展循序漸進的教學，鞏固學生的基礎知識，多留一些時間給學生思考，找規律，自我消化，讓學生能夠掌握數學思想方法，切不可為了完成教學進度而早早結束本節教學內容.教師應當盡可能多地對學生的作業進行批改以及檢查，利用反饋信息，有針對性地調整教學計劃.在數學學習、教學過程中，要重視培養學生發現問題、解決問題的能力，讓學生用自己的思維，勇于解決數學問題，實現數學的應用.