對稱性在積分計算中的應用

姚曉閨 陳俊霞 丁小婷 （陸軍炮兵防空兵學院基礎部數學教研室，安徽 合肥 230031）

一、定積分的對稱性及其應用

若f（x）在［-a，a］上可積，則

二、重積分的對稱性及其應用

1.二重積分的對稱性原理

二重積分具有以下對稱性：

設二元函數f（x，y）在平面區域D 內連續，且D關于x 軸對稱，則

當D 關于y 軸對稱時，也有類似結論.

設二元函數f（x，y）在平面區域D 內連續，且D關于x 軸和y 軸都對稱，則

設二元函數f（x，y）在平面區域D 內連續，D＝D∪D，且D，D關于原點對稱，則

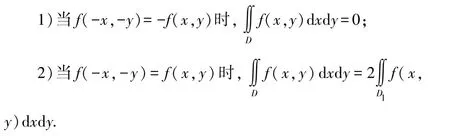
設二元函數f（x，y）在平面區域D 內連續，D ＝D∪D，且D，D關于直線y＝x 對稱，則

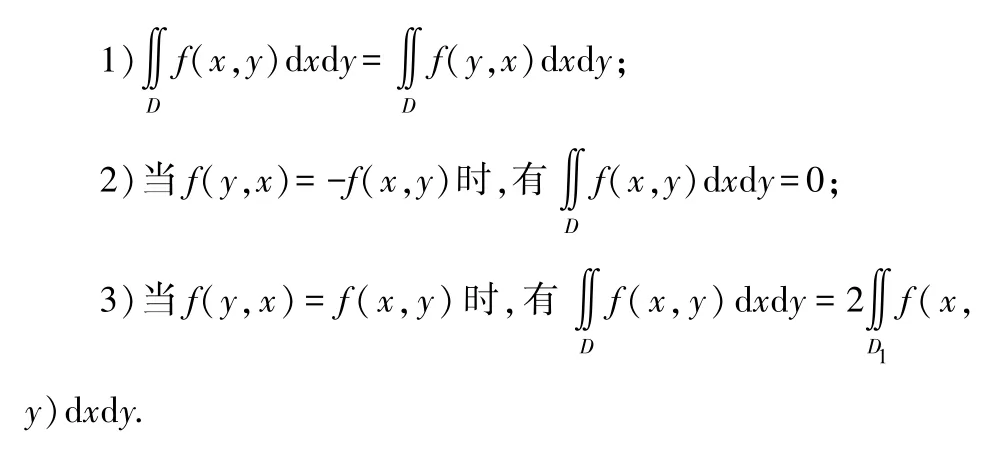
當D，D關于直線y＝-x 對稱時，也有類似結論.

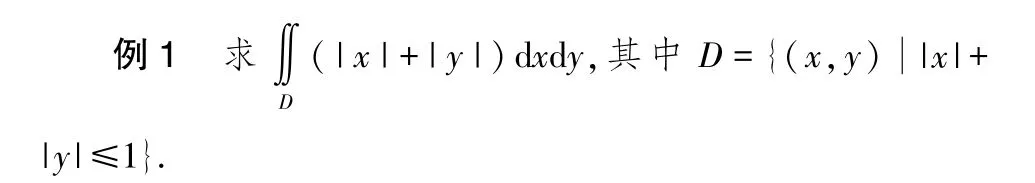
易知題中被積函數｜x｜+｜y ｜為x，y 的偶函數，且D區域具有對稱性.

2.三重積分的對稱性原理

設f（x，y，z）在區域Ω 上可積，Ω 關于xOy 面對稱，Ω是Ω 在xOy 面上方部分，則有

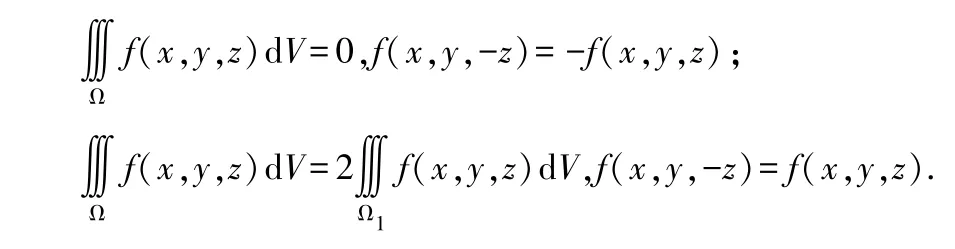
當Ω 關于其他坐標面對稱時，也有類似結論.

設f（x，y，z）在區域Ω 上可積，Ω 關于原點對稱，Ω是Ω 位于過原點O 的平面一側的部分.則有

注意到Ω 關于yOz 面對稱，而Ω關于三個坐標面都是對稱的，所以

三、對弧長的曲線積分的對稱性及其應用

設L 是平面上分段光滑的曲線，且P（x，y）在L上連續.

1）若L 關于x 軸對稱，則

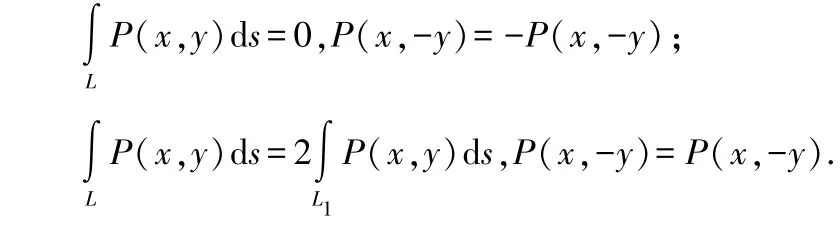
其中L是L 在上半平面的部分.

當L 關于y 軸對稱時，也有類似結論.

2）若L 關于原點對稱，則

四、對面積的曲面積分的對稱性及其應用

設有界光滑或分片光滑曲面∑關于xOy 平面對稱，f（x，y，z）為曲面∑上的連續函數，則

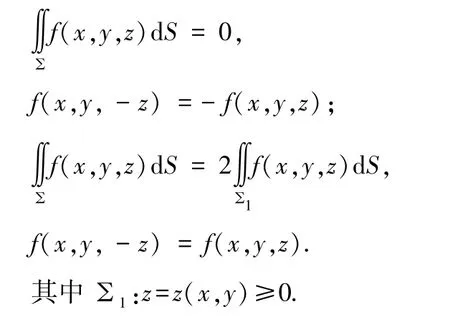
當∑關于yOz 面、zOx 面對稱時，也有類似結論.

五、積分區域關于積分變量具有輪換對稱性情況下的積分

設Ω∈R，如果（x，y，z）∈Ω 時，都有（z，x，y），（y，z，x）∈Ω，，則稱區域Ω 關于變量x，y，z 具有輪換對稱性.

定理1設積分區域Ω 關于變量x，y，z 具有輪換對稱性，則有

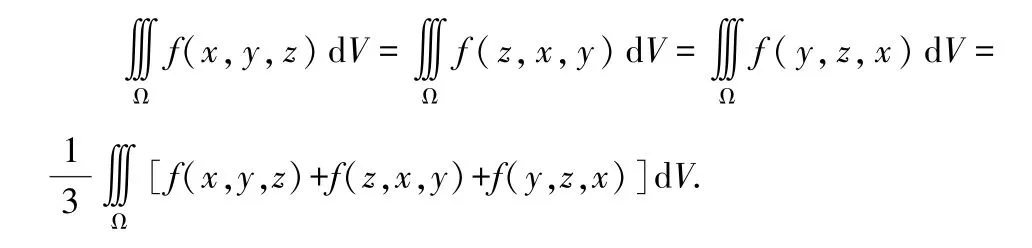
設積分區域Ω 關于變量x，y，z 具有輪換對稱性，則有

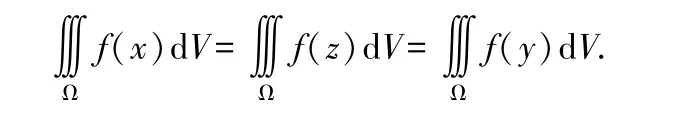
設積分區域D 關于變量x，y 具有輪換對稱性，則有

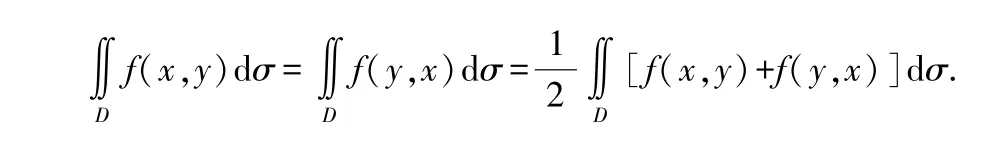
對于第一類曲線積分和曲面積分，同理可得到如下定理：

設曲線Γ 關于變量x，y，z 具有輪換對稱性，則有

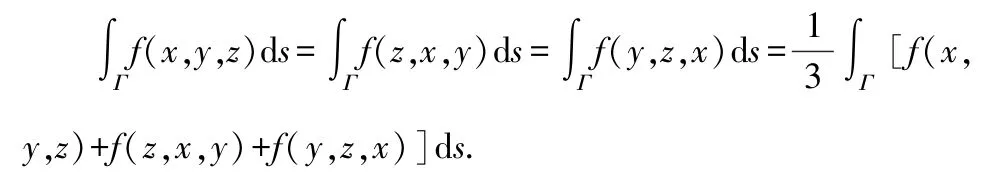
設曲面∑關于變量x，y，z 具有輪換對稱性，則有

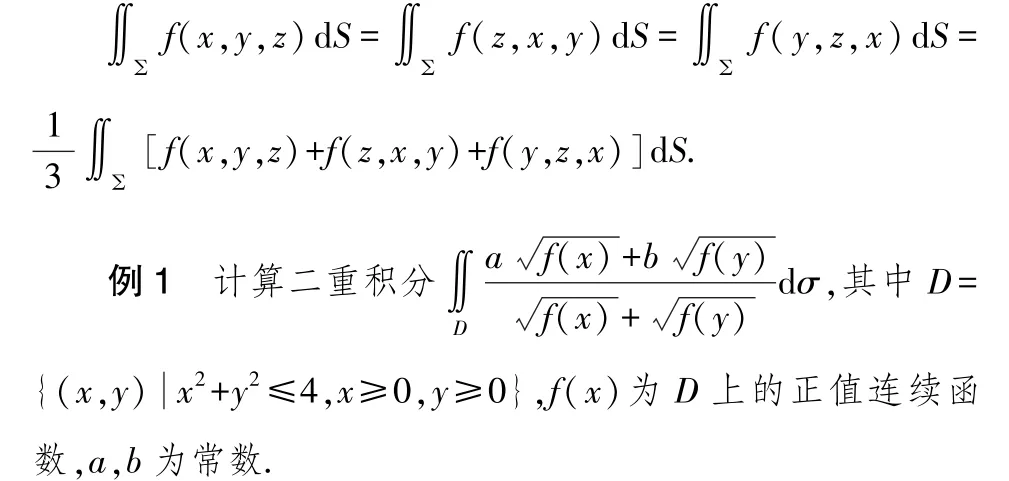
易知積分區域D 關于變量x，y 具有輪換對稱性，由定理2，得

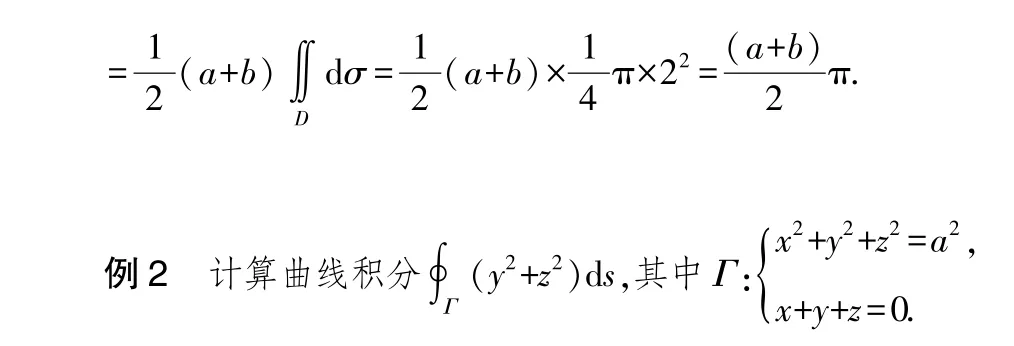
因為積分區域Γ 關于變量x，y，z 具有輪換對稱性，由定理3，得

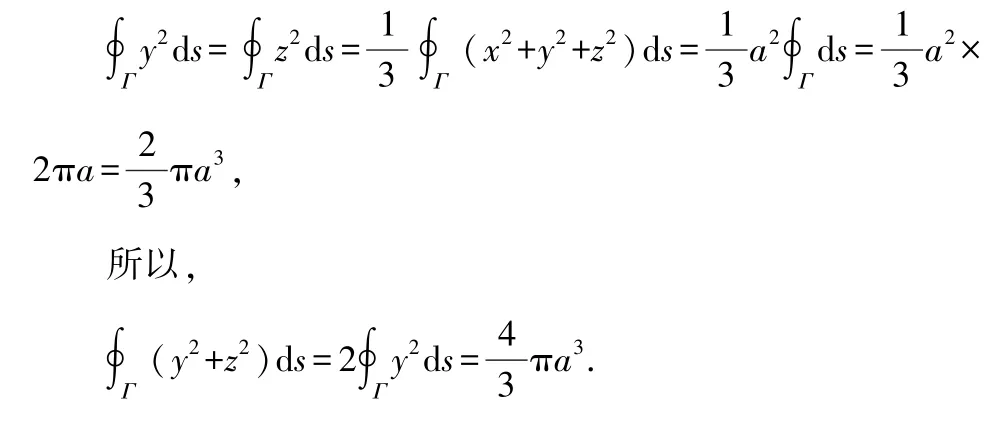
六、結束語

本文通過實際例題有力地說明了對稱性方法對計算效率的提高和優化是切實可行的.通過各類積分綜合題的計算回顧了對稱性的相關知識點，較好地說明了對稱性在積分計算中的應用.與其他解題方法相比較，對稱性由于其顯著的優化作用和簡單易用，在積分領域一騎絕塵，得到了廣泛的應用，使讀者在領略數學獨特魅力的同時，還激發人們無盡的想象力，使對稱性的應用充滿無限的可能.