FrFT-OFDM系統中聯合ICI自消除方案

王震鐸, 朱云飛, 寧曉燕,*, 刁 鳴

(1. 哈爾濱工程大學信息與通信工程學院, 黑龍江 哈爾濱 150001; 2. 先進船舶通信與信息技術工業和信息化部重點實驗室, 黑龍江 哈爾濱 150001)

0 引 言

正交頻分復用(orthogonal frequency division multiplexing,OFDM)技術具有抗干擾能力強、頻譜利用率高等特點,在當今無線通信系統中占有重要地位。但是,OFDM系統的傳輸可靠性依賴于其子載波間的嚴格正交,然而在實際傳輸環境中載波頻率偏移與雙選衰落等因素均會破壞子載波間的正交關系,因此引入子載波間干擾(inter-carrier interference,ICI)從而降低OFDM系統通信性能。為了提升OFDM系統的抗干擾能力,文獻[5]提出了用離散分數階傅里葉變換(discrete fractional Fourier transform,DFrFT)代替OFDM系統中的離散傅里葉變換(discrete Fourier transform,DFT),使用一組正交啁啾(Chirp)信號基代替OFDM系統中的指數信號基,系統轉化為分數階傅里葉變換的正交頻分復用系統(fractional Fourier transform orthogonal frequency division multiplexing,FrFT-OFDM)。FrFT-OFDM系統中的每個子載波均為Chirp信號,相較于指數信號,Chirp信號存在調頻率可變的結構優勢,在不同的信道環境中,能通過調節調頻率以適應信道變化,選擇最優旋轉角度以抑制ICI,提升系統性能。文獻[15]對FrFT-OFDM系統在時頻雙選衰落信道下的ICI進行了詳細推導,為ICI消除方案的設計提供理論基礎。

雖然FrFT-OFDM對復雜信道環境的適應性能更強,但是若引入的ICI較強,該系統對通信性能的改善十分有限。為了進一步抑制ICI,需引入自消除編碼技術。自消除編碼技術作為一種ICI抑制方法，因其復雜度較低且性能較好的特點而受到廣泛研究。經典OFDM系統的自消除方法主要基于相鄰數據或對稱數據產生的ICI強度相近的理論,通過一定的編碼方式將同一符號分配在相鄰或對稱的子載波上,在接收端解碼后進行判決,該方法在僅存在載波頻率偏移的信道環境中性能較好,而在雙選信道環境下對ICI的抑制效果有限,且該類方法頻譜利用率較低。文獻[18]中對傳統自消除編碼進行了擴展并提出頻域編碼多項式(后文簡稱ZH方案),使得自消除編碼方式的靈活性顯著提升,且可以達到一定程度的對ICI的抑制效果,但是其最高的編碼效率僅能達到1/2。文獻[19]在此基礎上提出了ICI編碼矩陣設計方案,進一步提升了編碼的靈活性,但是該方案需要豐富的先驗知識進行矩陣參數設計,對信道估計的性能有較高的要求且提升了系統的復雜度。

現有文獻中少有對FrFT-OFDM系統中ICI自消除方案的研究,且OFDM系統的自消除方案直接運用于FrFT-OFDM系統時對系統性能的提升并不理想。針對上述問題,本文在文獻[19]的基礎上提出了一種適用于FrFT-OFDM系統的自消除編碼矩陣。而后,為了充分利用FrFT-OFDM系統的結構優勢,本文計算了自消除FrFT-OFDM系統在復雜信道環境下的最優旋轉角度的篩選區間并提出了相應的搜索方案。

1 ICI統計與分析

FrFT-OFDM系統框圖如圖1所示,假設一個具有個子載波的FrFT-OFDM系統,經過調制的發送符號(=0,1,…,-2,-1)經過逆DFrFT(inverse DFrFT, IDFrFT)后轉換為長度為的時域信號():

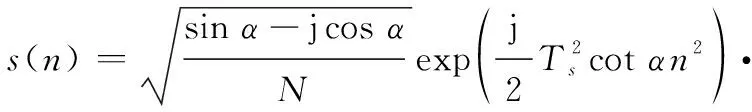
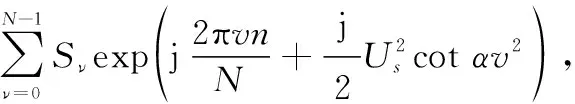
=0,1,…,-1

(1)

式中:為IDFrFT的旋轉角度;為時域采樣間隔;為階分數域采樣間隔。

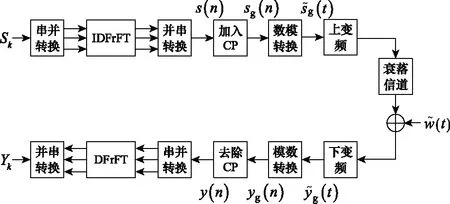
圖1 FrFT-OFDM系統框圖Fig.1 Block diagram for the FrFT-OFDM system

FrFT-OFDM系統加入循環前綴(cyclic prefix, CP)的方法,如圖2所示。

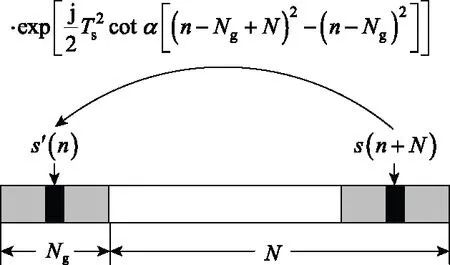
圖2 加入Chirp CPFig.2 Adding Chirp CP

將已調信號末端一定長度的信號運算后插入已調符號前端:

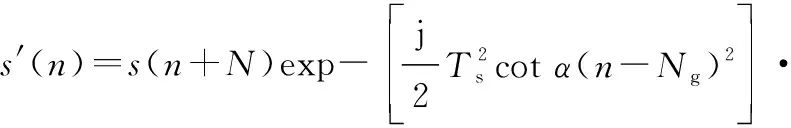
(2)

式中:為CP長度。添加CP后的信號()可表示為

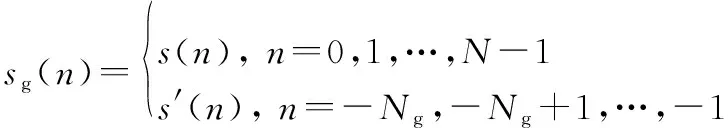
(3)

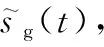
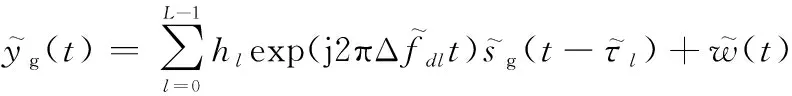
(4)

信號進行模數轉化并去除CP,在=時刻,得到時域接收序列為

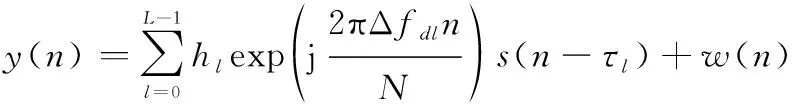
(5)

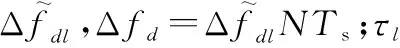
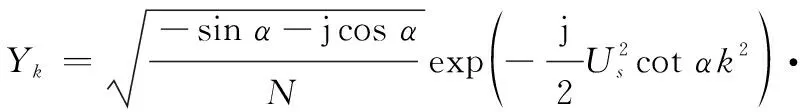
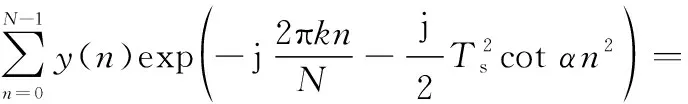
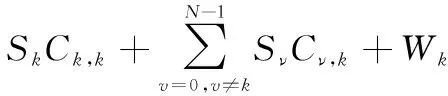
(6)

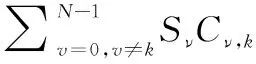
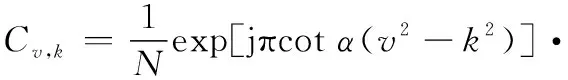
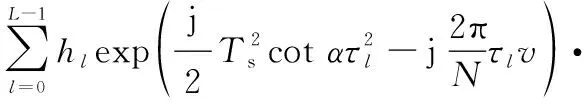
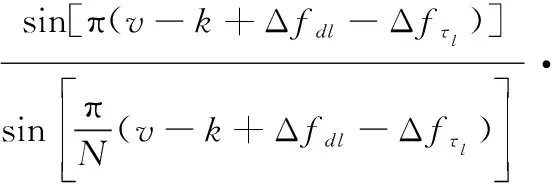
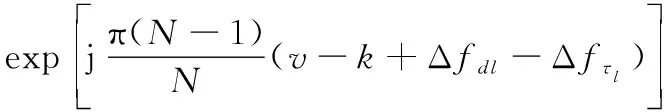
(7)

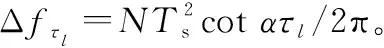
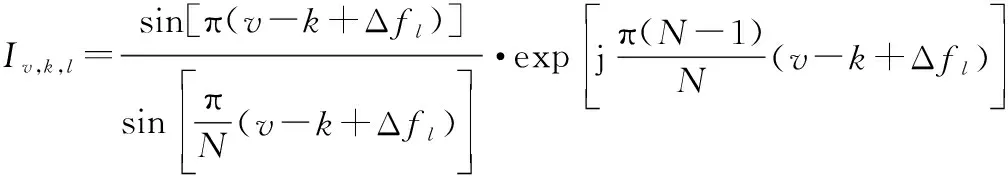
(8)

從式(8)中不難看出,Δ為第徑上產生ICI的主要原因,且Δ越大,干擾越強。若Δ=0在所有徑上均成立,則每徑的ICI系數均在=處取得最大值1,此時|,|在二維平面(,)上的分布如圖4所示。在該條件下僅存在沿對角線分布的期望信號的頻率選擇性衰落而不存在從對角線向兩側擴展的ICI。若Δ=0僅在部分徑上成立或者不成立,則在每條徑上期望信號的能量隨著Δ的增大而逐漸縮小,ICI逐步增強,該假設下的ICI系數的二維分布如圖5所示,|,|以對角線為中心向兩側逐漸展寬,且對角線上的期望信號能量下降,系統受到頻率選擇性衰落和ICI的雙重干擾。

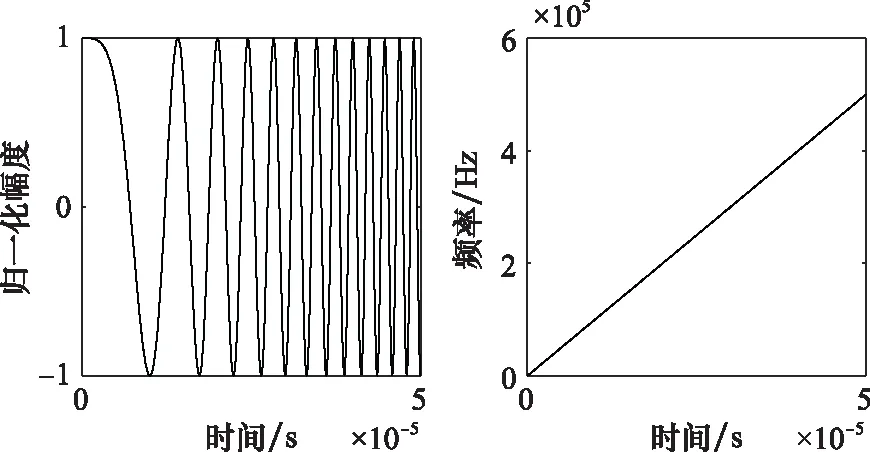
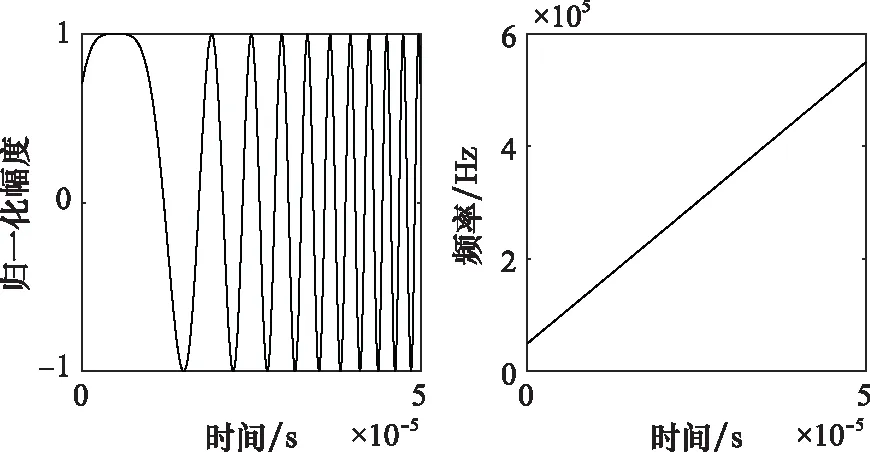
圖3 延時前后Chirp信號幅值與頻率比較Fig.3 Comparison between amplitude and frequency for the Chirp signal before and after time delaying

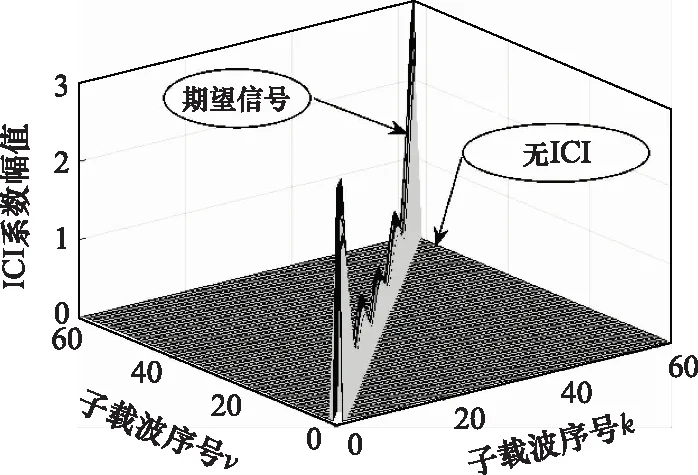
圖4 頻率選擇性衰落作用下的ICI系數二維分布Fig.4 Two-dimensional distribution of ICI coefficients under frequency selective fading

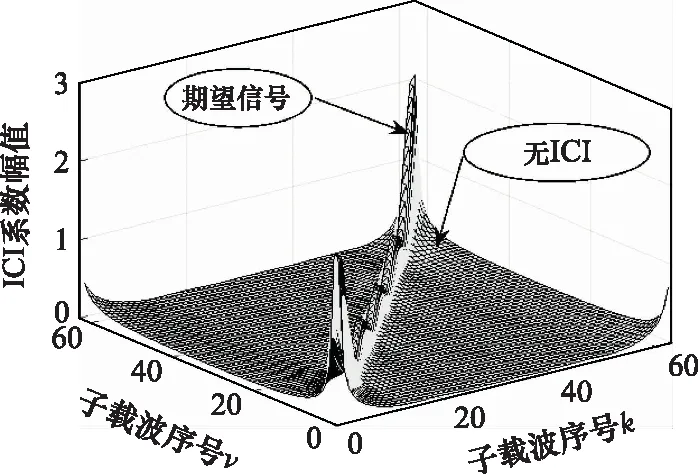
圖5 雙選衰落作用下的ICI系數二維分布Fig.5 Two-dimensional distribution of ICI coefficients under double selective fading

為了量化子載波所受ICI的強度,通常采用載波干擾比(carrier to interference ratio, CIR)作為度量標準,第個子載波的CIR表達式為

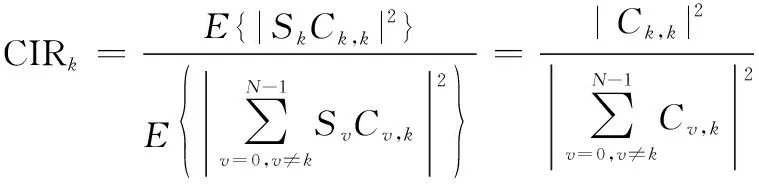
(9)

2 ICI自消除方法

2.1 ICI自消除編碼

針對傳統ICI自消除方法直接應用在FrFT-OFDM系統中所存在的問題,本文提出適用于FrFT-OFDM系統的ICI自消除編碼方法,假設發送端經調制后的擬發送符號為=[,,…，-1],經過自消除編碼后的符號為=[,,…,-1],則二者的關系可表示為

=

(10)

式中:為×階ICI自消除編碼矩陣,編碼效率為。從圖4與圖5中ICI系數的二維分布可以看出,ICI系數的鄰項幅值變化較小,因此在本文自消除編碼矩陣的參數設計過程中,只將符號的編碼值分配在相鄰子載波上,并假設相鄰項的ICI系數幅值近似相同,編碼矩陣每一行上取負的元素的幅值之和與取正的元素幅值相等。另一方面，為了使系統在接收端不需要進行解碼操作,降低系統復雜度,對于傳輸有用信號的子載波上的符號不進行編碼處理,即在接收端只要進行一次抽取操作便可獲取有效信號。基于上述編碼矩陣設計方案,以編碼效率12為例,可構建自消除編碼矩陣如下:

(11)

經過自編碼矩陣編碼后,接收端第個子載波上的接收符號為

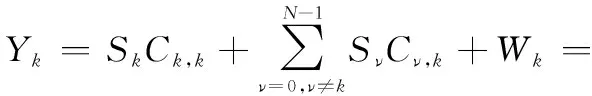
(,+-1,2,-1++1,1,+1)+

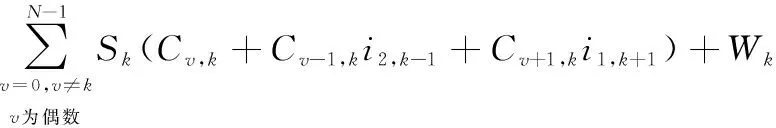
(12)

編碼后的ICI系數可定義為

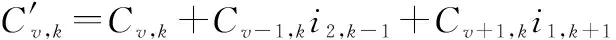
(13)

與傳統OFDM系統的編碼矩陣相比,FrFT-OFDM自消除矩陣參數設計的突出問題在于ICI系數相鄰項的相位差值問題,若無法將相鄰項的相位統一則對ICI的削弱效果有限,且當鄰項相位相反時甚至可能增強ICI,由此編碼矩陣參數不僅需考慮幅值因素也應考慮相位因素。

分析式(7)中,的表達式不難發現,鄰項ICI系數,與+1,之間的相位差近似滿足

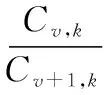
(14)

則自消除矩陣參數滿足

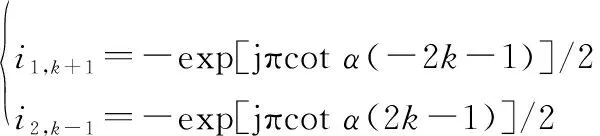
(15)

式(15)可以很大程度上修正ICI系數鄰項之間的相位差,從而更有效地抵消,,實現對ICI的抑制。

經過ICI自消除編碼后的第個子載波的CIR可表示為

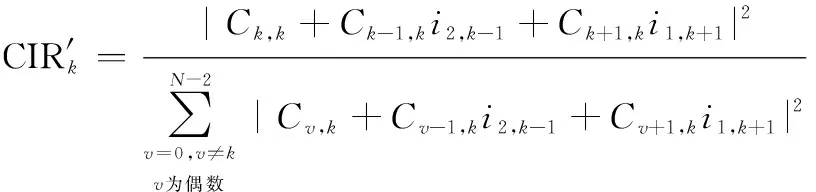
(16)

當=π2時,系統退化為經典OFDM系統,代入式(15)與式(16)可得

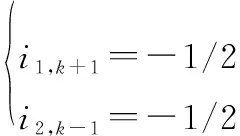
(17)

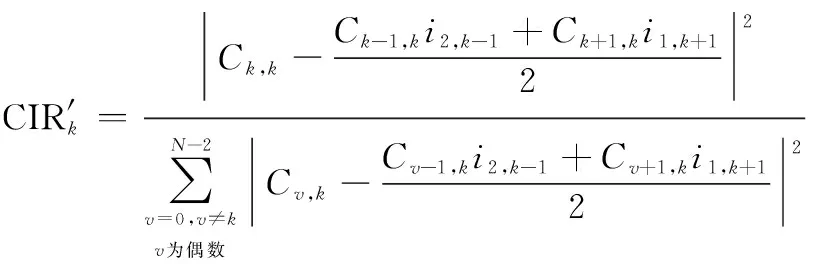
(18)

此時,設計的自消除編碼矩陣與CIR計算式與1/2編碼效率的ZH算法完全相同,即可認為本文所提出自消除編碼方案為ZH算法的一種推廣形式。

與ZH算法相比,本文方案的自消除矩陣參數設計時考慮了相位因素的影響,在參數計算過程中提升了運算量,若FrFT-OFDM系統的旋轉角度保持不變,則只需計算一次編碼矩陣,而編碼過程的計算復雜度與ZH算法相同,則本文算法相較于ZH算法的運算量提升十分有限。

2.2 頻率偏移補償

傳統OFDM系統的子載波為指數信號,不存在因時延而產生的等效頻偏,Δ完全由Δ產生,系統無法通過調整自身結構削弱受到的Δ;而FrFT-OFDM系統得益于FrFT旋轉角度可調的特性,可通過選擇適宜的旋轉角度,將Δ作為頻率偏移補償抵消Δ,降低Δ以達到有效抑制ICI的目的。

在進行頻率補償時,因為各徑的時延區別,引入的頻率補償并不能使每條徑上的Δ均為0,若調整角度引入的頻率補償值過大,則可能在部分徑上產生逆向頻率偏移,反而增強ICI。由此在選擇旋轉角度的過程中,應使引入的頻率補償不會在任一徑上產生逆向頻偏,則應滿足關系

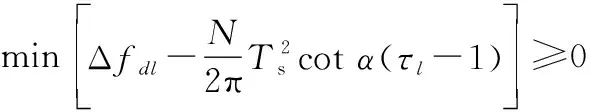
(19)

為了使式(19) 成立,旋轉角度搜索范圍應滿足

∈[, π-]

(20)

式中:可表示為

(21)

若信道中僅存在一徑,當旋轉角度取式(20)所示區間某一邊界時,該徑的Δ降至0,系統ICI完全消除,此旋轉角度即為最佳旋轉角度;若存在多徑時,由于多徑傳輸的復雜性,的選擇受到各徑參數的影響,需要在搜索區間內對旋轉角度進行遍歷,搜索使系統具有最優抗干擾性能的旋轉角度。

在傳統的ICI消除研究中,多以傳遞有用信號的子載波的CIR均值作為系統抗干擾能力的度量標準,然而在時頻雙選衰落信道環境下,FrFT-OFDM系統在部分旋轉角度上CIR均值較高而方差很大,部分CIR低的子載波即使在無噪環境下也可能因ICI出現錯誤判決進而產生誤碼,系統會產生嚴重的地板效應。因此,本文從有效削弱系統地板效應的目的出發,提出了新的抗干擾性能度量標準,即對CIR值較低的一半子載波求取均值,則此時最優旋轉角度搜索方案步驟如下。

設起始旋轉角度=,搜索步長為;

以為旋轉角度計算每個子載波上的CIR值;

對CIR值進行從小到大排序,由數值從低到高取2項,并求取均值CIR,若=0,則CIR_min=CIR,=;否則,直接進入步驟4;

若CIR_min≤CIR,CIR_min=CIR且=;否則,維持CIR_min與不變;

=+,若>(π-),直接進入步驟6;否則,跳轉至步驟2;

輸出CIR_min與。

若信道為快速時變衰落信道,需對信道變化進行快速追蹤,可將本文算法同文獻[8]和文獻[20]等文中提出的快速算法相結合,在保證計算精度的前提下降低算法的運算量。

3 仿真結果分析

為了驗證本文提出的ICI自消除方案對FrFT-OFDM系統誤碼率性能的提升效果,需要對其進行仿真驗證。在仿真過程中,設置FrFT-OFDM系統的子載波個數為64,調制方式為BPSK,符號周期為8 μs;假設信道為4徑傳播模型,其中各徑的延遲分別為{0,,2,3},平均功率相同,最大頻率偏移Δ max=01。

圖6為采用12編碼效率的本文方案、ZH方案、鄰數據取反方案、對稱數據取反方案的自消除FrFT-OFDM系統以及經典FrFT-OFDM系統在不同信噪比條件下的誤碼率比較,旋轉角度為本文方案搜索所得最優角度。從圖6中可以直觀地看出,在所有方案中,本文方案的誤碼率性能最優,而其他方案相較于經典FrFT-OFDM系統雖有一定的改善但是誤碼率性能的提升都十分有限,且在高信噪比條件下,會產生較為明顯的地板效應。

圖6 不同自消除編碼方案誤碼率比較Fig.6 Comparison of BER among different self-cancellation schemes

圖7為1/2編碼效率的本文方案、1/2編碼效率的自消除編碼OFDM系統(即=π/2)和通過所有子載波上CIR均值搜索最優角度的1/2編碼效率的傳統方案在不同信噪比條件下的誤碼率比較。由前文分析可知,接收信號的分數域表示中包含期望信號、ICI信號和信道噪聲3部分,接收端能否正確判決出接收符號受ICI信號和信道噪聲的影響,當信噪比較低時,噪聲對判決結果的影響較強,3種方案受較強的噪聲與時頻雙選衰落所產生的ICI的共同作用誤碼率性能均較差。而隨著信噪比的逐步上升,噪聲的影響逐漸減小,ICI對判決結果的影響增強。由圖7曲線可知,自消除編碼OFDM和傳統方案FrFT-OFDM未能有效抑制ICI,均產生了相對明顯的地板效應。雖然自消除OFDM表現相對較好,但當誤碼率達到5×10左右也無法再提高性能。而由本文所提出的旋轉角度篩選方案限制各子載波上極低CIR值的出現,有效抑制了地板效應,相較于其他兩種方案提升了系統性能。

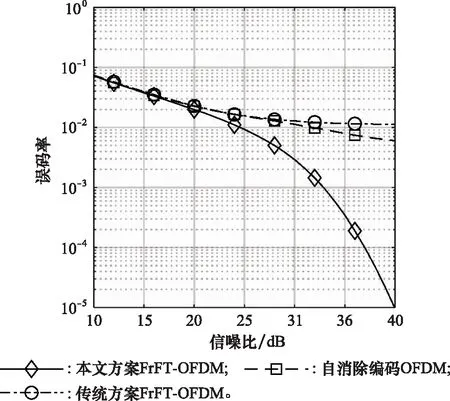
圖7 不同旋轉角度自消除FrFT-OFDM系統誤碼率比較Fig.7 Comparison of BER among self-cancellation FrFT-OFDM with different rotation angles

圖8顯示了不同編碼效率本文方案的誤碼率性能。從3種編碼效率下的誤碼率曲線可以看出,隨著編碼效率的提升,系統對復雜信道環境的適應能力下降,誤碼率性能逐漸降低,但是即使在較高編碼效率下,本文方案仍未呈現出明顯的地板效應。

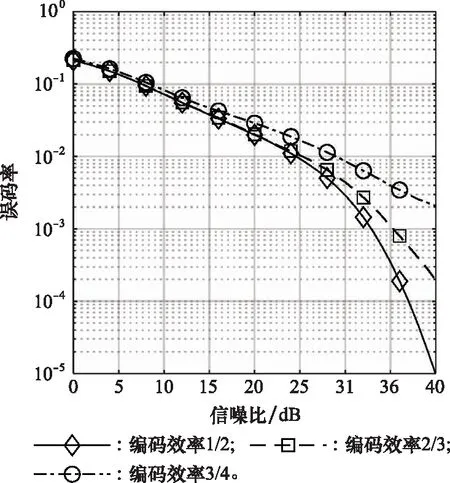
圖8 不同編碼效率與本文方案誤碼率比較Fig.8 Comparison of BER between the proposed scheme with different coding efficiencies

4 結 論

在OFDM系統的自消除方案的基礎上,本文提出了一種適用于FrFT-OFDM系統的ICI自消除方案,改進了傳統OFDM系統自消除編碼矩陣的參數設計方案并與頻率補償方案相聯合,為更好地抑制ICI提供了平臺。實驗仿真證明,相較于ZH方案、鄰數據取反方案和對稱數據取反方案,本文所提出的帶有相位補償的自消除編碼矩陣更適用于FrFT-OFDM系統,在相同的編碼效率下有著更好的誤碼率性能,且本文編碼矩陣可靈活設置編碼效率。此外,本文提出的面向復雜信道的抗干擾性能度量標準,充分利用FrFT-OFDM系統旋轉角度可變的結構優勢,篩選最優旋轉角度以適應不同的信道環境,有效抑制ICI,提升系統的通信性能。