云化虛擬化網(wǎng)絡業(yè)務可用度多參數(shù)敏感性分析

朱 杰, 黃 寧, 程 亮

(1. 北京航空航天大學可靠性與系統(tǒng)工程學院, 北京 100191; 2. 北京航空航天大學云南創(chuàng)新研究院, 云南 昆明 650233; 3. 華為技術有限公司數(shù)據(jù)通信產(chǎn)品線, 北京 100191)

0 引 言

云化虛擬化網(wǎng)絡(network function virtualization, NFV)業(yè)務是通過對軟硬件節(jié)點提供服務組合而達到對外提供使用的某種綜合能力,業(yè)務可用度是業(yè)務能夠提供使用的能力;對NFV網(wǎng)絡業(yè)務可用度進行參數(shù)敏感性分析從而找到關鍵參數(shù)是當前網(wǎng)絡運營商為了提高業(yè)務可用度亟需解決的一個問題。NFV業(yè)務可用度的影響因素眾多,某些因素的小幅度變化很可能導致業(yè)務的可用度發(fā)生較大的變化,極具不確定性。所以,以高業(yè)務可用度為目標對網(wǎng)絡業(yè)務進行優(yōu)化的前提就是要找到影響業(yè)務可用度的因素。現(xiàn)有研究表明,網(wǎng)絡中的設計參數(shù)眾多,既有異類的參數(shù)也有相同類別不同構件的參數(shù)。異類的參數(shù)是指網(wǎng)絡中不同屬性的參數(shù),如某一類節(jié)點的平均故障間隔時間、故障檢測時間、故障檢測概率等等;同類別的參數(shù)是指網(wǎng)絡中不同位置的具體構件的某個相同屬性的參數(shù),如D1的平均故障間隔時間(D1-α)、D2的平均故障間隔時間(D2-α)、…、D的平均故障間隔時間(D-α)均為同一類別的參數(shù)。在基于網(wǎng)絡演化模型的業(yè)務可用度仿真輸入中,只可以對相互獨立的異類的參數(shù)進行設置,同類別參數(shù)由于其耦合關系,在仿真過程中取值相同。所以,通過仿真的輸入與輸出僅能對異類參數(shù)進行分析;而同類別的參數(shù)就必須根據(jù)網(wǎng)絡演化過程中業(yè)務具體的路由變化過程進行分析。

敏感性分析就是通過不斷改變模型的參數(shù)輸入組合方式,對模型輸出結果分析得到參數(shù)的敏感性排序,找到對模型輸出結果影響最大的關鍵參數(shù)。當前的敏感性分析方法主要分為局部敏感性分析方法和全局敏感性分析方法。局部敏感性分析是控制模型中其他參數(shù)的取值不變,僅通過不斷改變所研究的參數(shù),分析該參數(shù)的敏感性。Carpio等和Rui等分別采用基于RBD和基于Petri網(wǎng)的NFV業(yè)務可用度的參數(shù)局部敏感性分析方法分析了虛擬網(wǎng)絡功能(virtual network function, VNF)的遷移時間的敏感性,該方法將網(wǎng)絡中構件的MTBF 和MTTR看作定值,通過不斷改變遷移時間的取值得到其敏感性,得到的參數(shù)的敏感性僅能在其余參數(shù)保持不變的情況下成立,其分析結果在所有參數(shù)的整個取值空間內(nèi)并不準確。全局敏感性分析方法可以同時分析多個參數(shù)共同變化時對模型輸出結果的影響,并對各參數(shù)進行敏感性排序,但是其前提是假設模型中的參數(shù)相互獨立而且所需樣本量多。Steiner等提出了基于最小二乘支持向量回歸的全局敏感性分析方法,該方法其原理是事先假設模型的基本數(shù)學形式,使用原模型的輸入和輸出數(shù)據(jù)進行擬合構建出數(shù)學代理模型,利用代理模型分析各個參數(shù)的敏感性。其他常用的全局敏感性分析方法如篩選方法、響應曲面法、傅里葉振幅敏感性檢驗法、互信息指數(shù)法等也都假設參數(shù)獨立采用了構建代理模型的思想,在構建代理模型的過程中往往需要大量的仿真樣本。NFV網(wǎng)絡設備類型多參數(shù)種類多,而且業(yè)務之間因為共享網(wǎng)絡資源而相互耦合,既無法事先假設代理模型的基本形式,也無法通過大量的仿真樣本擬合出數(shù)學代理模型。主效應圖在局部敏感性分析的方法上進行全局性改進,可以分析參數(shù)在多個局部內(nèi)與模型輸出結果的關系,通過改變單個設計參數(shù)的水平,用每個水平與其他參數(shù)的所有可能的組合對結果影響的平均值進行擬合畫圖,該方法可以不用構建代理模型,通過比較不同參數(shù)主效應圖驗證參數(shù)對模型輸出結果的影響是否明顯,但是該方法得到的結果只是多個局部的平均值,不能對相互耦合的同類設備的同類參數(shù)進行敏感性分析,而且所需要的仿真樣本數(shù)與參數(shù)數(shù)量呈指數(shù)增長關系。因此,已有的全局敏感性分析方法也不能支持NFV網(wǎng)絡業(yè)務可用度多參數(shù)的敏感性分析。

針對以上背景,本文提出一種基于網(wǎng)絡演化模型的多因素敏感性分析方法,直接通過網(wǎng)絡演化模型的輸入輸出對影響網(wǎng)絡業(yè)務可靠性的各種異類參數(shù)進行敏感性分析,找出影響最大、最敏感的主要參數(shù)類別;進一步提出基于動態(tài)業(yè)務介數(shù)的方法,分析同類別不同設備的參數(shù)的敏感性,找到關鍵的同類不同設備參數(shù)。本研究既可以克服局部敏感型分析方法結果在全局范圍內(nèi)不準確的缺點,也可以通過盡量少的仿真樣本量保證找到的關鍵設備參數(shù)的正確性。既可以支持具有參數(shù)相互耦合特點模型的敏感性分析,拓展敏感性分析方法，還能對不同設備類型不同種類參數(shù)的敏感性進行分析,找出業(yè)務可用度的敏感性參數(shù),支持以高業(yè)務可靠性為目標的網(wǎng)絡業(yè)務優(yōu)化,具有重要的實際應用價值。

1 NFV網(wǎng)絡參數(shù)敏感性分析方法

NFV網(wǎng)絡中采用了網(wǎng)絡功能虛擬化技術和云計算技術使得傳統(tǒng)網(wǎng)絡的單一軟硬件系統(tǒng)變?yōu)槎鄠€網(wǎng)元共享的軟硬件平臺,網(wǎng)絡系統(tǒng)的故障類型與故障發(fā)生后的動態(tài)變化更加復雜。隨著網(wǎng)絡業(yè)務路由的智能動態(tài)調整,業(yè)務可靠性會受到整網(wǎng)構件的設計參數(shù)(如平均故障間隔時間、故障維修時間、故障檢測率等等)的影響,當網(wǎng)絡中多業(yè)務同時運行時,業(yè)務重路由以及遷移倒換導致業(yè)務對網(wǎng)絡資源的競爭也會對網(wǎng)絡業(yè)務的可用度造成影響。與此同時,網(wǎng)絡中任何一個參數(shù)的調整均會導致整網(wǎng)的業(yè)務可用度發(fā)生改變。網(wǎng)絡中影響業(yè)務可靠性的因素眾多,并且由于業(yè)務路徑的耦合作用使得不同構件的參數(shù)之間也存在相互耦合關系,用現(xiàn)有的網(wǎng)絡演化模型對業(yè)務用度進行分析的過程中,忽略任何一個參數(shù)都有可能對其造成嚴重的影響。因此，針對網(wǎng)絡中參數(shù)耦合的特點,對影響NFV網(wǎng)絡業(yè)務可用度參數(shù)的敏感性進行分析,分析方法主要從相互獨立的異類參數(shù)和相互耦合的同類參數(shù)兩個方面進行,最終找到關鍵參數(shù)。本文所用到的網(wǎng)絡構件及相關參數(shù)的表示符號如表 1所示，用“設備符號-參數(shù)符號”表示某一類設備的某個參數(shù)。

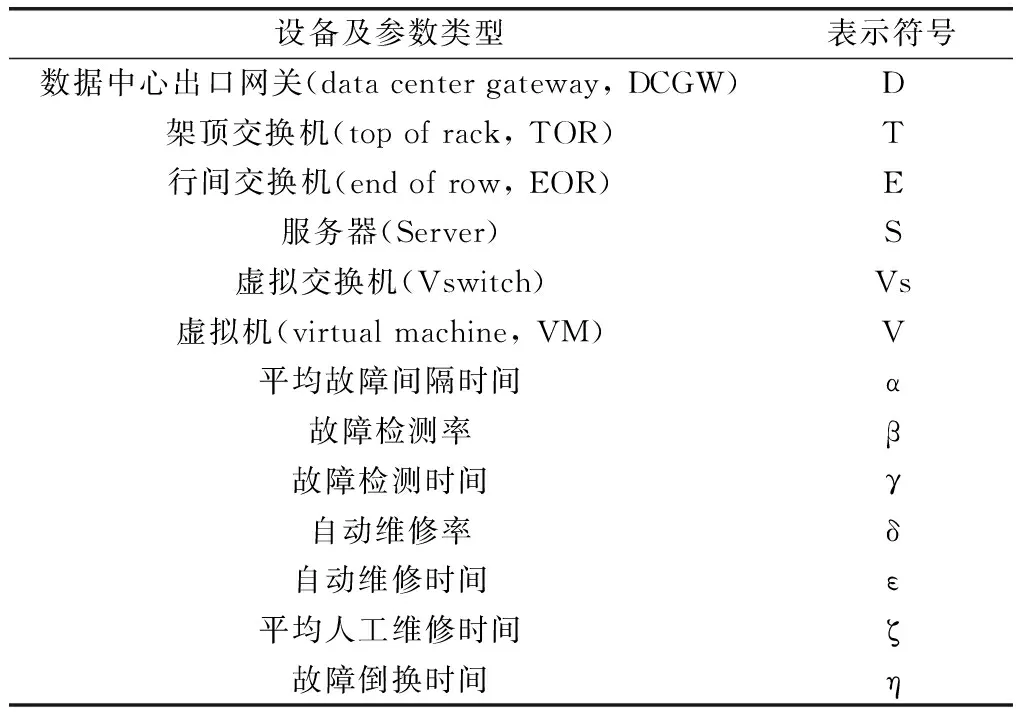
表1 本文用到的設備、參數(shù)及其表示符號

1.1 NFV網(wǎng)絡建模與仿真

對NFV網(wǎng)絡中影響業(yè)務可用度參數(shù)的敏感性進行分析,首先需要找到網(wǎng)絡中有哪些參數(shù)可能會對業(yè)務可用度造成影響,并利用這些參數(shù)通過對網(wǎng)絡的建模與仿真計算出業(yè)務可用度。根據(jù)VNF可用度設計的要求,影響業(yè)務可用度的設計參數(shù)分為3層:VNF層為了實現(xiàn)故障快速倒換需要合理設計倒換時間和故障檢測時間;虛擬化層為了及時發(fā)現(xiàn)故障需要合理設計故障自動檢測時間、平均故障間隔時間和故障自動恢復時間;硬件層為了保證功能需要設計合理的平均故障間隔時間、故障檢測及上報時間。根據(jù)華為《NFV網(wǎng)絡可用度需求報告》,影響業(yè)務可用度的虛擬化設備(軟件)設計參數(shù)主要如圖1所示。

圖1 NFV網(wǎng)絡部分構件設計參數(shù)Fig.1 Design parameters of NFV network components

本文主要基于網(wǎng)絡演化模型對NFV網(wǎng)絡業(yè)務可用度進行建模與仿真,網(wǎng)絡演化模型是通過建立網(wǎng)絡系統(tǒng)以及故障發(fā)生時的系統(tǒng)應對來表征網(wǎng)絡系統(tǒng)的動態(tài)演化過程的模型,包括3部分內(nèi)容:網(wǎng)絡演化對象、網(wǎng)絡演化條件和網(wǎng)絡演化規(guī)則。

網(wǎng)絡演化對象是為需要評估可用度的NFV網(wǎng)絡建立的模型,包括兩部分內(nèi)容:基礎設施層(節(jié)點信息、鏈路信息)和業(yè)務層(業(yè)務信息、VNF信息和服務部署信息)。

網(wǎng)絡演化條件表達了誘發(fā)NFV網(wǎng)絡無法提供對業(yè)務支持的條件,根據(jù)目前華為的初步需求,演化條件包括:演化對象中任意一個節(jié)點出現(xiàn)故障(動態(tài)變化)、 演化對象中任意一個節(jié)點故障修復等。

網(wǎng)絡演化規(guī)則回答出現(xiàn)不同類型故障時網(wǎng)絡系統(tǒng)是如何運轉的,主要包括:交換機狀態(tài)發(fā)生變化、Server節(jié)點狀態(tài)變化、Vswitch節(jié)點狀態(tài)變化、VM節(jié)點狀態(tài)發(fā)生變化。

1.2 仿真實驗設計方法

找到網(wǎng)絡中可能會對業(yè)務可用度造成影響的參數(shù)后,進一步將參數(shù)進行不同的取值組合設計大量的仿真試驗,再根據(jù)仿真的結果來分析計算各類參數(shù)的敏感性指標。其重點就是如何設計大量的仿真試驗,即各參數(shù)的取值應該如何設置才能用最少的仿真試驗得到準確的敏感性分析結果。最優(yōu)拉丁方設計是常用的實驗設計方法,是在拉丁方設計的基礎上,改進其均勻性,使得參數(shù)和響應的擬合更加精確,具有更好的空間填充性和均衡性,其能用盡可能少的試驗設計點表示盡可能多的信息。最優(yōu)拉丁方設計方法是常用的敏感性分析試驗設計方法,其主要分為兩步。

(1) 采樣:對每個輸入隨機變量進行取值空間內(nèi)的隨機采樣,確保采樣點能夠均勻覆蓋在整個區(qū)間內(nèi)。

最優(yōu)拉丁方采樣是在個參數(shù)的模型中,將每個參數(shù)的設計空間均勻地等分為個小區(qū)間,在每個小區(qū)間內(nèi)隨機選取一個點,共組成個點,保證一個參數(shù)的每個水平只被研究一次,構成一個具有維空間,樣本數(shù)為的拉丁方設計,記為×LHD,如下矩陣所示。

(2) 排列:改變每個隨機變量采樣值的排列順序,確保相互獨立的隨機變量采樣值之間的相關性最小。

將第一步采樣中得到的×維矩陣記為,中的各列可能隨機引起了一定的統(tǒng)計相關,這會影響模擬結果。為了減少這種相關性,Florian 提出基于斯伯爾曼系數(shù)描述矩陣中各列間的統(tǒng)計相關,定義為

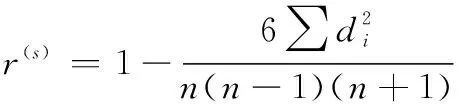
(1)

式中:斯伯爾曼系數(shù)()∈[-1,1];為兩樣本的序差;為樣本數(shù)。

假設初始樣本矩陣中每個元素值的序號位置描述為×的矩陣,再用序相關矩陣來描述矩陣每列間的統(tǒng)計相關,其中(,=1,2,…,) 是矩陣的第列和第列之間的斯伯爾曼系數(shù),可知是對稱矩陣,且矩陣各列都不相關時,矩陣為單位矩陣。僅考慮正定矩陣時的情況,用Cholesky分解把矩陣表述成

=

(2)

式中:是下三角矩陣。再進行如下變換:

=

(3)

式中:=。

再用序相關矩陣來描述每列之間的統(tǒng)計相關。此時,矩陣比矩陣更加接近于單位矩陣。根據(jù)對矩陣重新排序,得到輸入矩陣即為排列后的輸入矩陣。

根據(jù)敏感性分析要求,選擇合理的參數(shù),并在各個參數(shù)的取值范圍內(nèi)利用最優(yōu)拉丁方實驗設計方法設計兩組容量分別為的輸入樣本矩陣。若要設置更多的樣本矩陣,其實就是分析更多的情況,等價于增加樣本量的值。的取值越大,矩陣能夠覆蓋的情況越多,分析的結果也越準確。因此,對于的確定,應該在計算能力與計算時間接受的范圍內(nèi),將設得盡可能大。如果確定的輸入變量參數(shù)共有個,每個參數(shù)都有自己的初始設計空間,首先在各個空間內(nèi)采用最優(yōu)拉丁方采樣2次,并進行排序,可得到下列兩個樣本矩陣:

1.3 基于全效應指數(shù)的異類參數(shù)敏感性指標

有了足夠的輸入與業(yè)務可用度輸出樣本后,采用合理的方法對結果進行分析,得到參數(shù)的敏感性指標是敏感性分析的關鍵。本文主要采用基于蒙特卡羅積分的Sobol指數(shù)法,其基本思想是分析輸入對輸出方差的影響。假設一組輸入變量的值,利用該輸入變量求得輸出和輸出的條件方差,輸出的非條件方差與條件方差的差異就反映了該輸入變量對模型輸出結果的影響。該方法的主要分析過程如下:

把,中的第列互換,其他項不變,得到新的樣本矩陣,如下：

交換矩陣和中的一列,對于矩陣中的某一行來說也是僅僅改變了一個參數(shù)值,但是對于整個矩陣來說,是在種情況下改變該參數(shù)的值,當?shù)娜≈祲虼髸r,就可以表示該參數(shù)在所有情況下對結果的影響。將各組參數(shù)樣本帶入到網(wǎng)絡演化模型中,可算得對應的業(yè)務可用度仿真結果,輸出相應的方差和參數(shù)敏感性指標分別為

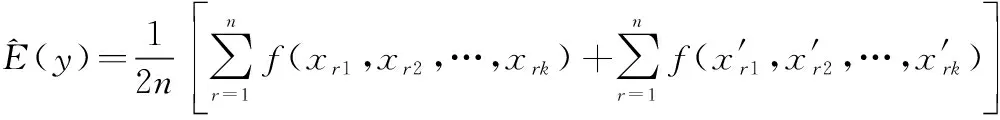
(4)

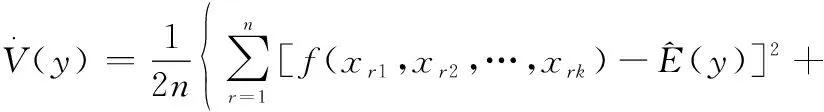
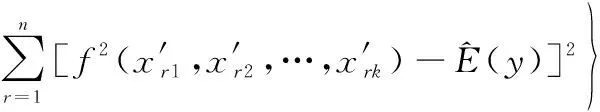
(5)

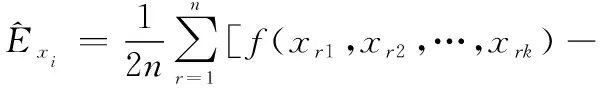
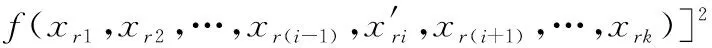
(6)

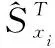
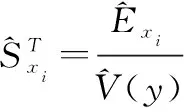
(7)

全效應指數(shù)描述了對輸出的影響,其值在0 到1 之間。若一個變量的全效應指數(shù)很小,表明該變量不僅自身的變動對輸出的影響小,而且該變量與其他變量之間的交互效應也很小。因此，考慮對全效應指數(shù)小的變量取固定值,可以使模型的輸入變量減少,達到簡化模型的目的。用上述方法計算所要分析的變量參數(shù)的全效應指數(shù),全效應指數(shù)越大,則該參數(shù)變量對模型輸出結果的影響越大。

1.4 基于動態(tài)業(yè)務介數(shù)的同類參數(shù)敏感性指標

前一節(jié)中Sobol指數(shù)法可以找到關鍵參數(shù)類別,但是該參數(shù)為一類設備參數(shù),如云化虛擬化網(wǎng)絡中的TOR的節(jié)點故障間隔時間,但是網(wǎng)絡中TOR的數(shù)量遠不止一個,當網(wǎng)絡中有多業(yè)務存在時,由于業(yè)務動態(tài)路由導致的業(yè)務耦合,使得網(wǎng)絡中所有的TOR并不等效。所以云化虛擬化網(wǎng)絡中不同位置的TOR對業(yè)務可靠性造成的影響不同。為了分析在多業(yè)務耦合下的不同設備的某一屬性參數(shù)(同類參數(shù))的敏感性,我們提出了節(jié)點動態(tài)業(yè)務度的概念。

在NFV網(wǎng)絡中,由于業(yè)務重路由的影響,節(jié)點和鏈路中承載的業(yè)務時刻在發(fā)生變化,難以直接分析出某個具體的設備參數(shù)的敏感性。但是在網(wǎng)絡運行過程中,某節(jié)點承載的業(yè)務越多,則當該節(jié)點發(fā)生故障時就會造成更多業(yè)務的故障,從而對整網(wǎng)的業(yè)務可靠性造成更大的影響。因此,我們提出了動態(tài)業(yè)務介數(shù)的概念,通過動態(tài)業(yè)務介數(shù)這個指標來分析節(jié)點的敏感性。

節(jié)點動態(tài)業(yè)務介數(shù):指在網(wǎng)絡工作的整個區(qū)間內(nèi),節(jié)點承載過的業(yè)務的累積量。若同一業(yè)務在不同的工作路徑下都經(jīng)過某一條節(jié)點,則該節(jié)點的動態(tài)業(yè)務介數(shù)增加1。下面以一個具體的過程進行說明,如圖2所示。

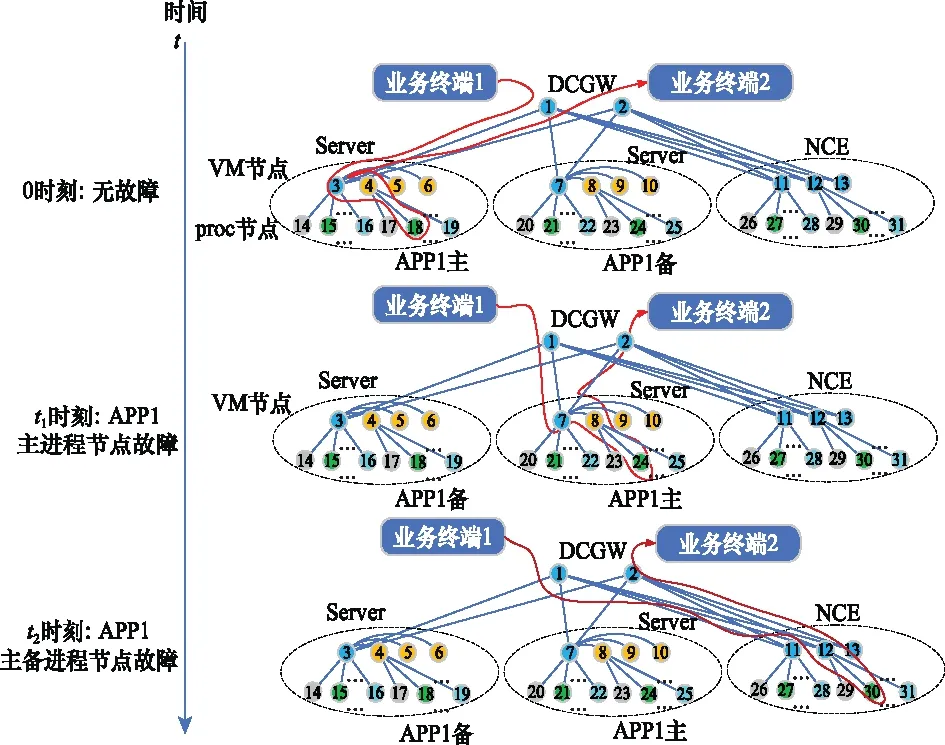
圖2 云化網(wǎng)絡演化過程Fig.2 Evolution of NFV

0時刻:網(wǎng)絡中無節(jié)點故障,業(yè)務部署在節(jié)點1—3—18—4—1上;

時刻:網(wǎng)絡中APP1主進程節(jié)點18故障,業(yè)務切換到備用進程節(jié)點24上,同時主進程節(jié)點降為備進程節(jié)點,備進程節(jié)點升為主進程節(jié)點,此時業(yè)務的路徑為:1—7—24—8—2。

時刻:網(wǎng)絡中APP1主、備進程均故障,業(yè)務遷移到備用資源池NCE中,此時業(yè)務的工作路徑為:1—12—30—12—2。直至工作任務結束。

在這整個過程中,按照動態(tài)業(yè)務介數(shù)的定義可以知道:節(jié)點1的動態(tài)業(yè)務介數(shù)為3;節(jié)點2的動態(tài)業(yè)務介數(shù)為2;節(jié)點3、18、4、7、24、8、12、30的業(yè)務動態(tài)介數(shù)為1。

由于節(jié)點動態(tài)業(yè)務介數(shù)的仿真也需要考慮不同的設計參數(shù)組合情況,因此在計算節(jié)點的動態(tài)業(yè)務介數(shù)時,需要運用第2.2節(jié)中的仿真實驗設計方法設計多組試驗。在每一組實驗中,僅需在網(wǎng)絡演化模型的程序里增加一個動態(tài)業(yè)務介數(shù)的統(tǒng)計值變量,節(jié)點上初始部署的業(yè)務數(shù)量為節(jié)點動態(tài)業(yè)務介數(shù)的初始值;當節(jié)點發(fā)生故障,業(yè)務進行遷移或者倒換后,業(yè)務新的路由上所有節(jié)點的動態(tài)業(yè)務介數(shù)增加1。

1.5 整網(wǎng)參數(shù)敏感性排序

采用上述方法得到了異類和同類參數(shù)的敏感性指標后,如何才將二者結合起來對整網(wǎng)的所有參數(shù)進行敏感性排序？本文提出了一種新的敏感性指標,若通過敏感性分析,得到的各類參數(shù)的全效應指數(shù)以及各個節(jié)點的動態(tài)業(yè)務介數(shù)分別如表2所示。網(wǎng)絡中某一個具體設備的某個參數(shù)的敏感度,不僅與該類參數(shù)的全效應指數(shù)相關,更與該設備上部署的業(yè)務數(shù)量密切相關。所以,為了描述網(wǎng)絡中具體設備的具體參數(shù)的敏感度,我們將全效應指數(shù)與節(jié)點動態(tài)業(yè)務介數(shù)結合起來,用該類參數(shù)的全效應指數(shù)與某一個構件的動態(tài)業(yè)務介數(shù)所占比例的乘積作為該構件上具體參數(shù)的敏感度。則網(wǎng)絡中所有參數(shù)的敏感度計算方法如表2所示,各參數(shù)的敏感度進行大小排序,即可得到整網(wǎng)中的參數(shù)。

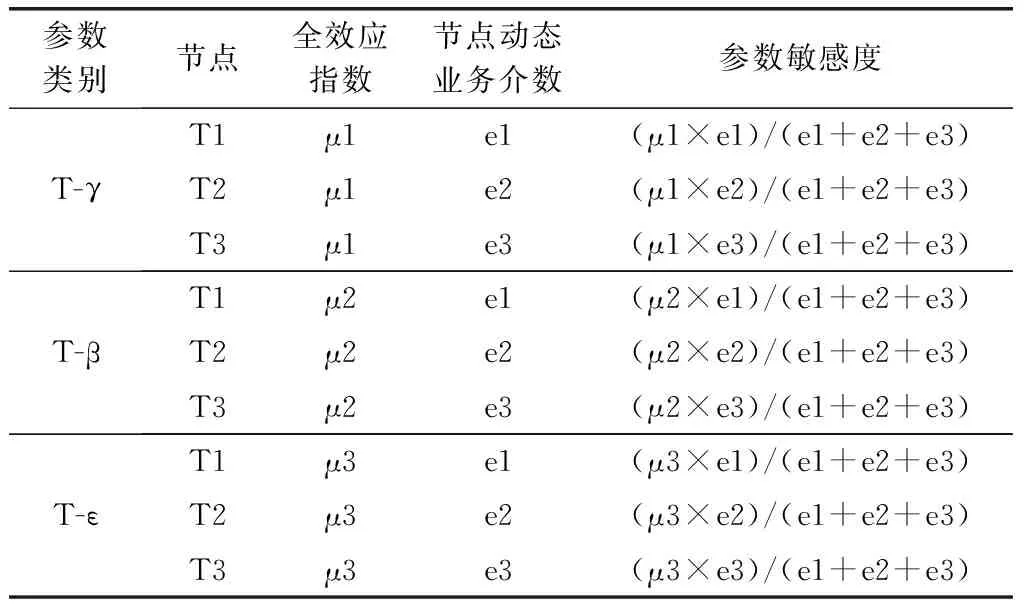
表2 具體構件的參數(shù)敏感度計算方法

2 案例分析

2.1 案例介紹

根據(jù)NFV網(wǎng)絡架構特點,本文構建了一個典型的NFV網(wǎng)絡案例如圖3所示。該案例中共有各種類型的節(jié)點28個,鏈路28條,網(wǎng)絡拓撲為樹狀。在該網(wǎng)絡上部署了兩個業(yè)務,業(yè)務的工作路徑可在圖3中看到。網(wǎng)絡中各節(jié)點的故障及修復參數(shù)信息如表3所示。本文的仿真平臺采用 Intel Corei7-3520 2.90 GHz CPU。

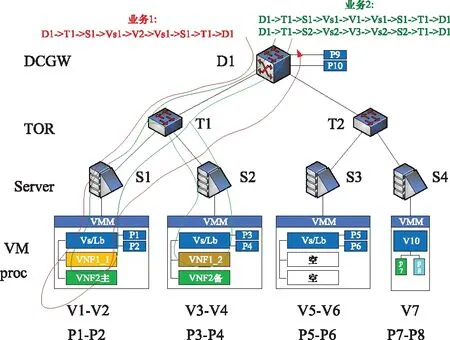
圖3 云網(wǎng)絡分析案例Fig.3 Case of the NFV

表3 fail_info欄數(shù)據(jù)內(nèi)容

2.2 網(wǎng)絡參數(shù)敏感性分析

(1) 網(wǎng)絡建模與仿真

根據(jù)上述案例,本文以整網(wǎng)業(yè)務平均可用度作為分析目標,根據(jù)表2確定的輸入?yún)?shù)類別并根據(jù)文獻[15]中NFV網(wǎng)絡可靠性要求對每一類參數(shù)確定一個試驗取值范圍如表4所示。

利用表4中的參數(shù)對NFV網(wǎng)絡進行建模與仿真的具體方法參考文獻[2],本文不再贅述。

表4 輸入?yún)?shù)的試驗取值空間

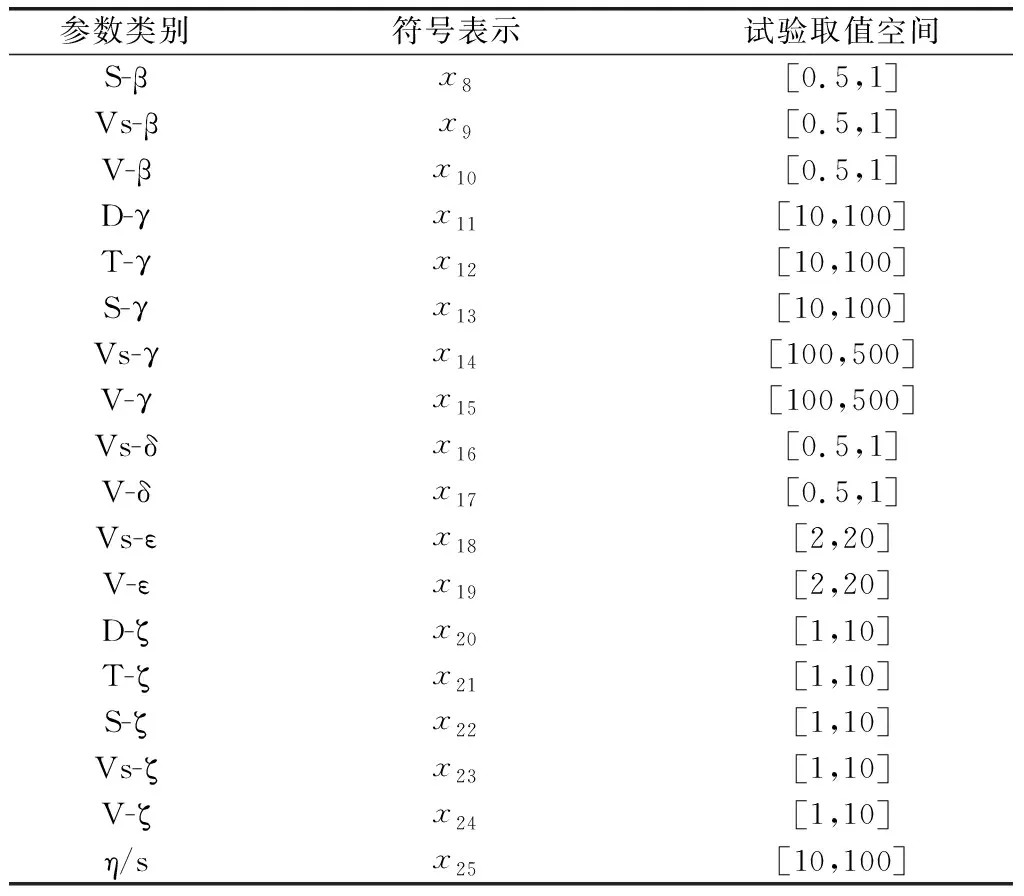
續(xù)表4

(2) 設計仿真實驗

利用第1.2節(jié)中介紹的最優(yōu)拉丁方實驗設計方法設計兩組容量為20的輸入矩陣(本文先擬定容量為20,之后再改變樣本容量,觀察參數(shù)排序是否穩(wěn)定)。其中一組輸入矩陣如所示。矩陣中每一行代表一個輸入樣本,每一列代表同一參數(shù)在不同樣本中的不同取值,用同樣的方法得到另外一組輸入矩陣。

=

將上述設計的輸入樣本矩陣和中的每一行輸入到網(wǎng)絡演化模型進行仿真,得到這一個輸入樣本矩陣的20組業(yè)務可靠度仿真結果如表5所示。由于網(wǎng)絡演化模型仿真時采用了蒙特卡羅抽樣,得到的網(wǎng)絡平均業(yè)務可用度具有一定的隨機誤差,所以本文分析將相同的參數(shù)輸入仿真100次,設置的仿真時長為200年,將100次整網(wǎng)平均業(yè)務可用度的均值作為這個輸入的模型輸出結果。這樣做的目的是減少敏感性分析過程中由于模型本身的隨機誤差對結果造成的影響。

表5 將A、B輸入到模型中得到業(yè)務可靠度值

(3) 異類參數(shù)敏感性指標計算

根據(jù)表5的仿真結果,可以分析出DCGW節(jié)點平均故障間隔時間的全效應指數(shù),計算過程如下:

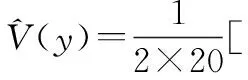
通過和中的輸入樣本和表5中得到的仿真結果,利用第13節(jié)中介紹的敏感性指標計算方法計算各類輸入?yún)?shù)的全效應,選出關鍵參數(shù)類別。得到的各類輸入?yún)?shù)的全效應及排序如表6所示。

表6 第一次異類敏感性分析得到的各類參數(shù)敏感性排序

由表6可以得到,Vswitch節(jié)點平均故障間隔時間、Vswitch節(jié)點自動維修概率、Vswitch節(jié)點平均人工維修時間這3類參數(shù)的全效應指數(shù)明顯跟其余參數(shù)的全效應指數(shù)不在一個量級,所以這3類參數(shù)為關鍵參數(shù)類別。上述分析均在樣本容量為20的情況下進行,為了保證樣本容量的取值滿足敏感性分析的要求,本文繼續(xù)在樣本容量為40、60、80的情況下分析,仿真試驗樣本均采用第1.2節(jié)的實驗設計方法進行設計。通過全效應指數(shù)的計算,得到的全效應結果如表7所示。

從表7中可以看到,雖然所有參數(shù)的全效應指數(shù)大小略有差異,但是3個關鍵參數(shù)類別的全效應指數(shù)與其余類別參數(shù)的全效應指數(shù)始終不在一個量級;而其余類別參數(shù)的排序稍微有所不同,造成這種現(xiàn)象的原因是其余參數(shù)類別的全效應指數(shù)較小,與3個關鍵參數(shù)類別不在同一量級,其結果更容易受到蒙特卡羅過程的影響,造成排序的不同,但是隨機誤差對關鍵參數(shù)類別的影響較小,所以關鍵參數(shù)類別的排序穩(wěn)定,結果可靠。

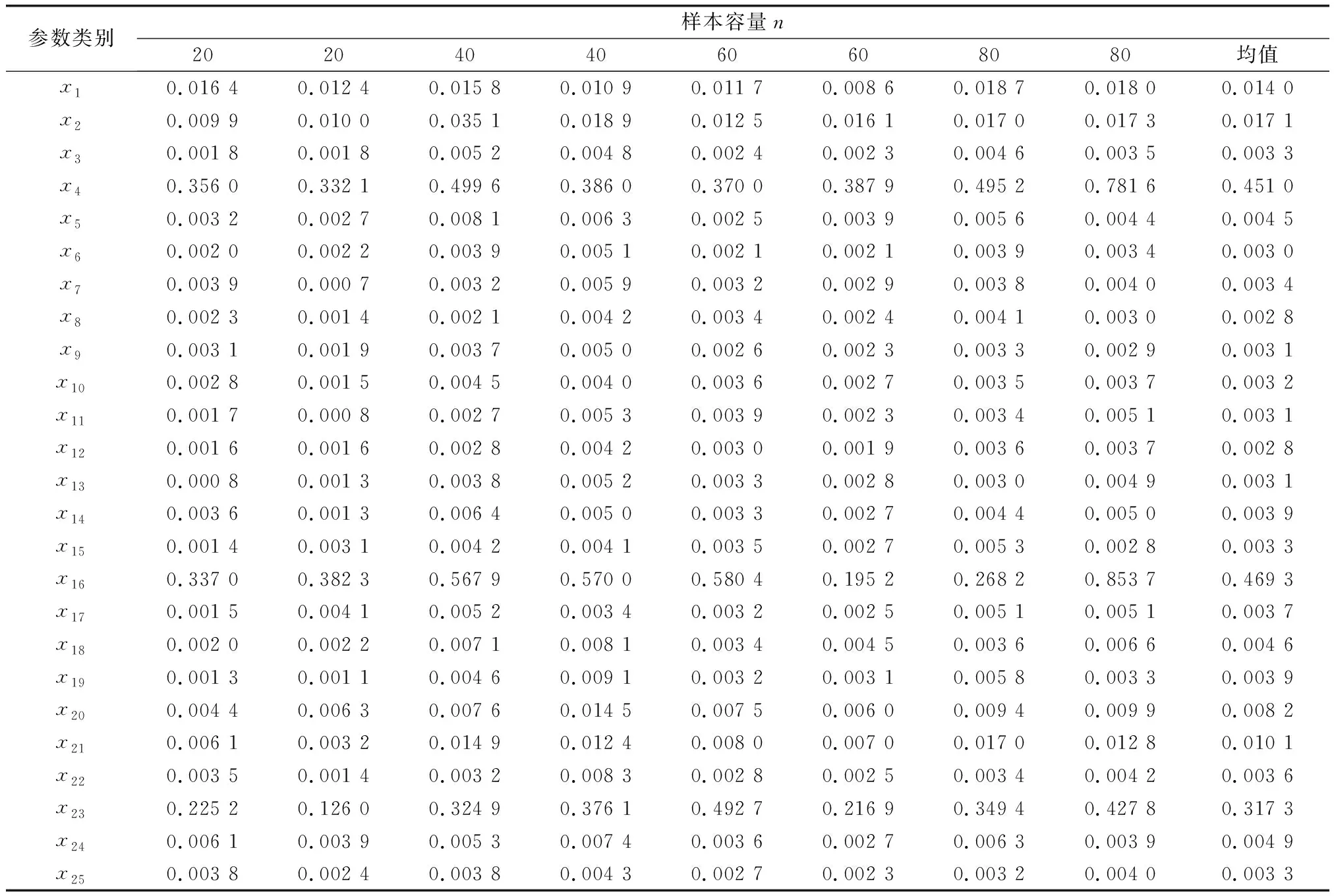
表7 不同樣本容量下的異類參數(shù)敏感性排序情況

(4) 同類參數(shù)敏感性指標計算

上一步找到的關鍵參數(shù)類別為:Vswitch節(jié)點平均故障間隔時間、Vswitch節(jié)點自動維修概率、Vswitch節(jié)點平均人工維修時間。由于關鍵參數(shù)類別與非關鍵參數(shù)類別的全效應指數(shù)不在同一個量級，因此同類參數(shù)的敏感性僅針對關鍵的參數(shù)類別進行。研究參數(shù)采用第1.2節(jié)中的試驗設計方法設計20組樣本,在每一個相同的樣本下進行10次仿真,對10次仿真的每個節(jié)點的動態(tài)業(yè)務介數(shù)取均值作為該樣本下的節(jié)點動態(tài)業(yè)務介數(shù)仿真結果;最后再將20個樣本得到的每個節(jié)點的動態(tài)業(yè)務介數(shù)取均值作為節(jié)點的最終動態(tài)業(yè)務介數(shù)。通過仿真,得到網(wǎng)絡中Vs1、Vs2、Vs3的動態(tài)業(yè)務介數(shù)如表8所示。

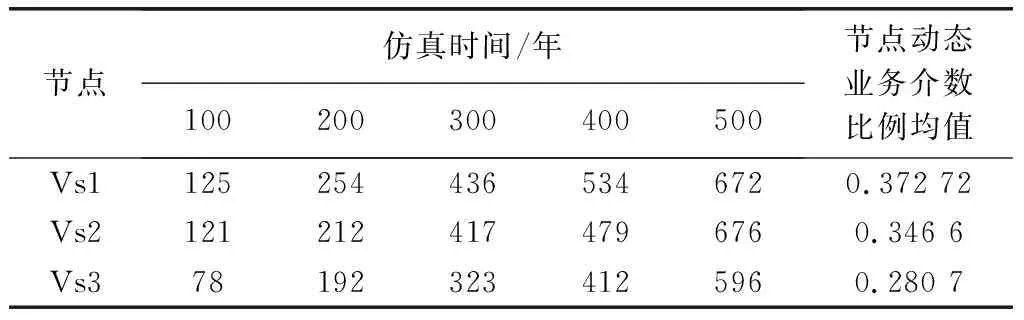
表8 不同仿真時間下的節(jié)點動態(tài)業(yè)務介數(shù)

由表8分析得到:隨著仿真時間的增加,節(jié)點的動態(tài)業(yè)務介數(shù)也隨之增加,但是Vs1 和Vs2的動態(tài)業(yè)務介數(shù)一直大于Vs3的動態(tài)業(yè)務介數(shù)。

(5) 網(wǎng)絡參數(shù)敏感性排序

由于NFV網(wǎng)絡中的節(jié)點異質,所以某一種節(jié)點的某一種屬性的參數(shù)可以稱為一類參數(shù)(如Vswitch節(jié)點平均故障間隔時間,它包括Vs1平均故障間隔時間、Vs2平均故障間隔時間、Vs3平均故障間隔時間3個參數(shù))。在相互獨立的參數(shù)類別的敏感性分析中,發(fā)現(xiàn)關鍵參數(shù)類別的全效應指數(shù)與非關鍵參數(shù)的全效應指數(shù)不在一個量級,所以關鍵參數(shù)只會在關鍵參數(shù)類中,因此可以僅進一步針對關鍵參數(shù)類別進行分析,找到關鍵參數(shù)。采用第1.5節(jié)中的具體網(wǎng)絡構件參數(shù)的敏感度計算方法,得到網(wǎng)絡參數(shù)的敏感度和敏感度排序如表9所示。

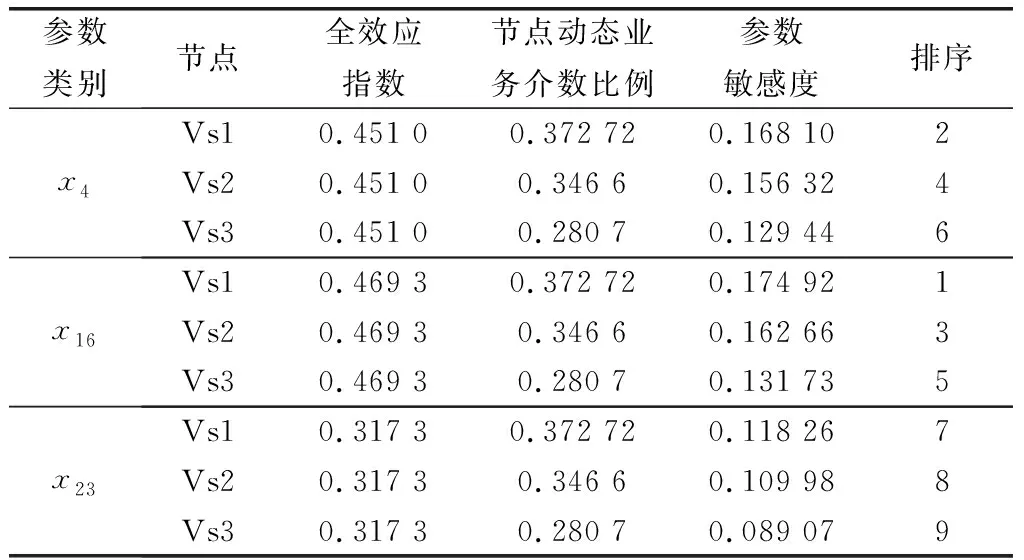
表9 具體構件的參數(shù)敏感度排序

根據(jù)表9得到的同類不同構件的參數(shù)的敏感度及排序,得到該案例中Top4的關鍵參數(shù)為Vs1設備自動維修概率、Vs1設備平均故障間隔時間、Vs2設備自動維修概率、Vs2設備的平均故障間隔時間。

3 對比分析

現(xiàn)有的敏感性分析方法只能對相互獨立的參數(shù)進行分析,所以在本文中我們先采用主效應圖的方法對相互獨立的參數(shù)類別進行分析,驗證找到的關鍵參數(shù)類別是否準確;進一步從NFV網(wǎng)絡的運行規(guī)則分析本文找到的具體的關鍵參數(shù)的合理性;最后對比兩種方法,說明本文所提方法在分析結果和仿真效率上的優(yōu)勢。主效應圖是通過對異類參數(shù)的局部敏感性取均值來衡量不同類別參數(shù)的敏感性,因此該方法并不能直接找到全局范圍內(nèi)的關鍵參數(shù)類別,但是可以用該方法從多個局部衡量本文找到的關鍵參數(shù)類別是否對模型結果有較大的影響。

以分析Vswitch節(jié)點的平均故障間隔時間的主效應圖為例,該類參數(shù)的取值范圍為1～5年,因此從1年開始,以0.04年為間隔進行取值。其他參數(shù)類別取值采用第2.2節(jié)中的試驗設計方法設計20組樣本。Vswitch節(jié)點的平均故障間隔時間在每一個取值下,均需要結合表5中的20組樣本進行仿真,得到的可用度均值作為Vswitch節(jié)點的平均故障間隔時間在該取值水平下的可用度值。通過仿真分析,得到部分參數(shù)類別的主效應圖如圖4所示。

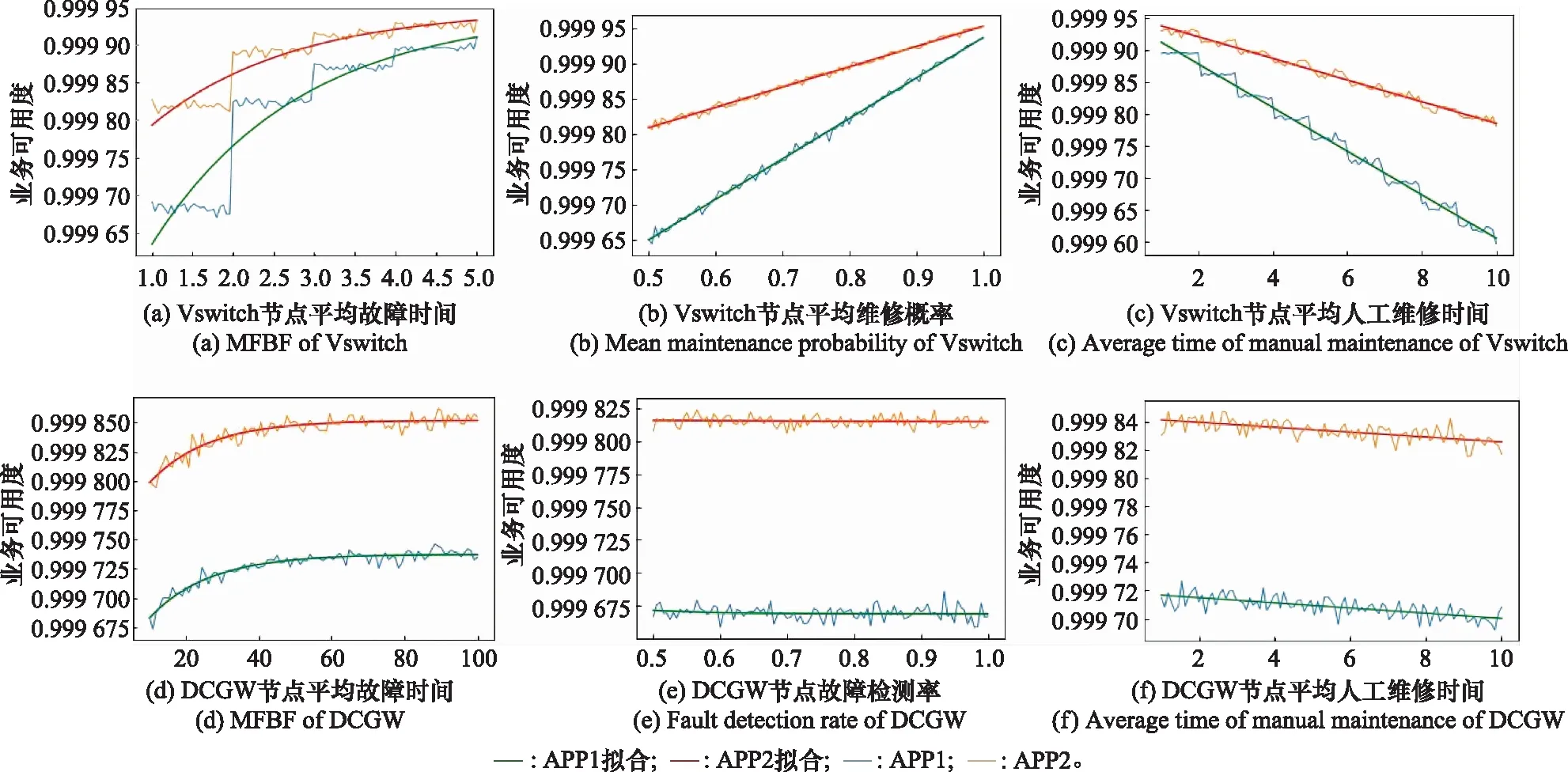
圖4 部分參數(shù)類的主效應圖Fig.4 Main effect diagram of part of the parameter classes

由圖4可知,Vswitch節(jié)點的平均故障間隔時間與業(yè)務可用度呈現(xiàn)出指數(shù)關系,隨著該類參數(shù)值的增加,業(yè)務可用度逐漸收斂于一個固定的值;Vswitch節(jié)點自動維修概率與業(yè)務可用度呈現(xiàn)出線性遞增關系,當該類參數(shù)值增加到最大值1時,業(yè)務可用度也達到最大值;Vswitch節(jié)點平均人工維修時間與業(yè)務可用度呈現(xiàn)出線性遞減關系,當該類參數(shù)值增加到最大值10時,業(yè)務可用度也達到最小值。DCGW節(jié)點平均故障間隔時間與業(yè)務可用度呈現(xiàn)出指數(shù)關系; DCGW節(jié)點故障檢測率、DCGW節(jié)點平均人工維修時間與業(yè)務可用度呈現(xiàn)出線性關系,但是隨著非關鍵參數(shù)類的變化,業(yè)務可用度基本保持不變。

從主效應圖可以看出,分析的關鍵參數(shù)類別與業(yè)務可用度呈單調關系,為了定量衡量不同類別參數(shù)對業(yè)務可用度的影響大小,進一步擬合出整網(wǎng)業(yè)務平均可用度的斜率,將整網(wǎng)業(yè)務平均可用度在參數(shù)取值范圍內(nèi)的平均斜率作為敏感性分析指標,在求平均斜率的過程中,將參數(shù)類的取值進行歸一化處理。通過比較不同參數(shù)類別的平均斜率的絕對值,得到平均斜率排序結果如表10所示,可以找到平均斜率絕對值最大的3個參數(shù)類別為:Vswitch節(jié)點平均故障間隔時間、Vswitch節(jié)點自動維修概率、Vswitch節(jié)點平均人工維修時間。通過主效應圖的平均斜率與全效應指數(shù)的排序對比可知,兩種方法找到的關鍵參數(shù)類別相同。因此，本文找到的關鍵參數(shù)能夠對業(yè)務可用度造成更大的影響,可以驗證本文找到的關鍵參數(shù)類的合理性。

而在本文案例中,由于Vswitch節(jié)點的平均故障間隔時間較小,而且當其發(fā)生故障后業(yè)務無法進行遷移和倒換,只能等待其修復。因此,Vswitch節(jié)點的故障修復參數(shù)會對網(wǎng)絡中的業(yè)務可靠性造成較大的影響,即在不同的NFV中,Vswitch節(jié)點最為關鍵,該類節(jié)點的相關故障修復參數(shù)也更關鍵。Vs1和Vs2上初始部署有業(yè)務,只有當S1或者S2發(fā)生故障時業(yè)務才有可能會遷移到Vs3上。因此,Vs3上承載的業(yè)務少于Vs1和Vs2,Vs1和Vs2的故障參數(shù)會對業(yè)務可用度造成更大的影響。故在該案例中,對業(yè)務可靠性影響最大的關鍵參數(shù)為Vs1設備自動維修概率、Vs1設備平均故障間隔時間、Vs2設備自動維修概率、Vs2設備的平均故障間隔時間,該結果與上述描述并不矛盾,進一步證明了本文找到的關鍵參數(shù)的合理性。通過對案例的分析可以發(fā)現(xiàn),雖然隨著不同案例中業(yè)務部署的不同,網(wǎng)絡中關鍵的具體設備參數(shù)會存在差異,但是關鍵的參數(shù)類別與網(wǎng)絡演化的規(guī)則也密切相關。

表10 主效應圖的平均斜率與全效應指數(shù)的參數(shù)排序對比

對比本文方法與主效應圖方法分別找到的關鍵參數(shù)可以發(fā)現(xiàn),在分析結果上,主效應圖的方法只能對相互獨立的參數(shù)類別(一類設備的參數(shù))進行敏感性分析,而本文方法可以找到相互耦合的參數(shù)(一個設備的參數(shù))中的關鍵參數(shù),而且保證了結果的準確性;在分析效率上,主效應圖需要的仿真樣本數(shù)為20×25×100,而本文方法所需要的仿真樣本數(shù)為20×(25+2+1),遠小于主效應圖的方法。

4 結 論

現(xiàn)有的敏感性分析方法僅能對局部參數(shù)或者構建數(shù)學代理模型對相互獨立的全局參數(shù)進行敏感性分析,而復雜系統(tǒng)模型參數(shù)眾多且參數(shù)之間相互影響耦合,已有的敏感性分析方法無法找到具有參數(shù)耦合特點模型的關鍵參數(shù)。所以,本文提出一種基于網(wǎng)絡演化模型的多類參數(shù)敏感性分析方法,對網(wǎng)絡業(yè)務可靠性的各類影響參數(shù)的敏感性進行分析,找出影響最大、最敏感的主要參數(shù)類別。進一步提出了基于動態(tài)業(yè)務介數(shù)的方法,對不同位置的設備的參數(shù)的敏感性進行解耦,找到關鍵的具體設備參數(shù)。通過對比分析可以發(fā)現(xiàn)主效應圖只能對不同類別的獨立參數(shù)進行排序,找到的關鍵參數(shù)也只是在參數(shù)的局部取值成立,而本文所提方法可以在網(wǎng)絡中所有設備的參數(shù)都相互耦合的情況下對相互耦合(仿真過程中的取值相同)的同一類參數(shù)進行敏感性排序,最終找到整網(wǎng)中所有構件的所有參數(shù)中在全局范圍內(nèi)的關鍵參數(shù),而且所需要的仿真樣本量也遠小于已有的敏感性分析方法。