輪胎破片沖擊機身的非等比例相似模型研究*

康 煌，王 舒，閆文敏，崔海林，郭香華，張慶明

（1. 兵器工業第208 研究所瞬時沖擊國防重點實驗室，北京102202；2. 北京理工大學爆炸科學與技術國家重點實驗室，北京100081）

飛機起降階段，起落架、輪胎等結構承受嚴酷的沖擊載荷作用，其支撐部件將會出現嚴重的變形，甚至可能出現破壞現象。據有關數據統計，飛機輪胎爆炸是最頻發且最危險的事故之一。在極端的壓力載荷作用下充滿高壓氣體的輪胎將產生高速破片，并沖擊機身蒙皮結構，導致內部乘員的生命安全受到威脅。但是，在飛機的結構設計中蒙皮外表面通常不采用任何防護結構。因此，開展機身蒙皮結構抗輪胎破片沖擊性能的實驗研究顯得尤為重要。然而，全尺寸機身結構生產制造成本高昂，在實驗研究中采用縮比模型替代全尺寸機身結構是行之有效的辦法。

許多學者已開展了結構沖擊的相似理論和實驗研究。Mines 等通過實驗手段研究不同沖擊速度、不同沖擊角度下橡膠輪胎破片對鋁合金板的沖擊行為，測試了輪胎橡膠靜態和動態的拉伸、壓縮材料力學性能，實驗結果表明這一沖擊行為并不會引起機身結構的破裂而會產生大變形。Karagiozova 等采用靜、動態的實驗數據校核了橡膠輪胎破片的材料模型，對30°入射角下不同初始速度的橡膠破片沖擊鋁合金板進行了數值模擬，發現所采用的數值模型可以較好地預測全尺寸原型的沖擊實驗結果。Jia 等采用數值模擬技術分析了輪胎破片沖擊機身的前艙壁和主艙段的動態響應，獲取了不同材質機身結構的極限毀傷速度；對比分析發現，復合材料機身的最大接觸壓力約是鋁合金機身的3.3 倍，并且鋁合金前艙壁能夠承受100 m/s 的破片沖擊，而復合材料前艙壁則不能。楊娜娜等基于近場動力學方法分析了破片沖擊作用下艦船復合材料的結構損傷，發現增加少量質量的加筋板的抗沖擊性能優于復合材料層合板，加筋板的筋條尺寸和破片沖擊位置對加筋板的損傷具有明顯的影響。陳映秋等采用相似理論的基本原理，詳細地分析了模型實驗結果預報實船結構應力的可行性，考慮了大尺度縮放的模型與實船的幾何尺度不能用同一比例表達而產生的模型畸變，提出了能夠修正模型畸變的有限元預測系數法，通過該方法實現了模型實驗預測實船的結構應力。秦健等采用π 定律導出了水下爆炸沖擊不同材料加筋板的相似方法，實現了通過普通鋼加筋板模型預報在水下爆炸沖擊作用下船體鋼加筋板原型的動態響應。沈雁鳴等采用量綱分析的方法，推導了超高速撞擊模擬中的相似率表達式，提出了適用于超高速撞擊模擬的相似準則，采用光滑粒子流體動力學數值模擬技術，通過計算厚板開坑、薄板穿透2 種超高速撞擊現象，驗證了相似準則的有效性。楊亞東等開展了鋼筋混凝土結構內爆炸的實驗研究，發現比例模型之間的超壓峰值和壓力波形時程曲線符合相似律，證明了內爆炸特征參量之間存在相似規律。Oshiro 等推導了無量綱相似理論模型，考慮了應變率效應和扭曲幾何引起的不相似行為，通過調整外載荷速度的方式，修正了大尺度縮放模型與原型之間的不相似行為，利用3 種典型的結構沖擊模型驗證了該方法的有效性。在此基礎上，Kong 等開展了半封閉區域爆炸加載柵格板的相似性研究，實現了采用扭曲厚度的相似模型預測原型的動態響應。Kang 等采用量綱分析的方法建立了無量綱相似模型，考慮了應變率效應、表面效應和扭曲幾何對淺埋地雷爆炸沖擊圓板、方板和V 形板相似行為的影響，發現采用修正的非等比例相似模型能夠準確地預測原型的結構響應，可以有效地指導裝甲車抗沖擊性能模型實驗設計。Mazzariol 等探究了動載荷作用下不同材料縮比模型與原型結構之間的相似關系，考慮了尺度效應、材料屬性對相似行為的影響，通過理論分析認為結構材料的密度是影響相似行為的關鍵因素，建立了一個能夠有效預測原型動態響應的相似模型，通過模擬在沖擊載荷作用下梁、板結構的動態力學行為，驗證了該相似方法的準確性。徐坤利用質量、速度及應力將其他力學參量無量綱化，推導了縮比結構的相似方程，采用修正速度的方法，校正了應變率效應引起的縮比結構不相似行為，通過反彈道Taylor 實驗和自由梁橫向撞擊實驗驗證了該方法的有效性。蘇子星等研究了在沖擊載荷作用下材料的應變率效應對相似行為的影響，引入Cowper-Symonds 方程推導了修正外載系數的相似方法，并采用45 鋼和2024 鋁合金驗證了該修正方法的精確性。劉源等基于侵徹阻力模型得到侵徹貫穿混凝土靶板實驗的剛體過載相似準則，提出了非等比例縮比彈體的設計方法，并對縮比模型進行了數值模擬驗證，發現非等比例縮比彈體過載的脈寬、幅值均可實現與原型一致的加載條件。陳材等采用量綱分析的方法分析了圓柱形彈藥空氣中爆炸的相似關系，得到了模型與原型峰值壓力相似的基本條件，通過實驗和數值模擬驗證了縮比模型同彈藥原型的峰值壓力誤差在允許的范圍內，彈藥的縮比模型能夠應用于爆炸損傷實驗。綜上，眾多的學者采用相似理論研究了沖擊載荷作用下結構沖擊模型的縮比規律，但并未針對輪胎破片沖擊機身結構的相似規律進行深入研究。因此，開展橡膠輪胎破片沖擊機身結構的相似模型研究是有必要的，并且具有可行性，能夠節約實驗成本，降低不必要的資源耗費，對指導工程設計具有重要的實際意義。

本文中，采用數值模擬的手段優化機身材料及結構尺寸，分析橡膠輪胎破片的沖擊角度和著靶姿態對機身抗沖擊性能的影響，選擇最優的機身結構和最嚴苛的沖擊角度作為相似原型。采用量綱分析的方法，并基于線性應變率函數，建立無量綱相似關系，通過改變模型破片的加載速度，修正應變率效應和扭曲幾何造成的非等比例機身模型與機身原型的不相似行為，結合數值模擬的方法驗證縮比模型設計方法的合理性。

1 機身結構優化設計

1.1 材料屬性

1.1.1 機身的材料參數

對機身的金屬材料采用Johnson-Cook (J-C)模型，將應力、應變率和溫度等影響因素表示為乘積關系，通過對材料參數的合理取值，能較好地描述金屬材料的動態力學行為，相關表達式為：

本文中對鋁合金和鈦合金均采用J-C 材料模型，選用文獻[3-4]中已測定的材料力學性能參數，見表1，表中ρ 為材料初始密度，為彈性模量，為泊松比。

表1 機身材料參數[3-4]Table 1 Material parameters of fuselage[3-4]

1.1.2 輪胎的材料參數

對輪胎破片采用超彈性體本構模型，該模型基于連續介質力學的唯象理論模型，以材料的宏觀測試特性為依據，建立可以描述變形性質的數學關系：

1.2 有限元模型的檢驗

本文中，建立了長×寬×厚為60 mm×30 mm×15 mm 的輪胎破片有限元模型和長×寬×厚為300 mm×300 mm×1.6 mm 的鋁合金靶板有限元模型，有限元模型中靶板的固定方式與實驗中的保持一致，用螺栓將方形剛性框架固定在鋁合金靶板的四周，其實際受載面的長×寬×厚為260 mm×260 mm×1.6 mm；通過LS-DYNA 動力學模擬軟件，對初始沖擊速度為135 m/s 的輪胎破片分別以30°和80°的角度沖擊鋁合金板的工況進行了數值模擬。

通過對比實驗數據，具體為：靶板中心的最終撓度、應變時間歷程曲線、變形輪廓和橡膠破片的撞擊變形形態等，從而校驗了數值模型的有效性。圖1 中對比了30°沖擊角度β 下不同時刻橡膠輪胎破片變形形貌的高速攝影和本文的數值計算結果，圖中沖擊角度β 為速度矢量與靶板的夾角。從圖1 可以看出，橡膠作為軟體侵徹物在沖擊過程中出現明顯的壓彎和翻滾現象，從沖擊點開始一直貼附于靶板運動，直到彈飛出靶板的邊緣，這表明有限元模型可以較好地模擬橡膠的沖擊運動過程，與實驗觀測到的結果相吻合。

圖1 高速攝影[2]和數值計算分別得到的橡膠輪胎破片以30°沖擊角度和135 m/s 的沖擊速度撞擊鋁合金靶板后不同時刻的變形形貌Fig. 1 Deformation morphologies of the rubber tire fragment with the initial impact velocity of 135 m/s at the impact angle of 30°after its impacting on an aluminum alloy target at different times obtained by high-speed photography[2] and simulation

圖2 中對比了實驗和本文模擬的在輪胎破片以30°和80°的角度沖擊下鋁合金靶板的空間變形輪廓，圖3 中對比了實驗和本文模擬的在輪胎破片以30°的角度沖擊下鋁合金靶板中心點的應變時間歷程曲線。可以看出，數值模擬得到的受沖擊靶板變形輪廓基本與實驗結果相同，中心監測點的應變時間歷程曲線和實驗結果基本一致。

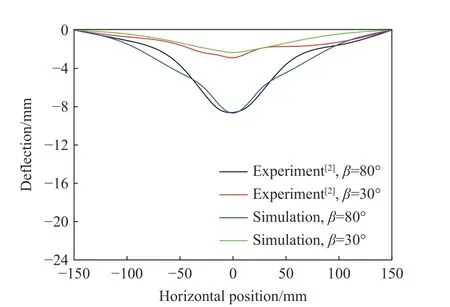
圖2 不同沖擊角度下靶板的空間變形輪廓Fig. 2 Spatial deformation profiles of target plates at different impact angles

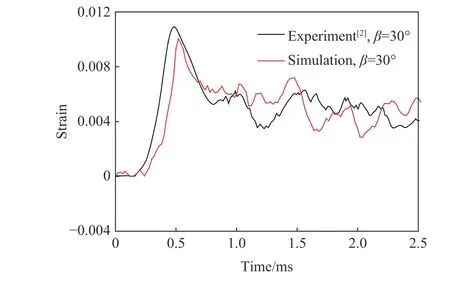
圖3 中心監測點的應變時間歷程曲線Fig. 3 Time history of strain at the central point

表2 對比了靶板中心點的最終撓度的實驗結果和模擬結果，2 個不同角度沖擊作用下的靶板分別表現出彈性和塑性主導的變形行為，模擬值與實驗值的相對偏差分別為18.6%和17.4%。這也進一步說明，本文中建立的有限元模型能夠有效地模擬橡膠沖擊金屬靶板的物理過程。

表2 靶板中心點最終撓度的實驗結果[2]與模擬結果的對比Table 2 Comparison of the residual deformations at the centers of the target plates between experiment[2] and simulation

1.3 破片偏航姿態的影響

為了研究破片偏航姿態對靶板沖擊響應的影響，即破片的沖擊角度和著靶角度的共同作用，著靶角度為輪胎破片中心軸線與靶板的夾角 θ 。當 θ ≤90， β=θ ；當 9 0＜θ＜180， β =θ-90，圖4 為破片以不同姿態沖擊靶板的空間位置示意圖。因此，設置沖擊角度 β 分別為30°、60°和90°；破片的著靶角度θ 為30°、120°，60°、150°、90°和180°，沖擊角度和著靶角度兩兩相互對應。采用數值軟件LS-DYNA 模擬分析相同沖擊速度下不同著靶角度對靶板沖擊響應的影響，具體模擬參數及結果如表3 所示。

圖4 不同姿態的破片沖擊靶板的空間位置Fig. 4 Spatial positions of the fragments with different attitudes impacting into target plates

表3 不同沖擊條件下方形鋁靶板中心的響應參數Table 3 Response parameters at the centers of square aluminum plates under different impact conditions

表3 展示了不同沖擊條件下方形鋁靶板中心的響應參數，包括中心瞬時最大撓度、中心最終撓度和脈寬，脈寬為撓曲線的第1 個波谷到第1 個波峰所對應的2 個時刻的時間差。圖5 為不同著靶角度下靶板的最終變形輪廓曲線，圖6 為不同著靶角度下靶板中心點的撓度時間歷程曲線。由表3 和圖5～6 可知：靶板中心撓度（代指瞬時最大撓度和最終撓度）的幅值大小主要取決于沖擊角度，而破片的偏航姿態（著靶角度）對靶板中心撓度幅值的影響次之；靶板撓曲線的脈寬隨著靶角度的增大而增大；在相同沖擊角度的情況下，鈍角著靶比銳角著靶對靶板造成的沖擊作用更嚴重，表現為鈍角著靶下靶板中心撓度更大；然而，在30°沖擊角度下，靶板中心撓度隨著靶姿態的變化出現異常現象，即120°著靶下靶板中心的瞬時最大撓度比30°著靶下的小，而靶板中心的最終撓度更大。對于著靶角為銳角的情況，靶板的最終變形輪廓明顯不對稱。

圖5 靶板的最終變形輪廓曲線Fig. 5 Residual deformation profiles of target plates

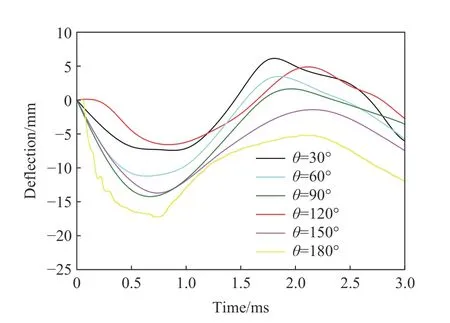
圖6 靶板中心撓度的時間歷程曲線Fig. 6 Deflection time history at the center points of target plates

針對上述發現的現象及規律，分析認為：沖擊角度決定了靶板豎直方向（向）所受的沖擊速度分量，著靶角度決定了靶板中心區域的瞬時受載面積，以及破片初次沖擊靶板后的運動行為，即銳角著靶姿態出現反向回彈，鈍角著靶姿態出現沿靶板的橫向移動，并可能發生二次碰撞。對于銳角著靶姿態下靶板輪廓的不對稱現象，是由于銳角著靶所產生的橫向沖擊速度分量和較小的瞬時受載面積，二者共同作用造成了靶板變形輪廓的不對稱。對于30°沖擊角度下靶板撓度的異常現象，是由于靶板中心的瞬時最大撓度強烈依賴于靶板變形的局部化程度，而最終撓度取決于靶板的受載面積、塑性變形程度和回彈響應；這就解釋了表3 中30°沖擊角度的2 種不同著靶姿態下出現的異常現象，即在相同的瞬時沖擊速度下，銳角著靶的局部化現象導致靶板中心的瞬時撓度更大，而局部化區域以外并未產生足夠的塑性變形，因此銳角著靶姿態下靶板的回彈變形幅值更大（回彈量=瞬時最大變形-最終變形），而靶板中心的最終撓度更小。

1.4 機身材料及厚度的影響

機身結構設計需要考慮整機質量以及耐熱、強度等因素，通常情況下，機身不會配備質量過大的裝甲防護結構，這就限制了機身的抗沖擊性能。在輕量化的要求下，機身抵御外來破片沖擊的能力仍需提升。建立真實的機身結構抗輪胎破片垂直侵徹的有限元模型，如圖7 所示。模型幾何尺寸參數為：機身直徑，3 856 mm；寬度，1 200 mm；內部加筋間距，500 mm；主肋骨間距，600 mm；輪胎破片尺寸，400 mm×100 mm×28 mm。

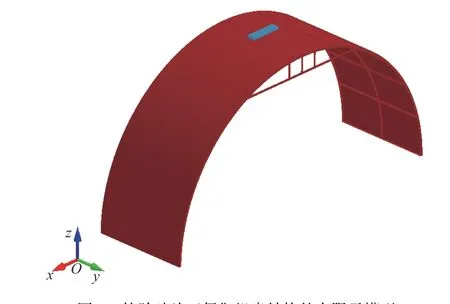
圖7 輪胎破片正侵徹機身結構的有限元模型Fig. 7 The finite element model for a tire fragment impacting the fuselage

機身結構相對復雜造成數值模擬的結構響應時間過長，而機身結構產生的最大瞬時變形撓度是造成乘員及結構損傷的重要因素，因此將其作為抗沖擊性能的衡量指標，將靶板的最大瞬時撓度簡稱為靶板撓度。選用鋁合金和鈦合金2 種材料，常用的機身厚度為3～6 mm，鋁合金靶板厚度設置為4.0、5.0 和6.0 mm，鈦合金靶板厚度設置為3.0、3.5 和4.0 mm。選用最嚴苛的沖擊條件，破片沖擊速度為150 m/s，著靶角度為180°，沖擊角度為90°。機身幾何結構及響應參數如表4 所示，機身中心點的瞬時最大撓度的時間歷程曲線如圖8 所示。

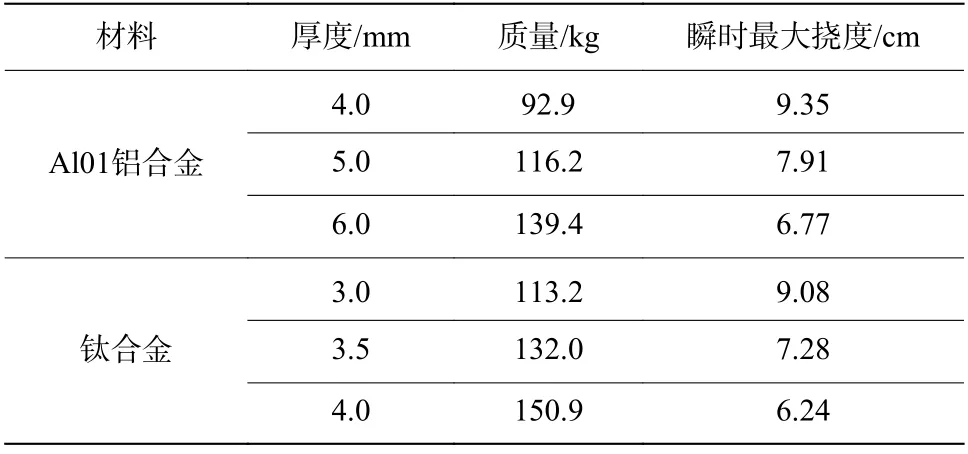
表4 機身的幾何結構及響應參數Table 4 Geometric structure and response parameters of the fuselage

表4 和圖8 對比了不同材料和結構厚度對靶板沖擊響應的影響，可以看出：3.5 mm 厚鈦合金靶板、4.0 mm 厚鈦合金靶板和6.0 mm 厚鋁合金靶板三者中心的瞬時最大撓度較小，分別為7.28、6.24 和6.77 cm；而三者的質量由大到小依次是4.0 mm 厚鈦合金靶板的質量最大，6.0 mm厚鋁合金靶板的質量次之，3.5mm 鈦合金靶板的質量最小，三者占用的空間體積由大到小依次是6.0 mm 厚鋁合金靶板占用的空間體積最大，4.0 mm厚鈦合金靶板占用的空間體積次之，3.5 mm 厚鈦合金靶板占用的空間體積最小；6.0 mm 厚鋁合金靶板的變形撓度最小，但其厚度過大造成其空間占用體積幾乎是3.5 mm 厚鈦合金靶板的2 倍；同樣，3.5 mm 厚鈦合金靶板的質量比4.0 mm 厚鈦合金靶板的小18.9 kg，盡管后者中心的瞬時最大撓度要小1.04 cm。在輕量化要求的前提條件，3.5 mm 厚鈦合金結構兼顧空間占用體積小、輕量化和抗沖擊性能好等多種因素，是機身結構和材料的最佳選擇之一。

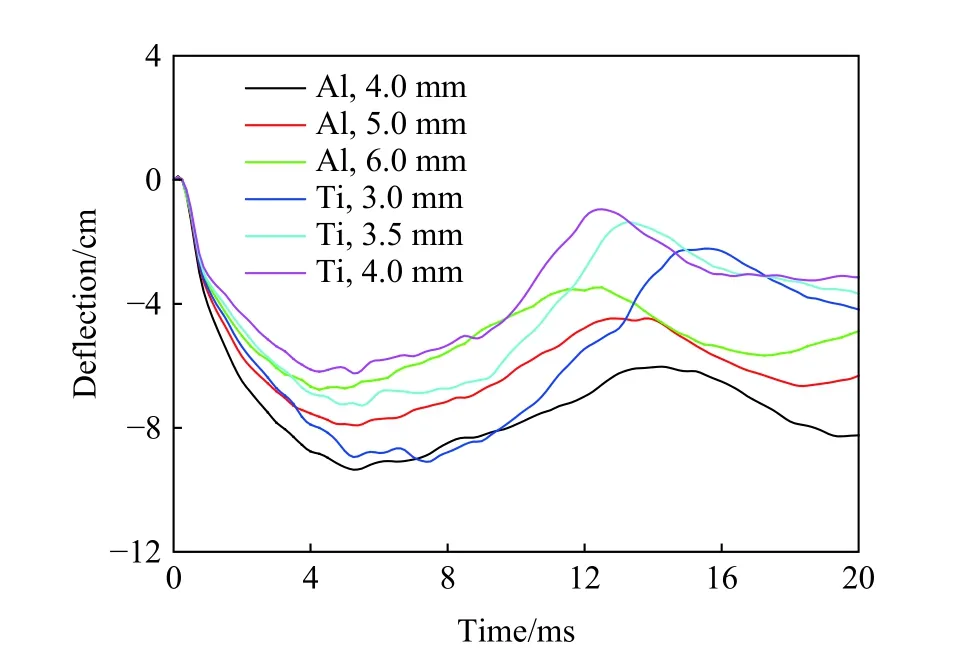
圖8 機身中心點的瞬時最大撓度的時間歷程曲線Fig. 8 Time histories of the maximum instantaneous deflections at the centers of the fuselages

圖9 對比了靶板中心的瞬時最大撓度時刻機身結構的等效應力和有效塑性應變云圖，可以看出，鈦合金靶板中心區域產生的平均應力約為540 MPa，約為鋁合金靶板中心區域平均應力的2 倍，并且鈦合金靶板的應力分布區域更廣。鋁合金靶板中心區域的平均塑性應變約為0.035，約為鈦合金靶板中心區域平均塑性應變的2 倍，鋁合金靶板的有效塑性應變分布區域更大。這表明，兩者抵抗輪胎破片沖擊的機制不同，鈦合金靶板形成全局的沖擊應力，而鋁合金靶板以局部變形吸能的方式耗散沖擊動能。

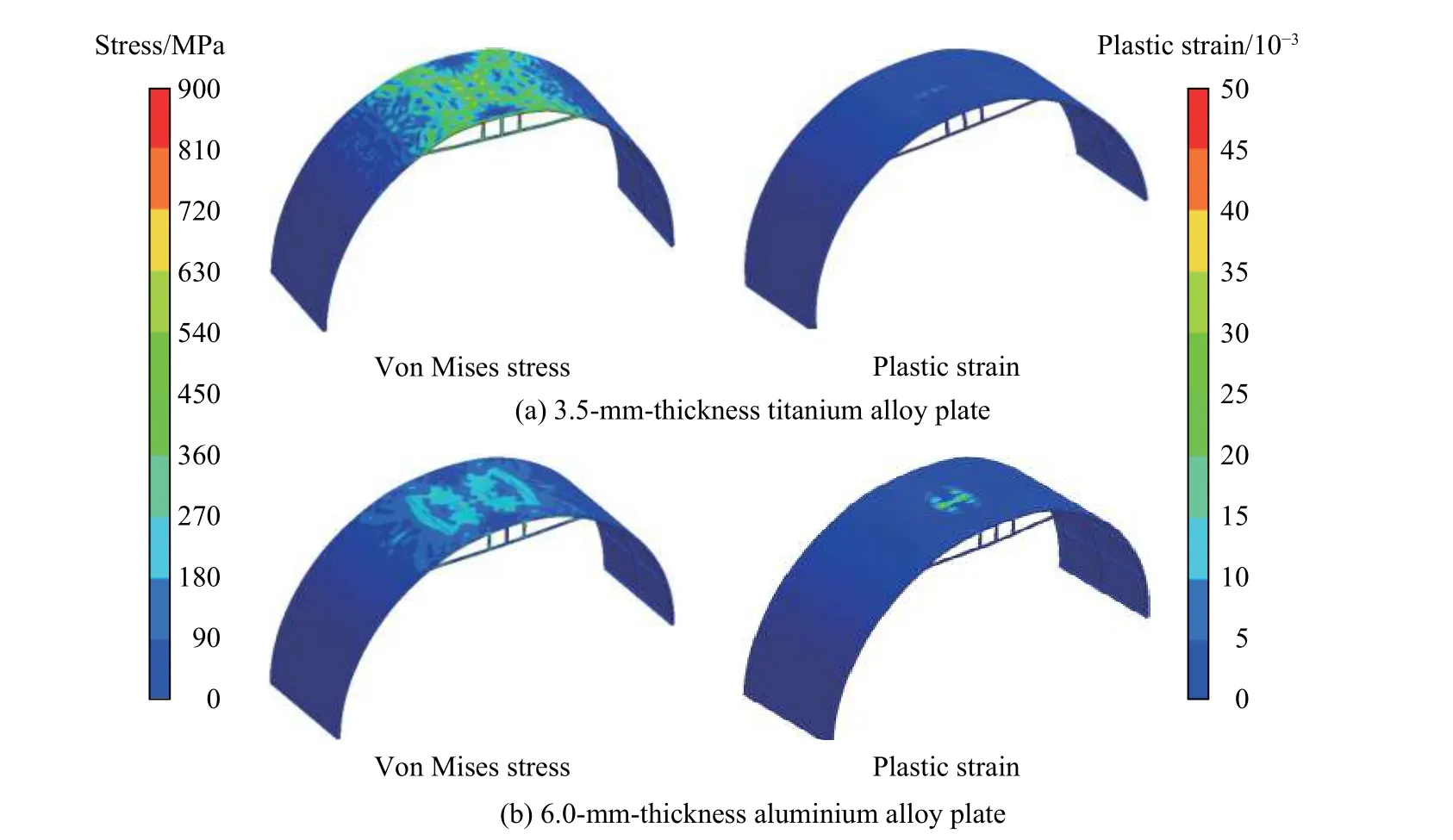
圖9 瞬時最大撓度時刻靶板中心的等效應力和有效塑性應變云圖Fig. 9 Equivalent stress and plastic strain of the fuselage structures at the instant of the maximum transient deformation

2 無量綱修正關系

金屬結構受到強沖擊載荷作用會產生明顯的應變率效應，而大尺度縮比后應變率效應是導致幾何不相似的關鍵因素，許多研究結論證實了這一觀點。因此，Oshiro 等開展了結構沖擊的相似研究，嚴格地證明了應變率效應的影響，并提出了合理的修正方法。在此基礎上，本文中采用該修正方法分析應變率效應對輪胎橡膠破片沖擊機身結構的相似行為的影響，并考慮大尺度縮放扭曲厚度模型的相似行為，建立相應的修正關系，實現扭曲厚度的非等比例模型預測原型響應。

2.1 應變率效應的修正關系

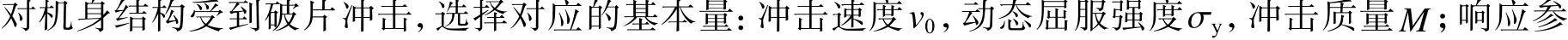
2.2 扭曲厚度的修正關系

薄壁結構的大尺度縮放會導致其厚度方向的尺寸過小，引起材料的剛度和強度變化，無法制造出符合材料性能要求的靶板。因此，提出扭曲厚度的縮放模型，以便滿足實際材料狀態的需求。厚度的變化必然會加劇相似模型的失真程度，為解決厚度畸變導致的不相似行為，提出扭曲比例系數 α來表征相似模型厚度方向上的單獨變化，表示扭曲模型厚度的幾何尺寸。扭曲厚度模型與等比例相似模型的幾何比例因子：

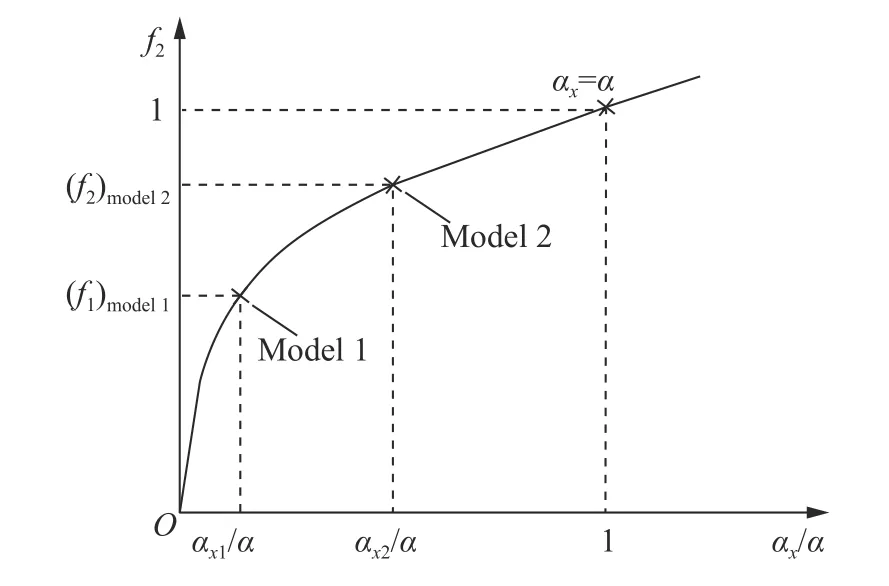
圖10 扭曲厚度模型的修正函數 f2 與厚度變化因子 α x/α 的理想關系曲線[10]Fig. 10 The ideal curve of function f2 and the thickness factor α x/α [10]

3 驗證相似模型

本文中提出一種能夠快速獲取工程縮比模型的方法。采用有限元軟件LS-DYNA，分析應變率效應和扭曲厚度對相似行為的影響，并通過數值模擬驗證了縮比模型與機身結構原型的相似性，提出了快速獲取縮比模型實驗的設計方法。工程設計過程中，首先，對比選擇最嚴酷的沖擊條件；然后，以此為基礎綜合分析多種限制因素并優選出最佳的結構模型。接著，選用最佳的結構和最嚴酷的沖擊條件作為原型工況，設計等比例模型和幾何尺寸扭曲的非等比例模型，采用相似修正方程獲取對應的修正參數。最后，基于數值模擬驗證修正參數的精確性，設計修正后的模型作為實驗用的縮比模型，相似模型設計流程如圖11 所示。

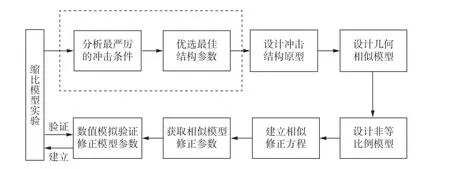
圖11 相似模型設計流程Fig. 11 Design process for the scaled-down model

3.1 應變率效應的影響

在第2 節的基礎上，選用輪胎破片對原型機身沖擊實驗的具體參數為：橡膠輪胎破片沖擊速度150 m/s 條件下，沖擊角度90°、著靶角度為180°沖擊3.5 mm 厚鈦合金靶板結構。機身機構原型與等比例模型的比例因子分別為1、1/10、1/8、1/5 和1/2；采用數值軟件LS-DYNA 模擬150 m/s 輪胎破片沖擊未修正的等比例縮放模型，獲1 取相應模型機身結構中心的應變率分別為392、3 856、3 185、1 963 和794 s，代入式(3)便可獲取相應的修正速度，如表5 所示。

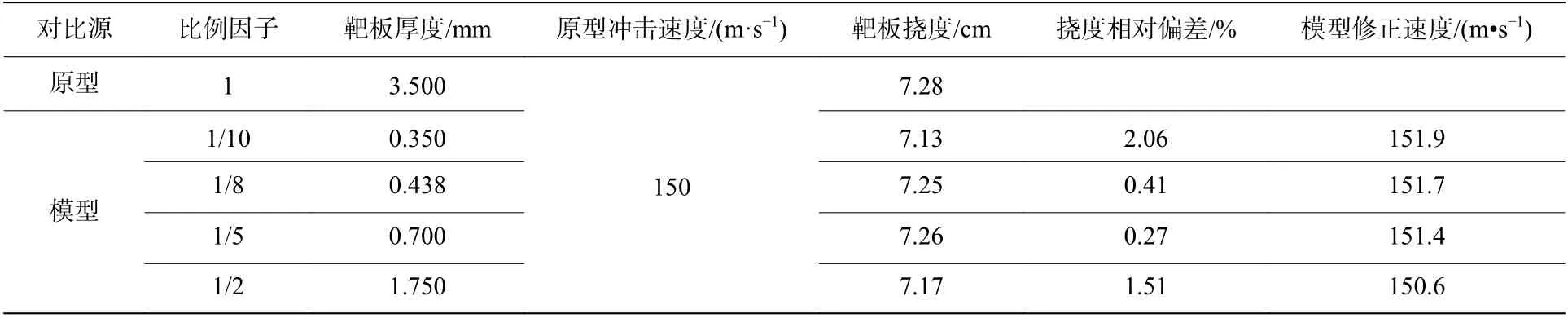
表5 對比模型與原型的瞬時最大撓度Table 5 Comparison of the maximum displacement between the model and the prototype

其中，應變率近似定義為受沖擊靶板中心位置處有效塑性應變隨時間的變化率，通過模擬數值模型中的監測點獲取靶板中心位置處的應變-時間曲線，并通過公式計算獲取相應的應變率，即 ε ˙=(ε-ε)/(-) 。未修正的完全相似模型的中心變形時間歷程曲線如圖12所示。

由圖12 和表5 可以看出，未修正的完全相似模型與原型結果的偏差較小，可以較好地預測原型的結構變形。這說明應變率效應對150 m/s輪胎破片沖擊機身結構的相似行為幾乎沒有影響，未修正的幾何完全相似模型就可以用于預測原型結構的動態響應。

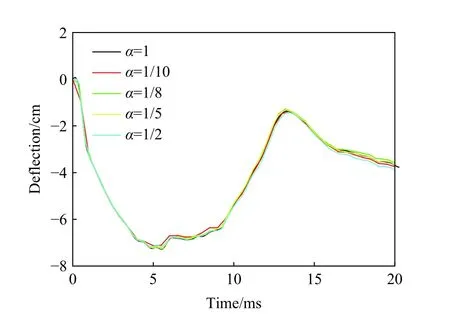
圖12 對比未修正的等比例模型和原型的中心變形的時間歷程曲線Fig. 12 Comparison of deformation-time curves between the uncorrected scaled models and the prototype

3.2 扭曲厚度的影響

在3.1 節中，大尺度縮放模型的靶板厚度分別為0.350、0.438 和0.700 mm。由于制造技術的限制，難以生產出符合材料強度要求的大尺度縮放模型實物。因此，引入扭曲厚度的非等比例模型處理這一問題，仍將考慮應變率效應微小變化對非等比例修正模型的影響。在本節中，采用等比例縮放模型的比例因子 α =1/8，模型的機身結構厚度=0.438 mm。

基于2.2 節中提出的扭曲模型的修正方法，為獲取修正函數的指數，設定2 個不同的扭曲模型系數α=2.0 和α=3.5 ，對應的機身厚度為0.87 和1.52 mm。設定4 組不同的指數，分別為1.00、1.05、1.12、1.15，通過數字計算獲取2 個扭曲模型靶板的變形撓度 δ ；當 δ≈δ，便可獲取對應的扭曲函數的指數，不同指數對應的沖擊速度和撓度如表6 所示。最后，將求解得到的指數代入=(α/α)，便可計算扭曲厚度非等比例模型的修正速度。

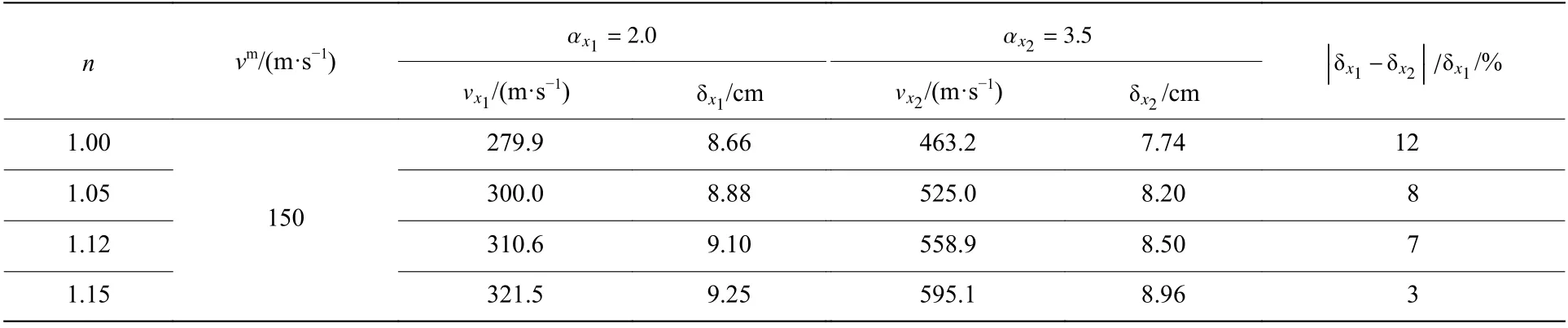
表6 不同指數對應的沖擊速度和撓度Table 6 Impact velocities and central deflections in relation to different exponents

由表6 可以看出，隨著指數的增大，2 個扭曲模型撓度的相對偏差減小；當=1.15 時，2 個扭曲模型撓度的偏差僅為3%；當＞1.15 時，存在某一極值點使兩者的撓度偏差接近零；而進一步增大指數，兩者的撓度偏差會逐漸增大，這是由修正函數的性質所決定的。由模擬結果發現，當＞1.15 時，機身結構會出現明顯的破壞，3%的撓度相對偏差足以保證非等比例相似模型的修正精度。因此，當=1.15 時，獲得扭曲厚度模型的修正方程為：

為了驗證扭曲厚度模型的有效性，假定扭曲因子分別為2.29、2.74 和3.43，將求解的參數和分別代入式(3)和(8)，計算獲得扭曲厚度模型的修正速度，將參數代入數值模擬軟件DYNA 獲取未修正模型和修正結果。表7 對比原型與模型的靶板瞬時最大撓度，可以看出，修正方程能夠解決扭曲厚度所導致的偏差，修正后的3 個不同厚度的扭曲模型的預測值最大偏差不超過5.1%。

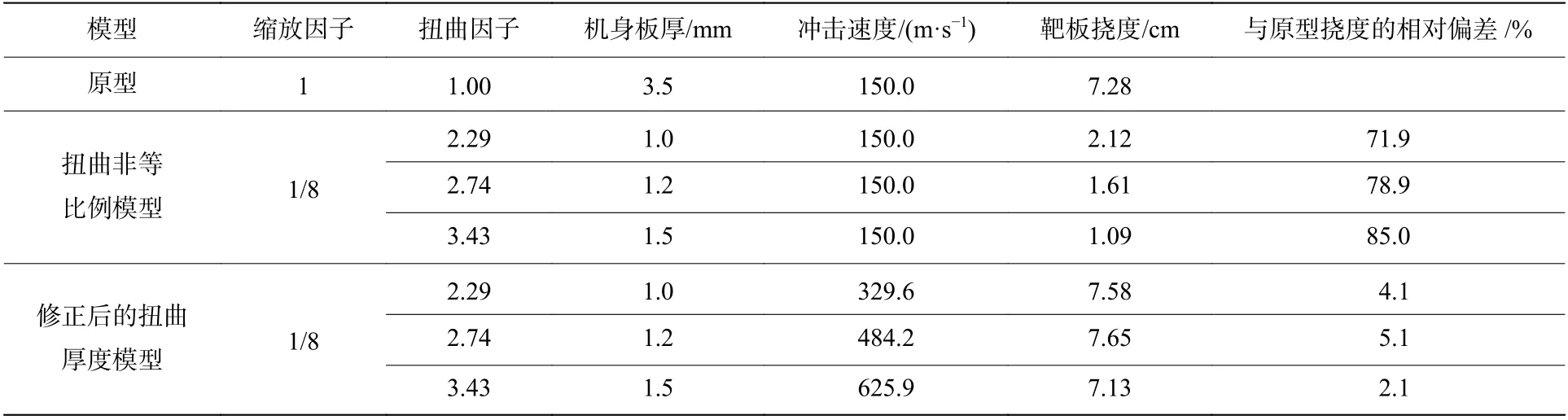
表7 對比原型與模型的靶板瞬時最大撓度Table 7 Comparison of the maximum deflection between the prototype and models

圖13 對比了扭曲厚度的非等比例模型與原型的撓度時間歷程曲線，可以看出，修正方法可以彌補因板厚扭曲而導致的撓度峰值和靶板響應模型不一致的問題。然而，在時間域上，3 個修正的扭曲厚度模型的撓曲線的分布與原型的相差較大。對比發現，原型撓度曲線的第1 個脈寬遠大于其他修正模型的，未修正扭曲模型的撓度曲線的脈寬具有較好的一致性；此外，隨著扭曲板厚的增大，修正模型的撓度脈寬逐漸減小。分析發現，在時間域上，扭曲模型產生的行為不一致現象，是由橡膠破片的材料性質所決定的；這是因為該修正方法通過調整載荷速度從而實現扭曲厚度模型行為的相似性，而橡膠破片沖擊靶板會出現明顯的“彈飛”現象，導致修正速度越高的扭曲模型，橡膠破片沖擊作用靶板的時間越短。因此，橡膠的材料屬性是引起修正扭曲模型響應曲線出現不相似行為的關鍵因素。

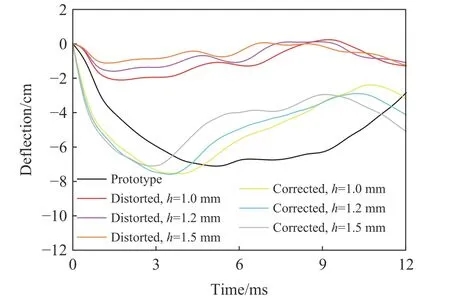
圖13 對比非等比例模型與原型的撓度時間歷程曲線Fig. 13 Comparison of deformation-time curves for the center points of the plates

圖14 對比了非等比例模型與原型靶板的最大變形時刻的輪廓圖。可以看出，不同扭曲厚度模型的靶板撓度輪廓變形與原型結果基本一致。在空間域上，靶板的撓度與原型的變形曲線基本一致。因此，采用該修正方法仍然能夠準確地預測原型板的最大撓度，能夠有效地指導工程設計。

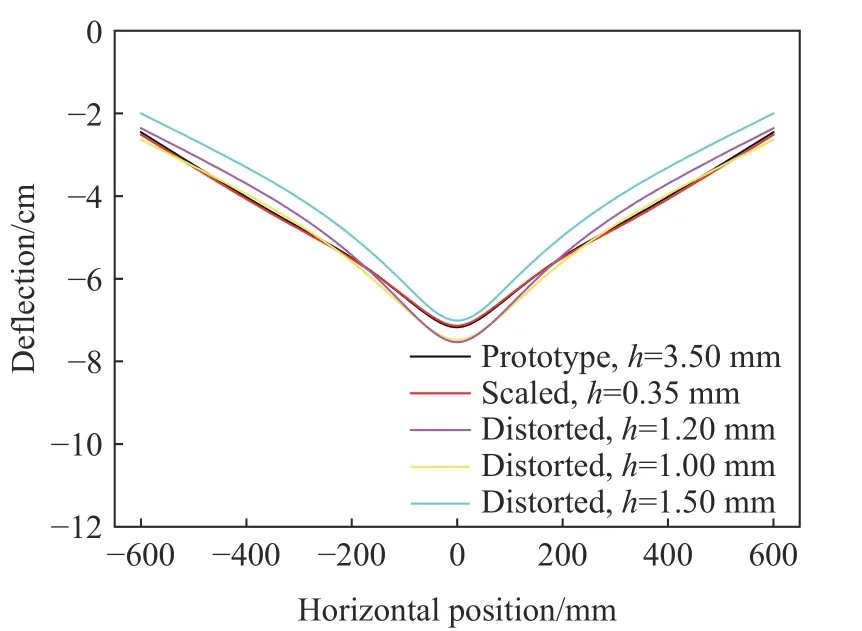
圖14 非等比例模型與原型靶板的最大變形時刻的輪廓圖Fig. 14 The maximum deformation profiles of the plates for the incomplete scaling model and prototype

4 結 束 語

飛機起降階段產生的不可控因素會使起落架和輪胎承受巨大的壓力，導致飛機輪胎發生爆炸，產生四散的破片沖擊飛機四周及威脅艙內乘員的安全。因此，為了解決全尺寸原型抗沖擊性能實驗耗費巨大的問題，開展輪胎破片沖擊機身結構的相似性研究，建立相似模型設計方法，以便實現快速獲取相似模型的設計方案。

(1)基于測試實驗數據，驗證了橡膠輪胎破片沖擊鋁合金靶板有限元模型的有效性。為建立受沖擊機身的原型，綜合分析了多種因素，結果表明：150 m/s 輪胎破片沖擊速度下，90°沖擊角度和180°著靶角度為輪胎破片最嚴苛的沖擊條件；3.5 mm 厚鈦合金板是機身的最佳選擇。

(2)在沖擊角度為30°的情況下，銳角著靶比鈍角著靶的受沖擊靶板的瞬時最大撓度更大，而最終撓度更小。因為沖擊角度較小導致受載靶板的局部化塑性變形程度更高，所以銳角著靶的瞬時最大撓度更大；然而，局部化區域以外受彈性變形主導，導致靶板的回彈幅值更大，所以最終撓度更小。

(3)基于量綱分析方法，建立了應變率效應和扭曲幾何的無量綱修正公式。為驗證該相似方法，建立了不同縮放系數的等比例和非等比例相似模型。未修正模型的結果表明，破片沖擊機身結構的應變率效應不會影響等比例縮放模型的相似性，而扭曲厚度會導致非等比例縮放模型產生嚴重的不相似行為。修正模型的結果表明：在時間域上，修正模型的撓度曲線的脈寬明顯小于原型的，這是由橡膠材料的特殊性質所決定的；然而，在空間域上，修正模型的變形輪廓曲線和瞬時最大撓度的最大偏差不超過5.1%。這表明采用本文中所提出的修正方法，可以快速建立輪胎破片沖擊機身結構的非等比例相似模型，實現準確預測原型機身結構的沖擊響應。