新型恒力機構的設計與分析
單燁,鐘建華,丁冰曉
(1.福州大學 先進制造學院,福建 泉州 362200;2.福州大學 機械工程及自動化學院,福建 福州 350116;3.吉首大學 物理與機電工程學院,湖南 吉首 416000)
恒力機構在一定的輸入位移范圍內能夠輸出恒定或者接近恒定的力,在精密儀器[1]、振動隔離[2]、過載保護、微機電系統等方面應用廣泛。柔順機構是一種利用柔性構件的彈性變形來實現運動、能量、力的傳遞和轉化的機構[3]。柔順恒力機構是一種被動的力控方式,因此不需要精密的傳感器和復雜的控制算法[4],降低了力控的成本和開發的難度。與傳統的恒力機構相比,柔順恒力機構不僅具有無摩擦,無磨損,無需潤滑等特點[5],還具有與位置環境靈活交互的特點。
很多學者對柔順恒力機構進行了深入研究,如Ma等[6]利用柔順梁的第二彎曲模式開發出了大行程的常力機構,固定導向柔性梁的雙梁約束模型(Bi-BCM)表明,當固定導向梁偏轉到其第二彎曲模式(即偏轉的梁帶有兩個拐點)時,其頂端軸力保持不變;Hao等[7]利用正剛度機構和負剛度機構并聯構成了準零剛度機構即恒力機構并分析了影響恒力機構特性的參數,同時利用兩個對稱的恒力機構設計了一種恒力夾具,通過調節在正剛度機構上施加的力,可以調節恒力機構恒力的大小。針對空間恒力機構,Zhou等[8]通過將新型負剛度機構與正剛度機構并聯連接,開發了一種具有良好軸向導向能力的準零剛度抗干擾機構,該機構呈現出空間對稱性,使得機構具有較大的平面內橫向剛度。本文提出一種新型恒力機構,并對機構進行數學建模和有限元分析。
1 恒力機構的設計
常見的恒力機構是由具有正剛度特性的正剛度機構和具有負剛度特性的負剛度機構并聯而成[9]。正剛度機構符合胡克定律,其彈性力與位移成正比;負剛度機構一般為具有雙穩態特性的雙穩態梁。并聯型恒力機構設計原理[10]如圖1所示。
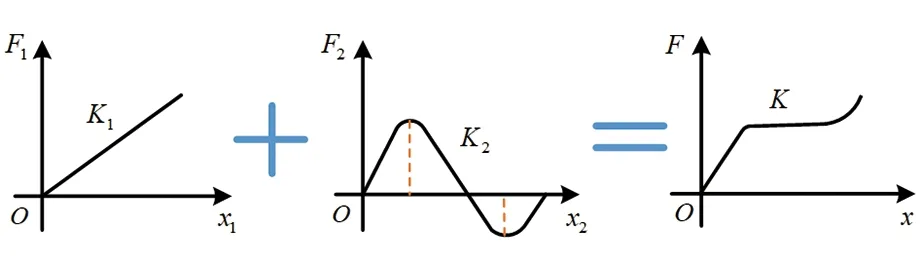
圖1 并聯型恒力機構原理Fig.1 Principle of parallel constant force mechanism
根據圖1可得:
(1)
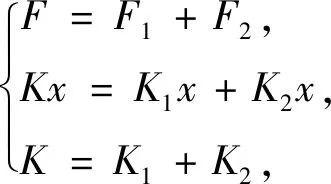
(2)
式中:F1為正剛度機構的彈力;F2為雙穩態機構在負剛度特性階段的彈力;F為恒力機構的彈力;K1為正剛度機構的剛度;K2為負剛度機構在負剛度特性階段的剛度;K為恒力機構剛度;x為機構的輸入位移。
當K1和K2大小相同時,相互抵消,機構表現出零剛度特性,實現常力輸出[11]。因此
(3)
式中:Δx為恒力機構的位移;Δx1為正剛度機構的位移;Δx2為負剛度機構的位移。
(4)
式中K為恒力機構的剛度。
根據上述原理,構建出如圖2所示的恒力機構[12],該機構由雙穩態梁和折疊直梁組成的正剛度機構并聯而成[13]。
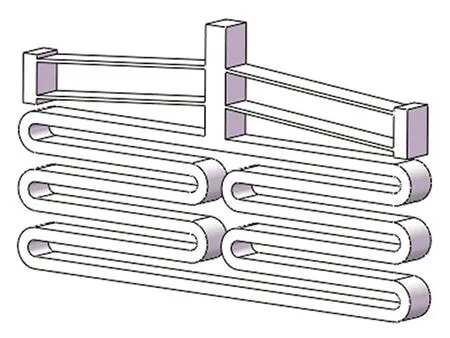
圖2 恒力機構模型圖Fig.2 Model drawing of constant force mechanism
正剛度機構基于柔性的線性彈簧原理實現,設計結構如圖3所示。正剛度線性彈簧機構是一種對稱折疊的設計,能使機構在平面內進行較大的平移運動,且易于制造[14]。折疊設計消除了正剛度機構軸向位移的負面影響,使載荷在主平移方向上加強。
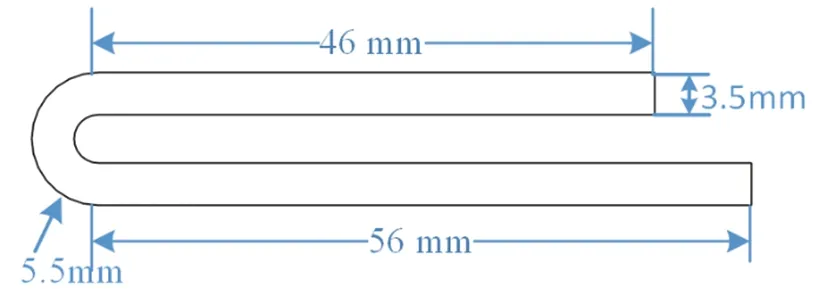
圖3 正剛度機構參數Fig.3 Parameters of positive stiffness mechanism
1.1 負剛度機構
本文提出的負剛度機構由一對空間對稱傾斜直梁組成,如圖4所示。雙穩態梁的尺寸參數見表1。
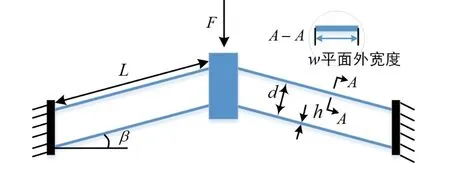
圖4 雙穩態梁機構Fig.4 Bistable beam mechanism

表1 雙穩態機構參數Tab.1 Bistable mechanism parameters
雙穩態梁在機構的變形過程中有兩個穩定的狀態,當處于這兩個穩定的狀態時,機構并不需要外力便可維持自身的狀態[15]。
雙穩態梁是由兩對固定傾斜梁對稱分布而成,由于結構的對稱分布,使雙穩態梁具有負剛度特性。如圖5所示,D0-D1和D3-D4階段為正剛度階段[16],D1-D3為負剛度階段,其中D1-D2與D2-D3階段機構彈力的方向相反[17]。
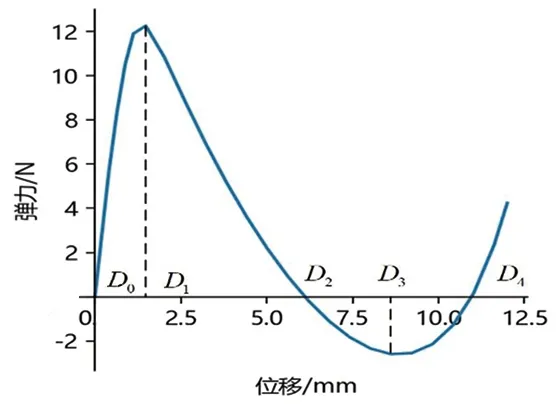
圖5 雙穩態梁特性圖Fig.5 Bistable beam characteristic diagram
1.2 雙穩態梁的結構分析
對于柔順梁的大變形問題,可以把懸臂梁看做歐拉-伯努利梁來處理,符合平截面假定和垂直法線假定,只考慮彎曲變形,忽略梁的剪切變形。Euler-Bernoulli梁方程為[18]
(5)
懸臂梁的模型分析如圖6所示,初始形狀是直的懸臂梁受到力ηP和M0的組合作用,其中ηP可以分解為水平方向的nP和豎直方向的P。懸臂梁變形過后自由端的坐標值為(a,b),自由端的變形角為θ0[19],取懸臂梁上任意一點坐標為(x,y),則該點處力矩可以表示為
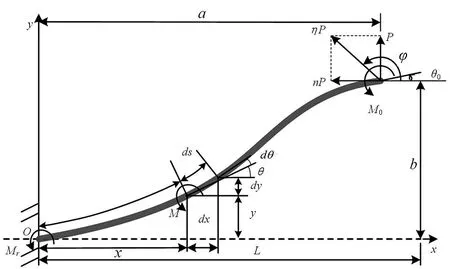
圖6 懸臂梁的模型分析Fig.6 Model analysis of cantilever beam
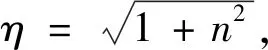
(6)
M=P(a-x)+nP(b-y)+M0。
(7)
將式(5)、式(7)代入可得
(8)
式中:E為懸臂梁的楊氏模量;I為慣性矩;式(8)又可以寫成
(9)
式中θ0是懸臂梁末端彎曲的角度。由式(9)可得

(10)
式中:a/L和b/L分別是懸臂梁變形后在x軸和y軸上的無量綱坐標。根據彈性理論,彎曲梁中可以有任意個拐點[20-21],令拐點的數量為m,如圖7所示。
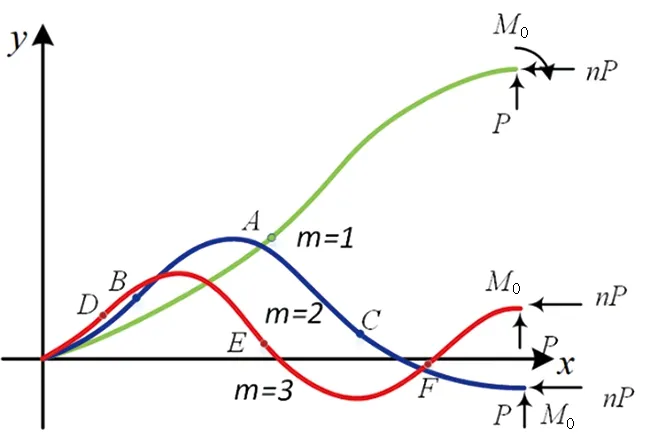
圖7 懸臂梁的大變形彎曲模式Fig.7 Large deformation bending mode of cantilever beam

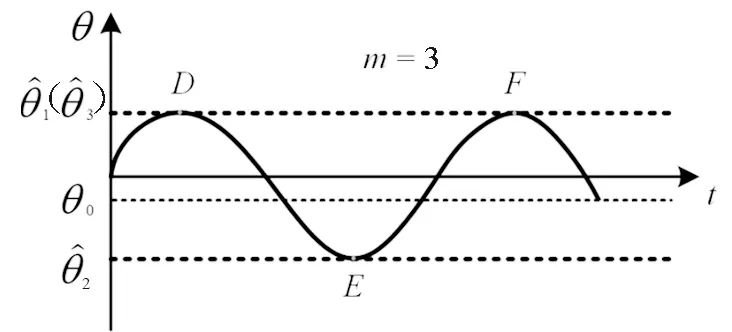
圖8 彎曲梁角度θ的變化Fig.8 Bending beam angle θ change
(11)
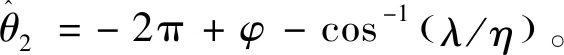
(12)
第一和第二類不完全橢圓積分定義如下:
(13)
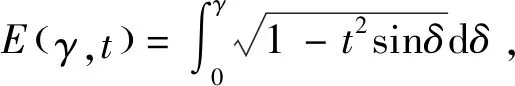
(14)
式中:γ為振幅;t為橢圓模。當γ=π/2時,變為第一、第二類完全橢圓積分,由于橢圓積分的限制,橢圓積分被劃分為兩部分|γ|>η和|γ|≤η。
當|γ|>η時,變形曲線呈單調變化[22],因此沒有拐點(m=0),此時
(15)
式中:
當|γ|≤η,彎曲曲線可以有任意多個拐點(m≥0),此時
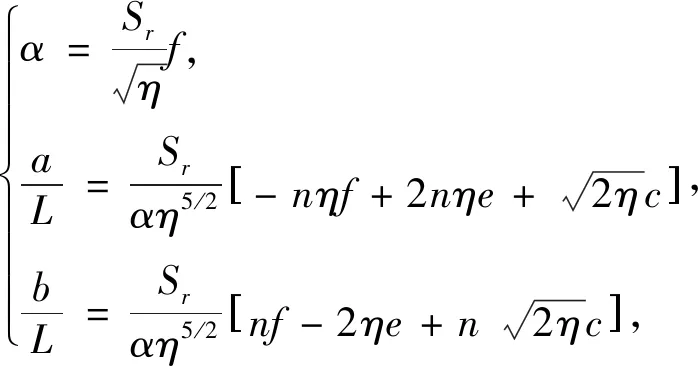
(17)
式中:
式(15)—式(18)中包括7個未知數:3個負載參數(α,k,n)、3個彎曲參數和1個形狀參數(m)。計算時,應首先明確傾斜梁的彎曲模式即拐點數目。當拐點數目m=0時,變形可以通過式|γ|>η或|γ|≤η求解;當拐點數目m≥1時,可以通過式(17)、式(18),在其他的6個參數中任意給定其中3個,另外3個就可以得到求解。
2 模型仿真分析
2.1 雙穩態梁模型的仿真分析
圖4所示的雙穩態梁機構中,設L為傾斜梁的長度,β為傾斜梁與水平方向的夾角,h為傾斜梁的厚度,w為平面外寬度,d為兩個傾斜梁的間距。采用有限元分析軟件Workbench對雙穩態梁的參數進行建模分析,結果如圖9—圖12所示。
由圖9可知,隨著角度的增大,機構的負剛度也隨著增大,同時傾斜角度的增大也使得機構的負剛度特性范圍變大。由圖10可知,隨著長厚比的減小,雙穩態梁的剛度在增加。由圖11可以看出,傾斜梁的間距對傾斜梁特性的影響比較小,一般根據機構的尺寸來選取合適的傾斜梁間距。由圖12可知,傾斜梁寬度的增加使得傾斜梁的負剛度增加,且三條曲線相交于一點;雖然傾斜梁的寬度不同,但彈力方向變化的臨界點處于同一位置,且負剛度機構的負剛度特性范圍也是一致的。
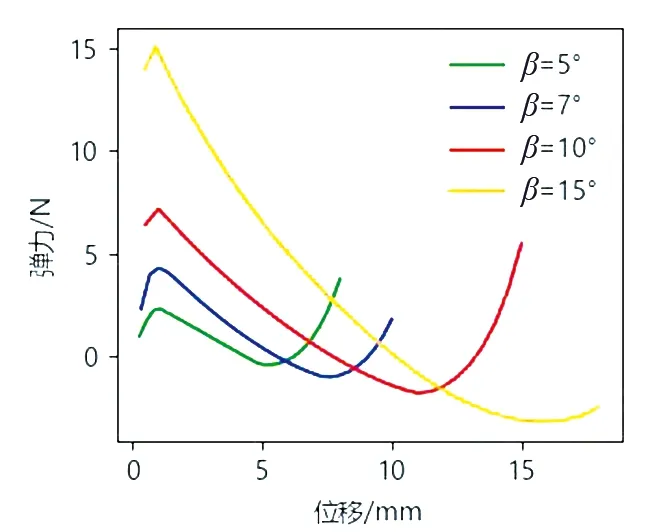
圖9 角度β對雙穩態特性的影響Fig.9 The influence of the angle β on the bistable characteristics
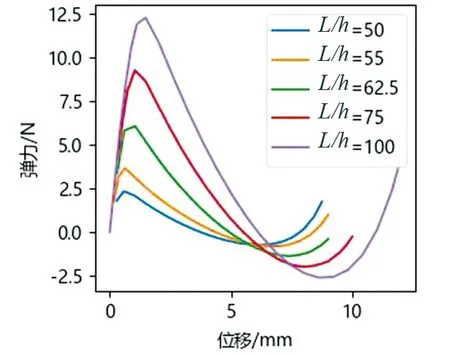
圖10 長厚比對雙穩態特性的影響Fig.10 The influence of the length-to-thickness ratio on the bistable characteristics
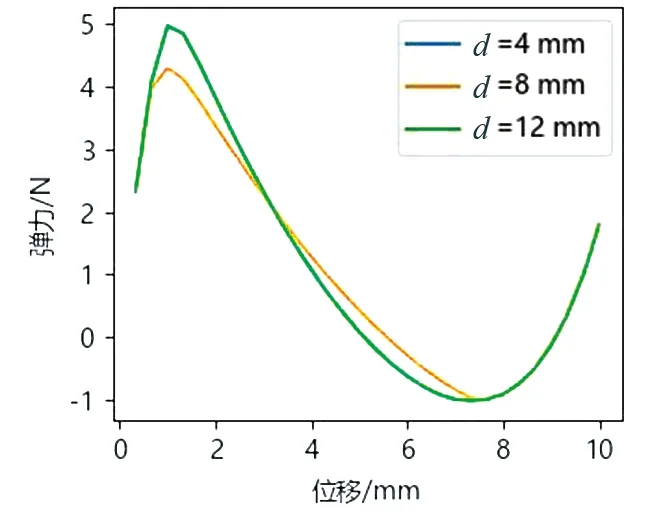
圖11 間距對雙穩態特性的影響Fig.11 The influence of the spacing on the bistable characteristics
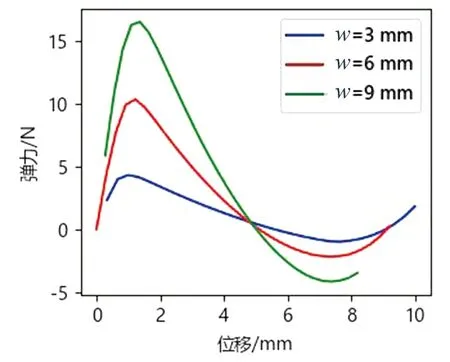
圖12 平面外寬度對雙穩態特性的影響Fig.12 The influence of the out-of-plane width on the bistable characteristics
綜上所述,雙穩態梁的參數對負剛度特性的影響各不相同。雙穩態梁的傾斜角度β、長厚比L/h、傾斜梁的寬度w對雙穩態梁的特性有較大影響,雙穩態梁的間距d對雙穩態梁的特性影響較小。
2.2 恒力機構的仿真分析
利用仿真軟件Workbench對恒力機構進行仿真分析,材料使用ABS樹脂塑料。首先設置合適的邊界條件,然后給恒力機構施加5 mm的位移,得到的整體變形圖如圖13所示。從圖13可以看出,恒力機構的最大變形為6.200 8 mm,在恒力機構的最大變形范圍之內。
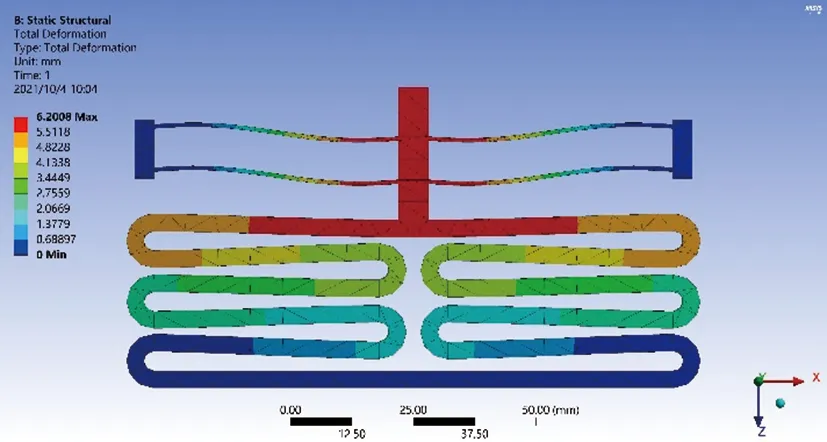
圖13 恒力機構的整體變形圖Fig.13 Total deformation diagram of constant force mechanism
圖14為恒力機構的等效應力圖,從圖14中可以看出,整體機構的最大應力為11.785 MPa,最大應力在ABS的許用應力2 GPa之內,并且恒力機構的整體應力分布均勻,應力集中現象出現較少。
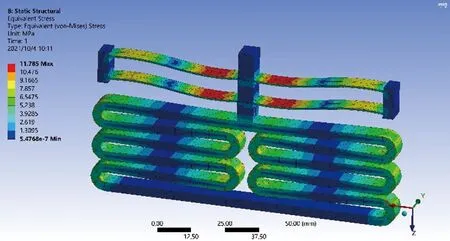
圖14 恒力機構的等效應力圖Fig.14 Equivalent stress of constant force mechanism
圖15為柔順恒力機構的恒力特性圖,從圖15中可以看出,當施加的位移從0開始至1.3 mm時,機構呈現正剛度機構特性;位移大于1.3 mm后,機構開始呈現出恒力機構特性,恒力值大約為6.2 N,恒力特性范圍從1.3 mm至3.2 mm;位移大于3.2 mm后,恒力機構再次呈現出正剛度特性[23]
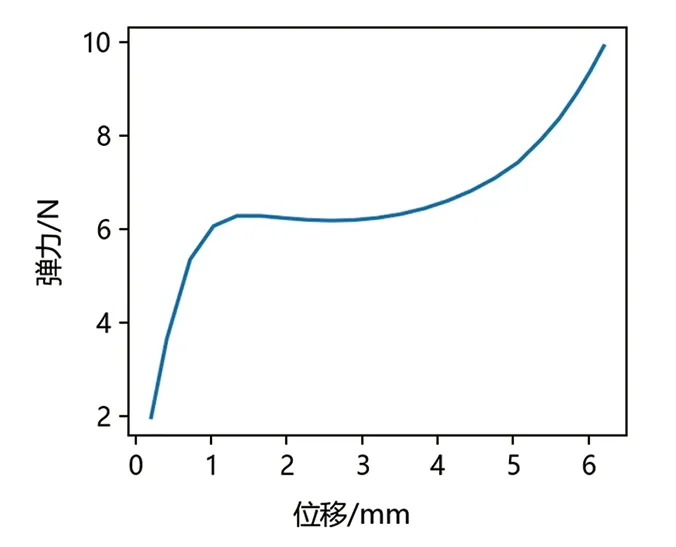
圖15 恒力機構特性Fig.15 Constant force mechanism characteristics
3 結束語
本文設計了一種新型的恒力機構,對負剛度機構即雙穩態機構的參數進行了對比分析,明確了各參數對負剛度機構特性的影響程度,同時對恒力機構進行了有限元仿真分析。仿真結果表明,所設計的柔順恒力機構有約2 mm恒力范圍且恒力大小約為6.2 N。本文所設計的柔順恒力機構恒力范圍較小,且并沒有對恒力的可調性能進行測試,今后可進一步擴大恒力范圍并對恒力機構的恒力可調性能進行測試。

