基于模糊故障樹和灰色關聯算法的CASS污水系統分析
魯明,吳志光
(池州職業技術學院 機電與汽車系,安徽 池州 247000)
隨著“中國制造2025”和“工業4.0”計劃戰略的提出,國內外專家和學者開始重視利用智能技術解決故障診斷問題。污水處理是一個復雜的、多變量耦合、非線性的生化過程,當污水處理廠發生故障時,出水水質指標達不到標準,會造成二次污染。因此,如何解決和實現污水處理系統的故障診斷與識別是一個不可回避的難題。
近年來,大數據技術和多元統計理論的故障診斷方法得到了廣泛的應用,特別是在機械、風電、航空技術、數控機床、化工、醫藥等領域,正朝著高效率的方向發展,因此必須依靠故障診斷知識和專家系統為其保駕護航。由于現代設備診斷規模大,每臺設備可能出現多個故障點,數據采集頻率高,因此必須通過檢測故障診斷來獲取海量數據,為此國內外專家付出了艱辛的努力,取得了巨大的研究成果。例如,許玉格等[1]將核理論與極限學習機相結合,對污水處理過程進行在線診斷。魯明[2]將神經網絡與PCA方法相結合,利用神經網絡對關鍵出水指標值進行預測,消除了污水處理過程中的非線性和動態影響,該方法優于傳統的PCA方法。王彤等[3]提出了基于模糊灰色關聯的汽車驅動橋系統故障樹分析方法,將模糊理論和灰色關聯算法有效地結合起來,分析了基于模糊灰色關聯的故障樹建立過程,并將其應用于汽車驅動橋系統,證明了系統的可靠性。Cai等[4]提出了一種基于故障樹的可靠性風險分析方法,解決了模糊和不確定信息的風險建模問題。Zhou等[5]提出了一種基于PCA的貢獻圖方法來識別與故障相關的關鍵變量。Sang等[6]提出了一種基于KPCA的故障識別方法,其構建魯棒誤差故障識別方法的基本思想是當重構變量為故障變量時,該變量的故障指數小于非故障變量的故障指數,實踐證明該方法準確、效率高、應用廣泛。上述研究都是對系統的模糊性進行分析,但是污水系統就是一個模糊性、復雜性、同時又具有灰色性的系統,由于故障信息的缺失,使得故障事件之間的相關性存在不確定性。
本文研究的是具有強非線性、先驗知識少、模糊性和灰色性的非平穩CASS(cyclic activated sludge system),也稱周期循環活性污泥法工藝工業廢水處理過程,提出一種基于模糊灰色關聯的污水處理系統故障樹分析方法,將灰色理論與模糊數學理論相結合,采用模糊灰色關聯的故障樹分析方法,用三角模糊數表示污水處理底部事件的概率。
1 污水處理故障建立與分析
1.1 故障樹分析(FTA)
故障樹分析(FTA)是通過演繹的方法逐級分層找出故障的可能發生原因,以最后找到最基本的原因為止。該方法將系統中可能發生的故障或最不期望發生的事件作為故障樹的頂事件(包括環境、軟硬件、人為因素等),導致故障狀態的所有可能原因作為中間事件,導致中間事件發生的最終原因作為底事件,然后通過事件之間的邏輯關系,建立系統故障的數學模型。其中,割集是指故障中一些底部事件的集合[7]。當這些底部事件有一個發生時,頂部事件必然發生。最小割集是指將集合中所含的底事件去掉1個就不能成為割集,一般來說,最小割集可以用下行法找到,即從頂事件開始,逐層找到割集,遇到“與門”時,增加割集的階數,遇到”或門”時,增加階級的個數。具體方法是:從故障樹的頂事件開始,依次用頂部的上一個事件替換下一個事件;當遇到“與門”時,將事件橫向連接在一起,當遇到“或門”時,將事件豎直串聯接在一起,直到所有邏輯門都被底事件替換為止;這樣,表的最后一列中的每一行都是故障樹的割集,然后對割集進行比較,進行元素的合并和剔除,得到故障樹的全部最小割集。
1.2 模糊數
模糊數的表示方法有多種形式,教材和文獻中最常見的方法大概分為三類:三角模糊數、梯形模糊數和正態模糊數[8],本文采用的是三角模糊數,三角模糊數的隸屬函數如圖1所示。圖1中Up(x)為x的隸屬函數,a和b為模糊數的下限和上限。
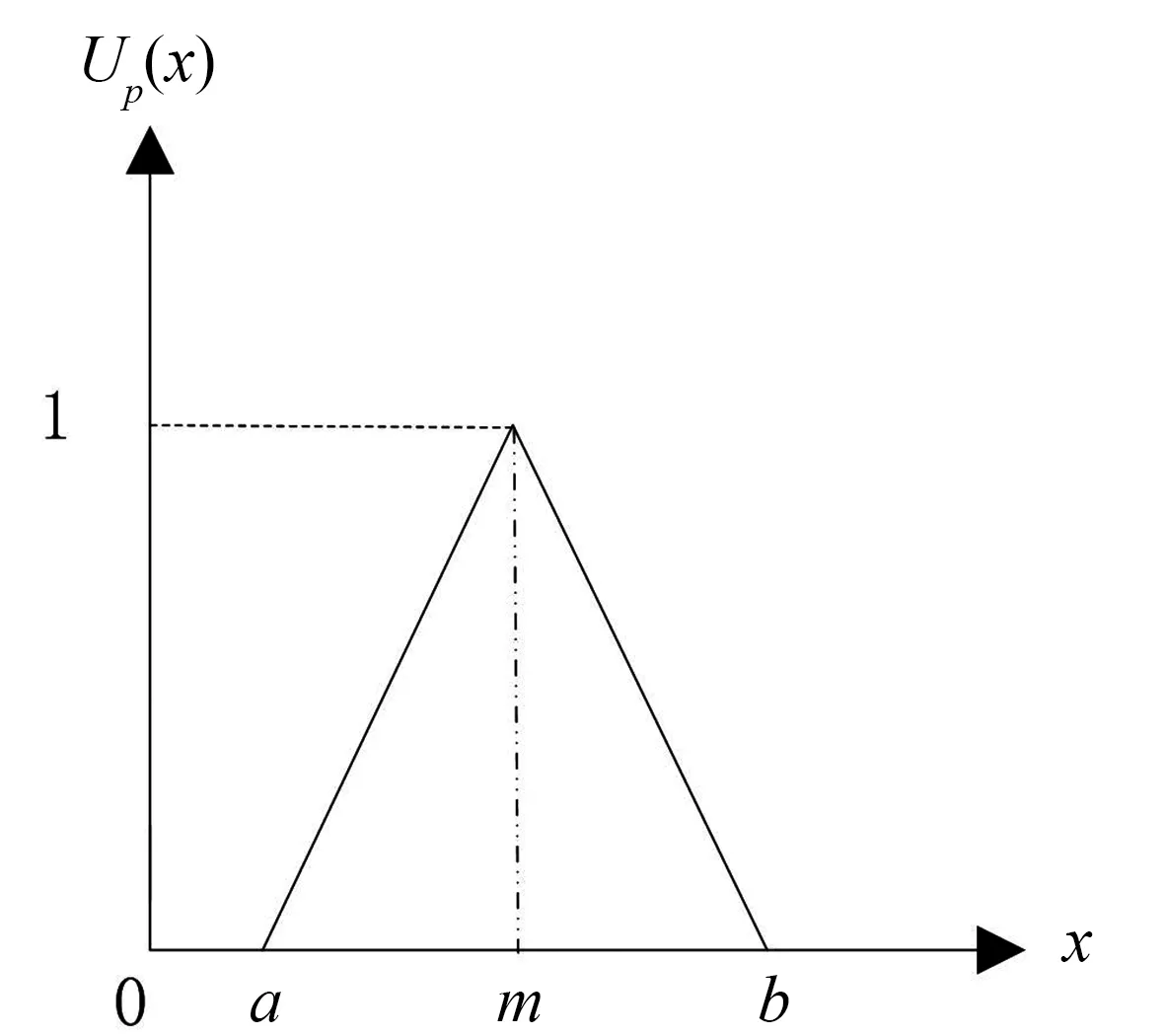
圖1 三角模糊隸屬函數Fig.1 Triangular fuzzy membership function
通常在分析大型污水處理系統時,由于系統的復雜性和運算量大、過程復雜等原因,很難求解出頂事件發生的概率,但是可以運用三角模糊數解決這一難題,它的特點是計算和結構簡單,對定量分析有著重要作用。其隸屬函數表達式為
(1)
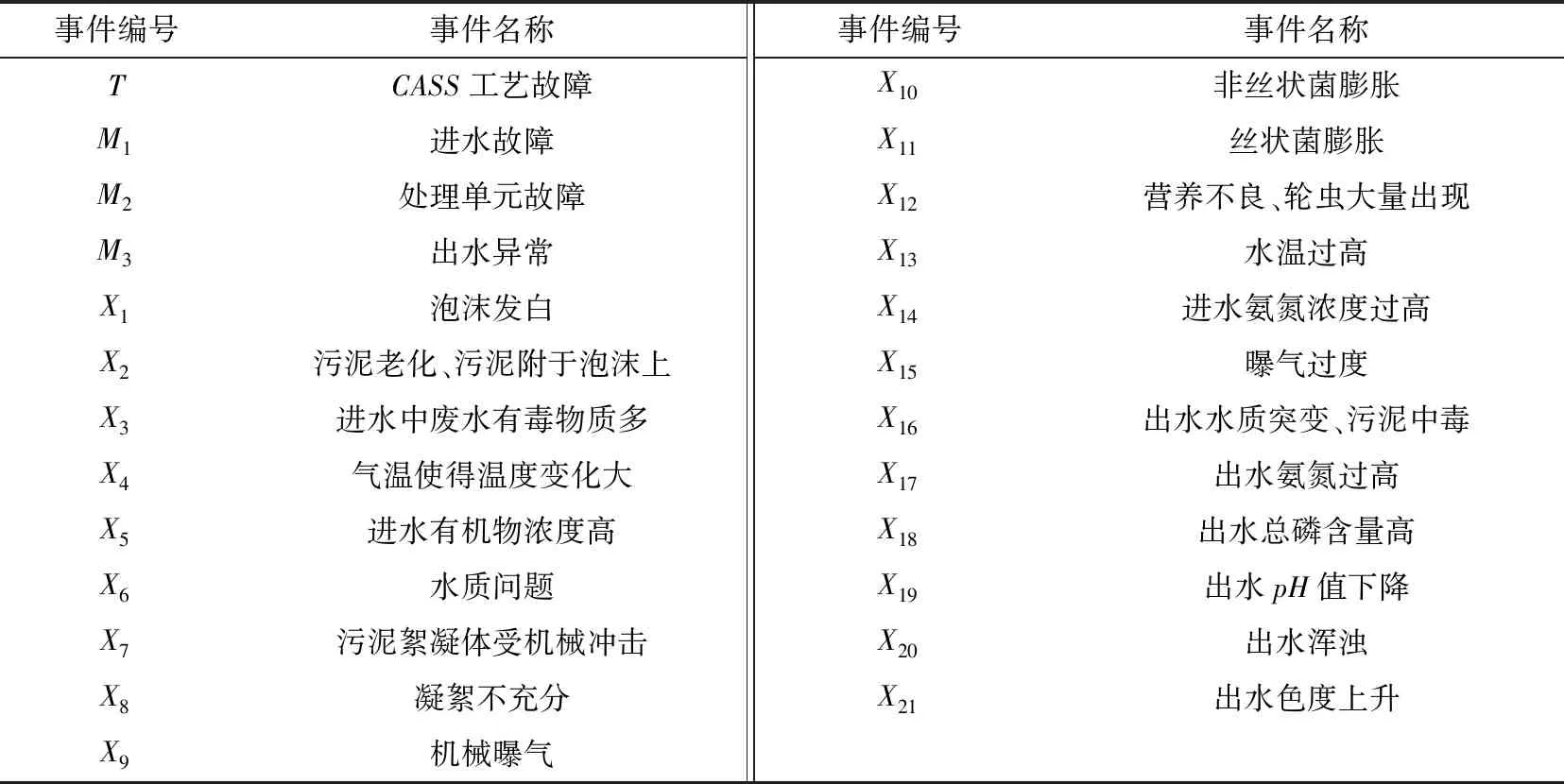
則設底事件xi(i=1,2,3,…,n),底事件發生的概率Pxi=(m-a,a,m+b),其中a,b為Pxi的上下限,m為底事件發生概率的中值,有0 (2) (3) 根據函數H(x)=H(x1,x2,x3,…,xn)以及底事件發生的概率,可判斷頂事件T發生的概率:PT=(aT,mT,bT)。 (4) 式中:當第i個最小割集里包含的基本事件都不發生時,頂事件仍然能發生的概率PT=(aT,mT,bT);記模糊概率的中值為mT0,則頂事件在底事件xi沒有發生故障時,仍會發生的概率PTi=(aTi,mTi,bTi)。 灰色系統就是利用數據信息量少、信息不全、各個元素之間無相關性的特點,實現對部分信息確切描述和理解。對于大型的污水處理系統而言,它的系統存在模糊性和非線性,在進行可靠性分析時,各個故障樹之間、故障事件和頂事件之間的關聯性也不確定[9];因此,將關聯分析引進到故障樹分析中很有必要。灰色關聯分析就是通過灰色關聯序列比較不同元素之間的強弱關系,將故障樹中各個最小割集的模糊重要度均值化處理,作為灰色模型的子序列,其表達式為 XT=[XT(1),XT(2),…,XT(n)]= (5) (6) 則灰色模型的子序列可構成的矩陣為 (7) 為了診斷出各個元素的影響因素,將構成的矩陣Xm和XT進行灰色關聯度的比較,通過關聯度的計算,將關聯度進行排序,就能得出不同故障模型對頂事件影響的重要程度。 在構成的兩個矩陣Xm和XT中,將對應于第i個基本事件的差值的絕對值作為差序列,即 ΔMT(i)=|Xm(i)-XT(i)|。 (8) 在針對多元矩陣序列分析時,計算關聯系數的公式為 (9) 式中ρ為分辨系數且0<ρ<1,通常取ρ=0.5。灰色關聯度是表示兩個灰色系統之間相似性的指標,變化范圍為[0,1],越接近1影響越敏感,反之就越不敏感。由于關聯度的數量多、信息分散,所以在計算其關聯度時按照平均值法求解比較方便,可以得出 (10) 最后,根據求解的γk對最小割集進行排序,求出的灰色關聯度越大,則最小割集對故障影響越敏感;反之則越不敏感。 在分析故障樹時,底事件的發生會影響頂事件的發生,任何與最小割集結合的割集都是導致頂事件發生的最小割集。最小割集中的基本事件發生時,那么頂部事件一定發生[10]。對于一個故障樹系統而言,設總共有M個元件,系統發生故障記為故障樹的頂事件并記為T,構成的元件為底事件記為X1,設系統的元件有正常和非正常兩種狀態,分別用0和1表示,則 (11) 然而,由于頂事件的狀態是底事件的狀態函數,可以用T(x)=T(x1,x2,…,xn)描述,則 (12) 根據上述對故障樹的描述,本文以污水處理系統的CASS工藝作為研究對象。CASS工藝的優點是能去除污水中的可降解有機物,同時也能去除易降解的可溶性有機物,促進系統中絮凝細菌的生長,提高系統運行的穩定性和可靠性。CASS工藝系統的運行分為4個不同階段,即進水階段、曝氣階段、沉淀階段和閑置階段,在此期間,污泥不斷循環運行。池內污泥經過好氧和厭氧兩種過程,有利于除磷菌的生長。在曝氣階段,通過硝化反應實現除磷脫氮;在非曝氣階段,還存在反硝化作用,將活性污泥帶回生物選擇都不在考慮的故障范圍之內[11],即省去了在故障樹設計中人為因素導致的故障。 根據資料和某污水處理廠的實時統計顯示,CASS污水工藝故障如圖2所示,各種故障事件見表1。 表1 故障事件表Tab.1 Failure event table 如圖2所示,從故障樹的底事件開始,最底層的每一個基本事件都是割集,只有當底事件都發生時,頂事件才會發生,但是如果隨意刪除一個基本事件,該割集就不是最小割集。由此可以得出故障樹的最小割集是21個,分別為: 圖2 CASS污水工藝故障樹Fig.2 CASS wastewater process fault tree K1={X1},K2={X2},K3={X3},K4={X4}, K5={X5},K6={X6},K7={X7},K8={X8}, K9={X9},K10={X10},K11={X11},K12={X12}, K13={X13},K14={X14},K15={X15}, K16={X16},K17={X17},K18={X18}, K19={X19},K20={X20},K21={X21}。 頂事件是所有底事件和的表達形式,則該故障樹可表示為H(X)=M1+M2+M3=X1+X2+X3+X4+X5+X6+X7+X8+X9+X10+X11+X12+X13+X14+X15+X16+X17+X18+X19+X20+X21。如果對系統進行全部分析則較為復雜,因此本文僅對出水異常事件作為頂事件來進行分析,可知M3包含了6個最小割集,分別是{X16},{X17},{X18},{X19},{X20},{X21}。 統計近5年污水處理廠的數據以及可能發生故障的概率。根據經驗可知,發生出水異常故障的概率為10%,且該故障概率中35%為水質突變、污泥中毒,表現為X16事件;35%為有機物含量過高,具體表現為X17和X18事件;20%為出水的pH值含量下降,具體表現為X19事件;10%為出水水質顏色的變化,具體表現為X20和X21事件。根據以上統計,采用三角模糊數表示上述事件的概率,得出如表2所示的故障發生概率。 表2 故障發生概率Tab.2 Probability of failure 根據式(2)和式(3)可以求出三角模糊概率PT=(0.109 78,0.164 53,0.204 37),進一步可以求出M3事件的概率模糊中值mTz=0.164 29,根據式(4)和式(5)可以求出最小割集。由于設計的故障樹只有或門,所以每一個基本事件只有一個割集,各個割集的模糊重要度依次為(0.031 38,0.031 38,0.031 38,0.025 41,0.014 57,0.014 57)。 由上述實例得出底事件為6個,即m=6,在特征矩陣最小割集中所含有的底事件均取1,其余為0,這樣可得到矩陣 (13) 根據故障樹每個底事件發生的概率,可以獲得每個底事件的關聯重要度(見表3)組成檢測模式的向量,即 表3 關聯重要度Tab.3 Relevance importance (14) 把各個底事件的模糊重要度均值后,再將標準模式中的向量進行量化處理,可以得到待檢測模式向量 (15) 以Z[J]為參考序列,X為比較序列,根據式(6)和式(7)可以計算出各個灰色關聯度,采用平均值法,取Δmin=0,Δmax=1,ρ=0.5,得出{γ16,γ17,γ18,γ19,γ20,γ21} ={0.713 20,0.708 25,0.714 14,0.695 25,0.695 25,0.674 14}。根據上述結果,對構成中間事件M3出水的6種模式的最小割集灰色關聯度依次進行排序,可以得出相應的結果:γ16>γ18>γ17>γ19=γ20>γ21。可以看出γ16水質突變、污泥中毒對出水異常影響最大,也是導致CASS工藝污水故障的重要影響因素之一。而在M3事件中,γ21出水色度上升對出水異常影響最小,符合污水處理廠長期數據統計的規律。經過灰色關聯度的分析可以得出如下結論:水質突變、污泥中毒,出水氨氮過高,出水總磷含量高對出水異常故障影響最大,所以在檢測時,需要進一步加大檢測精度,改善工藝水平。 本文利用灰色關聯算法和三角模糊數解決了故障樹難以獲得準確概率的問題,以及各事件之間關系難以確定和發生故障概率大小問題。根據模糊關聯故障樹的分析算法,首先根據故障樹求出最小割集,然后利用三角模糊重要度求出故障發生的概率,建立灰色關聯模型,通過計算得出最小割集與中間事件和頂事件的灰色關聯度,找出系統的薄弱環節。結果表明,運用故障樹和模糊理論以及灰色關聯算法三者相結合的方法對污水處理的分析是可行的。此算法比傳統BP神經網絡具有更好的故障預測效果,準確度高、穩定性好。1.3 模糊重要度

1.4 灰色理論分析
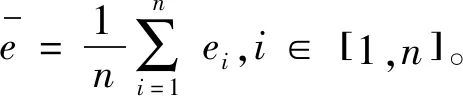
1.5 灰色關聯的計算
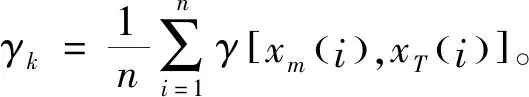
1.6 灰色關聯分析在故障樹中的應用

2 CASS污水工藝處理系統的故障樹分析
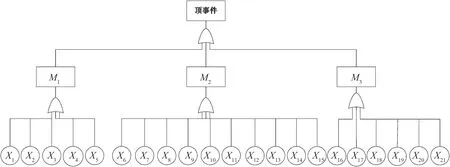
2.1 模糊概率的計算
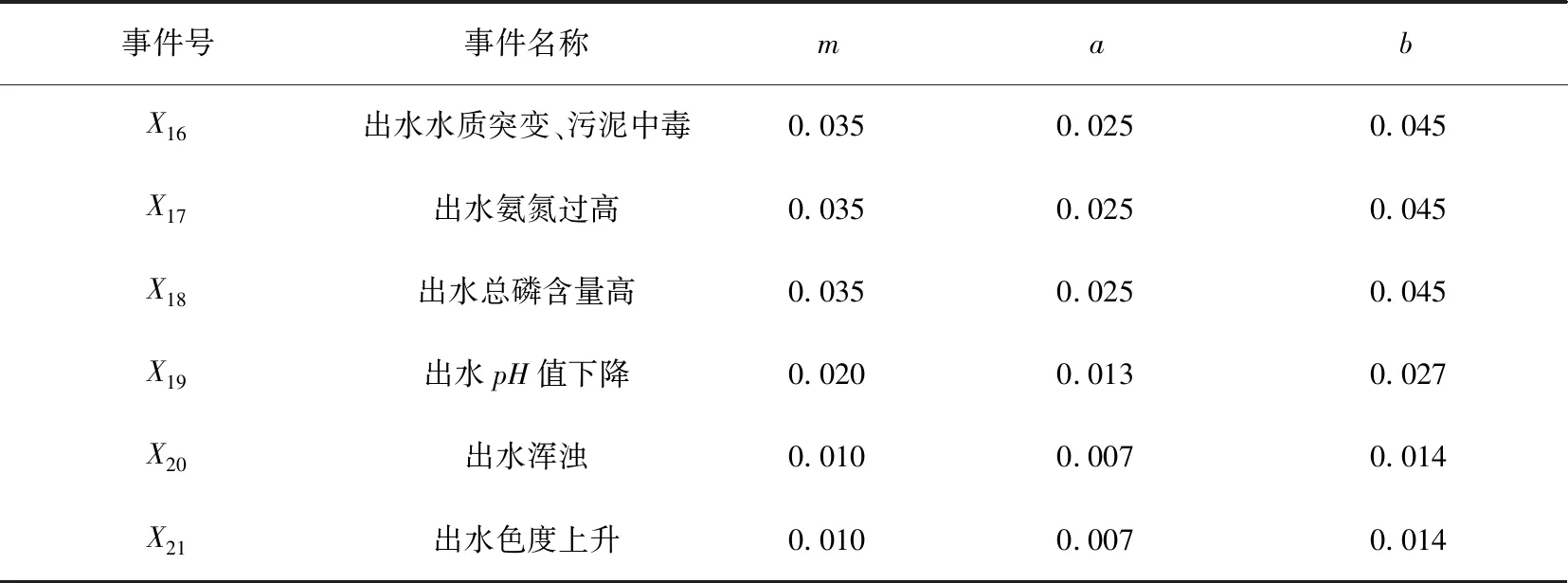
2.2 特征值的故障矩陣
2.3 計算關聯系數
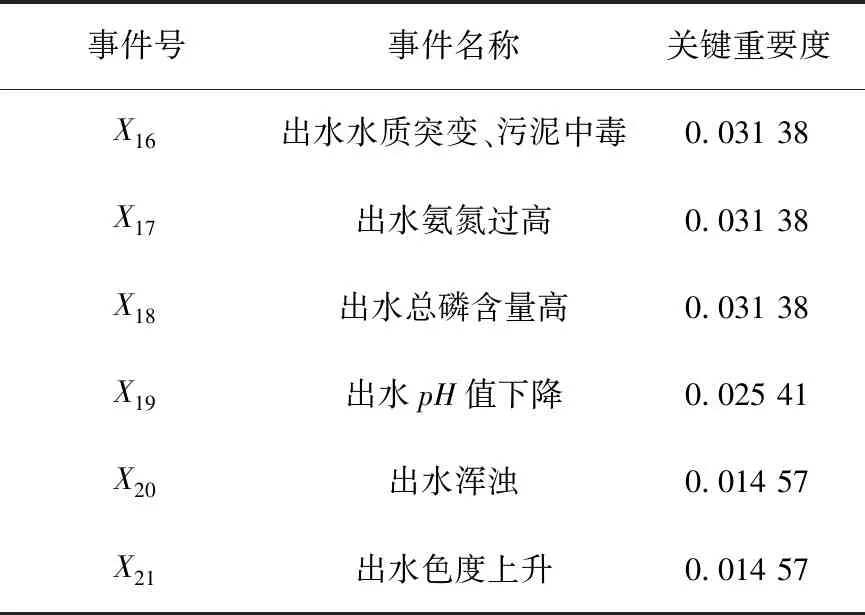


3 結束語

