量子遺傳算法對砂類邊坡穩定性敏感度的分析

王海龍，劉麗峰

(山東理工大學 建筑工程學院,山東 淄博 255049)

邊坡穩定性問題是巖土工程界長久以來的經典技術問題，迫切需要尋找和開發出分析與應對方案[1]。楊俊[2]提出了一種基于多種群遺傳算法的邊坡研究方法，將遺傳算法應用到邊坡穩定性問題的分析上，構建了一個廣泛且多功能通用的穩定性分析模型；胡培強等[3]利用強度系數折減有限元法，對邊坡的多種參數建立影響因子方程，得出邊坡穩定性不同影響因素的數值對比，其使用軟件進行分析，結果具有可靠性和便捷性。王婭娟[4]利用Matlab軟件以轉角為搜索依據對邊坡進行破裂面搜索，編寫了可靠性與敏感度分析程序，程序開源可復刻性高。

由于傳統的遺傳算法收斂速度較慢，且容易陷入局部最優解，對于邊坡穩定性一類擁有多元變量的解算，需要極力避免局部最優情況。針對這類問題，在傳統遺傳算法中引入量子比特與量子旋轉門的概念，使種群編碼與進化策略上與遺傳算法有所不同，通過量子位同時表達多個染色體狀態信息，再通過量子旋轉門對量子比特的相位進行變換，實現其概率幅更新，以達到基因變異的效果，增加其進化的復雜度，使易陷入局部最優解的情況得以改善。

1 邊坡參數的敏感度計算

1.1 影響程度的數學表達

邊坡穩定系數主要與邊坡高度h、坡度/坡角β、土體容重γ、土體黏聚力c、土體內摩擦角φ等參數有關，分析參數對邊坡穩定性的影響程度可構建敏感度方程如下：

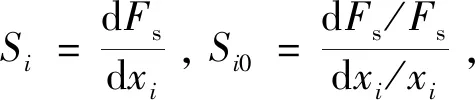
(1)

式中：Si是參數影響系數；Si0為無因次影響因子；Fs為邊坡穩定系數；xi為任意參數。

1.2 邊坡穩定性分析

設坡高為h，任一破裂角為α，坡角為β，土體重度為γ，L為破裂面邊長，可表示為L=W/sina。邊坡滑動體截面ΔABC重力可記作W，W=SΔABC×γ，滑坡體受重力分力，從而產生沿破裂斜面下滑的力F下，而坡體內部的內摩擦力等內應力則產生一個與下滑力方向相反沿斜面向上的妨礙下滑的摩擦力，記為抗滑力F抗，F下與F抗在物理關系上可作如下表示：

F下=Wsinα,F抗=Wcosα×tanφ+c×L，

(2)

此時Fs即可表示為

(3)

式中c為土體黏聚力。

以此為基礎，可以將邊坡最危險滑動面檢索問題設計為多元函數尋優問題，而邊坡最危險滑動面即為函數尋優的結果。根據參數模擬變化，可進一步推算該邊坡在不同條件下的破裂角與穩定性。

2 研究方法

2.1 量子比特編碼

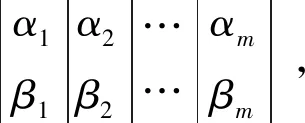
染色體的編碼方式通過量子位概率幅進行表達：

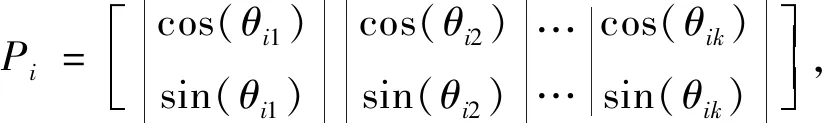
(4)

θij=2π×rand,i=1,2,…,n,j=1,2…，k，

(5)

式中：θ為量子比特的相位；N為染色體數量；k為量子位的位數；rand為[0,1]范圍內的隨機數。

2.2 量子旋轉門

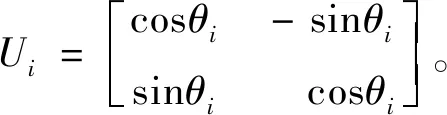
3 算例分析

3.1 邊坡穩定性對邊坡參數的敏感度實例分析

根據公式(3)，可以將邊坡穩定性問題簡化為一個以破裂面和穩定系數為基準的多元函數尋優問題，并以邊坡極限平衡條件下的穩定系數方程建立邊坡的數學模型。通過QGA進行尋優，可以得出在不同破裂面的穩定系數以及同一破裂面在不同參數波動的條件下的穩定系數變化。

如圖1、圖2所示，坡高和土體容重對邊坡穩定性具有負相關作用，但邊坡穩定性對土體容重的敏感度較低。坡度與坡高的增加都會直接導致任一破裂體的破裂角增大，下滑力顯著提升。容重的上升則會導致破裂體下滑力的增加，使邊坡穩定性降低。

圖1 土體容重對邊坡穩定性影響程度曲線Fig.1 Curve of influence degree of soil bulk density on slope stability

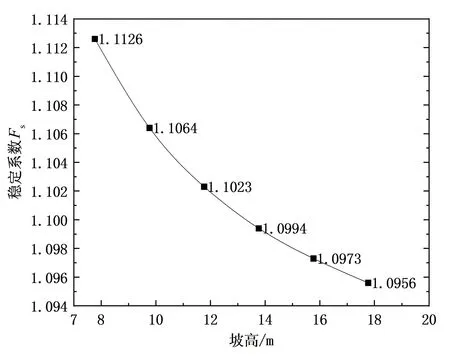
圖2 邊坡高度對邊坡穩定性影響程度曲線Fig.2 Curve of influence degree of slope height on slope stability

通過單個邊坡與單個數據的約束變異無法完全顯示各參數變化時對邊坡穩定性的影響程度，因此，還要讓邊坡對不同參數改變之間產生的敏感度進行對比分析，以得出進一步的結論。

黏聚力和內摩擦角增大均會引起邊坡穩定性的增加，反之二者減少也會削弱邊坡的穩定性。那么在同等變化條件下，約束內摩擦角的黏聚力變化導致穩定系數變化量為Δc，約束黏聚力的內摩擦角變化導致穩定系數的變化量為Δφ，對比二者的敏感度，同時不斷改變邊坡坡度，可以得出不同坡度條件下的敏感度。通過計算，坡角為26.56°的條件下邊坡穩定系數對二者的敏感度如圖3、圖4所示。

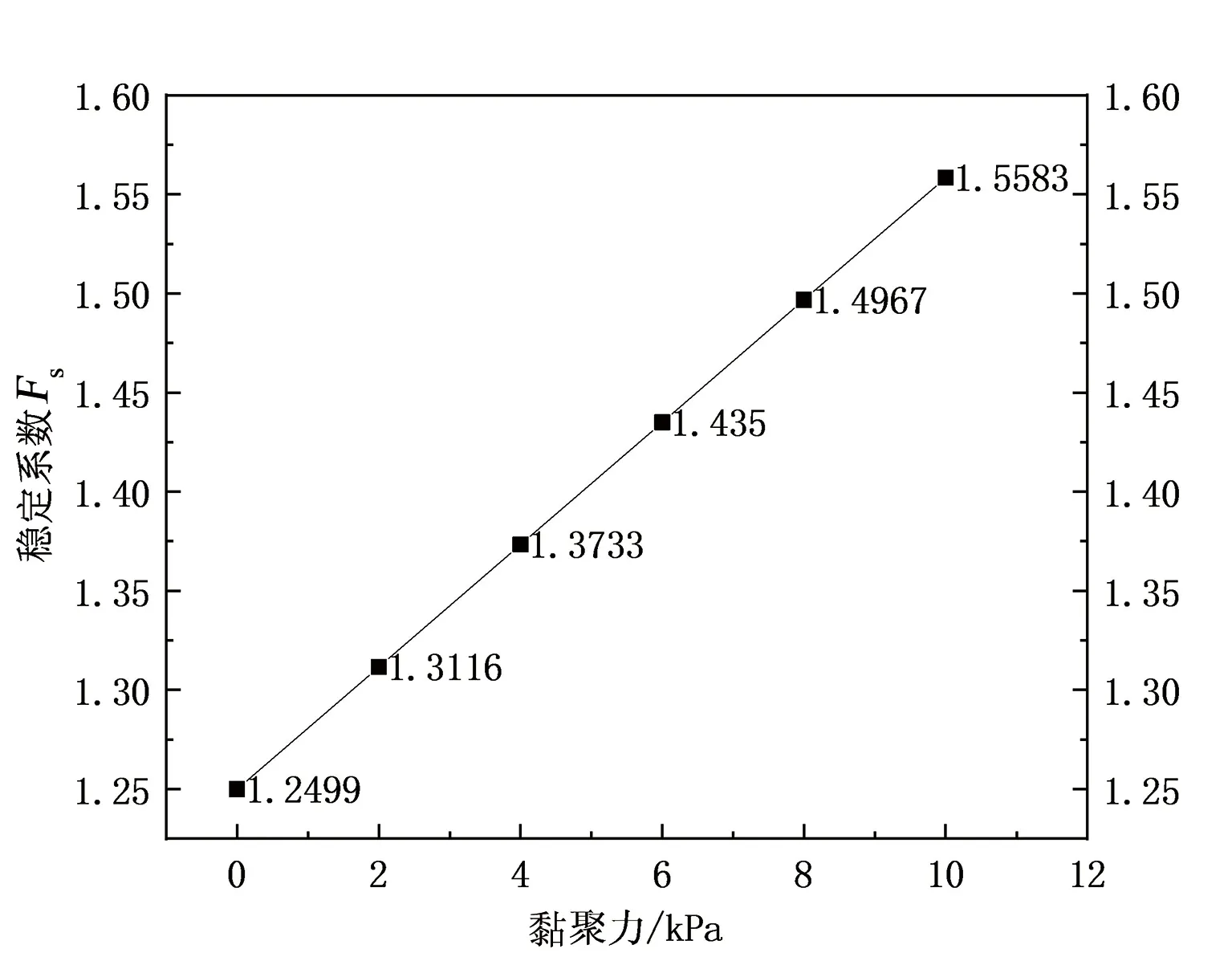
圖3 土體黏聚力對邊坡穩定性影響程度曲線Fig.3 Curve of influence degree of soil cohesion on slope stability

圖4 土體內摩擦角對邊坡穩定性影響程度曲線Fig.4 Curve of influence degree of internal friction angle on slope stability

黏聚力與內摩擦角對邊坡穩定性均具有正相關關系，在此算例同等變異量下，內摩擦角變化時對穩定系數的影響小于土體黏聚力對邊坡穩定性的影響。

3.2 不同容重條件下黏聚力的敏感度發生變化

土體容重的改變，不僅會影響穩定系數，還會影響參數的敏感度。土體容重增加會導致土體抗剪強度增加，提升土體穩定性，也會讓黏聚力對穩定系數的影響程度增加。當容重降低時，雖然在相同條件下穩定系數的改變并不劇烈，但穩定系數對內摩擦角和黏聚力的敏感度發生了變化，影響程度變化如圖5、圖6、表1所示。

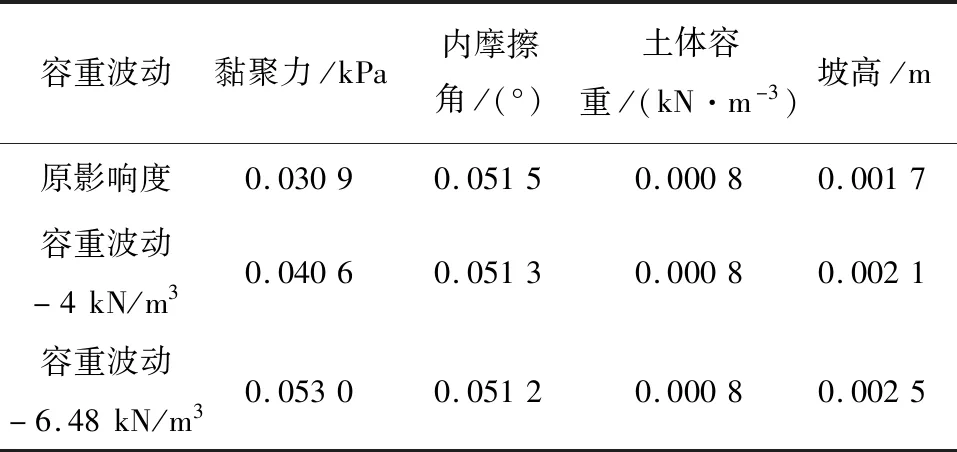
表1 影響程度分析Tab.1 Impact degree analysis

圖5 容重波動后的內摩擦角敏感度變化曲線Fig.5 Sensitivity curve of internal friction angle after bulk density fluctuation

圖6 容重波動后的黏聚力敏感度變化曲線Fig.6 Cohesion sensitivity curve after bulk density fluctuation

容重降低了4 kN/m3時，同等變異程度下，內摩擦角對穩定系數的影響度由0.051 5降低至0.051 3，

呈現微弱正相關變化。黏聚力對穩定系數的影響度由0.030 9增至0.040 6，在土體容重發生變化時，黏聚力對邊坡穩定性的影響度呈現負相關變化。

土體容重的降低會導致土體抗剪強度降低與坡體滑動力的上升。假設邊坡破裂體下滑力函數F(x)=f(γ)·f(φ)+f(c)，其中：f(γ)為破裂體的質量，是土體容重γ與土體體積的乘積；f(φ)為土體內摩擦角φ的正切；f(c)為土體黏聚力c與破裂體斜邊長度的積。邊坡任一破裂體的容重降低即f(γ)·f(φ)降低時，會導致內摩擦角對穩定系數影響程度的降低，即內摩擦角對邊坡穩定性的影響程度與土體容重呈正相關關系。土體黏聚力對穩定性的影響則表示為對破裂體質量函數的和，即當土體容重降低時，內摩擦角的影響程度占比減小，使黏聚力對穩定系數的影響程度占比增大，即黏聚力對邊坡穩定性的影響程度與土體容重呈負相關關系。

經過計算，在坡高h=9.77 m，坡角β=24.45°，土體容重γ=10.22 kN/m3，內摩擦角φ=20.84°時，黏聚力對邊坡穩定系數的影響度增至0.052 97，此時黏聚力對穩定系數的影響度超過內摩擦角，邊坡參數的主導影響因素由內摩擦角轉變為黏聚力。在實際環境中，降水、路面壓力、地下水位、坡體高度等因素變化時，土體容重并非一成不變，也會導致此類情況的發生。

3.3 與軟件模擬結果對比

文獻[3]提出了一種基于強度系數折減法與邁達斯GTS軟件的邊坡系數敏感度的分析方法，構筑了敏感度曲線模擬函數，并提供了實例計算數據。通過與現有軟件及其實例的對比，可觀察出通過QGA數值模擬進行計算參數敏感度結果的可靠性。在相同實例下，計算的參數平均敏感度得出的結果對比見表2。

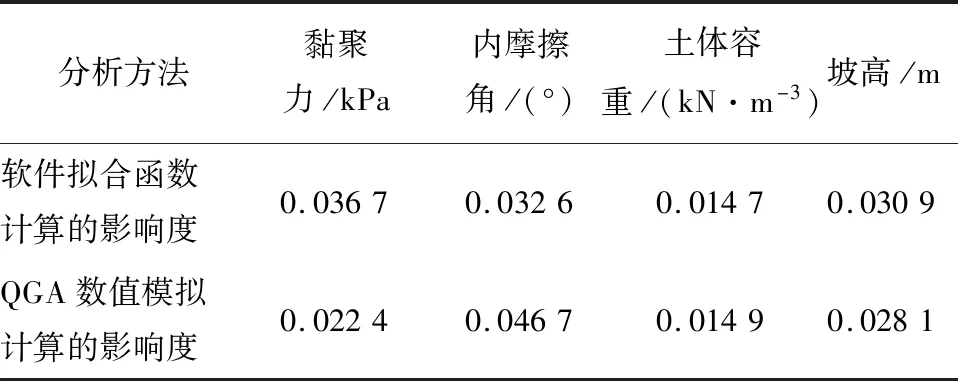
表2 不同分析方法的結果對比Tab.2 Results comparison of different analytical methods

文獻[3]中提供的坡高波動區間為8 m至14 m。如圖7所示，在這個區間內，QGA數值模擬與邊坡分析軟件的擬合函數的結果大致相同，最大差異度小于2%,但根據函數擬合額外增加波動區間、即邊坡高度范圍在小于8 m以及大于14 m后，軟件函數模擬出現了奇異值。根據邊坡穩定性理論，邊坡高度上升會導致邊坡失穩，因此在超出原波動范圍時，軟件函數模擬的結果會出現較大誤差；而在軟件擬合較為正確的區間內，QGA數值模擬與軟件模擬的結果大致接近。

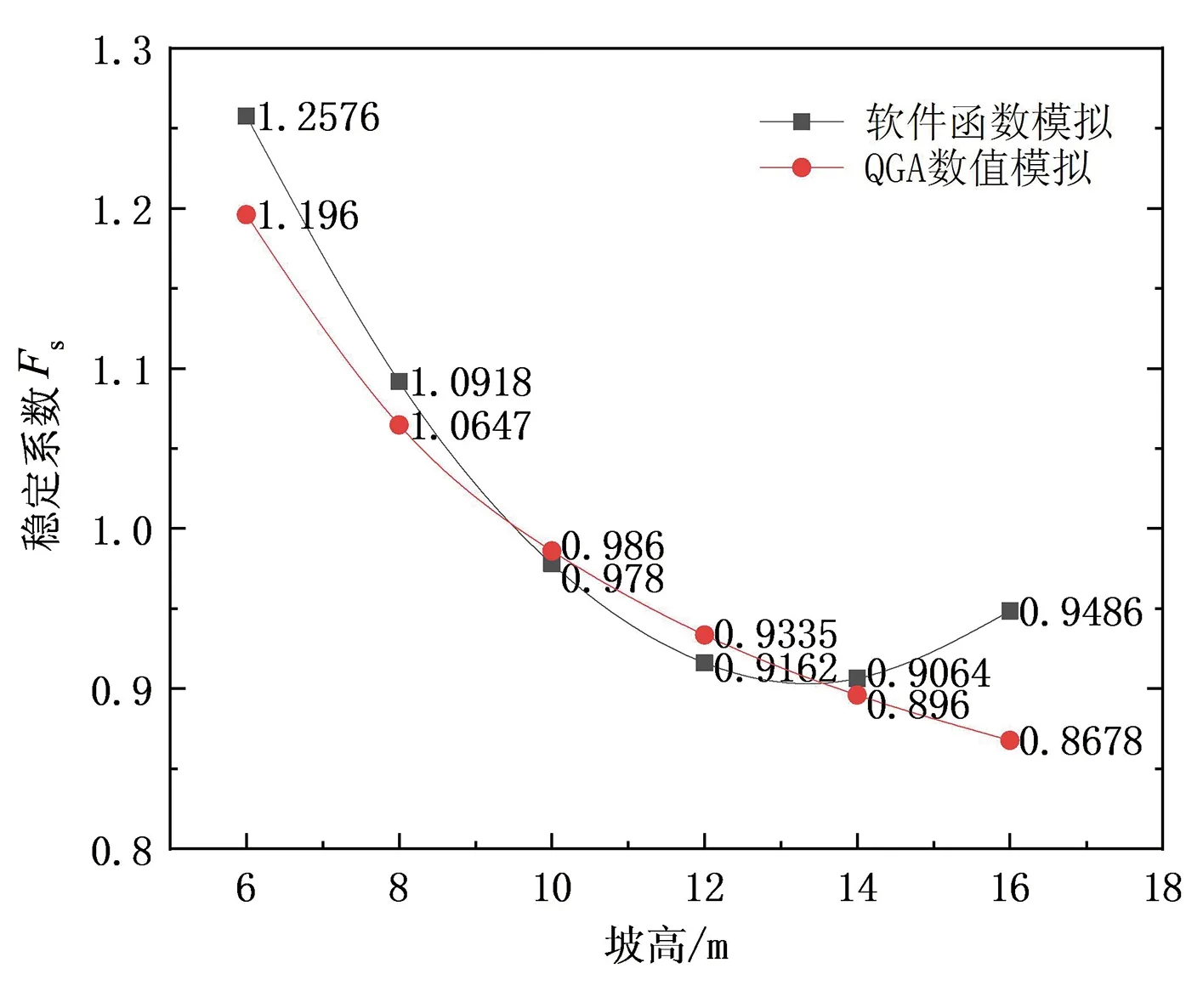
圖7 邊坡高度對邊坡穩定性的影響關系曲線Fig.7 Influence curve of slope height on slope stability

如圖8所示，在分析黏聚力時，QGA出現了差異值。原因可能是：由于土體黏聚力對邊坡土體的其他因素變化響應較大，而本程序在借用文獻[3]算例時，由于土壤性質、函數模型、其他土體參數、搜索方式等的差異，導致了QGA計算的土體黏聚力對邊坡穩定性的敏感度發生下降，實際影響度從0.036 7降低至0.022 4。

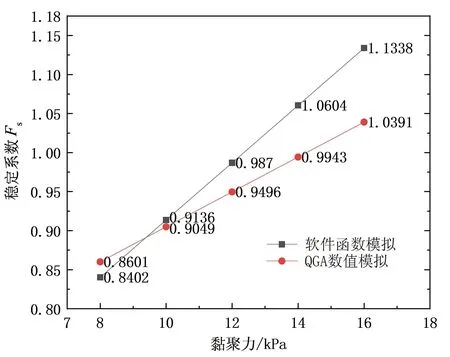
圖8 土體黏聚力對邊坡穩定性的影響關系曲線Fig.8 Influence curve of soil cohesion on slope stability

如圖9、圖10所示，在軟件指定的參數變化區間內，QGA數值模擬和軟件的擬合函數得出的結果具有相似性。

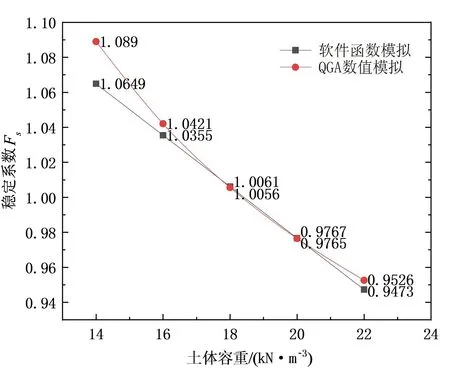
圖9 土體容重對邊坡穩定性的影響關系曲線Fig.9 Influence curve of soil bulk density on slope stability

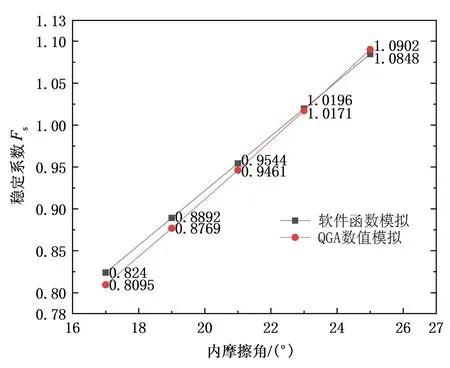
圖10 土體內摩擦角對邊坡穩定性的影響關系曲線Fig.10 Influence curve of soil internal friction angle on slope stability

4 結論

通過量子遺傳算法將邊坡問題進行數值模擬，將影響邊坡穩定性的不同參數之間的敏感度進行分析，并對比了部分參數的敏感度，分析了不同參數在邊坡穩定性上的影響方式，得出以下結論：(1)邊坡穩定系數對土體容重的敏感度較低，但會通過影響其他參數的敏感度進而影響邊坡整體;(2)同等參數條件下，內摩擦角、黏聚力、土體容重對邊坡的影響程度較為均勻，基本呈現線性趨勢，具有一定的可預測性;(3)土體黏聚力和內摩擦角的波動幾乎不會影響彼此的敏感度;(4)土體容重的降低會使黏聚力敏感度有較大程度的增加。可以推論，在容重低于一定值時，對邊坡穩定系數影響的主導因素會發生變化。

綜上所述，對邊坡穩定性帶來的影響即敏感度而言，內摩擦角>黏聚力>土體容重，然而，土體容重盡管對穩定系數的影響相對較小，卻會較大程度地改變邊坡穩定性對黏聚力的敏感度。這一點具有現實意義，隨著土層深度的增加，在重力作用下容重也會發生改變，隨之改變邊坡穩定系數對不同參數的敏感度。針對不同層土體，對邊坡治理過程中要注意分析影響穩定性的主導因素，針對性治理。