GLC 硅質輕型墻板抗彎性能試驗研究
王松巖劉學光焦 紅馬海程陳茂輝
(1.山東建筑大學 土木工程學院,山東 濟南250101;2.漢宸國際工程設計集團有限公司,山東 濟南250101)
0 引言
近年來,隨著節能環保要求的不斷提高和勞動力成本的不斷增加,國家和各省市都提出了建筑裝配化要求,為裝配式建筑帶來了難得的發展機遇[1],三板(樓板、外墻板、內墻板)的需求量大大增加。 但是,在各類裝配式墻板層出不窮的前景下,也存在著各種各樣的問題需要去關注和解決。 產品的標準化、規模化及施工的專業化均需提升,各項性能需要通過工程應用實踐進行驗證[2]。 研究集節能、環保于一身的新型復合夾芯板,對于裝配式建筑的發展具有重要意義。 針對以上國家裝配式建筑發展策略和現行建筑墻板存在的種種問題,GLC 硅質輕型墻板(以下簡稱GLC 墻板)是一種能夠滿足各種建筑結構形式需求,更加符合裝配式建筑和節能、環保要求的新型建筑材料產品。
目前,學者們對于新型復合夾芯板的研究主要集中在不同種類的面層和芯材進行組合方面。 面層材料主要分為金屬面層[3-7]和非金屬面層[8-11],芯材可以分為有機材料[12-13]和無機材料[14]。 在試驗研究方面,BENAYOUNE 等[15]、侯和濤等[16]、馮智勇等[17]對鋼絲桁架復合墻板進行了抗彎試驗,結果表明兩側混凝土面層在鋼絲桁架的連接下組合作用明顯,試件的組合程度與抗剪連接件的剛度呈正比關系。 MUGAHED 等[18]、張國偉等[19]、馮琳[20]對不同夾芯材料的復合夾芯板進行試驗研究,忽略芯材的抗彎剛度,得出相應的開裂承載力計算公式。 蘇幼坡等[21]介紹了無共同作用、完全共同作用和部分共同作用3 種混凝土夾芯板的內力與變形問題,并推導出計算公式。
綜上所述,目前國內外對新型復合夾芯板的研究成果主要集中在鋼絲桁架作為連接件忽略芯材彎曲剛度,求解墻板承載力計算方面。 GLC 墻板的芯材是GLC 墻板的主要組成部分,耐堿玻纖網是墻板增強材料,其為墻板變形和承載力的主要影響因素,因此有必要對GLC 墻板的抗彎性能進行深入研究,提出適用于GLC 墻板特點的抗彎承載力計算方法,為該墻板在工程中的設計與應用提供參考。
1 試驗概況
1.1 試件設計
GLC 墻板是由發泡水泥芯材、砂漿層以及砂漿層內的耐堿玻纖網3 種不同的材料復合成型的輕質板材。 其中,發泡水泥芯材是以硅為主要原材料,采用晶型轉變增強技術通過化學發泡制成,主要起支撐作用,增大了結構的厚度,從而提高截面慣性矩。發泡水泥芯材兩側為專用水泥砂漿,砂漿層內耐堿玻纖網的型號為ARNP5×5-100L(160)[22],面層砂漿采用雙層玻纖網,中間層砂漿采用單層玻纖網。GLC 墻板共有兩種復合形式,即單層芯材復合形式普通型(Common Wallboard,CW 型)和多層芯材復合形式加強型(Reinforced Wallboard,RW 型)。 為達到抗風、抗震和保溫的要求,一般使用180 和200 mm的墻板厚度。 試驗一共設計了5 組方案,進行15 個試件的抗彎試驗,試件具體設計參數詳見表1。 GLC 墻板類型如圖1 所示。
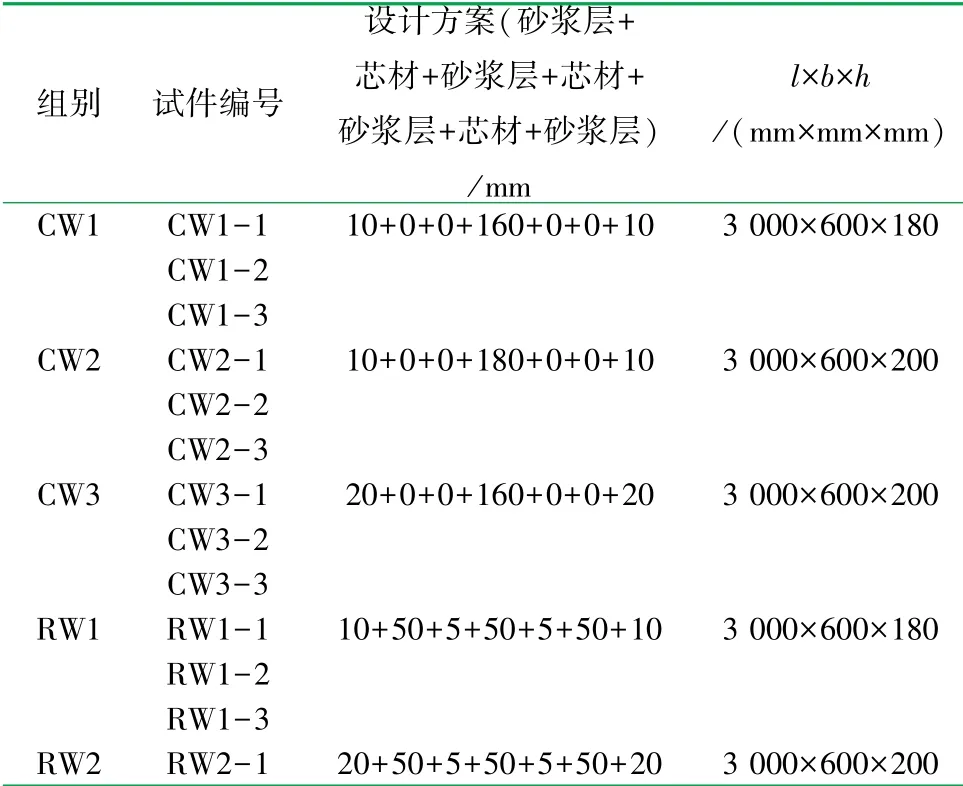
表1 GLC 墻板試件基本參數表
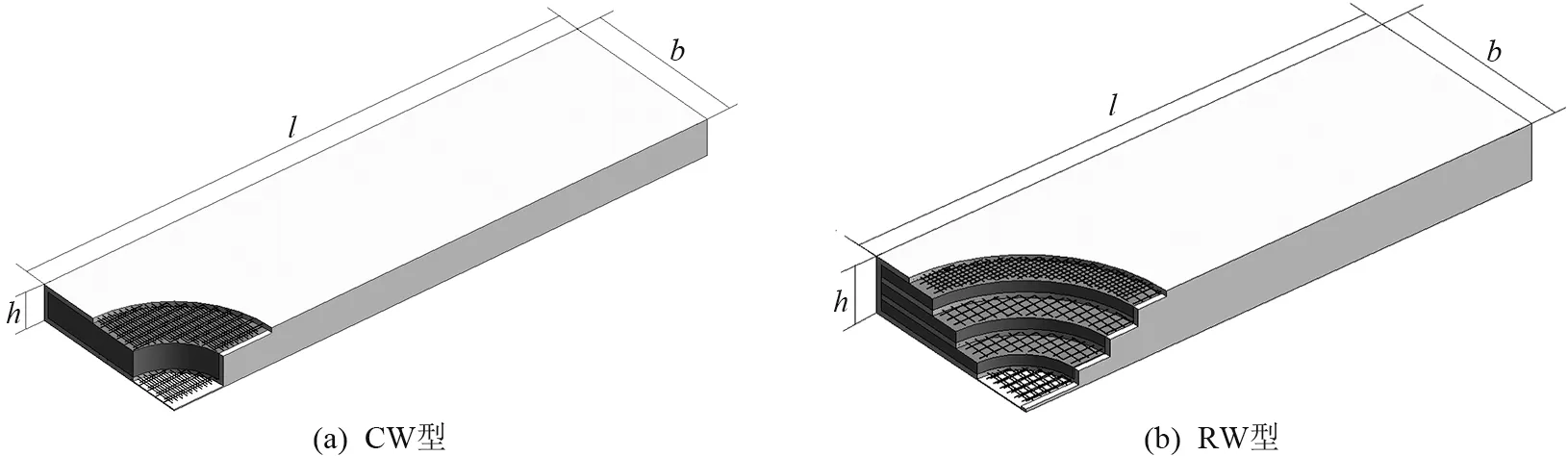
圖1 GLC 墻板類型示意圖
1.2 材性試驗
澆筑標準材性試塊,和試件在相同環境下養護。試驗測得發泡水泥芯材、砂漿層以及耐堿玻纖網各項力學性能指標見表2。 其中,試驗測得發泡水泥芯材極限壓應變為0.002 7、砂漿極限壓應變為0.001 6、耐堿玻纖網極限拉應變為0.03。
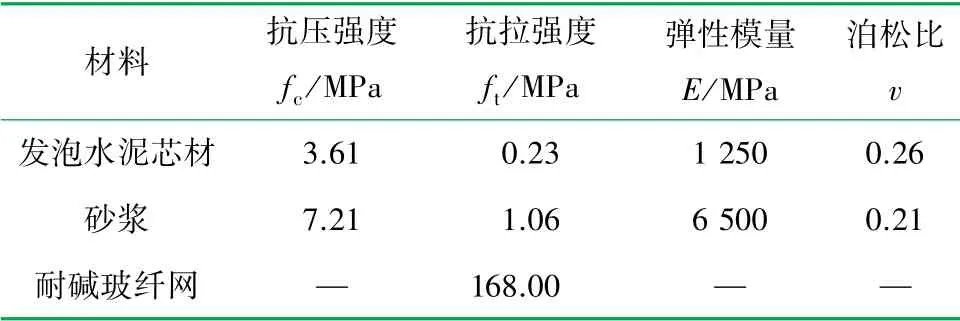
表2 所需材料基本力學性能表
1.3 試驗裝置及測點布置
根據GB 15762—2008《蒸壓加氣混凝土板》[23]制定試驗裝置及測點布置如圖2 所示,位移計和應變片讀數采用TST3826E 動態應變測量系統進行數據采集。
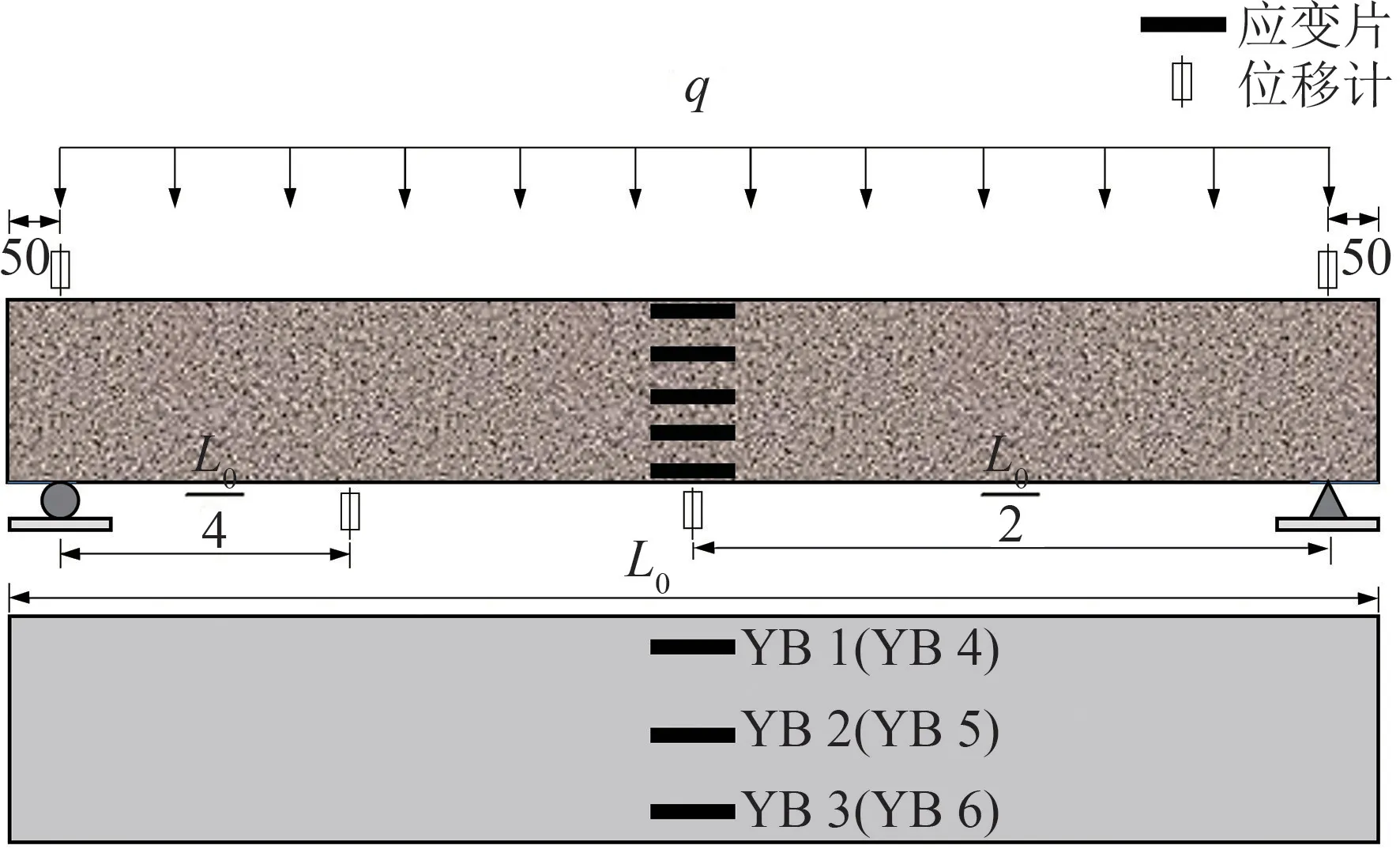
圖2 試驗裝置和測點布置示意圖/mm
1.4 加載制度
根據GB 15762—2008 的規定,通過紅磚滿鋪在試件表面來模擬均布荷載的方式,測定GLC 墻板的抗彎性能。 計算所得到的短期撓度檢驗階段荷載分為5 級,每級荷載為83 kg;出廠檢驗階段荷載分為3 級,每級荷載為29 kg;最后進入承載力檢驗階段,每級荷載為41.5 kg,直至墻板破壞。 規定每級荷載質量誤差≤0.2 kg,荷載加載完畢后靜置5 ~10 min或待數據采集系統讀數穩定后進行下一級加載,期間觀察并記錄試驗現象。 加載曲線如圖3 所示。
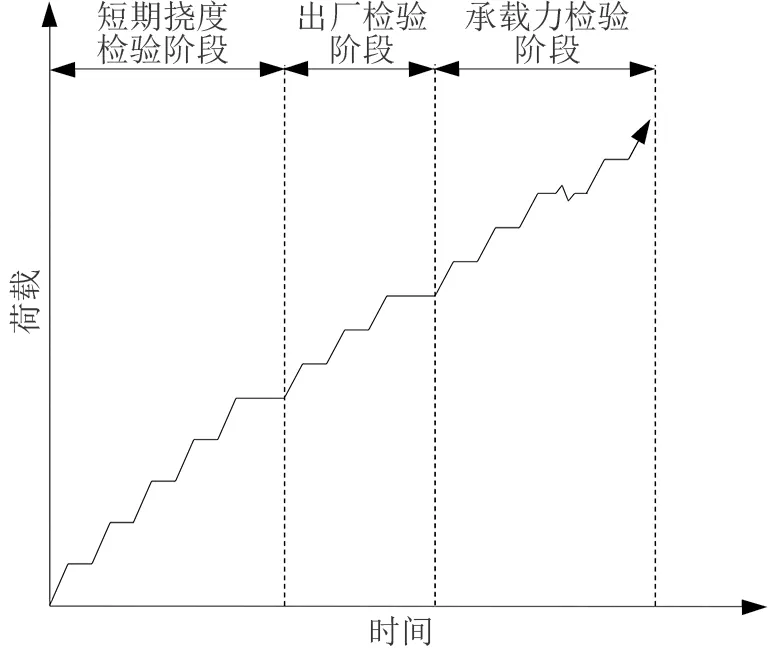
圖3 加載曲線示意圖
2 試驗現象與結果
在試驗過程中,CW 型試件與RW 試件破壞各有特點,采用數理統計的方法,分析篩選兩種類型試驗數據及現象,取其中具有代表性的試件進行描述。
CW2-1 試件自重下初始撓度為零;當荷載加至3.32 kN(1.91 kN/m2)時,在板材跨中附近出現首條裂縫,方向豎直向上,此時跨中撓度為1.10 mm;當荷載加至4.15 kN(2.39 kN/m2)時,板底出現貫通裂縫并伴有新的細微裂縫產生;當荷載加至7.10 kN(4.08 kN/m2)時跨中撓度達到l0/200;隨著荷載的繼續增加,裂縫主要集中在板長的l0/4 ~3l0/4 區域內,試件出現明顯的彎曲撓度。 繼續加載至13.32 kN(7.65 kN/m2)時板材突然破壞,表現為底部耐堿玻纖網斷裂,頂面砂漿層無明顯壓潰現象,類似于鋼筋混凝土梁的少筋破壞。
RW1-2 試件自重下初始撓度為零;當荷載加至3.32 kN(1.91 kN/m2)時,跨中附近出現豎直向上的首條裂縫,此時跨中撓度為1.32 mm;當荷載加至9.59 kN(5.51 kN/m2)時,裂縫主要集中于跨中左、右350 mm 以內,多為豎直裂縫,此時跨中撓度達到l0/200;隨著荷載的繼續增加, 原有裂縫長度>3/4 截面,寬度激增并發展為斜裂縫,此時下砂漿面層開始出現與墻板主體剝離的裂縫;當荷載加至14.98 kN(8.61 kN/m2)時,跨中撓度達到63.14 mm,認為試件達到極限承載能力狀態;繼續加載至16.23 kN(9.32 kN/m2)時板材突然破壞,表現為下砂漿面層內耐堿玻纖網斷裂,頂面砂漿層無明顯壓潰現象。 5 組GLC 墻板的試驗結果見表3。
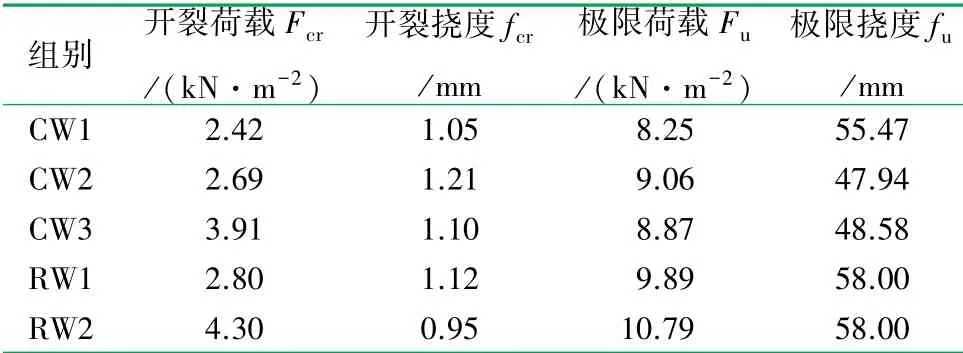
表3 墻板試件加載結果表(平均值)
從以上試驗現象描述中可以得到GLC 墻板在均布荷載作用下主要存在兩種破壞形態:(1) 彎曲破壞 發生在CW 型試件。 破壞時跨中撓度明顯,下面層砂漿內玻纖網被拉斷,芯材斷裂,上面層砂漿無明顯壓潰現象。 (2) 彎剪破壞 發生在RW 型試件。剪切面主要發生在砂漿層和芯材的粘結處,破壞時跨中撓度>l0/50,底部砂漿面層內玻纖網被拉斷,頂面砂漿層沒有明顯的壓潰現象。 GLC 墻板破壞形態如圖4 所示。

圖4 GLC 墻板破壞形態圖
3 試驗分析
3.1 墻板荷載-跨中撓度曲線分析
根據試件加載數據繪制的荷載-跨中撓度曲線是GLC 墻板抗彎性能的綜合體現,也是進行GLC墻板受力性能分析的重要依據。 兩種復合形式試件的荷載-跨中撓度曲線如圖5 所示,荷載-跨中撓度曲線可以分為雙線型彎曲破壞和三線型彎剪破壞兩種不同型號試件。 其荷載-撓度曲線如圖6 所示。
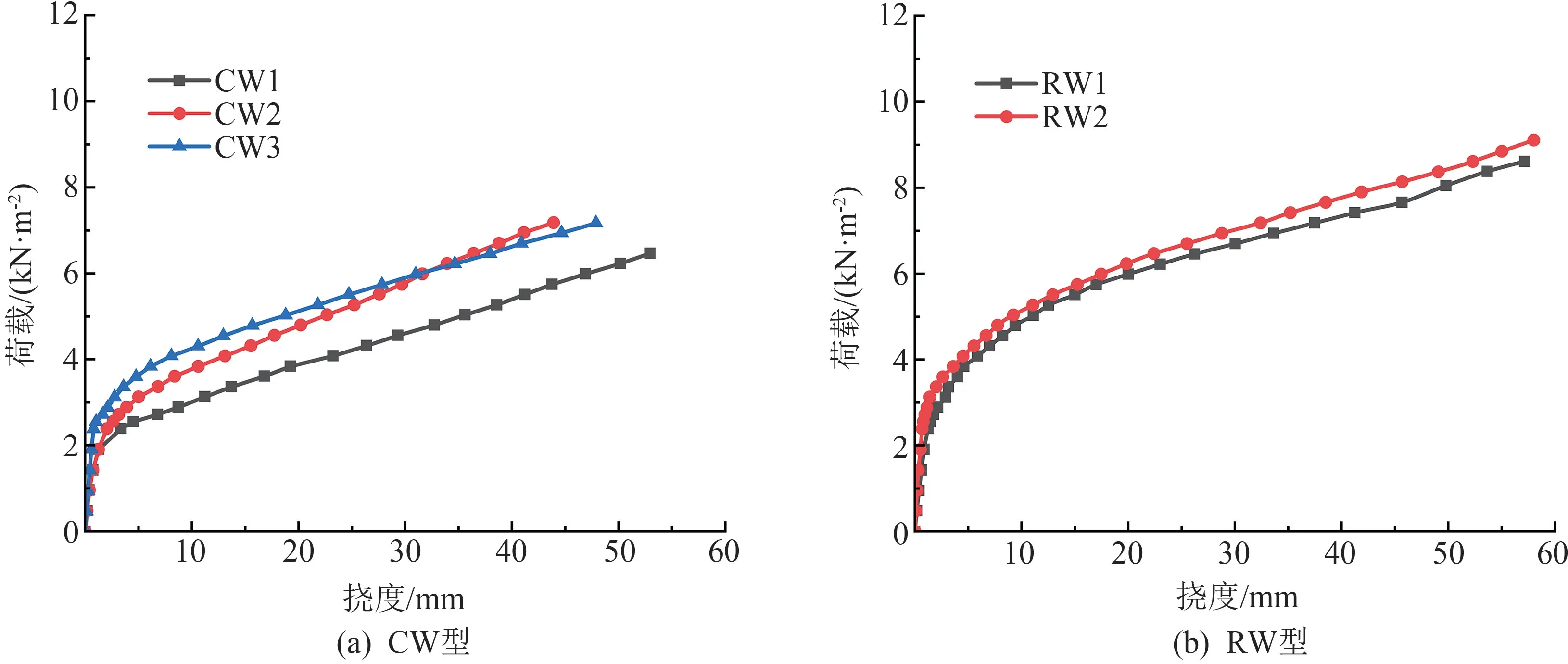
圖5 荷載-跨中撓度曲線圖
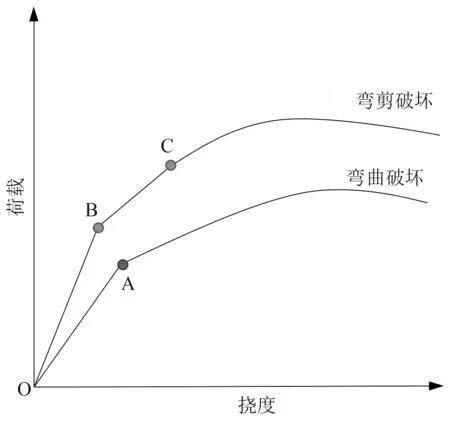
圖6 典型荷載-撓度曲線圖
彎曲破壞依據不同的斜率可將曲線分為兩個階段。 第一階段的彈性階段在試件加載初期,OA 段荷載與跨中撓度呈正比增長,受拉砂漿面層尚未開裂,此時墻板應力應變水平較低;隨著荷載的增加進入第二階段:當試件達到抗裂強度極限后,裂縫的出現削弱了墻板剛度。 開裂后截面曲率和跨中撓度增長變快,荷載-撓度曲線的斜率變小,最終破壞形態如圖4(a)所示。
彎剪破壞可以分為3 個階段:第一階段同彎曲破壞第一階段;第二階段為BC 段,帶裂縫工作的彈性階段,受拉區砂漿層出現裂縫,彈性剛度較初始剛度有一定程度上的下降。 隨著荷載增加,裂縫數量增多并伴隨著斜裂縫的初現;第三階段為非線性工作階段,隨著荷載的繼續增加斜裂縫寬度迅速發展,斜裂縫穿過半個截面,截面曲率和跨中撓度顯著增加,最終破壞形態如圖4(b)所示。
3.2 墻板荷載-應變曲線分析
由于試件在開裂后,個別裂縫穿過砂漿面層的應變片,導致應變片破壞而提前退出工作,因此只分析開裂荷載之前的砂漿面層應變數據,5 組試件荷載-應變曲線極為相似,以RW1-2 試件為例得到荷載-應變曲線。 如圖7 所示,試件開裂之前,砂漿面層應變均隨著荷載的增長趨勢表現為線性增加。 各組試件拉、壓應變基本對稱,這表明試件兩側的砂漿面層的應變變形基本協調,截面的中和軸穩定在試件截面中間。 試件整體展現出穩定的完全組合工作狀態。 這樣組合工作狀態,意味著采用開裂理論分析時,可以把試驗的GLC 墻板視為一個整體并進行計算。
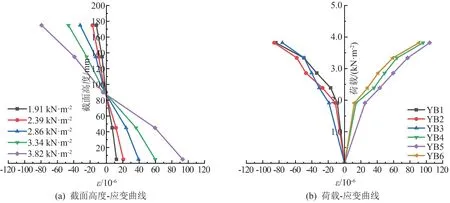
圖7 GLC 墻板荷載-應變曲線圖
3.3 墻板加載結果分析
根據表3 和圖8(a)分析可知:隨著砂漿層厚度的增加,開裂承載力成正比增長。 其中試件CW1、CW2 組研究了砂漿層厚度不變情況下芯材厚度由160 mm 增加到180 mm,開裂承載力提高了11.18%;根據表3 和圖8(b)分析可知:CW 型試件極限承載力相當;RW 型試件極限承載力相當;RW 型均優于CW 型;與CW1 相比,RW1 極限承載力約提高了20%;與CW3 相比,RW2 極限承載力均也約提高了20%。 通過以上分析可知:GLC 墻板的開裂承載力應同時考慮砂漿層和芯材的貢獻作用,砂漿層厚度的增加有效地提高了試件的初始剛度和試件的開裂承載力;極限承載力主要取決于墻板內受拉耐堿玻纖網的抗拉強度。 多層復合形式的GLC 墻板,沒有充分發揮耐堿玻纖網的抗拉強度,在板厚與最外側耐堿玻纖網的位置相同時,RW 型比CW 型試件的極限承載力僅提高了約20%。
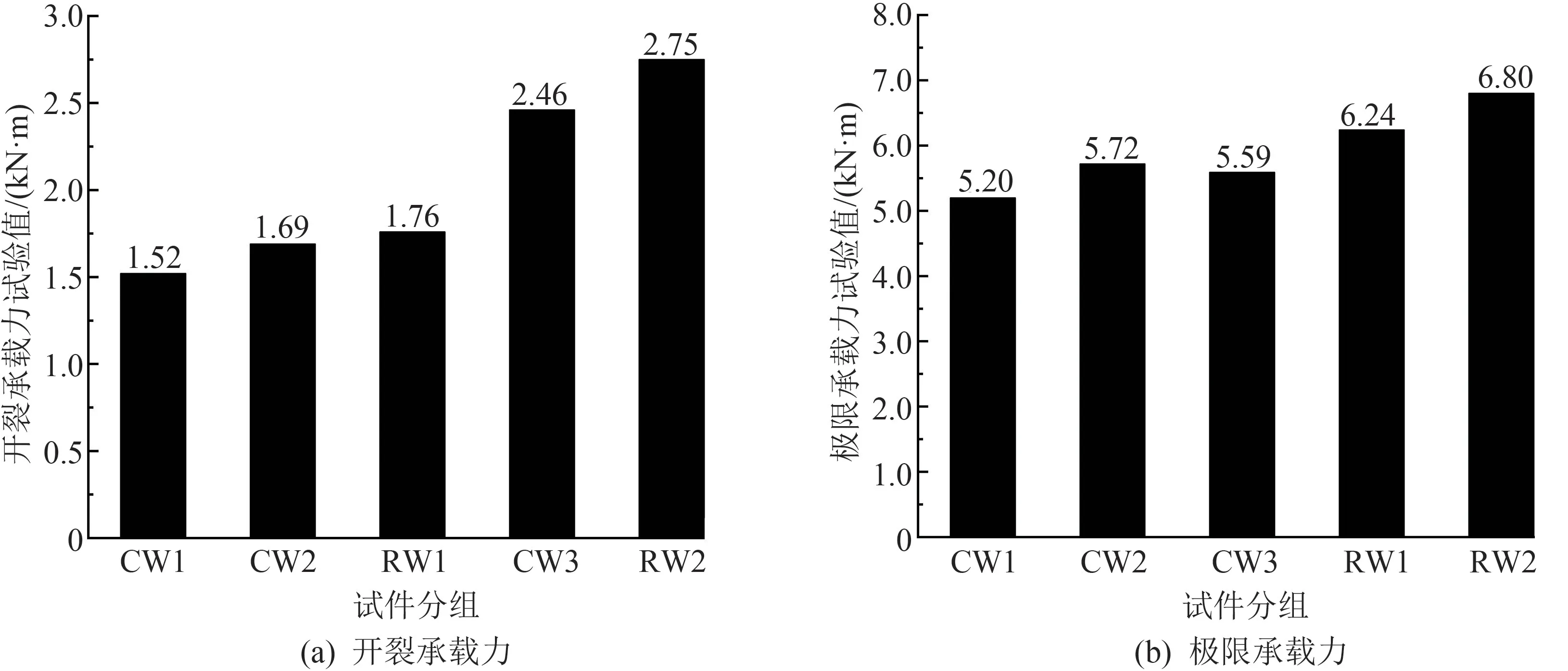
圖8 GLC 墻板承載力圖
4 GLC 墻板承載力計算
4.1 GLC 墻板開裂承載力計算
截面開裂承載力的計算做了如下假設:(1) 平截面假定;(2) 構件開裂前處于彈性狀態(試驗已驗證),可以采用材料力學的公式計算其應力和應變;(3) 取砂漿層的抗拉強度ft作為砂漿層的開裂極限應力;(4) 不考慮耐堿玻纖網對開裂承載力的貢獻作用。
根據假設(4),GLC 墻板開裂之前,視為由砂漿層和發泡水泥兩種材料組成的夾芯板,計算前,應將材料按照合力不變及應變相同的條件,并做了均質假定。 將發泡水泥芯材轉換為砂漿,得到換算后的截面面積Am=Ac/αE,其中Ac為發泡水泥的截面面積,m2;αE為砂漿彈性模量與發泡水泥彈性模量的比值。 為保證換算截面后中性軸位置不變,只改變發泡水泥的寬度不改變其高度,即換算后的截面寬度beq與原截面的有效寬度b之間的關系為beq=b/αE,計算模型如圖9 所示。
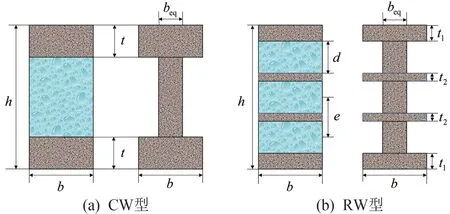
圖9 換算截面模型圖/mm
換算截面后的慣性矩ICW和IRW分別由式(1)和(2)表示為
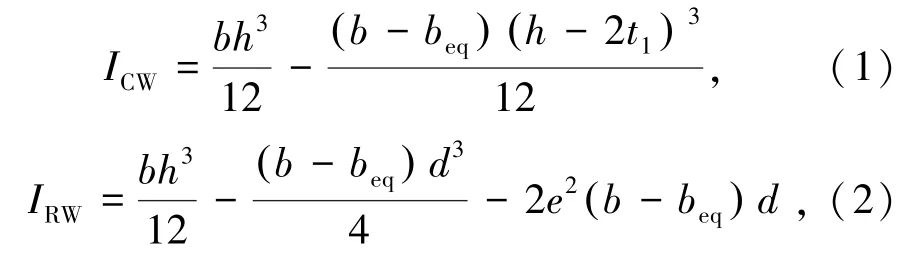
式中ICW為CW 型墻板換算截面的慣性矩,mm4;IRW為RW 型墻板換算截面的慣性矩,mm4;b為截面寬度,mm;h為截面高度,mm;t1為面層砂漿厚度,mm;t2為中間層砂漿厚度,mm;d為RW 型芯材的厚度,mm;e為RW 型芯材中線之間的距離,e=d+t2,mm。
當板底面層砂漿拉應力達到fmt時,認為墻板開裂,根據材料力學公式可將GLC 墻板的開裂承載力由式(3)表示為

式中Mcr為開裂承載力,kN·m;fmt為砂漿抗拉強度,MPa;I0為換算截面慣性矩,mm4;y0為換算截面的重心到截面下邊緣的距離,mm。
將表2 中材料的基本力學性能代入式(3)得到表4 開裂承載力理論值與試驗值對比表,結果表明二者吻合較好,誤差最大為13.06%。
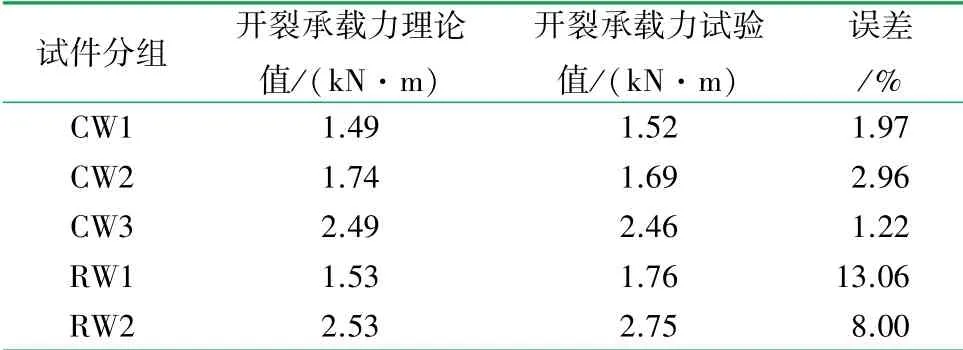
表4 開裂承載力試驗值與理論值對比表
4.2 GLC 墻板極限承載力計算
4.2.1 理論分析
GLC 硅質輕型墻板在開裂后,下部砂漿面層裂縫截面處發生了內力重分布,砂漿層將自己所承受的絕大部分拉力傳遞給玻纖網。 由于試件制作的特殊性無法測得試驗中玻纖網的實際應變數值,但是根據試驗現象以及試驗數據不難發現,板材在開裂后截面大致遵循平截面假定。 材性試驗測得耐堿玻纖網達到抗拉強度時的拉應變為εs=0.03,對于CW型試件來說板材破壞的標志是玻纖網被拉斷,頂面砂漿層應變約為1 100×10-6未達到其極限壓應變,沒有壓潰現象,可以判定砂漿處于彈性階段。 破壞前墻板應變趨勢如圖10 所示。
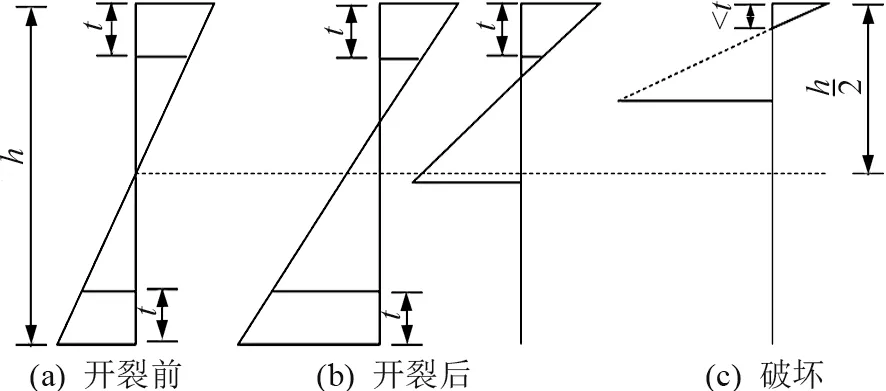
圖10 開裂后墻板應變變化趨勢圖
4.2.2 CW 型GLC 硅質輕型墻板極限承載力計算
由于耐堿玻纖網的拉伸變形較大,試件在破壞時中和軸上升至受壓區砂漿層內。 計算截面極限承載力做出如下假設:(1) 符合平截面假定;(2) 下部玻纖網,取其拉伸斷裂強度作為玻纖網的極限強度;(3) 忽略芯材的抗拉作用;(4) 忽略砂漿層的抗拉作用;(5) 忽略受壓區耐堿玻纖網的抗壓作用。
極限承載力計算模型如圖11 所示,由此可得到受壓砂漿應變εcm、受壓區砂漿合力Cm以及耐堿玻纖網合力Ts,分別由式(4)~(6)表示為
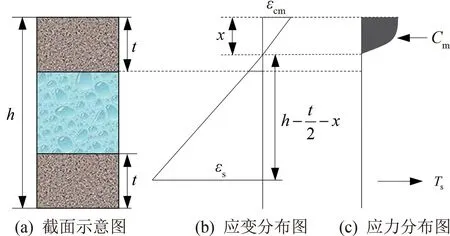
圖11 極限承載力計算模型圖
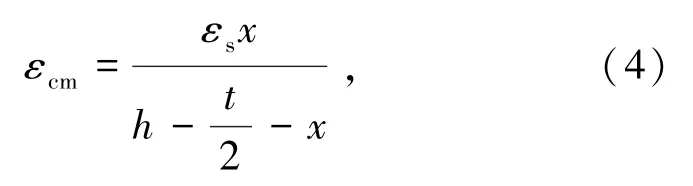
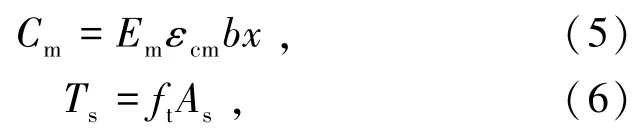
式中εcm為受壓砂漿應變;εs為玻纖網極限拉應變,取εs=0.03;x為受壓區高度,mm;t為面層砂漿厚度,mm;Cm為受壓區砂漿合力,kN;Em為砂漿的彈性模量,MPa;ft為耐堿玻纖網抗拉強度,MPa;As為耐堿玻纖網截面面積,取240 mm2。
根據合力平衡Ts=Cm推出中和軸位置x可由式(7)表示為

此時極限承載力Mu可由式(8)表示為
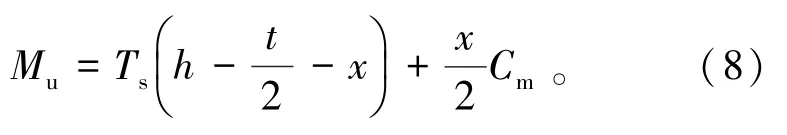
式中Mu為極限承載力,kN·m。
4.2.3 RW 型GLC 硅質輕型墻板極限承載力計算由于玻纖網以及試件制作的特殊性,無法得到其在抗彎過程中的真實應變,為了方便計算,根據3.3中的分析:同等厚度,最外側玻纖網位置相同條件下RW 型比CW 型極限承載力提高了20%。 可以近似的得到RW 型試件的極限承載力可由式(9)表示為

式中為CW 型GLC 墻板極限承載力,kN·m;為RW 型GLC 墻板極限承載力,kN·m。
按式(8)和(9)可得到極限承載力理論值與試驗值的對比,見表5。
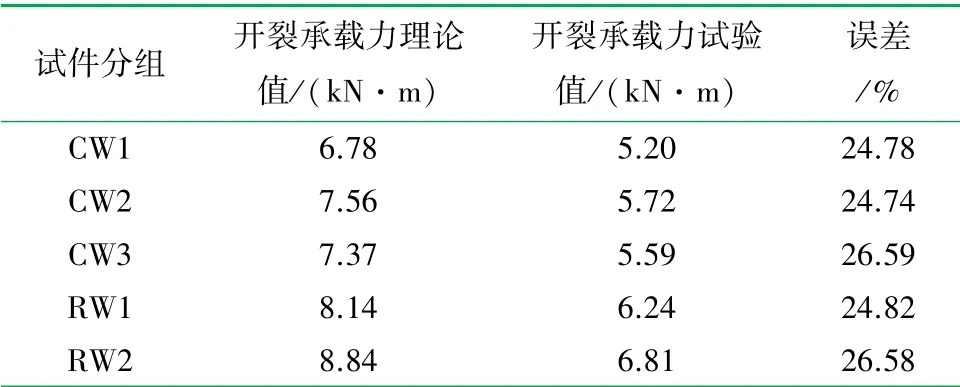
表5 極限承載力試驗值與理論值對比表
根據表5 所示極限承載力理論計算值與試驗值誤差較大,說明玻纖網在GLC 硅質輕型墻板中作為增強材料,兩層玻纖網對極限承載力的貢獻并不是簡單的疊加原理。 因此需要對其進行折減,通過簡單的誤差累計計算,可以得到一個折減系數0.75,此時根據平截面假定算得砂漿層應變值與試驗值、理論計算極限承載力與試驗值比較,吻合良好。 墻板在使用過程中考慮具有一定的安全儲備,安全系數取1.4,最后得到GLC 硅質輕型墻板極限承載力計算理論公式可由式(10)表示為
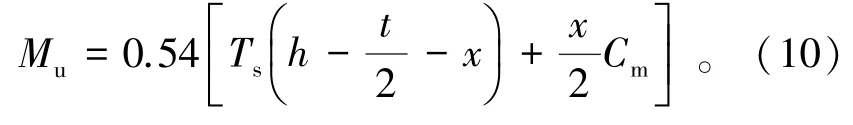
5 結論
通過5 組GLC 墻板的抗彎試驗,并在此基礎上展開理論分析,可以得到以下結論:
(1) 隨著砂漿層厚度的增加,試件的初始剛度和開裂承載力顯著提高;復合形式的改變,失效模式從彎曲破壞轉為彎剪破壞。 多層芯材復合形式加強型試件的開裂承載力與極限承載力均優于單層芯材復合形式普通型試件,說明多層復合形式的GLC 墻板能夠有效地抑制裂縫的產生和發展,提高試件的抗彎承載能力;
(2) 試件開裂前,剛度相對較大,撓度較小,復合材料之間處于完全組合狀態,墻板處于彈性工作階段,開裂承載力以強度控制比較合理;考慮發泡水泥芯材的抗彎剛度,通過等效理論得到開裂承載力計算公式,理論計算結果與試驗值吻合較好;
(3) 試件開裂后,彎曲撓度明顯,極限承載力主要取決于耐堿玻纖網的抗拉強度,根據經典抗彎理論得到極限承載力計算公式,理論值與試驗值相比具有較大的安全儲備。

