受電弓空氣彈簧的熱力學模型研究

劉久銳，周寧，姚永明，劉釗，張欣，張衛華

(西南交通大學 牽引動力國家重點實驗室，四川 成都 610031)

0 引言

電力牽引機車的受電弓作為列車上與接觸網進行耦合并由此獲得電能的關鍵設備，其能否安全、穩定地運行直接決定了列車的行車安全和質量。受電弓底座上的空氣彈簧發揮著緩沖和吸振的重要作用，其性能會直接關系到弓網動態接觸能否平穩、持續、可靠，并且也會對弓網動力學性能產生重大影響[1]。相比于針對列車轉向架上空氣彈簧的研究[2]，針對列車受電弓上空氣彈簧的研究相對較少，而專門針對其建模問題的研究更不多見。為此，有必要對此問題進行討論和研究。

國內外的學者對空氣彈簧早有青睞，并做了大量的研究[2-6]。文獻[2]建立了一種考慮彈性力、摩擦力和黏滯力的非線性空氣彈簧模型，在該模型中非線性部分主要是空氣彈簧自身橡膠材料的摩擦和氣動系統中的節流孔部分。文獻[4]研究了存在于列車二系懸掛中的空氣彈簧-導氣管路-氣箱氣動系統，將建立的模型整合到列車的多剛體模型中，并通過不斷地調整空氣彈簧、氣動管路、氣箱的模型再將其進行組合，從而得到了5個不同的模型。文獻[5]結合庫侖摩擦模型、分數導數模型和空氣彈簧有效面積以及有效容積的變化，得到了空氣彈簧的非線性模型，并給出該模型的參數識別方法。文獻[6]給出一種用來描述空氣彈簧-導氣管路-氣箱氣動系統的高精度熱力學模型，該模型不但考慮了氣動系統本身的熱力學特性，還分別考慮了來自空氣彈簧振動時產生的庫侖摩擦力和黏滯力。

在空氣彈簧的建模中，相比于更受關注的空氣彈簧垂向力F與振動幅值x之間比值F/x的頻響特性，空氣彈簧內部氣壓Pa與振動幅值x之間比值Pa/x的頻響特性更加簡單，其主要受到空氣彈簧及其附加氣動系統的熱力學特性的影響。同時，Pa/x模型的建立也是計算F/x模型的基礎。因此，建立一種能夠準確、可靠地描述受電弓空氣彈簧Pa/x的模型就顯得很有意義。

1 受電弓空氣彈簧試驗

1.1 試驗系統

圖1為此次測試中空氣彈簧及其附加氣動系統的結構示意簡圖，其中，空氣彈簧為受電弓上囊式空氣彈簧，其一端固結在壓力傳感器上，另一端與液壓作動器固結且液壓作動器僅表示為一個加載在空氣彈簧上端的輸入位移。空氣彈簧的上端由一根膠質管道連接，其另一端連接到帶手動控制閥門的氣動調壓閥內側，而氣動調壓閥的外側直接連到外源氣泵。在該系統中連接有兩個測壓計，一個被安置到空氣彈簧的上端蓋處以測量空氣彈簧內部的氣壓，另一個則在緊靠氣動調壓閥內側的位置以測量調壓閥內端的氣壓。壓力傳感器被安置在空氣彈簧下部與地面之間的位置以測量空氣彈簧在垂向上的受力；空氣彈簧的垂向位移由液壓作動器上自帶的拉線傳感器進行測量。以上3種類型共4個傳感器的輸出信號均被采集到上位機中。此上位機還能同時控制液壓作動器的加載方式，包括：位移大小、時間、位移形式、頻率等。試驗人員僅需要通過上位機和氣動調壓閥的手動旋鈕就可以完成對空氣彈簧及其附加氣動系統的控制，包括空氣彈簧的高度、內部氣壓的控制等。所采集的該氣動系統數據包括垂向力、位移、氣壓、振動頻率、波形等。

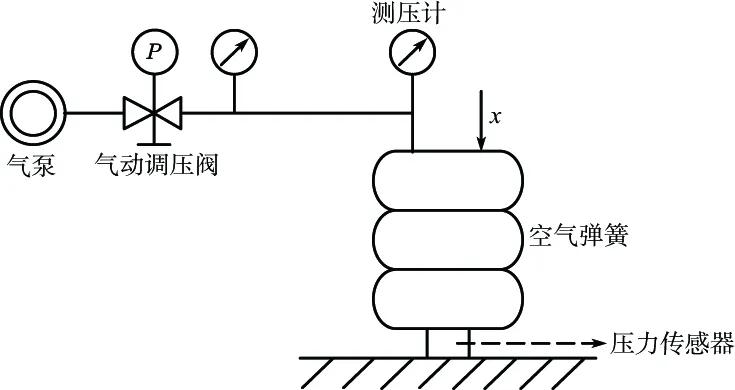
圖1 氣動系統的結構示意簡圖

1.2 試驗工況

試驗是在考慮空氣彈簧在實際使用過程中經常遇到的不同使用條件(如：不同的彈簧高度和內部氣壓等)以及不同工作條件(如：從低頻到高頻的工作頻率以及相應頻率下的振動幅值等)下而進行的，其具體數據如表1所示。

表1 試驗工況

2 空氣彈簧的熱力學建模

在對空氣彈簧自身的熱力學性能及行為進行描述時，使用多變過程方程、理想氣體狀態方程以及質量流量方程描述[7]如下：

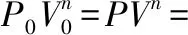
(1)

(2)

(3)

以上式(1)為多變過程方程；式(2)為理想氣體狀態方程；式(3)為質量流量方程。式中：P、V、n分別代表氣壓、體積以及多變指數；n′、R、T、m、M、Ra分別代表物質的量、通用氣體常數、溫度、質量、摩爾質量以及干空氣的理想氣體常數；G、t、ρ、h則分別代表質量流量、時間、流體密度以及空氣彈簧的工作高度。

現在對式(1)進行如下變換：

(4)

式中K′、K均為任意給定的常數。

同時，對式(4)進行如下的變換并對其變換后的結果聯立，可得

(5)

將式(5)代入到式(3)中并將其變換后所得到的結果與式(2)進行聯立，可得

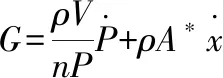
(6)

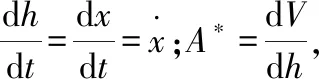
同時，觀察式(1)、式(2)、式(4)和式(5)可知，這些公式并沒有限定為只能用于空氣彈簧建模的推導，而直到將它們與式(3)聯立進而推導得到的式(6)才是用來表述空氣彈簧內部質量流量與氣壓、位移之間關系的公式。

假定氣動系統內部的空氣質量流量在管道中可以表示為G*，且假定該氣動系統中并沒有發生內外氣體交換的情況，而由于氣動調壓閥為膜式調壓閥，故在其輸出端口，即該閥與氣動系統管道連接的端口部分，如果出現了比較大的氣壓波動，那么就可能會導致閥口打開，使得閥門內外的氣體發生物質交換。根據連續性定理，有

G=G*

(7)

同時，已知管道內部的氣體會與空氣彈簧內部的氣體在中低頻下發生物質交換，則它們之間在客觀上必定存在一個物質交換規律，盡管這種規律并不一定能夠以一個比較簡單、高效的公式表達出來，但是出于簡化物理模型的目的，現在將這種物質交換規律假定成一個由氣動調壓閥內部端口氣壓Pv、空氣彈簧內部的氣動壓力Pa以及一個未知的阻值RF決定，并最終表述為質量流量G*的方程：

(8)

式中P0、ΔPv、ΔPa分別是空氣彈簧內處于平衡時的靜態壓力值、氣動調壓閥的動態變化值以及空氣彈簧內部氣壓的動態變化值。

將式(8)和式(7)代入到式(6)中，可得

(9)

而在式(9)中，對于(P0+ΔPa)和(x0+Δx)這兩部分的求導，考慮到P0和x0均為常數，則應該視為對ΔPa和Δx的求導，化簡之后有

(10)

現在對式(10)進行拉普拉斯變換，有

(11)

通過上述的一系列假設和變換，得到了一個用來描述在復數域s平面內氣動調壓閥的氣壓動態變化值ΔPv(s)與空氣彈簧內部的氣壓動態變化值ΔPa(s)以及空氣彈簧垂向位移的動態變化值Δx(s)之間對應關系的式(11)。而空氣彈簧內部的氣壓動態變化值ΔPa(s)與空氣彈簧垂向位移的動態變化值Δx(s)在復數域s平面內的關系可看作是該系統的輸出傳遞函數，則有如下控制方程：

(12)

式中：ΔPref為參考氣壓的變化值，該氣壓由氣動調壓閥內外兩端的氣壓值決定；τ為人為設定的某個未知的延遲。

式(12)是一個類似于慣性環節的控制方程，將式(12)代入到式(11)中，則有

(13)

根據文獻[8]，假定ΔPref=0，則有

(14)

觀察式(14)，結合實際的空氣彈簧工作環境，可知壓強、溫度等參數都不是定值。但為簡化模型，現根據實測數據有n、Ra、T0分別為1.12、287.058 J/(mol·K)、293 K，而A*、V0在空氣彈簧為140mm和170mm高度下分別為0.041 8m2、0.004 2m3和0.038 2m2、0.005 0m3，而P0在工作氣壓為0.30 MPa和0.45 MPa時，分別有4.0×105Pa和5.5×105Pa，假定RF和τ均為待定常數，則有最終模型

(15)

3 仿真結果與試驗數據對比

采用式(15)來描述空氣彈簧ΔPa(s)/Δx(s)的幅頻特性和相頻特性的仿真結果與實際數據的對比如圖2所示。

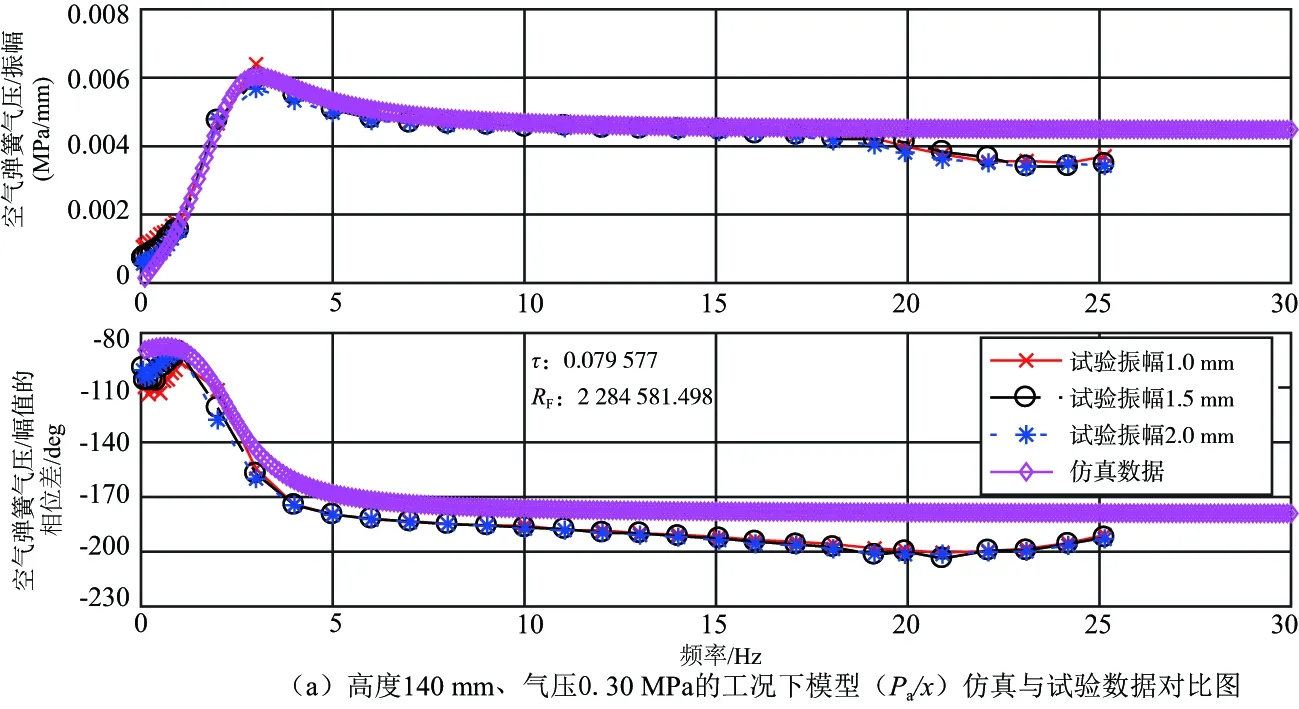
圖2 在不同氣壓及不同高度的工況下模型(Pa/x)仿真與試驗數據對比圖

結果分析：如圖2(a)-圖2(d)所示，用來描述受電弓空氣彈簧Pa/x的仿真模型，無論是在不同的空氣彈簧高度、內部氣壓還是振動幅值下，其仿真結果的幅頻特性曲線和相頻特性曲線在整體上都能與對應的試驗數據相吻合。雖然在極低頻段(0.05Hz～1.00Hz)和高頻段(18Hz～25Hz)上模型的仿真結果與試驗數據仍有一定的差異，但考慮到連接空氣彈簧與外界的氣動閥是一種膜式氣動閥，其本身在低頻段下有著一定的非線性特性，如：閥門兩側的瞬時氣壓差達到一定程度時會導致閥門部分打開從而使得內外物質發生交換，但這種影響不大且頻率范圍不廣，不會影響該模型在工程上的使用。而考慮到受電弓上空氣彈簧的實際工作環境，來自于弓網耦合時的較高頻振動會在傳導到空氣彈簧的過程中被路徑上的弓頭懸掛、上框架吸收掉[9]，同時在高頻下導氣管及其外面的氣動系統會被隔離出去，不參與氣體的物質交換，在此時僅有空氣彈簧內部的氣體會參與振動。因此，這種高頻下的差異不會對該模型在工程上的使用產生太大的影響。

4 結語

本文針對受電弓空氣彈簧內部氣壓與振動幅值之間比值Pa/x的幅頻和相頻特性，給出了一種相應的模型。從實際效果上來看，該模型不但結構較為簡單且總體效果較好，還能夠適用于多種不同的工況。最終得到了一種描述空氣彈簧Pa/x的準確、可靠的模型。