基于艾賓浩斯遺忘曲線的高中數(shù)學(xué)教學(xué)優(yōu)化探索

何利軍

（甘肅省靈臺(tái)縣第一中學(xué)，甘肅 靈臺(tái)）

新高考制度的推行從人才選拔角度“推翻”了原有應(yīng)試教育的育人理念，推動(dòng)了素質(zhì)教育在高中階段的深入發(fā)展。從新高考的數(shù)學(xué)題型中不難看出其對(duì)學(xué)生數(shù)學(xué)思維、綜合能力與創(chuàng)新素養(yǎng)的重視，作為高中數(shù)學(xué)教學(xué)的風(fēng)向標(biāo)，其也對(duì)高中數(shù)學(xué)的育人模式產(chǎn)生了深遠(yuǎn)的影響。在新高考的背景下，高中數(shù)學(xué)教學(xué)不僅強(qiáng)調(diào)以人為本原則，還很重視教學(xué)的科學(xué)性，如學(xué)生對(duì)概念、公式靈活應(yīng)用的前提是對(duì)基礎(chǔ)知識(shí)的系統(tǒng)掌握，但學(xué)生對(duì)過往知識(shí)的記憶和遺忘都是有規(guī)律的，如果教師不能引起重視并遵循規(guī)律開展教學(xué)，學(xué)生的數(shù)學(xué)學(xué)習(xí)很可能會(huì)出現(xiàn)漏洞[1]。從這一點(diǎn)出發(fā)，教師應(yīng)基于艾賓浩斯遺忘曲線加強(qiáng)對(duì)現(xiàn)有教學(xué)節(jié)奏的調(diào)整，以讓學(xué)生更好地整合新舊知識(shí)，有效應(yīng)對(duì)高考多變的題型考查。

一、艾賓浩斯遺忘曲線

人們?cè)谏钪蟹e累經(jīng)驗(yàn)，通常都能對(duì)這樣的現(xiàn)象達(dá)成共識(shí)，那就是逐漸忘記以往發(fā)生的事情，有時(shí)是昨天剛剛學(xué)習(xí)的單詞、有的時(shí)候是之前記憶的公式，在需要用的時(shí)候常常會(huì)“提筆忘字”，進(jìn)而影響對(duì)新知識(shí)的接受。實(shí)際上，這類遺忘的現(xiàn)象并不偶然，反而很常見，就像不論學(xué)生對(duì)課堂教學(xué)的印象多么深刻，兩周甚至是一個(gè)月后曾經(jīng)那些清晰的記憶就會(huì)逐漸變得模糊，乃至于后來的全然忘記，這就是著名的艾賓浩斯遺忘曲線的規(guī)律反映[2]。艾賓浩斯遺忘曲線（如圖1 所示）是德國(guó)心理學(xué)家艾賓浩斯的重要發(fā)現(xiàn)，它總結(jié)了人類遺忘的規(guī)律，并提出遺忘會(huì)隨著時(shí)間推移而在不同階段呈現(xiàn)出不同的變化，如記憶初期人們的遺忘速度通常很快，但到后來就會(huì)逐漸減慢。如將這一遺忘曲線應(yīng)用于學(xué)科教學(xué)中，將會(huì)幫助教學(xué)人員或?qū)W習(xí)者建立科學(xué)的記憶方法，以確保其對(duì)已學(xué)知識(shí)的靈活掌握。

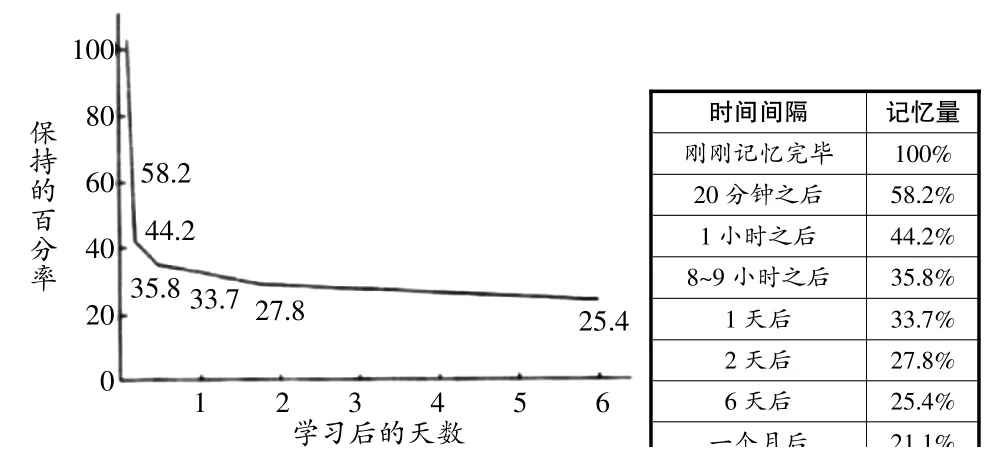
圖1 艾賓浩斯遺忘曲線

二、高中數(shù)學(xué)教學(xué)問題

（一）知識(shí)點(diǎn)抽象、分散，不易系統(tǒng)記憶

高中數(shù)學(xué)作為理工科目中的主要學(xué)科，具有知識(shí)量多，知識(shí)點(diǎn)覆蓋廣泛，概念、公式抽象度高的特點(diǎn)，不利于學(xué)生的理解、吸收和記憶，有時(shí)即便學(xué)生反復(fù)書寫、練習(xí)形成機(jī)械記憶，也容易在應(yīng)用時(shí)忘記。對(duì)此，教師往往認(rèn)識(shí)不到問題的癥結(jié)所在，會(huì)通過增強(qiáng)學(xué)生的習(xí)題訓(xùn)練強(qiáng)度來迫使其不斷將遺忘的內(nèi)容拾起，這不僅讓學(xué)生倍感疲憊，有時(shí)還會(huì)增加學(xué)生的心理壓力。高中數(shù)學(xué)知識(shí)點(diǎn)繁多、內(nèi)容抽象是事實(shí)，即便從學(xué)生學(xué)情的角度出發(fā)分析，也不能得出學(xué)生不會(huì)遺忘的結(jié)論。要讓學(xué)生達(dá)到鞏固所學(xué)知識(shí)的目的，教師還要根據(jù)科學(xué)理論從加強(qiáng)課堂復(fù)習(xí)、記憶的內(nèi)容著手，通過對(duì)學(xué)生記憶的不斷強(qiáng)化，減少其對(duì)過往接受知識(shí)的丟失。艾賓浩斯遺忘曲線可為高中數(shù)學(xué)教學(xué)提供一定的理論知識(shí)，教師完全可以通過對(duì)相關(guān)知識(shí)的梳理，重設(shè)課堂教學(xué)方案，將復(fù)習(xí)內(nèi)容納入其中，并采取多元形式幫助學(xué)生鞏固記憶，進(jìn)而提升學(xué)生對(duì)有關(guān)概念、公式的靈活運(yùn)用能力。

（二）學(xué)生學(xué)習(xí)主動(dòng)性差，知識(shí)保存率低

高中學(xué)生對(duì)數(shù)學(xué)的學(xué)習(xí)主動(dòng)性差，主要由以下兩點(diǎn)原因造成。一是高中數(shù)學(xué)知識(shí)繁多、相互之間聯(lián)系緊密，且抽象度高，不利于學(xué)生形成系統(tǒng)記憶，妨礙學(xué)生學(xué)習(xí)興趣的激發(fā)。正如上文提到的，學(xué)生理解、記憶大量知識(shí)點(diǎn)往往會(huì)失去對(duì)知識(shí)點(diǎn)深入探究的興趣，體現(xiàn)在學(xué)習(xí)過程中，就是學(xué)生的學(xué)習(xí)主動(dòng)性差，對(duì)知識(shí)的保存率低。另一個(gè)原因也是高中數(shù)學(xué)知識(shí)點(diǎn)多、難度大所致，學(xué)生自主探索往往會(huì)耗費(fèi)許多教學(xué)時(shí)間，教師為保證教學(xué)效率，大多數(shù)時(shí)候都由其主導(dǎo)學(xué)生學(xué)習(xí)，學(xué)生學(xué)習(xí)被動(dòng)，對(duì)知識(shí)的保存也缺少相應(yīng)的應(yīng)對(duì)機(jī)制，自然造成了其對(duì)已學(xué)知識(shí)點(diǎn)把握不足的情況。對(duì)此，教師要從以人為本角度著手重新設(shè)計(jì)高中教學(xué)方案，并積極尋找科學(xué)理論的支持，以為提升學(xué)生知識(shí)保存率提供有效的保障[3]。如在艾賓浩斯遺忘曲線中提取規(guī)律，能為高中數(shù)學(xué)的科學(xué)教學(xué)提供參考。

三、艾賓浩斯遺忘曲線在優(yōu)化高中數(shù)學(xué)教學(xué)中的應(yīng)用策略

（一）及時(shí)復(fù)習(xí)，結(jié)合定期復(fù)習(xí)

從艾賓浩斯遺忘曲線的規(guī)律中我們發(fā)現(xiàn)，人接觸新知識(shí)之后就會(huì)立刻開啟遺忘模式，而相關(guān)知識(shí)會(huì)遵循先快后慢的規(guī)律在人腦中停留，直到完全消失。而我們要想保持這段記憶的內(nèi)容，就需要根據(jù)這一規(guī)律采取相應(yīng)的干預(yù)措施，在人進(jìn)入遺忘階段時(shí)不斷加強(qiáng)鞏固記憶。尤其在高中數(shù)學(xué)教學(xué)中，復(fù)習(xí)是學(xué)生接觸新知識(shí)一段時(shí)間后必須采取的強(qiáng)化措施，根據(jù)艾賓浩斯遺忘曲線，教師要分兩階段對(duì)學(xué)生的記憶進(jìn)行及時(shí)的加強(qiáng)、鞏固，一是在學(xué)生剛學(xué)習(xí)新知識(shí)之后，二是定期地開展復(fù)習(xí)課程[4]。如筆者曾在“平面向量及其應(yīng)用”的教學(xué)中采取一課一復(fù)習(xí)、單元末整體復(fù)習(xí)的策略，在每次新知識(shí)的開啟前都先導(dǎo)入一段上節(jié)課學(xué)過的知識(shí)，目的就在于強(qiáng)調(diào)知識(shí)前后的銜接，幫助學(xué)生串聯(lián)知識(shí)，并鞏固其對(duì)此前知識(shí)的記憶。如此學(xué)生能在接觸向量的數(shù)乘時(shí)與前面學(xué)到的向量的加法相比較，不僅加強(qiáng)了學(xué)生對(duì)新知識(shí)的理解，還為學(xué)生對(duì)舊知識(shí)的深化認(rèn)識(shí)提供了途徑。

（二）知識(shí)整理，配合隨時(shí)回憶

在高中數(shù)學(xué)課堂上開啟復(fù)習(xí)課，除了要對(duì)以往學(xué)習(xí)的知識(shí)點(diǎn)進(jìn)行歸納總結(jié)，也要注意在習(xí)題訓(xùn)練中強(qiáng)調(diào)以往知識(shí)的運(yùn)用，如此學(xué)生才能整體把握新舊知識(shí)。因?yàn)閺?fù)習(xí)課不是圍繞新知識(shí)的學(xué)習(xí)，學(xué)生對(duì)復(fù)習(xí)資料都有一個(gè)基本的了解，此時(shí)基于艾賓浩斯遺忘曲線規(guī)律，可鍛煉學(xué)生對(duì)復(fù)習(xí)資料展開隨時(shí)記憶，讓學(xué)生通過重新讀取學(xué)過的知識(shí)不斷喚醒記憶，進(jìn)而對(duì)其已有的記憶進(jìn)行加強(qiáng)。作為一種積極主動(dòng)的復(fù)習(xí)方式，隨時(shí)地整理記憶可以與數(shù)學(xué)的習(xí)題訓(xùn)練做很好的融合，讓學(xué)生在習(xí)題訓(xùn)練中不斷挖掘之前的記憶，運(yùn)用此前學(xué)過的知識(shí)，從而促進(jìn)學(xué)生對(duì)知識(shí)點(diǎn)的鞏固。如筆者在“復(fù)數(shù)的幾何表示”復(fù)習(xí)課中就向?qū)W生導(dǎo)入了“求Z 的模和幅角：（1）z=-1+i，（2）z=i”這一問題，學(xué)生要解題就需要運(yùn)用到前面所學(xué)的復(fù)數(shù)的四則運(yùn)算知識(shí)，如此便推動(dòng)了學(xué)生對(duì)此前知識(shí)的自主復(fù)習(xí)，讓學(xué)生的解題過程變?yōu)橐粋€(gè)知識(shí)復(fù)習(xí)的過程，增進(jìn)了學(xué)生對(duì)有關(guān)知識(shí)的掌握。

（三）創(chuàng)設(shè)情境，激發(fā)學(xué)生學(xué)習(xí)興趣

普通心理學(xué)的第六章對(duì)記憶做了如此的描述：不同性質(zhì)材料對(duì)記憶留存率的影響不同，以散文、詩和無意義音節(jié)為例，其在人腦中留存的時(shí)間如圖2 所示，可見人們對(duì)無意義的音節(jié)遺忘得最快，長(zhǎng)時(shí)間留存情況也較散文和詩低很多，因此，教師要想保證學(xué)生對(duì)高中數(shù)學(xué)知識(shí)內(nèi)容的記憶，延長(zhǎng)相關(guān)知識(shí)留存的時(shí)間，還需要轉(zhuǎn)變一貫的教學(xué)方式，加強(qiáng)平時(shí)知識(shí)點(diǎn)對(duì)學(xué)生的刺激，以提高知識(shí)在學(xué)生腦中的留存率。鑒于高中數(shù)學(xué)教學(xué)內(nèi)容知識(shí)點(diǎn)分散且枯燥，筆者在課堂教學(xué)中十分注重從學(xué)生角度出發(fā)，調(diào)動(dòng)學(xué)生的學(xué)習(xí)興趣。如在“直線與平面垂直的判定定理”教學(xué)中，筆者提取了教學(xué)重點(diǎn)：直線與平面垂直的定義和難點(diǎn)；直線與平面垂直的判定定理。教師在導(dǎo)入教學(xué)中為學(xué)生放映了周一升國(guó)旗的視頻，用以加強(qiáng)學(xué)生對(duì)直線與平面關(guān)系的理解，生動(dòng)的視頻內(nèi)容很快對(duì)學(xué)生形成了視聽刺激，加深了學(xué)生對(duì)直線與平面垂直的直觀想象，深化了其對(duì)知識(shí)的記憶，也提高了學(xué)生大腦對(duì)有關(guān)知識(shí)的保存率。

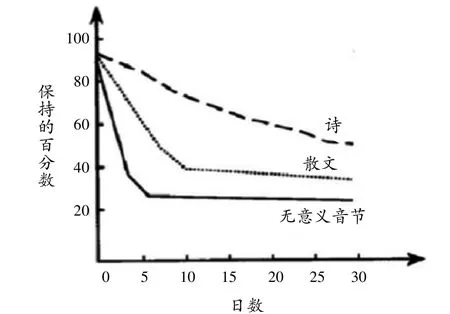
圖2 不同材料對(duì)記憶留存率的影響

（四）運(yùn)用工具增強(qiáng)學(xué)生理解記憶

從增強(qiáng)新知識(shí)對(duì)學(xué)生的刺激角度提升學(xué)生對(duì)記憶的保存率，先進(jìn)教學(xué)設(shè)備、工具和一些輔助思維的手段也能發(fā)揮出較高的價(jià)值，如交互式白板和思維導(dǎo)圖，教師也可根據(jù)教學(xué)需求和現(xiàn)實(shí)條件將二者結(jié)合，提高學(xué)生對(duì)新知識(shí)的理解能力，以加深其對(duì)有關(guān)知識(shí)點(diǎn)的記憶。筆者在“解三角形”的教學(xué)中就以真實(shí)題型為例，利用思維導(dǎo)圖幫助學(xué)生歸納了題型涉及的知識(shí)點(diǎn)，并將思維導(dǎo)圖以交互式白板的途徑呈現(xiàn)出來，根據(jù)學(xué)生的理解對(duì)思維導(dǎo)圖中的內(nèi)容進(jìn)行拓展，與學(xué)生共同推導(dǎo)出解題思路，進(jìn)而增強(qiáng)學(xué)生對(duì)單元知識(shí)運(yùn)用的記憶，實(shí)現(xiàn)學(xué)生對(duì)有關(guān)知識(shí)點(diǎn)的長(zhǎng)時(shí)間留存。

人腦的潛力是無限的，但也要遵循規(guī)律科學(xué)地開發(fā)，避免一味地填充新知識(shí)，否則不為學(xué)生的復(fù)習(xí)和記憶留出時(shí)間，只會(huì)讓學(xué)生倍感壓力，從而將其學(xué)習(xí)興趣消耗殆盡。高中數(shù)學(xué)教師在開展教學(xué)時(shí)也要注意這一點(diǎn)，要借助對(duì)艾賓浩斯遺忘曲線的運(yùn)用不斷鞏固學(xué)生對(duì)舊知識(shí)的記憶，增進(jìn)學(xué)生對(duì)知識(shí)的系統(tǒng)性整理，并以此提高學(xué)生對(duì)各類綜合題型的應(yīng)對(duì)能力。對(duì)此，教師可通過教學(xué)節(jié)奏的調(diào)整、教學(xué)情境的創(chuàng)設(shè)和教學(xué)手段的使用幫助學(xué)生鞏固所學(xué)知識(shí)，進(jìn)而促進(jìn)其數(shù)學(xué)能力的提升。