非一致地震激勵的改進位移輸入法：誤差分析與應用

李 寧，陳 浩，李忠獻

(1.天津大學 建筑工程學院 濱海土木工程結構與安全教育部重點實驗室，天津 300350；2.天津大學 中國地震局地震工程綜合模擬與城鄉抗震韌性重點實驗室，天津 300350)

如何正確計算空間差動地震動對大跨度結構的非一致效應及其影響規律，仍然是抗震研究的熱點問題[1-3]。為了保證結構的安全，考慮到設計及應用的方便，需采用恰當的計算方法進行結構的非一致動力反應分析。通常的多點多維激勵分析方法依據地震動模擬輸入和等效輸入荷載的方式不同，分為多個類型[4-10]。時域方法不僅適用于結構線性分析，也適用于非線性分析，是當前最具有普適性和有效性的計算方法。時域內多點激勵計算方法主要有：直接求解法(direct solving method,DSM)、相對運動法(relative movement method,RMM)、位移輸入法(displacement input method,DIM)、大質量法(large mass method,LMM)[11]和大剛度法(large stiffness method,LSM)。DIM法也是當前諸多有限元工具容易實現的一般方法，在多點激勵計算中被廣泛應用。而為了考慮零頻信號或地面殘余位移，DIM尤為適合。

DIM通過引入基底位移作為激勵，求解結構響應，不同于加速度場引入慣性效應。近年來，有關學者針對DIM的計算精度、存在的問題以及解決方法等展開了研究。羅超等通過對DSM、DIM、RMM和LMM的對比研究指出，DIM方法的計算精度可以滿足工程要求。惠迎新等以跨斷層橋梁為研究對象，討論了非一致激勵下DIM和LMM的適用性以及誤差產生的原因。結果表明：DIM能夠更好考慮永久地面位移對結構響應的影響，而LMM則無法考慮，但這并不是LMM本身引起的，而是有限元實現方法不同所導致。柳國環等[12]指出，當空間結構底部單元為非經典阻尼時，DIM不會存在計算結果的不收斂問題。而國巍等[13]研究指出，DIM在隔震結構中盲目使用可能會導致嚴重的錯誤。Wilson等認為要使DIM與RMM達到相同的計算精度，則需要更小的激勵步長和積分時間步長，而田玉基等卻給出了相反的結論。杜憲亭等在上述研究的基礎上指出：在積分方法和步長相同時，RMM較DIM易得到更好的精度，而在模態分析方法中則會得到相反的結論。李永華等[14]研究指出，RMM和DIM中由于阻尼假定的不同，會導致兩個方法的計算結果存在巨大差異。在Rayleigh阻尼模型下，質量比例阻尼部分是導致誤差的主要來源，并與阻尼比的大小、激勵頻率和結構基本頻率的比值有關，而剛度比例阻尼部分不會產生誤差；在單元阻尼下，兩種方法計算結果基本一致。柳國環等也指出，DIM在考慮Rayleigh阻尼時的計算結果可能不穩定和不可靠，并提出了附加無質量束縛元和無質量剛性元的修正方法。筆者認為應將結構考慮為Rayleigh假定和非比例阻尼假定兩類體系對待。

本文采用Rayleigh阻尼模型，在對多點激勵分析理論以及現有方法分類探討的基礎上；研究了DIM的適用條件，討論了其計算精度影響因素等，并基于理論分析提出和驗證了適用于空間結構非一致激勵分析方法：改進的IDIM方法(improved DIM)，該方法可推廣用于大型結構非一致激勵的動力響應計算。

1 DIM和MRE修正方法

1.1 DIM的理論分析

對于在地面上剛性連接的集中質量結構分析模型，其地震激勵下增量動力平衡方程為

(1)

(2)

通常，采用集中質量進行建模，則Mts=0；于是式(2)可以化簡為

(3)

(4)

式(4)即為DIM法求解地震差動結構反應的式子。

1.2 MRE修正方法

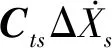
為了避免改動計算程序降低操作復雜性，MRE法的分析示意圖如圖1所示。

圖1 MRE建模示意圖Fig.1 Sketch of model adopted in MRE

在采用MRE進行建模時，可通過比較設置無質量剛性元前后結構的自振特性是否一致，判斷剛性元的剛度是否足夠。同時，應注意附加節點S處的質量為零。MRE修正后，由于DIM中忽略的阻尼力直接通過無質量剛性元顯著影響該剛度單元的相對位移和內力，對原結構各質點的影響甚小，從而巧妙避免了DIM的誤差問題。柳國環等采用商用軟件，實例分析驗證了MRE的合理性。然而，直觀地可以看出，對剛度比例阻尼系數β較大的結構，底部剛性元尺度、相對剛性大小可能導致MRE方法并不具有通用性。下面將通過實例進行分析并指出具體原因，提出修正思路。

2 算例大跨結構模型及MRE的誤差分析

2.1 算例模型及輸入地震動

為驗證MRE的效果，選取如圖2所示的橋梁結構進行分析，該橋梁跨徑為10 m+30 m+10 m，墩高6 m，材料彈性模量為2.1×1011N/m2，記為模型1。為驗證MRE對于任意結構的適用性，改變彈性模量為1.0×1010N/m2，橋墩高度為10 m，其余參數不變，記為模型2。原模型與MRE模型的自振周期特性對比如表1所示(T1約為1.16 s和6.53 s)，可以看出，模型中的無質量剛性元未引起體系前幾階變化。

表1 橋梁結構模態信息Tab.1 The modal information of bridge structure

圖2 橋梁結構有限元模型簡圖(m)Fig.2 Finite element model sketch plot of bridge structure (m)

2.2 MRE法的誤差分析

因DSM可以視為理論上的精確解，因此本文定義計算誤差η為

(5)

式中：f1(t)為DSM計算的結構響應；f2(t)為DIM或MRE的計算結果。

圖3和圖4分別給出了阻尼比為5%時，模型1和模型2采用DIM計算的橋墩1墩頂位移和墩底內力的響應峰值誤差以及地震動速度增量峰值分布圖。由計算結果可知，對于模型1，墩頂位移峰值誤差的變化范圍為0.01%～0.42%；墩底剪力變化范圍為113.53%～406.78%。墩底彎矩為15.57%～77.04%；對于模型2，墩頂位移峰值誤差的變化范圍為0.01%～1.29%；墩底剪力誤差的變化范圍為130.79%～1 010.76%；墩底彎矩誤差的變化范圍為11.29%～390.47%。可以看出，DIM計算的墩底剪力和墩底彎矩相比于墩頂位移有著不可忽略的誤差。

圖3 模型1采用DIM計算反應誤差分布Fig.3 Error distribution of model 1 with DIM

圖4 模型2采用DIM計算反應誤差分布Fig.4 Error distribution of model 2 with DIM

表2 模型1響應峰值誤差與地震動速度增量峰值的相關性Tab.2 Correlation between the maximum response error of model 1 and the maximum incremental velocity of GMs

表3 模型2響應峰值誤差與地震動速度增量峰值的相關性Tab.3 Correlation between the maximum response error of model 2 and the maximum incremental velocity of GMs

表4給出了2橋梁模型和采用MRE的峰值誤差最大值。對于模型1，MRE法給出的橋墩1墩頂位移、墩底剪力和墩底彎矩的計算誤差最大不超過0.41%，0.76%和1.19%；而對于模型2，MRE法給出的橋墩1墩頂位移、墩底剪力和墩底彎矩的計算誤差最大達到了1.29%，27.21%和8.95%。上述計算結果表明：MRE法對相對短周期結構(模型1)具有良好的修正效果；但對于形如模型2的長周期結構，仍存在無法忽略的誤差。需要說明的是，此處使用MRE的剛性元，僅考慮了不導致體系前5階模態改變，尚未深入考慮模態截止階數的影響。因此，MRE方法不具有通用性。

表4 不同模型的計算誤差最大值Tab.4 The maximum analysis error of different models %

2.3 誤差源和模擬方法的進一步探討

為尋找MRE方法對于類似模型2所示結構計算的誤差來源，本節進一步分析。對比模型1和模型2發現，兩模型自振特性不同，進而導致剛度比例阻尼系數β大小不同。對于模型1，阻尼比為5%時，比例阻尼系數以前兩階模態進行計算，剛度比例阻尼系數僅為0.007 4，對于模型2，則為0.048 4。此時，剛度很大的無質量剛性元的牽連自由度也有較大的剛度比例阻尼反力產生，導致計算誤差。理論上，當節點S1和節點S處的質量為零時，由結構動力學可知，有式(6)成立

(6)

2.4 MRE法誤差來源的數值驗證

為驗證上述探討的正確性，圖5給出了模型1和模型2在NGA953地震動(MUL279方向)作用下，結構阻尼比為10%時(為明確誤差來源而設置)，無質量剛性元節點S和節點S1處的位移時程、速度時程以及橋墩底部的剪力時程。由圖5可以看出：對于模型1，節點S1的位移時程和節點S處的位移時程相吻合；但對于模型2，節點S1處的位移時程并不等于節點S處的位移時程。也可以看出，對于模型1和模型2，節點S1處的速度時程為零，即動力時程只有位移場施加了，程序未考慮牽連速度。由于模型2的S處位移時程存在誤差，導致其速度時程也會存在誤差，最終使得剪力存在誤差，如圖5(c)所示。應當注意到，S1處的位移時程和速度時程為NGA953地震動的位移和速度時程。

圖5 結構響應時程Fig.5 Structural response time histories

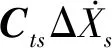
3 改進DIM方法的提出及數值驗證

為避免前述所有模擬中可能的誤差源，本節在MRE法的基礎上，給出僅修正激勵和同時修正模型和激勵兩種修正方法，便于軟件實現和選用。

3.1 同時考慮模型及激勵(I1-DIM)

上述分析指出，MRE方法修正后，DIM計算時，節點S處的位移和速度時程可能并不等于S1的位移、速度時程，即和原始地震動時程存在差異。本文根據式(6)，建議對輸入的位移時程進行修正，如圖6(a)所示，即

(7)

3.2 僅考慮動力激勵(I2-DIM)

圖6 改進的DIM方法Fig.6 Improved DIM methods

3.3 數值驗證

本節仍采用前述模型2及地震動。圖7給出了NGA953(MUL279)地震動激勵下，結構阻尼比為20%時，采用二種修正后DIM計算的、無質量剛性元節點S和節點S1處的位移時程、速度時程以及橋墩底部的剪力時程。

圖7 結構響應時程Fig.7 Structural response time histories

由圖7可以看出：當采用I1-DIM修正后，盡管約束S1的位移時程不再等于原始地震動位移時程，且速度時程仍恒為零，但橋墩底部S處的位移時程和速度時程均等于原地震動，即，模型非一致激勵輸入是正確的。橋墩底部的剪力時程也和DSM的計算結果一致，驗證了I1-DIM法的正確性。采用I2-DIM，橋墩底部S處的速度時程不再為零，其位移時程和速度時程也均等于原始地震動時程，且其修正后的墩底剪力也幾乎完全等于DSM結果。即：采用I2-DIM后的計算結果也能達到計算精度的要求。表6給出了在不同阻尼比以及前述所有地震動激勵下，采用I1-DIM和I2-DIM計算的橋墩1墩頂位移、墩底剪力和彎矩的峰值誤差最大值，可以看出，最大誤差不超過2.95%。至此，前述提出的兩種修正方法，對于任意阻尼系數和任意地震動均具有適用性，且適用于非線性通用計算分析平臺使用。

表6 I1-DIM和I2-DIM的計算誤差最大值Tab.6 Maximum error using I1-DIM and I2-DIM %

I1-DIM方法和I2-DIM方法仍存在較小的計算誤差，根據本文前述對誤差的探討，此時誤差來源應該是信號處理、積分步長不同所致。為了分析這種差異所引入誤差大小，本文計算了在僅輸入加速度和僅輸入速度時程時，模型2在地震動激勵下的峰值誤差最大值，如表7所示。由表7可知：在不同阻尼比下，最大誤差不超過4.21%，僅設置加速度激勵時誤差最大。同時對比墩底約束處的位移、速度時程可知，原地震動已正確輸入，在此不再贅述。據此建議，只要能保證橋墩底部的原始地震動時程等于激勵地震動時程，均可達到較好的計算精度。同時，也可看出，信號處理的差異以及積分步長等的不同所造成的計算誤差一般工程可接受的。

表7 不同時程信號輸入時的誤差最大值Tab.7 Maximum error of different input time history %

圖8給出了TCU068地震動(考慮了2個墩的到時差和加速度幅值比為1∶0.75，2基底處存在不同幅值的殘余位移)激勵下，采用IDIM計算下的模型2橋墩1墩底剪力時程和墩頂位移時程，可以看出，改進的DIM也可以考慮殘余位移和內力，對于跨斷層橋梁同樣具有適用性。

圖8 結構響應時程Fig.8 Structural response time histories

步驟1對有限元模型施加恒荷載、靜風壓力或水流擬靜力載荷后，分析非剛體模態特征是否合理以及恒載效應是否可以考慮。若可考慮則進行步驟2；若不合理或不能考慮(例如：底部約束釋放引起變形回彈)，執行步驟3。理論推導可知，大質量法除了如下述大剛度法可能引入舍入誤差外，還有源自式(2)右端第一項誤差，故本文不建議使用。

步驟2明確大剛度法是否會導致計算失效或引入不可接受的舍入誤差(一般施加大剛度取該方向總剛度的106倍)。若結構中無弱連接構件(小剛度的支座、支撐等)，也無屈服后可能發生剛體變位的組件，則可以采用大剛度法計算；否則進行步驟3。

步驟3建議采用DIM試算，檢驗程序對激勵時程是否考慮了數值微分(通過對比約束處激勵速度時程是否正確來判斷)。若分析程序未考慮數值微分，則采用本文提出的IDIM進行計算(以I1-DIM分析即可)；若分析程序具備數值微分功能，尚應檢驗是否有不合理的激勵信號分量產生，若有則需要濾波或信號處理后，以I2-DIM形式輸入分析。

步驟4最后驗證原結構底部的激勵時程是否等于原始地震動時程。

4 結 論

本文針對位移輸入法中存在的問題，為了方便其在有限元軟件中的合理應用，在理論分析和對比校核的基礎上得到了如下結論：

(1) 考慮Rayleigh阻尼，DIM存在不可忽略的計算誤差，誤差大小與輸入地震動的類型和剛度比例阻尼系數β相關，且隨著β的增大和脈沖效應的增強而增大，在分析中應引起注意。

(3) 明確了DIM類型計算誤差——MRE方法對剛度比例阻尼系數較小的結構具有較好的適用性，但對于剛度比例阻尼系數較大的結構則不再適用性。本文建議了2種IDIM方法，對大跨度結構非一致激勵反應分析均能夠達到很好的計算精度。

(4) 綜合多種算法的優劣，給出了分析空間非一致激勵的結構響應分析流程，可以合理考慮非一致地震動潛在破壞性效應，且通用性強，計算準確度，建議采用。

后續將進一步探索非比例阻尼效應和地震動不確定性的影響等研究工作。