諧波減速器凸輪磨削加工誤差原因分析與改進方法

谷甲甲， 石立騰， 唐江楓

（廣東省高性能伺服系統重點實驗室 珠海格力電器股份有限公司， 廣東 珠海 519070）

0 引言

諧波減速器具有傳動比大、體積小、傳動精度高等優點被廣泛應用于工業機器人、航空航天、雷達、醫療器械等領域[1-2]。諧波減速器主要由波發生器、柔輪和剛輪三大部件組成，波發生器使柔輪產生可控的彈性變形波，通過與剛輪的互相作用，實現運動和動力的傳遞。波發生器是由柔性軸承和具有特定幾何外輪廓的凸輪組成， 凸輪的外輪廓與柔性軸承的內圈配合迫使柔輪軸承變成凸輪的等距線，因此凸輪的外輪廓直接影響波發生器的形狀。諧波減速器的傳動性能受波發生器作用下的柔輪波動變形影響， 因此提高凸輪外輪廓的加工精度對諧波傳動至關重要[3]。 諧波減速器凸輪量產通常采用專用隨動磨床磨削加工，這些專用磨床一般是在FANUC 數控系統的基礎上開發一些優化模塊， 能夠高效率加工各種廓線類型的凸輪結構。 受限于專用磨床設備資源，在研發階段采用普通隨動磨床加工凸輪也是常見的方式， 本文以某款諧波減速器凸輪為例， 闡述設備A 試制過程中加工誤差出現的原因及其相應的處理方法。

1 凸輪加工誤差的研究方向

凸輪加工誤差的類別主要有三類[4]：機床及加工工藝系統誤差、數控系統誤差、編程誤差。 由于凸輪加工采用高速砂輪進行磨削， 因此加工過程中磨削顫振對凸輪表面加工質量的影響是不能忽略的。 劉濤等[5]基于非圓輪廓磨削幾何運動學特性，將“工件-砂輪”系統進行等效簡化建立了非圓輪廓磨削加工的動力學模型， 研究結果表明磨削加工不同輪廓位置時的振動狀態存在明顯差異。吳克堅等[6]從加工工藝系統誤差方向研究了磨削加工過程中由于砂輪半徑變化、X 軸對刀誤差、C 軸對刀誤差， 并對如何減小這類誤差提供了解決措施。劉雄偉等[7]從控制電路、伺服系統等方面研究了數控系統誤差。 劉平等[8]從逼近誤差、插補誤差、圓整誤差三個方面研究了編程誤差及對策。 在凸輪加工在線補償方面，杜柳青等[9]通過建立凸輪X-C 軸聯動加工通用補償模型，為凸輪類零部件加工在線補償提供了可行方案。 在非圓隨動磨削運動模型方面，俞紅祥等[10]提出多軸隨動磨削控制方式來提高磨削加工精度。

本文主要從凸輪磨削點位形成原理出發， 分析設備A 在磨削諧波凸輪時，始終存在加工誤差較大的問題，對該問題產生原因進行分析并提出改進方法。

2 各點位形成原理

2.1 模型概述

本文以某型號諧波減速器的凸輪為研究標的。 該凸輪是余弦型凸輪，輪廓方程為

式中：設備A 所采用的砂輪半徑rr為250mm，θ 為凸輪廓線關于凸輪長軸的極角。

2.2 誤差形成原因

通過查閱相關資料，設備A 的算法中，砂輪的中心軌跡是FANUC 系統自動計算出來的，只需要給出工件輪廓的坐標和砂輪的半徑，利用FANUC 的刀具半徑補償來實現。 該砂輪中心O1的運動軌跡是凸輪理論廓線的等距線， 即采用在凸輪回轉中心與待加工點連線方向等距增大的方法生成的，見圖1 所示。

對于凸輪類零件輪廓的磨削，砂輪中心O1沿凸輪理論廓線的等距線運動時， 砂輪外廓線與凸輪理論廓線不是相切關系而是相交關系（長軸和短軸處除外），導致工件被過度磨削（失真），如圖1 所示。為使被加工出的凸輪廓線保真， 砂輪切削運動所形成的包絡應為凸輪的理論廓線。 根據包絡關系砂輪與凸輪理論廓線在C 點相切，砂輪中心O2在過C點的法線上，見圖1。

根據圖1 中的幾何關系，凸輪廓線在θ 處的法線與極徑的夾角μ 為

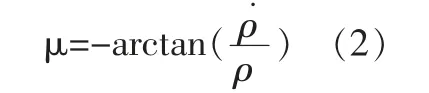
圖1 砂輪磨削示意圖Fig.1 Grinding wheel grinding

式中： ρ˙—凸輪廓線極坐標方程關于極角θ 的一階導數。

由余弦凸輪的對稱性， 對其在0°～90°范圍內凸輪理論廓線的法線轉角變化規律進行研究。 以凸輪廓線的極角θ 為橫軸，轉角μ 為縱軸，見圖2。

由圖2 可知，在凸輪長軸（θ=0°）和短軸（θ=90°）時，凸輪理論廓線的法線與極徑的夾角為0°，即此處砂輪與凸輪是相切關系不存在過度磨削現象；在其他位置凸輪理論廓線的法線與極徑的夾角不為0°，變化趨勢呈拋物線，砂輪與凸輪是相交關系存在過度磨削現象； 凸輪理論廓線的法線與極徑的夾角在極角θ=45.507°處達到最大值2.0271°。

圖2 凸輪理論廓線的法線與極徑的夾角Fig.2 Angle between normal and polar diameter of theoretical cam profile

僅有上述的凸輪理論廓線的法線與極徑的夾角，還不能確定砂輪與凸輪理論廓線的干涉程度， 即過度磨削量。 通過砂輪對凸輪理論廓線包絡關系分析，采用周向和徑向干涉量對過度磨削程度進行量化分析。

3 過度磨削量分析

3.1 周向干涉量

由圖1 的幾何關系， 處于O1點的砂輪與凸輪理論廓線的交點為C 和D，用∠COD=α 的夾角表示干涉范圍，即周向干涉量

根據式（3）的求解結果，分析在不同極角θ 下砂輪與凸輪理論廓線周向干涉量變化規律。以凸輪廓線的極角θ為橫軸，周向干涉量α 為縱軸，見圖3。

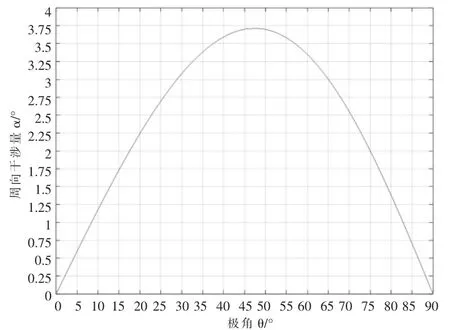
圖3 砂輪與凸輪理論廓線周向干涉量Fig.3 Circumferential interference of theoretical profile between grinding wheel and cam

由圖3 可知，在凸輪長軸（θ=0°）和短軸（θ=90°）時，砂輪與凸輪理論廓線無干涉， 即此處砂輪與凸輪是相切關系不存在過度磨削現象；在極角θ=47.5°時，砂輪與凸輪理論廓線干涉范圍達到最大為3.714°。

3.2 徑向干涉量

徑向干涉量是砂輪對凸輪的過度磨削評價的重要指標，根據圖1 的幾何關系對徑向干涉量進行表征。 由圖1的幾何關系， 砂輪中心在極角θ 處的法線通過點O1和點F；點O 與點E 的距離為

由圖4 可知，在凸輪長軸（θ=0°）和短軸（θ=90°）時，砂輪與凸輪理論廓線徑向干涉量為0mm， 即加工此處時不產生干涉；在極角θ=46°時，砂輪與凸輪理論廓線徑向干涉量達到最大為0.013mm。

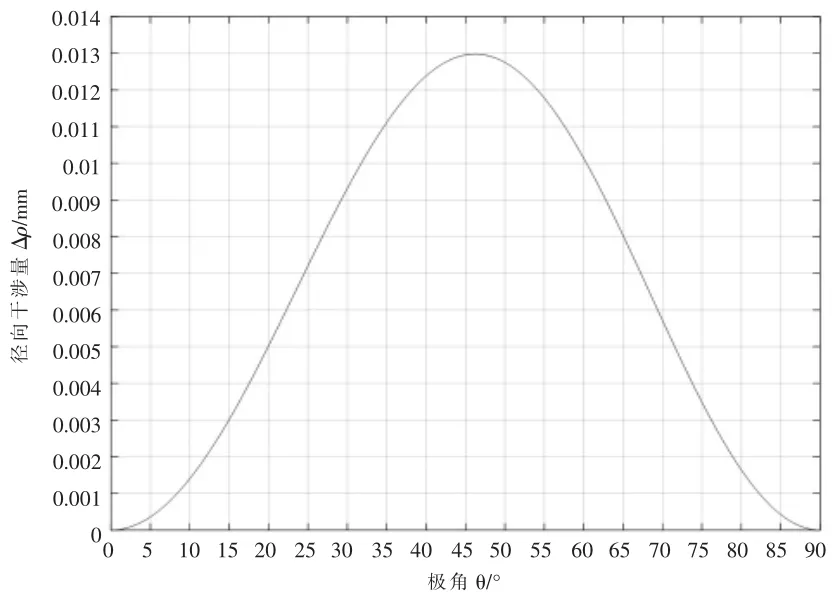
圖4 砂輪與凸輪理論廓線徑向干涉量Fig.4 Radial interference of theoretical profile between grinding wheel and cam

4 改進方法

綜合上述分析，砂輪中心處于點O1加工凸輪是不合理的將產生過度磨削現象，應使砂輪中心處于點O2。根據圖1 中的幾何關系，點O2的極坐標為

根據諧波減速器凸輪的結構特點以及設備A 磨削試制方案的特性，運用包絡理論，計算在設備A 的砂輪半徑條件下，不產生磨削干涉的砂輪中心運行軌跡式（10），然后在極坐標系中根據砂輪半徑進行換算， 得到新的凸輪廓線點位式（11）。將新凸輪廓線輸入設備A，設備A 將按照新凸輪廓線沿極徑等距生成砂輪中心運行軌跡（即包絡求出的砂輪中心軌跡）生成砂輪中心運行軌跡，即可得到符合要求的被加工凸輪廓線。

5 結論

非圓廓線上任一點的法線夾角和極角是非恒相等的，兩者之間的關系不能混淆需要進行明確區分。 設備A沒有能夠實現復雜廓線的圓弧化離散功能， 而將余弦凸輪廓線簡單的沿極徑方向等距作為砂輪中心軌跡規劃會造成很大的磨削干涉，引起最終工件尺寸誤差較大。根據包絡關系求出點O2作為砂輪中心的軌跡運動點，從而避免產生過度磨削現象。