持續負溫環境下入模溫度對水泥水化熱的影響及預測模型

龍朝飛，張戎令，郭海貞，段運，肖鵬震，段亞偉

(1. 蘭州交通大學土木工程學院，甘肅 蘭州，730070；2. 蘭州交通大學道橋工程災害防治技術國家地方聯合工程實驗室，甘肅 蘭州，730070；3. 甘肅暢隴公路養護技術研究院有限公司，甘肅 蘭州，730070)

水泥水化是一個放熱過程，期間放出的熱量會影響混凝土的凝結和硬化[1]。由于我國三北地區以及青藏高原等地區均存在著大量多年凍土，凍土區鉆孔灌注樁等深埋混凝土一經澆筑將立即處于負溫環境中[2]。水泥的水化速率與環境溫度有關[3-6]，而低溫條件下的水化改變了水泥基材料的流變和凝固特性[7]；當環境低于-5 ℃時，由于新拌混凝土中92%的水會結冰，水與水泥基本不發生水化反應，嚴重影響了水泥的水化進程[8]。因此，研究負溫環境下水泥的水化特性與放熱規律具有重要意義。

入模溫度是影響混凝土絕熱溫升和溫升速率的一個重要因素，而混凝土的絕熱溫升和溫升速率反映早齡期混凝土的水化速率和水化程度[9]。有研究表明，提高混凝土初始入模溫度將加速膠凝材料的水化，并縮短水化反應持續時間[10]。因此，鉆孔灌注樁澆筑時，若入模溫度過高，則水化反應生成的大量熱量將對凍土產生較大的熱擾動，這可能會破壞凍土的穩定凍結狀態，使得其凍結強度降低甚至融化，最終導致樁的承載力大幅下降[11-12]。因此，有必要在試驗基礎上對多年凍土區鉆孔灌注樁水泥水化熱進行定量分析，且應考慮入模溫度這一重要變量。

目前，國內外學者已經針對水泥水化放熱特性進行了一系列研究，并建立了一系列水化放熱的預測模型。MEINHARD 等[13]建立了改進的普通硅酸鹽水泥的熱釋放速率模型，并將其推廣到混合水泥中，發現模型預測結果與直流試驗數據吻合良好。李瑤[14]研究了低溫環境中復合膠凝材料的水化規律，建立了基于Krstulovic-Dabic 方程的硅酸鹽水泥-硅灰復合膠凝材料的水化動力學模型。該模型分段模擬整個水化歷程，進一步揭示了復合膠凝材料在低溫下的水化動力學反應機理。王起才等[15]建立了持續低溫環境下水泥水化放熱計算模型，較好地預測了不同低溫環境下水泥水化放熱量隨齡期變化的規律。DAI等[16]研究了養護溫度和水灰比耦合效應對水泥水化熱的影響并提出了預測0 ℃以上和負溫養護下的水泥漿體的水化熱計算公式，發現水泥漿的累計水化熱隨養護溫度的升高而增加；在負溫養護條件下，水泥漿的累計水化熱隨水灰比增大而降低。

上述學者雖然研究了不同低負溫環境下水泥的水化放熱規律，并建立了一系列水化熱預測模型，然而，有關入模溫度、負溫耦合效應對水泥水化熱影響的研究較少。因此，本文作者重點研究持續負溫環境下入模溫度對水泥水化放熱的影響規律，并建立相應的水化熱預測模型，以期為我國三北地區以及青藏高原等凍土區水泥水化熱的預測提供理論依據。

1 試驗

1.1 試驗原材料

本試驗采用甘肅省永登縣祁連山水泥公司生產的P.O42.5 級普通硅酸鹽水泥，水泥檢測指標如表1所示。試驗用水為蘭州市自來水，試驗用水檢測指標如表2所示，試驗水灰比為0.38。

表1 P.O42.5硅酸鹽水泥技術指標Table 1 Technical indexes of P.O42.5 Portland cement

表2 試驗用水檢測指標Table 2 Test water detection indexes

1.2 試驗方案

凍土區按照年平均地溫可分為極穩定型凍土(溫度θ＜-5 ℃)、穩定型凍土(-5.0 ℃≤θ＜-3.0 ℃)、亞穩定型凍土(-3.0 ℃≤θ＜-1.5 ℃)、過渡型凍土(-1.5 ℃≤θ＜-0.5 ℃)及不穩定型凍土(-0.5 ℃≤θ≤0.5 ℃)等[17]。考慮到大多數多年凍土溫度分布屬于穩定型凍土，故本試驗選取-5 ℃作為持續負溫環境溫度，并以標準養護下的試件作為對照，模擬凍土環境對水泥水化造成的影響。持續負溫環境采用大氣模擬箱進行模擬，大氣模擬箱溫度恒定調控為(-5±1)℃，該環境下的相對濕度為70%。標準養護在溫度為(20±2) ℃，相對濕度為95%的標準養護室內進行。

由于GB 50164—2011[18]規定冬季施工應控制混凝土的入模溫度不低于5 ℃，因此結合凍土地區持續低負溫的施工環境，試驗選取5，10，15 和20 ℃這4 種入模溫度工況。測定水泥水化熱的方法主要是直接法和溶解熱法。由于直接法無法消除溫升對水化反應速率的影響，且試驗耗時較長，試驗過程中所受干擾較大，一般只能測得前7 d的水化熱。而溶解熱法可以測得直接法未能測得的瞬時發熱量和長齡期的水化熱，便于測定水泥的水化熱量尤其是長齡期水泥水化熱量。因此，本文依據GB/T 12959—2008[19]中的溶解熱法進行不同環境條件下水泥水化熱的測定。該測試方法原理如下：依據蓋斯定律，反應的熱效應只與體系的初態和終態有關，而與反應途徑無關，在熱量計周圍溫度一定的條件下，用未水化的水泥與一定齡期的水化水泥分別在一定濃度的標準酸溶液中溶解，測得溶解熱之差，作為該水泥在該齡期內所放出的水化熱。采用溶解熱法分別測試標準養護和負溫環境下不同入模溫度工況對應的齡期為3，7以及14～63 d(遞增幅度為7 d)的水泥凈漿的累計水化熱，其中3，7，14，21 和28 d 時的試驗數據用于建立預測模型，35，49 和63 d 對應的試驗數據用于驗證預測模型的精度。設計試驗分組如表3所示，其中SC為標準養護下的試驗組，NE為-5 ℃環境下的試驗組。

表3 不同入模溫度下試件分組設計Table 3 Experimental grouping design under different molding temperature conditions

1.3 試驗步驟

圖1所示為整個試驗的流程。首先，用孔徑為0.9 mm 的方孔篩篩取水泥，并將水泥充分混合均勻。然后，依據試驗水灰比稱取500 g水泥和190 g水，將水泥和水分別裝入塑料袋和塑料水壺中，之后一并放入恒溫養護箱內預溫養護24 h。依據試驗設置的4種入模溫度工況，調節養護箱溫度使得各工況下溫度變化幅度不超過±1 ℃。在進行水化熱試驗時，將預溫完成后的水泥和水從恒溫養護箱中取出，快速地倒入水泥凈漿攪拌機中進行攪拌。攪拌時，通過溫控系統將攪拌溫度分別控制在5，10，15 和20 ℃，與入模溫度保持一致。攪拌完畢后及時留置試驗試樣，制備出的水泥凈漿試樣分別放入標準養護和負溫環境中進行養護。待試樣到達指定齡期時將試樣取出，放入無水乙醇中，以終止其水化作用。在進行水化熱測試之前，將樣品從酒精中取出，在烤箱中干燥2 h。最后，將樣品放入一個密封的玻璃瓶中，并儲存在干燥器中，采用溶解熱法測定水泥的水化熱。

圖1 水泥水化熱測定試驗流程Fig.1 Testing process of cement hydration heat

2 試驗結果與分析

2.1 不同環境條件下入模溫度對水泥水化進程的影響

圖2所示為標準養護和持續負溫環境下不同入模溫度工況對應的水泥累計水化熱和水化放熱速率。圖3所示為標準養護和持續負溫環境下不同入模溫度工況對應的水泥水化程度。

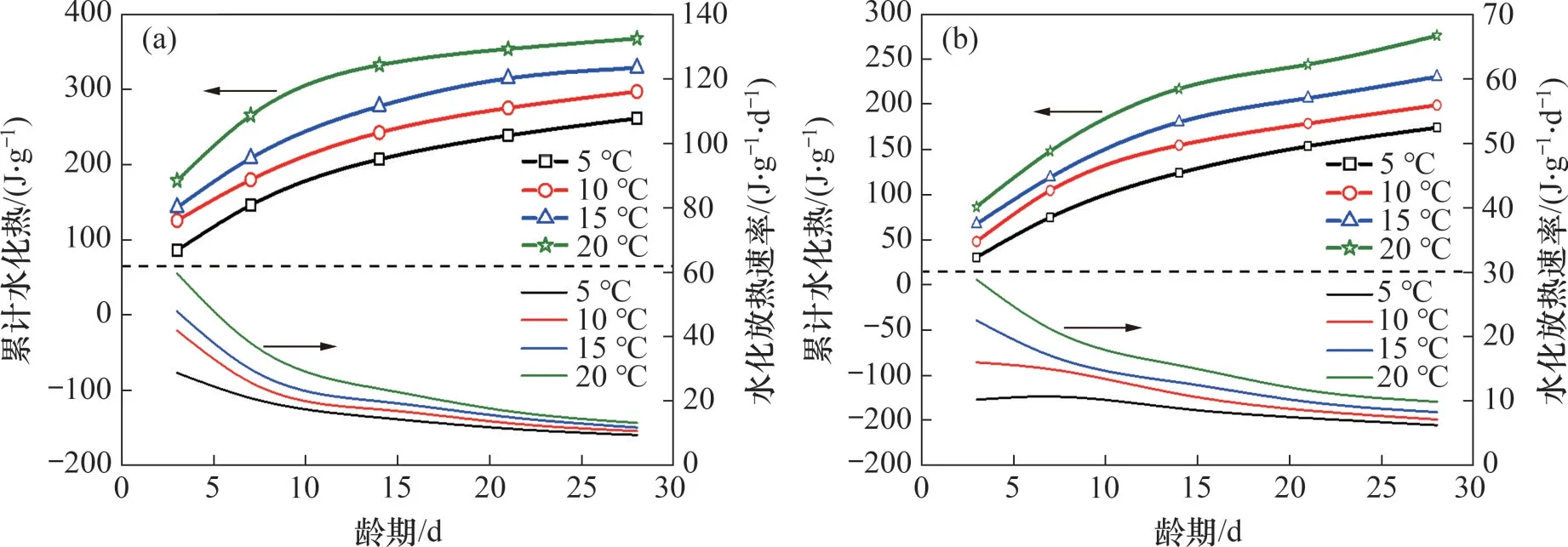
圖2 不同環境條件下入模溫度對水泥水化熱的影響Fig.2 Effect of molding temperature on hydration heat of cement under different environmental conditions

圖3 不同環境條件下入模溫度對水泥水化程度的影響Fig.3 Effect of molding temperature on cement hydration degree under different environmental conditions

水化程度α是指試驗中任意時刻累計水化熱占理論總水化熱的比例，其表達式為

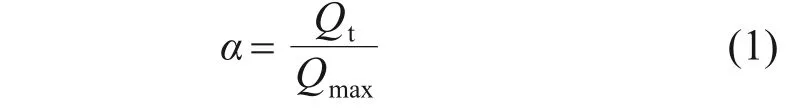
式中：Qt為水泥的累計水化熱，J/g；Qmax為根據水泥礦物組成計算得到的理論最大水化熱，J/g。

由于普通硅酸鹽水泥完全水化時的放熱量為425～460 J/g[20]，試驗中取水泥水化完全時的放熱量為454 J/g。

由圖2和圖3可見：隨著入模溫度升高，等齡期時，標準養護環境和持續負溫環境下水泥的累計水 化 熱Qt呈 現 以 下 趨 勢：Qt,SC20＞Qt,SC15＞Qt,SC10＞Qt,SC5，Qt,NE20＞Qt,NE15＞Qt,NE10＞Qt,NE5，Qt,SC20＞Qt,NE20，Qt,SC15＞Qt,NE15，Qt,SC10＞Qt,NE10，Qt,SC5＞Qt,NE5。水 化放熱速率v和水化程度α的變化趨勢與Qt的變化趨勢一致。由上述現象可以得出以下結論：

1)初始入模溫度越高，2種環境下水泥的水化放熱速率就越快，累計水化熱和水化程度也越高。隨著齡期逐漸增大，水泥水化放熱速率逐步降低，水化放熱變緩。這是因為，當水膠比和養護溫度一定時，入模溫度成為影響水泥水化反應的主要因素。不同的入模溫度為水泥水化反應提供了不同的初始反應溫度，初始反應溫度升高提高了水分子與水泥顆粒有效碰撞的概率，加快了水泥水化反應的速率。在水化初期，水分供給充足，水化產物較少，結晶成核與晶體生長起主導作用，保證了水泥水化反應的有效進行；隨著水化時間延長，水泥顆粒周圍逐漸形成一層水化產物層，離子遷移變得困難，水化反應轉變為相邊界反應或擴散控制過程[21]。隨著水分不斷消耗，水化反應后期供水量不足，因此水化速率迅速減小，累計水化熱增長曲線也趨于平緩。

2)當入模溫度相同時，標準養護環境下水泥的水化放熱速率、累計水化熱、水化程度均比負溫環境下的大。這是因為，在負溫環境下，隨著養護時間延長，水泥凈漿會由初始入模溫度的高能態向養護溫度的低能態轉變，其溫度最終同環境溫度保持一致。因此，在水化初期，初始入模溫度保證了水泥水化反應的有效進行，但在負溫環境下，水泥的水化速率比標準養護環境下的低。因此，負溫環境下水泥的累計水化熱和水化放熱速率均比標準養護環境下的低。伴隨著水化反應的持續進行，雖然環境溫度為負溫，但由于水化反應會生成大量水化熱，故水泥漿內部將處于變溫狀態，使得水化反應持續進行[22]。當水化反應進行至后期，水泥漿溫度已基本同環境溫度保持一致，水泥水化放熱速率急劇降低，放出的水化熱量也大大降低。負溫使得水泥漿中較大孔隙中的水結冰，不再繼續水化，因而最終導致負溫環境下水泥的累計水化熱和水化程度低于標準養護環境下的累計水化熱和水化程度。

由圖2(a)和圖2(b)對比可見：當入模溫度為5 ℃，齡期分別為3，14和28 d時，負溫與標準養護環境下的累計水化熱比值分別為0.35，0.60 和0.67。當入模溫度上升為10 ℃時，負溫與標準養護環境下累計水化熱的比值變為0.38，0.64 和0.67。當入模溫度上升至15 ℃時，負溫與標準養護環境下累計水化熱的比值分別為0.47，0.65 和0.70。當入模溫度上升至20 ℃時，負溫與標準養護環境下累計水化熱的比值分別為0.48，0.65 和0.75。在負溫環境下，20 ℃入模溫度工況在28 d內的累計水化熱比5 ℃入模溫度工況下的高，這表明隨著入模溫度升高，負溫環境下水泥水化放熱更加充分。這是因為入模溫度升高有效地提高了負溫環境中水泥的水化反應速率，在一定程度上抵消了負溫環境對水泥水化放熱的不利影響。對比各齡期下不同環境中水泥的水化放熱速率可知：在水化早期，標準養護環境中水泥水化放熱速率明顯比負溫環境下的大，但當水化進行到后期，2種環境下水泥水化放熱速率迅速下降，但此時負溫環境下水泥水化放熱速率已與標準養護下的水化放熱速率十分接近。由此可見當水化進行至后期時，負溫抑制水泥水化的不利影響將會減弱。

2.2 不同環境下水化放熱預測模型

由于水泥水化熱是依賴于齡期的，因此，朱伯芳等[23]提出采用指數函數模型來計算水泥的水化熱：

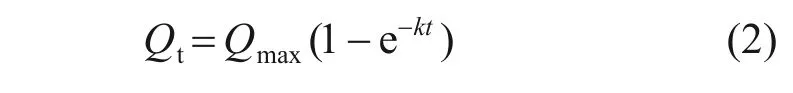
式中：t為齡期，d；k為經驗參數。

隨后，朱伯芳[24]發現復合指數函數模型用于表征水泥水化熱的效果更好：

式中：λ和c為經驗參數。

蔡正詠[25]采用雙曲線函數模型來預測水泥水化熱：

式中：m和n為經驗參數。

董繼紅等[26]基于化學反應動力學原理，發現對數函數模型對水泥恒溫水化放熱有較好的擬合效果：

式中：a和b為經驗參數。

鄧曉等[27]發現冪指函數模型對恒定-3 ℃溫度下的水泥水化規律有較好的擬合效果；

式中：γ和β為經驗參數。

為了找出最適用于持續-5 ℃環境下的水泥水化熱的預測模型，通過式(2)～(6)分別對標準養護和負溫環境下入模溫度為5 ℃和20 ℃的水化熱數據進行擬合，各模型的模擬值與實測值結果如圖4所示。由圖4可見：由于指數函數模型前期的累計水化熱增長率過快，因此，2種環境下水泥的水化熱相對誤差較大，但是其余4類模型均可較好地擬合28 d內標準養護和負溫環境下水泥的水化熱，其中雙曲線函數模型的擬合精度最高。

圖4 不同函數模型水化熱曲線擬合結果Fig.4 Fitting results of hydration heat from function models

為了進一步評價各模型預測的可靠性，試驗測定35～63 d 的水化熱，各模型預測結果如圖5 所示。其中，35，49 和63 d 齡期下不同模型所得水化熱預測值和實測值相對誤差見表4。由圖5 和表4可見：標準養護環境下，63 d時雙曲線函數模型可以較好地擬合水化熱，其相對誤差在2%以內；其余函數模型擬合結果較差，且相對誤差隨著齡期延長越來越大。當預測標準養護(入模溫度為5 ℃)工況下63 d 齡期水泥的水化熱時，式(2)，(3)和(6)的預測誤差分別為37.12%，15.55% 和29.89%；當預測標準養護(入模溫度為20 ℃)工況下63 d 齡期水泥的水化熱時，式(5)的預測相對誤差為14.15%。這表明，只有雙曲線函數模型可以較好地預測標準養護下不同入模溫度工況對應3～63 d 齡期內水泥累計水化熱。在持續負溫環境下，雙曲線函數模型和對數函數模型擬合精度均較高，相對誤差分別在3%和5%以內，其余3類模型擬合精度較差。結合圖4可以得出：無論是標準養護環境還是持續負溫環境，雙曲線函數模型均可以較好地預測3～63 d齡期內水泥累計水化熱，而對數函數模型僅可用來預測負溫環境下3～63 d齡期內水泥的累計水化熱。

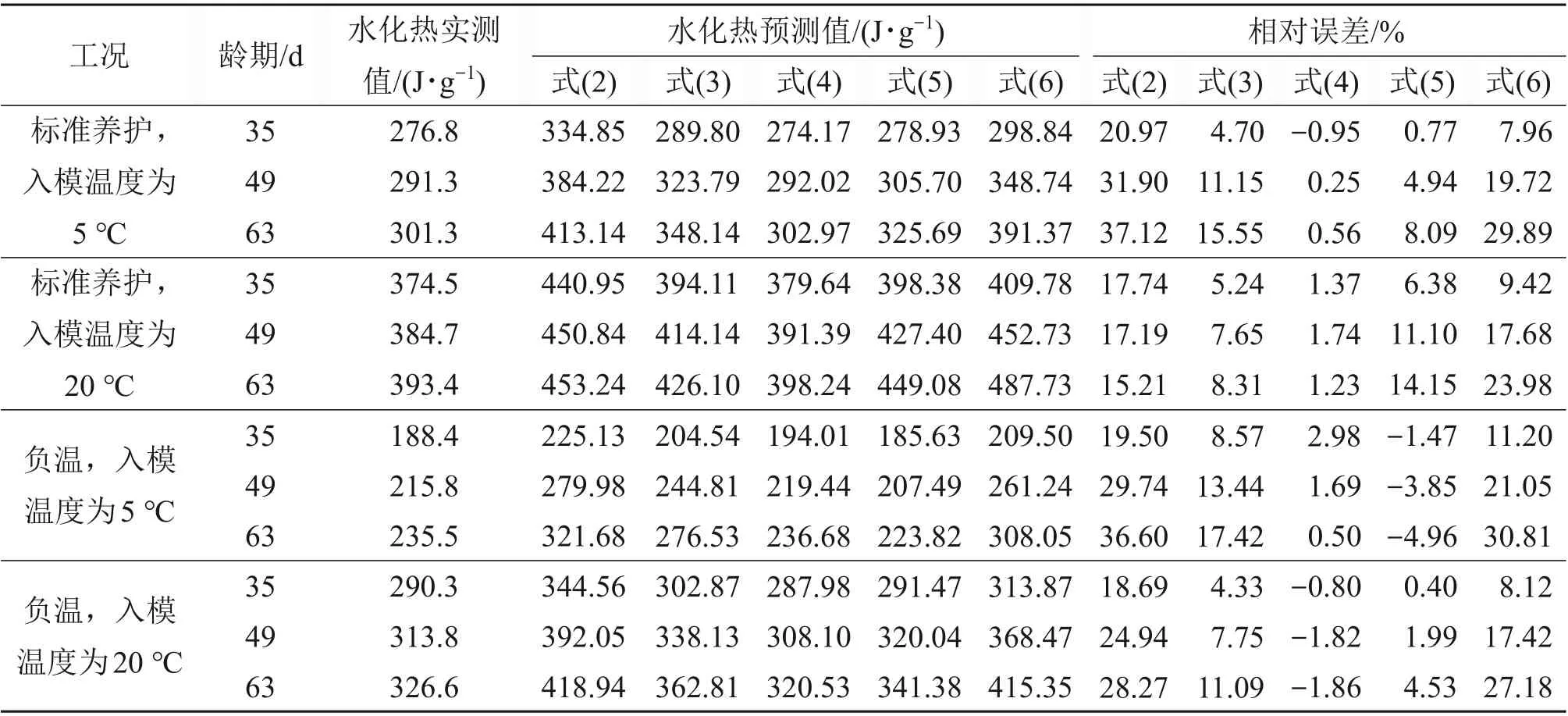
表4 各函數模型35，49和63 d內預測誤差Table 4 Prediction error of each function model within 35,49 and 63 days

圖5 不同函數模型預測35～63 d內水泥水化熱Fig.5 Heat of hydration in 35-63 d predicted by different functional models

為了驗證各函數模型在齡期63 d 以后的預測精度，將各擬合曲線中的齡期延長至為1 000 d，觀察各模型是否符合水泥水化末期水化熱的變化規律，擬合曲線延伸結果如圖6 所示。由圖6 可見：在齡期趨于無窮大時，冪指數函數模型和對數函數模型所得水化熱增長率趨于無窮，明顯不符合水泥水化規律。而指數函數模型、復合指數函數模型以及雙曲線函數模型所得水化熱增長率趨近于零，符合水泥水化的基本規律。由于指數函數模型無法較好地預測齡期3～63 d 內水泥累計水化熱，而復合指數函數模型無法較好地預測齡期28～63 d內水泥累計水化熱，因此，采用雙曲線函數模型預測不同環境條件下各齡期水泥的累計水化熱。

圖6 不同函數模型預測3～1 000 d內水泥水化熱Fig.6 Heat of hydration in 3-1 000 d predicted by different functional models

本文基于雙曲線函數模型建立負溫環境下入模溫度對水泥水化熱影響的預測模型。雙曲線函數模型擬合經驗參數如表5所示。由表5可知：在標準養護環境下，5，10，15 和20 ℃入模溫度對應的經驗參數mS和nS近似呈線性變化，如圖7 所示。因此，可以推斷出標準養護環境下水化熱模型經驗參數mS和nS與入模溫度有關，從而建立標準養護環境下入模溫度水化熱預測模型：

圖7 標準養護環境下經驗參數擬合結果Fig.7 Fitting results of empirical parameters under standard curing environment

表5 雙曲線函數模型經驗參數擬合結果Table 5 Fitting results of empirical parameters of hyperbolic function model

式中：x為入模溫度，℃。

由表5 可知：當入模溫度為10，15 和20 ℃時，標準養護環境下的經驗參數mS和nS與負溫環境下的mF和nF近似呈線性關系，因此推測負溫環境下水化熱模型的經驗參數mF和nF也與入模溫度呈線性關系。由圖8和式(7)可以得到負溫環境下入模溫度水化熱預測模型：

圖8 標準養護和負溫環境下經驗參數擬合結果Fig.8 Fitting results of empirical parameters under standard curing and negative temperature environment

2.3 預測模型驗證及誤差分析

為了驗證式(8)的精度，現將齡期為35，49 和63 d水化熱實測值與模型的預測值進行對比，結果見表6。由表6 可知：僅當入模溫度為5 ℃，齡期為35 d 時，負溫環境下的水化熱預測模型的相對誤差為3.72%；其余工況下，預測模型的相對誤差絕對值均在3%以內，精度較高。這說明，在持續負溫環境下，雙曲線函數模型中的經驗參數m和n也與入模溫度呈線性相關。因此，模型可用于預測持續負溫環境下不同入模溫度工況對應的水化熱。由于建立的持續負溫環境下入模溫度水化熱模型參數與標準養護條件相關，因此可通過標準養護條件下測定的水化熱較好地預測持續負溫環境下不同入模溫度工況對應的水化熱。由于標準養護工況下的試驗條件更容易滿足，因此，該模型可為我國凍土區水化熱預測提供參考。

表6 水化熱預測模型誤差分析Table 6 Error analysis of hydration heat forcasting model

3 結論

1)負溫環境延緩了水泥水化進程，提高入模溫度，可使標準養護和負溫環境下水泥水化放熱速率增大，負溫環境下水泥水化更加充分。但是隨著齡期增大，負溫環境下水泥水化放熱速率逐漸接近于標準養護環境下的水泥水化放熱速率，因此當水化過程持續至后期時，負溫抑制水泥水化的不利影響將會減弱。

2) 分別采用冪指數、雙曲線、對數、指數、復合指數函數模型對測定的水化熱進行了擬合。通過對比分析不同齡期下各模型對水泥水化熱的擬合結果，發現雙曲線函數模型擬合效果最好且模型擬合參數m和n與入模溫度呈線性相關。

3)建立了持續負溫環境下入模溫度-水化熱的雙曲線函數預測模型，發現該模型可以較好地預測負溫環境下不同入模溫度工況對應的水泥水化熱隨齡期變化的規律。此外，本文所提入模溫度-水化熱預測模型可通過標準養護環境下測定的水化熱預測得到持續負溫環境下各入模溫度工況對應的水化熱，可為我國高寒凍土區水泥水化熱的預測提一定的參考。