傅里葉變換微積分性質的區別、聯系及應用

陳 軍，汪 璞，安成錦，曾瑤源

（國防科技大學 電子科學學院，湖南 長沙 410073）

0 引言

傅里葉變換是“信號與系統”課程中非常重要的一種數學工具，它建立了時域與頻域之間的一一對應關系。若信號的傅里葉變換存在，則

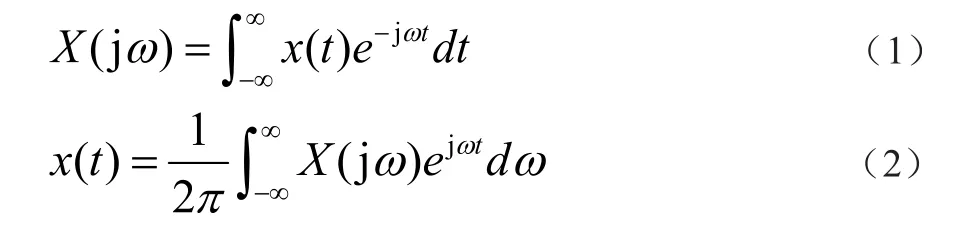
理論上，利用式（1）（2）中的積分可以實現傅里葉變換和反變換的計算。但許多情況下，利用定義式計算不僅煩瑣，而且有時候積不出來。我們更傾向于記住常用信號的傅里葉變換，再利用傅里葉變換性質來求解。但是利用性質計算傅里葉變換過程中，往往容易用錯性質，尤其是時域微積分性質。下面將從這兩條性質的定義出發，說明二者的區別和聯系。

1 微分、積分性質的內容

1.1 微分性質

1.2 積分性質

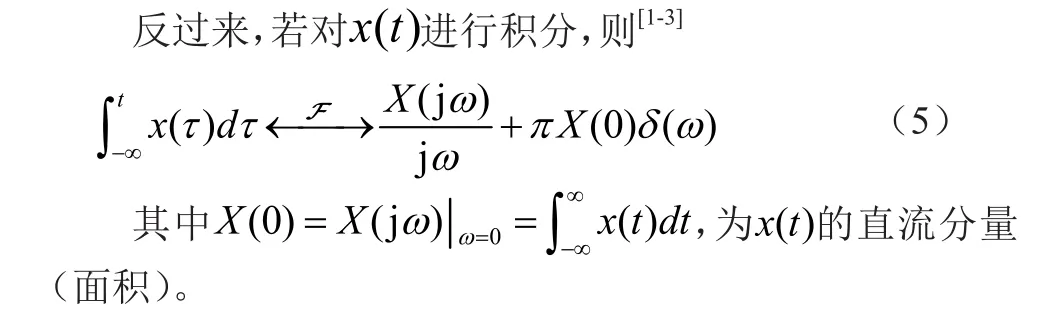
2 微分、積分性質的區別和聯系

3 時域微分性質時需要注意的問題

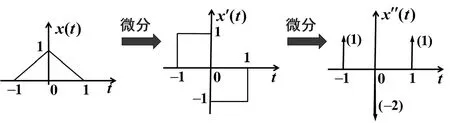
圖1 的各階微分結果

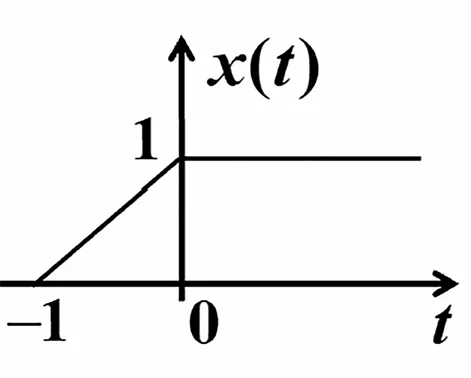
圖2 信號的波形

確。總的來說，若信號微分結果的面積為0，可以直接將微分結果的頻譜除以，即可得信號本身的頻譜；若微分結果的面積不為0，一定要用積分性質，也就是除以后，還要再加上一項。

4 微積分性質的應用舉例

對例2、例3的求解也為計算分段線性信號的頻譜提供了思路：依次對信號進行求導，直到微分結果出現沖激；計算最后一個微分結果的傅里葉變換；最后利用微積分性質得到分段線性信號的頻譜。能否用微分性質取決于微分信號的面積是否為0。

5 微分性質在系統分析中的應用

微分性質還可以用于連續時間系統的分析與求解。在時域求解微分方程，尤其是高階微分方程的零狀態響應是非常復雜的。借助傅里葉變換的微分性質，就可以將方程從時域復雜的微分方程變到頻域相對簡單的代數方程，將大大簡化系統的分析和計算。

圖3 的各階微分

6 結論

本文首先說明了傅里葉變換時域微積分性質的區別和聯系；然后通過例題說明了在使用微分性質時容易出現的問題，在利用的傅里葉變換求解頻譜的時候，只有當的面積為0時，才能直接用微分性質，否則要用積分性質；最后通過典型例題給出了求解分段線性信號頻譜的通用方法。