基于改進經驗模態(tài)分解的汽車后視鏡電機故障診斷方法

吳 駿，陸曄敏，王玉峰

（麥格納（太倉）汽車科技有限公司，江蘇 蘇州 215000）

隨著汽車技術的發(fā)展，汽車后視鏡從傳統(tǒng)的拉索式結構后視鏡轉變?yōu)橛呻姍C驅動控制，具備可自動調節(jié)位置、駐車收縮折疊和角度記憶等功能。后視鏡電機是汽車電動后視鏡的核心組成部分，其工作狀態(tài)直接影響到電動后視鏡的安全運轉。國內的電動后視鏡生產廠家缺乏完善的故障診斷系統(tǒng)，則導致不合格的汽車電動后視鏡流入市場，進而導致車輛意外事故的發(fā)生。目前在生產過程中使用的故障診斷方法是人工聽檢方法，但其存在標準不統(tǒng)一、檢測效率低、勞動強度大、損害聽力健康等局限性。振動信號作為汽車后視鏡工作發(fā)出的固有信號，能夠反映后視鏡運行狀態(tài)，為故障診斷提供了合理的依據。

電動后視鏡的振動信號是一種非線性、非平穩(wěn)信號，在分析此類信號時，以快速傅里葉變換為基礎的分析方法已不能滿足要求。目前常用的信號時頻分析方法有GABOR提出的短時傅里葉變換（STFT）、Wigner-Ville分布（WVD）和小波變換（WT）等[1]。上述的時頻分析方法在一定程度上解決了非線性、非穩(wěn)態(tài)信號分析的困難，但是都不能避開時間分辨率與頻率分辨率沖突的矛盾。HUANG于1998年提出Hilbert-Huang變換[2]，其中該方法提出了以本征模態(tài)函數為基本時頻信號，不依賴于傳統(tǒng)信號分析理論的束縛。它通過定義信號的瞬時頻率，能夠精確表達信號頻率變化，適合分析非平穩(wěn)信號[3]。

本文提出一種方法，先將振動信號進行經驗模態(tài)分解（Empirical Mode Decomposition，EMD），使用希爾伯特變換（Hilbert Transformation，HT）將每一個本征模態(tài)函數進行解調制，得到信號的瞬時頻率、瞬時幅值，根據所得的數據繪制希爾伯特譜，該希爾伯特譜包含了信號的時頻信息。對瞬時頻率與瞬時幅值取若干特征，引入BP神經網絡，對后視鏡電機故障模式分類器進行訓練，建立HHT-BP的分析模型。實驗結果表明，可以通過HHT-BP的方法判斷出汽車后視鏡電機存在的沖擊故障。

1 HHT的基本原理

希爾伯特-黃變換（Hilbert-Huang Transformation，HHT）的振動信號特征提取方法分為經驗模態(tài)分解、希爾伯特變換、本征函數特征提取3個步驟。

任何復雜的信號都是由一些相互獨立的固有模態(tài)函數（Intrinsic Mode Function，IMF）所構成，每一個IMF分量可以是線性的也可以是非線性的，對于一段數字信號x（t），經過經驗模態(tài)分解后可表示為以下等式[4]：

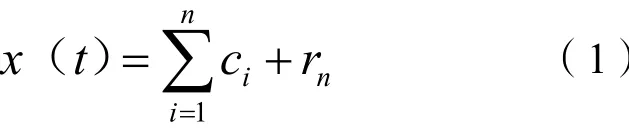
式（1）中：ci為第i階IMF分量；rn為余項函數。

對每個IMFci作Hilbert變換，算法如下：

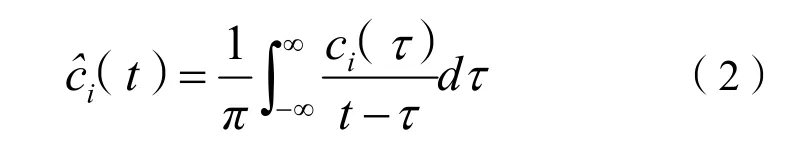
構造解析信號為：

式（3）中：ai（t）為解析信號的瞬時幅值函數；為解析信號的瞬時相位函數。

2 實驗設備與特征提取

本文所選用的測試樣品為麥格納汽車科技有限公司所提供的電動后視鏡產品，其額定工作電壓為12 V。在數據采集過程中，設置的采樣頻率為100 kHz，所使用的測振設備為壓電式振動傳感器。樣品電機與傳感器測點位置如圖1所示。

圖1 故障電機振動信號的經驗模態(tài)分解

將采集完的振動信號進行EMD分解，選取的最大分解階數為10階，圖2、圖3分別為故障電機與健康電機各自的10階IMF曲線與余項函數隨采樣點的變化情況。

圖2 故障電機振動信號的經驗模態(tài)分解

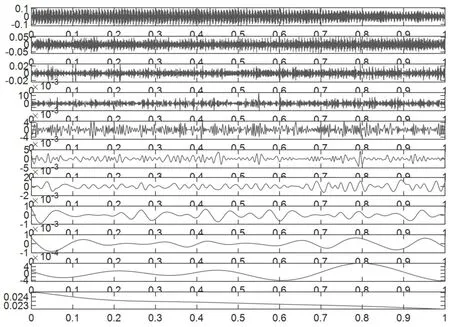
圖3 健康電機振動信號的經驗模態(tài)分解

第1節(jié)所述方法提取了樣本信號的10階IMF分量曲線與余項函數曲線。但由于在提取IMF分量時使用了3次樣條擬合的方法，引入了端點處的震蕩，需要對IMF分量進行篩選，去除與原樣本信號相關度較小的IMF分量[5]，保留與原信號相關度較大的分量。

本文定義了原始信號與IMF間的相關度函數與閾值T，相關函數的公式為：

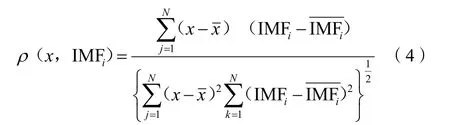
閾值選取如下公式，即：

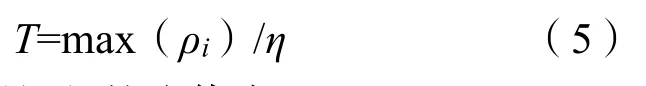
式（5）中：通常情況下η的取值為10[6]。

故障電機和健康電機各階IMF曲線與原信號的相關度分別如表1、表2所示。

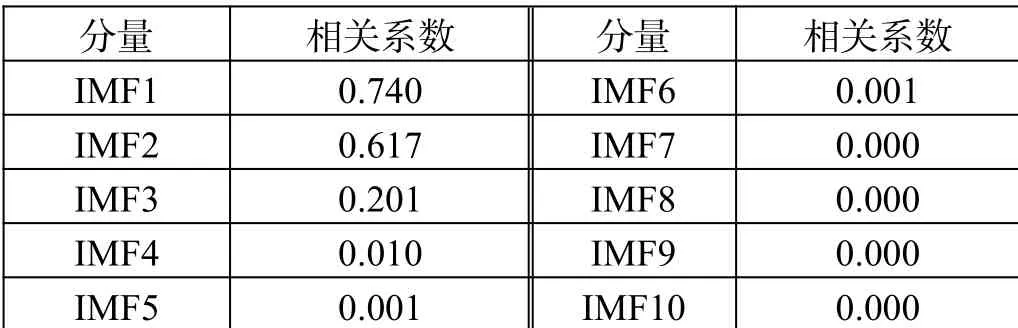
表1 故障電機各階IMF曲線與原信號的相關度

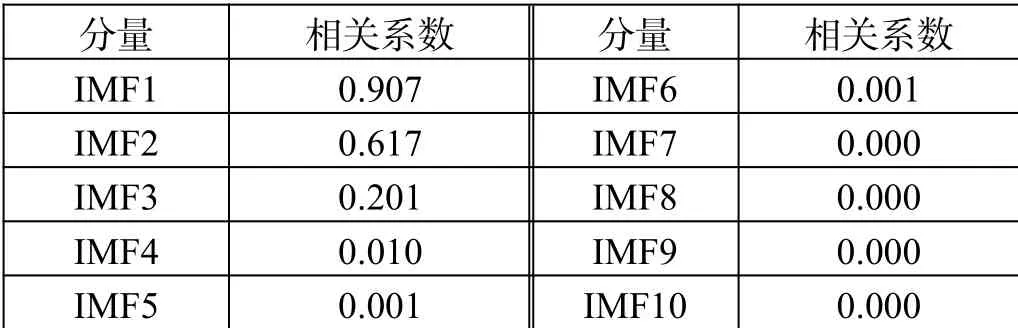
表2 健康電機各階IMF曲線與原信號的相關度

根據公式（5），故障電機的相關系數篩選閾值為0.07，相關系數低于0.07的IMF分量被篩去；同樣，健康電機的相關系數篩選閾值為0.09，相關系數低于0.09的IMF分量為虛假的IMF分量，不能體現原始信號的特點，故在分析IMF分量特征時，應當根據公式（5）舍棄相關系數低于篩選閾值的IMF函數。對篩選后留存的IMF分量，本文提取出以下4個特征[7]：平均瞬時頻率、各層IMF的平均能量各、各層的平均總能量 層IMF能量占比

故障電機和健康電機各階IMF曲線特征提取如表3、表4所示。

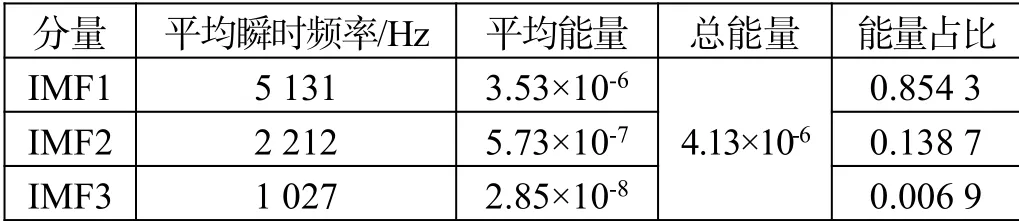
表3 故障電機各階IMF曲線特征提取

表4 健康電機各階IMF曲線特征提取

通過對比故障電機與健康電機所提取的特征，可以得到故障電機振動總能量較小，第二階IMF分量能量占比遠遠比健康電機多，而健康電機振動信號的能量集中在第一階IMF里。圖4—圖7分別為故障電機與健康電機的希爾伯特譜，從圖中可以看到故障電機信號在2 200 Hz處存在沖擊，合理地解釋了故障電機信號在第二階IMF分量中占比高于健康電機的現象。

圖4 故障電機振動信號的希爾伯特譜

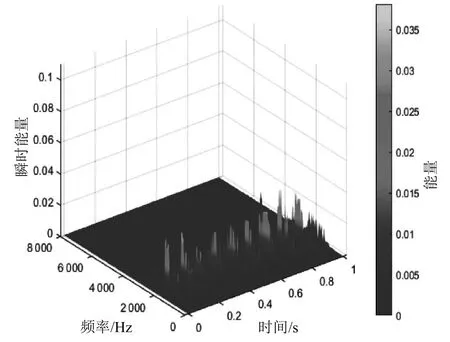
圖5 故障電機振動信號的希爾伯特時頻譜

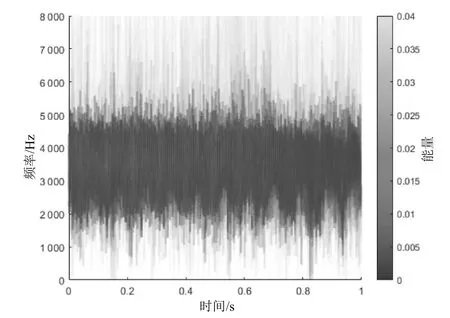
圖6 健康電機振動信號的希爾伯特譜

圖7 健康電機振動信號的希爾伯特時頻譜

相比于故障電機，健康電機的希爾伯特譜則反映出以下特點：①能量分布均勻，集中體現在5 000 Hz左右；②總能量較大，第一階IMF占能量比非常大；③振動沖擊成分較少。

由于希爾伯特譜只能定性地描繪電機的工作狀態(tài)特征，無法進行定量的進行分類，故本文引入了BP神經網絡，對經過EMD分解與IMF分量篩選后的信號根據所選特征進行分類。將所選特征融合為一個十維的特征向量其中為前三階IMF分量平均瞬時頻率；為前三階IMF分量平均能量；Eall為IMF分量的總能量；r=[r1r2r3]，為前三階IMF分量平均能量占總能量比例。以特征向量p作為BP神經網絡的輸入，建立信號分類模型。

3 BP神經網絡進行電機狀態(tài)的分類

BP神經網絡進行分類的過程分為2個階段：第一階段將輸入信息從輸入層經過隱藏層逐層計算輸出；第二階段通過輸出誤差逐漸向前計算各個隱藏層的誤差，根據此誤差修正前一層的權重值[8]。BP神經網絡具有高度自學習和自適應的能力，可以很好地適應后視鏡電機的振動信號分類[9]。建立BP神經網絡，其中隱藏層層數為12，輸出維度為2，如圖8所示。

圖8 BP神經網絡分類模型

該BP神經網絡的數學描述如下：

式（6）—式（9）中：ωij為隱藏層第i個節(jié)點到第j個節(jié)點的權值；xi為輸入層第i個節(jié)點的輸入；θi為隱藏層第i個節(jié)點的閾值；φ為隱藏層的激勵函數；ak為輸出層k個節(jié)點的閾值[9]；φ為輸出層的激勵函數。

本文一共選取了73個樣本信號，包含49段正常電機振動信號、24段故障電機信號，每段信號長度1 s。圖9為BP神經網絡分類的混淆矩陣，在訓練過程中，達到了91.5%的識別率，其中有2個故障樣本被誤判為健康樣本，有3個健康樣本被誤判為故障樣本。在驗證與測試的過程中均達到了85.7%的識別率，整體的BP神經網絡識別率達到了90.4%，基本完成了分類的任務。

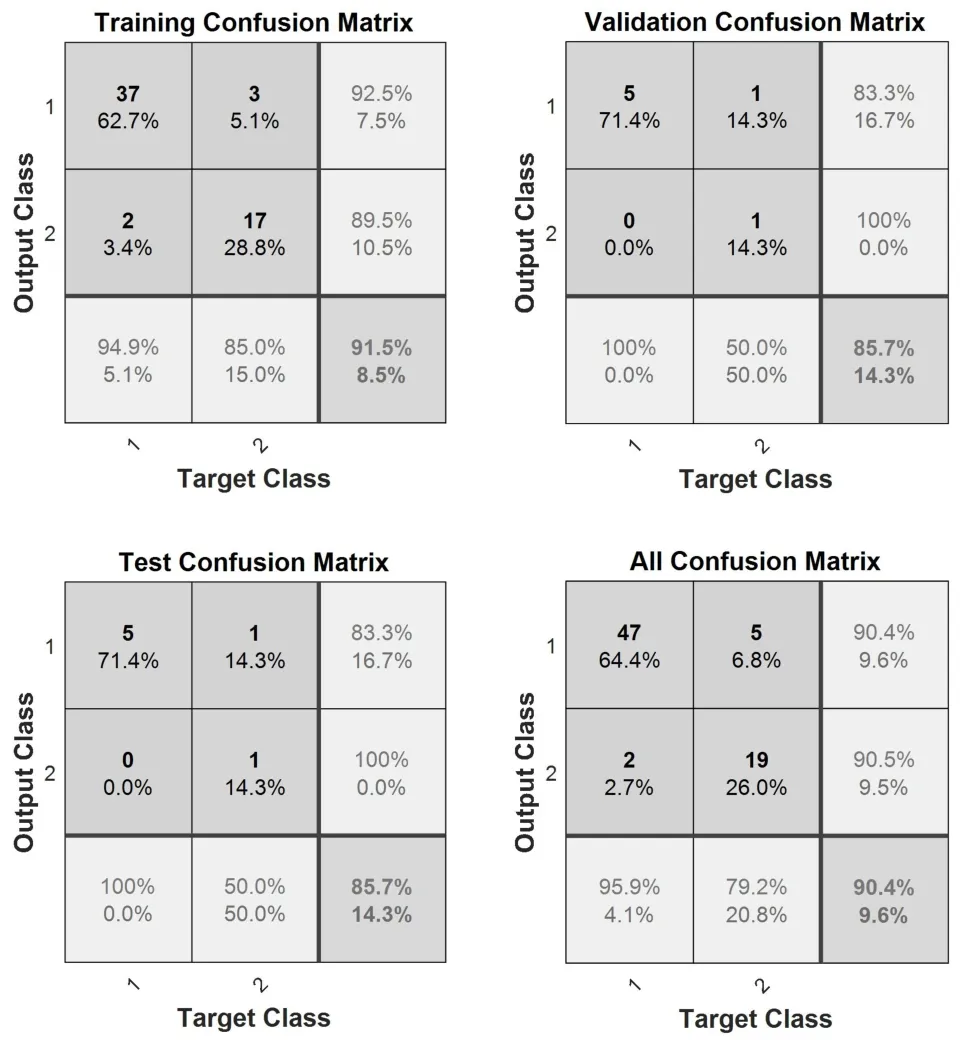
圖9 BP神經網絡分類混淆矩陣

表5為BP神經網絡在測試集中輸出的結果。其中將一個故障樣本誤判為正常的結果，出現該結果的原因可能是該神經網絡的訓練集合樣本數量較少，泛化能力還有提升的空間。但是從結果上分析，該HHT-BP模型已經滿足了故障診斷的準確率要求。

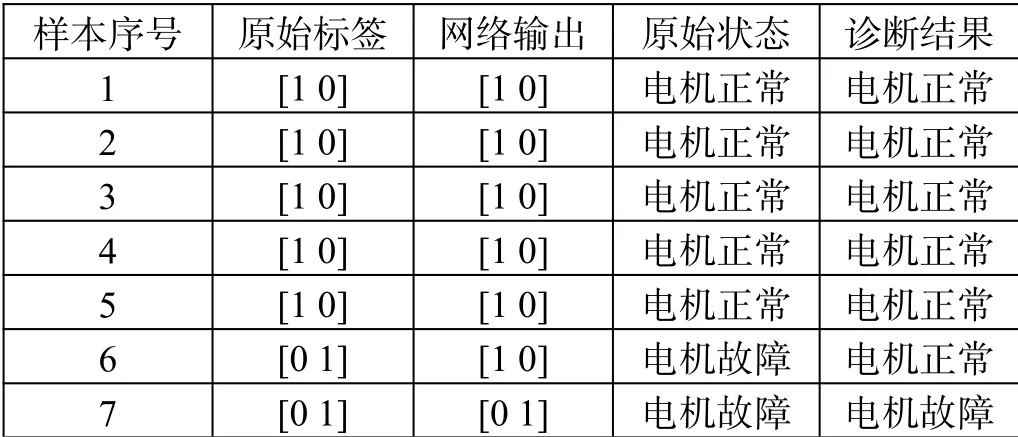
表5 BP神經網絡測試集結果

4 結論

本文所提出的HHT-BP分析模型在處理后視鏡電機振動信號中有良好的成效。通過經驗模態(tài)分解與希爾伯特變換得到振動信號的希爾伯特譜，再根據希爾伯特譜中的信息，提取平均瞬時頻率、平均瞬時能量、總能量、能量占比等10個特征指標。將每一段振動信號提取指標后，將其作為特征向量輸入本文所建立的BP神經網絡分類模型中進行識別。實驗結果表明，該BP神經網絡具有較高的準確識別率，能夠較好地應用于現實檢測環(huán)境中。