基于蒙特卡洛的飛機控制分配魯棒性評估方法

王曉光，尚永爽，杜 軍，賈文銅，史靜平，呂永璽

(1.空軍工程大學航空工程學院，陜西 西安 710038；2.中國人民解放軍93184部隊，北京 100076；3.西北工業大學自動化學院，陜西 西安 710072)

0 引言

隨著現代飛行器設計對于機動性、安全性和可靠性要求的不斷提高，越來越多的飛機舵面可作為主操縱系統的控制面控制飛機的運動[1-2]。對于給定的期望三軸力矩，多操縱面飛機可以有多種組合偏轉形式實現相同的控制目標，針對具有多操縱面配置的飛行器開展多操縱面控制分配技術的研究成為一種必然。

多操縱面布局飛機的控制問題本質上是一個多目標優化問題，如巡航阻力最小、起飛升力最大等[3-4]。目前可用于線性過驅動系統控制分配優化求解的方法可歸納為三類[5-6]：一是廣義逆類分配方法，主要包括：偽逆法、加權偽逆法、再分配偽逆法、多級偽逆法等；二是幾何類分配方法，主要包括：串接鏈法、直接分配法和對邊搜索法等；三是數學規劃類方法，包括：面搜索法、不動點迭代法、有效集法、基于頻域加權的二次規劃法等。

魯棒性是反映控制系統性能優劣的重要指標[7]。為評估不同控制分配方案的優劣，國內外學者經常將系統的魯棒性作為指標來進行控制分配的效果評估。文獻[8]從控制系統魯棒性角度出發，針對多操縱面飛機氣動效能的交叉耦合不確定性，提出了一種基于混合優化的魯棒控制分配策略，建立了魯棒混合優化控制分配模型。文獻[9]針對具有冗余執行機構的過驅動系統，在考慮控制效率不確定性的條件下，提出了一種基于魯棒優化理論的控制分配算法，有效降低了控制效率不確定性的影響，使分配結果更為合理，一定程度上提高了控制分配算法的魯棒性，改善了飛控系統的性能。文獻[10]基于廣義逆控制的飛控系統，分析了控制系統的不確定性以及在控制效能矩陣存在不確定性時的飛控系統魯棒性問題。文獻[11]針對一類具有不確定時變參量的線性參變過驅動系統的控制分配問題，考慮系統的不確定參量擾動和執行器物理約束，建立了含有時變不確定因子的控制分配優化模型，并根據魯棒優化思想，采用矢量變換技術處理時變不確定因子，得到了一種基于有約束錐二次凸優化模型的魯棒控制分配算法，實現對過驅動系統偽控指令的在線優化分配。文獻[12]針對無人機廣泛采用先進操縱面帶來的控制分配問題，提出了基于閉環廣義逆的魯棒控制分配新方案，在基于廣義逆的控制分配方法基礎上，加入了控制量對應狀態的反饋，分析了該方案的可行性。同時，魯棒控制分配方法也在國內外航天、航海等其他領域有所應用[13-15]。

然而，上述文獻均是針對不同的控制分配方法，從不同的角度出發評估某一特定控制分配方法的魯棒性，很難適用于其他控制分配方法。因此，有必要構建一種通用的多操縱面飛機控制分配魯棒性評估方法，為過驅動系統的控制分配效果提供較為統一的評價準則。基于此思路，本文給出了一種通用的基于蒙特卡洛方法的控制分配魯棒性評估框架；建立了過驅動系統的控制分配方法魯棒性評估函數；對偽逆法、串接鏈法和面搜索法三種典型的分配方法進行了仿真驗證，并給出了結論。

1 魯棒性評估思路和框架

對飛機飛行品質的評估是基于飛機飛行控制律進行的，評估需考慮的不確定性包括：質量數據的不確定性、系統輸入量的不確定性、氣動數據庫的不確定性等。其一般實現過程：在考慮上述不確定性的情況下，設計出控制律之后，通過隨機模擬的方法對飛機的一些特征量(氣流角、位置、被控量的調節時間和超調量等)進行統計分析，來獲得控制律在不確定參數下魯棒性能的量化值。但過驅系統分配方法魯棒性的研究，有別于已有控制律的飛行品質評估[16]。由于過驅系統的設計目的是將期望的三軸力矩系數合理地分配到各個舵面，因此在研究過驅系統的參數不確定時只需考慮舵面效率的不確定性。對于線性過驅系統分配方法的魯棒性研究是基于控制效能矩陣中參數的不確定性。

本文針對過驅系統分配方法進行魯棒性評估的基本思想：考慮舵面效率的不確定性范圍，根據魯棒性要求的精度和置信度確定最小仿真次數；基于蒙特卡洛方法[17]進行隨機模擬仿真獲得實際三軸力矩系數，建立過驅系統分配方法魯棒性的評估函數；針對不同的分配方法求得魯棒性能量化值，進而可以比較分析各個方法魯棒性的優劣。

進行過驅系統分配方法魯棒性評估的具體步驟如下：

1) 確定控制效能矩陣中參數的不確定性范圍；

2) 由給定精度和置信因子確定最小仿真次數，并且產生滿足分布的控制效能矩陣參數的隨機數；

3) 建立過驅系統分配方法魯棒性評估指標函數；

4) 進行多次仿真，獲得仿真結果后進行參數概率統計分析，依據魯棒性評估指標函數驗證控制分配算法的魯棒性；

5) 比較不同控制分配方法的魯棒性，為控制分配方法的選擇提供依據。

過驅系統分配方法的魯棒性研究驗證過程如圖1所示。

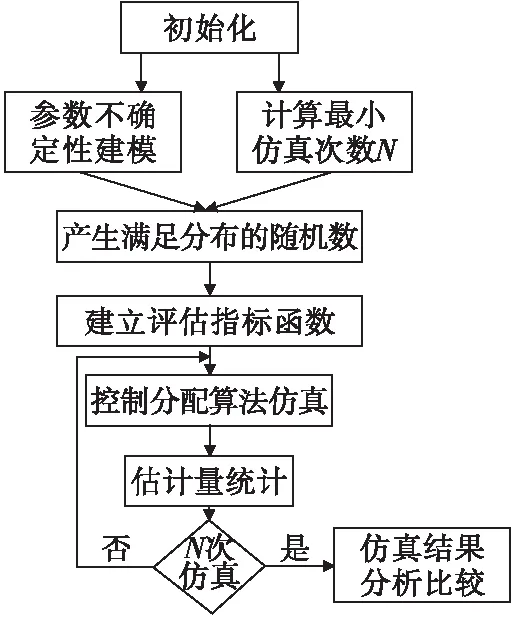
圖1 基于蒙特卡洛的過驅系統分配方法魯棒性驗證框圖Fig.1 Robustness verification diagram of overdrive system’s control allocation method based on Monte-Carlo

2 過驅系統分配方法魯棒性評估指標函數

2.1 相關概率統計基礎

2.1.1 3σ原則

對于分布為N(μ,σ2)的隨機變量x，數值分布在(μ-3σ,μ+3σ)中的概率為0.997 3，可以認為正態隨機變量的取值在(μ-3σ,μ+3σ)區間內，這就是所謂的3σ原則。在參數不確定性建模時，采用3σ原則能保證構成參數不確定項的隨機變量基本可以限定在3σ分布范圍內，從而避免因為參數值出界而導致的系統不穩定。

2.1.2 最小仿真次數確定方法

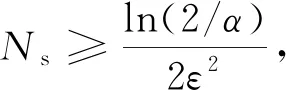
2.1.3 均值和方差的估計值計算

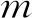
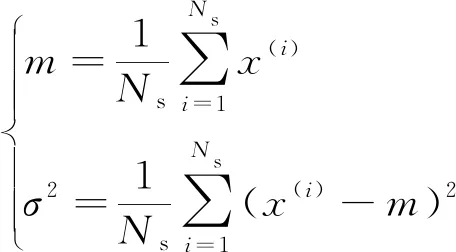
(1)

當樣本數量足夠多時，樣本均值的置信區間為：

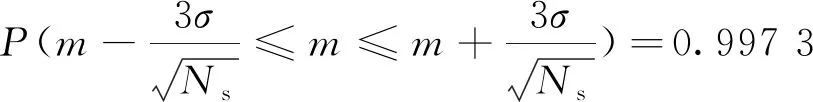
(2)

2.2 魯棒性評估指標函數的建立

過驅系統分配方法的實質是按照一定的指標要求將期望的三軸力矩系數合理地分配到各個舵面上去，其最基本的要求是分配系統的實際三軸力矩系數能夠跟蹤上期望的三軸力矩系數，如圖2所示。

圖2 分配系統的基本框圖Fig.2 Basic block diagram of the allocation system

對于過驅系統分配方法魯棒性的評估也是針對實際三軸力矩系數和期望三軸力矩系數之間的差別來入手。對于給定的三軸期望力矩系數，在控制效能矩陣參數存在不確定性的情況下進行N次仿真后，可求出實際三軸力矩系數的均值和方差值，并且可以確定均值相應的置信區間，根據這些統計信息便可以評估在給定的三軸期望力矩系數下分配方法的魯棒能力。

具體在仿真驗證過程中，采取下式所示的性能評估函數

(3)

式(3)中，Vcl、Vcm、Vcn分別為實際的滾轉力矩系數、實際的俯仰力矩系數和實際的偏航力矩系數；Vdcl、Vdcm、Vdcn分別為期望的滾轉力矩系數、期望的俯仰力矩系數和期望的偏航力矩系數；k是評估指標系數，是一個無量綱量，它反映了評估函數對實際輸出的力矩系數和期望的力矩系數二者之間的差別要求。k的選用原則是結合飛機舵面效率的不確定性，以盡可能清晰、準確地體現控制分配方法的魯棒性。如果指定了k的值，則可以在仿真中記錄滿足性能評估標準要求的次數n，顯然，0≤n≤N。n的大小代表了在評估指標系數k下分配方法的魯棒性，n值越大則說明在評估指標系數k下該分配方法的魯棒性越強，反之亦然。因此控制分配方法魯棒性的優劣還可以表現在累積頻數曲線中。

3 魯棒性驗證

一般來說，線性過驅動系統可描述為：假設控制變量為u(t)∈Rm1，期望的虛擬變量是v(t)∈Rm2，線性過驅動系統的分配問題就是在給定v(t)及映射Be:Rm1→Rm2(m1>m2)的情況下，求解不定方程Beu(t)=v(t)，使u(t)在不超出約束Ω的情況滿足一定的性能指標。

從數學描述上看，線性過驅動系統的分配求解問題是一個受約束的線性方程組求解問題，由于控制變量的維數大于虛擬變量的維數，分配問題的解有三種情況：多解、唯一解、無解。從數學映射關系上分析，線性過驅動系統的分配問題求解是根據映射Be:Rm1→Rm2(m1>m2)找到一種反映射，使解不超出約束；并且這種反映射還可能包含其他系統性能指標。這些指標在保證等式約束Beu(t)=v(t)的同時，還使線性過驅動系統的分配求解與工程設計的需求相匹配。

以Admire多操縱面飛機為例，在馬赫數為0.4，高度為3 000 m的狀態點下得到控制效能矩陣：

將Be作為標稱效能陣，同時選取精度ε=0.05，置信因子α=0.04，結合最小仿真次數的計算公式，得到最小仿真次數Ns≥782.4，故可取仿真次數N=800，對于控制效能矩陣中的任意參數bij，設定每個舵面舵效值的不確定性為50%。在此基礎上進行控制分配方法魯棒性評估驗證，評估驗證過程中涉及控制分配方法的具體步驟詳見文獻[18]。

3.1 偽逆分配方法的魯棒性評估

給定期望的三軸力矩系數：

vd=[0.03 0.3 -0.03]。

(4)

進行N次蒙特卡洛仿真后得到偽逆法對應的實際無量綱三軸力矩系數曲線如圖3所示。

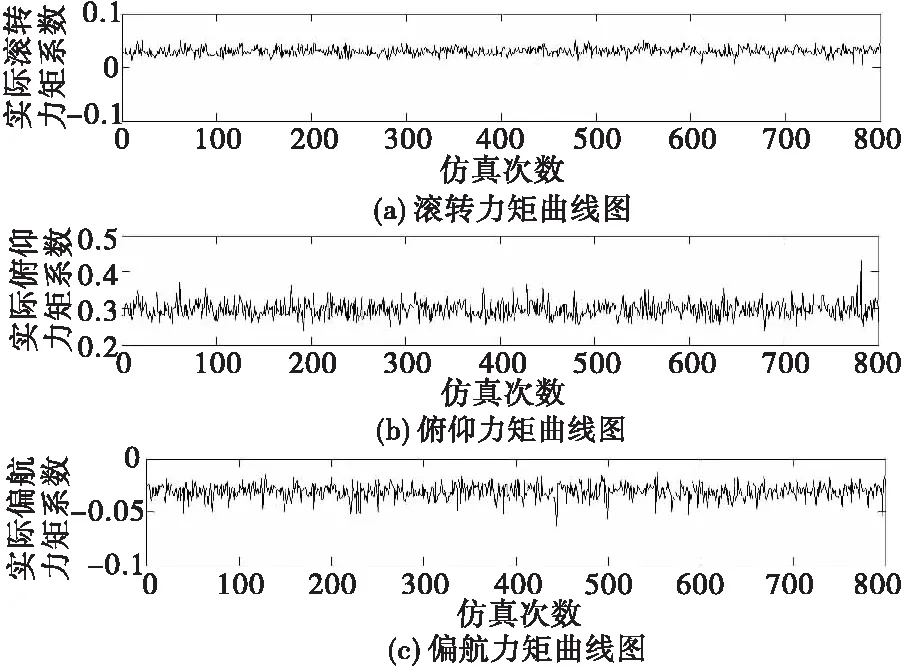
圖3 控制效能矩陣不確定時的偽逆法三軸力矩系數Fig.3 Triaxial torque coefficients of pseudo inverse method for uncertain control efficiency matrix

統計得到實際三軸力矩系數的均值與標準差，并求其對應的樣本均值置信區間，結果如表1所示。

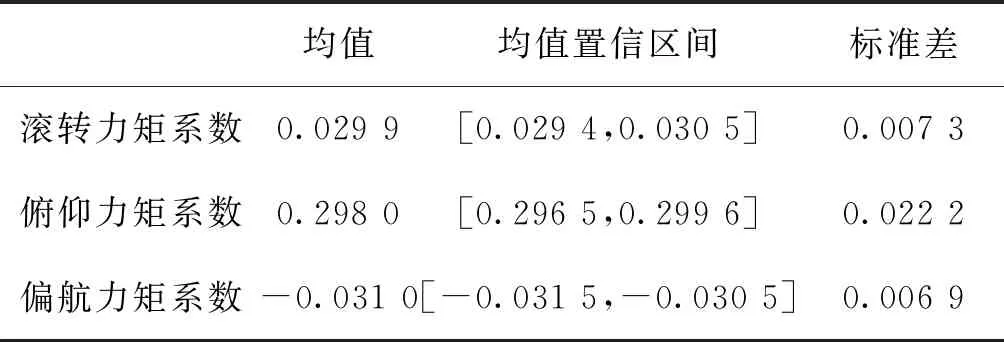
表1 偽逆法仿真結果統計Tab.1 Simulation result statistics for pseudo inverse method

結合圖3和表1來看，在舵面效率存在50%的不確定性時，通過蒙特卡洛仿真驗證可知，實際的三軸力矩系數均在期望三軸力矩系數附近，偽逆法對于舵效的不確定性具有一定的魯棒性。

偽逆分配法考慮控制效能矩陣不確定時的累積頻數曲線如圖4所示。

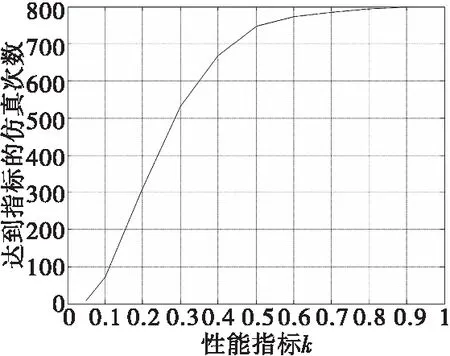
圖4 控制效能矩陣不確定時的偽逆法累積頻數曲線Fig.4 Frequency accumulating curve of pseudo inverse method for uncertain control efficiency matrix

考慮舵效值的50%不確定性，結合圖4可知，當評估指標系數k=0.5時，達到指標的仿真次數為752，也就是說此期望狀態下對于控制效能矩陣參數的不確定性，偽逆法得到的實際三軸力矩系數值與期望三軸力矩系數之差有94%的概率不超過期望三軸力矩系數的一半。

3.2 串接鏈分配方法的魯棒性評估

給定期望的三軸力矩系數vd不變，進行N次蒙特卡洛仿真后得到串接鏈法對應的實際無量綱三軸力矩系數曲線如圖5所示。

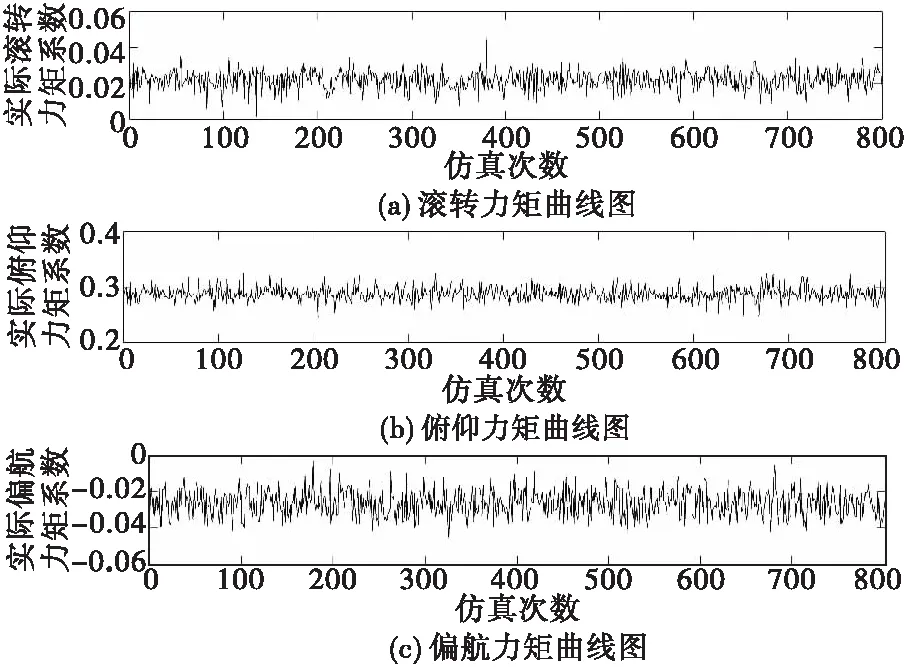
圖5 控制效能矩陣不確定時的串接鏈法三軸力矩系數Fig.5 Triaxial torque coefficients of daisy chain method for uncertain control efficiency matrix

統計N次蒙特卡洛仿真后實際三軸力矩系數的均值與標準差，求得其對應的均值置信區間，如表2所示。

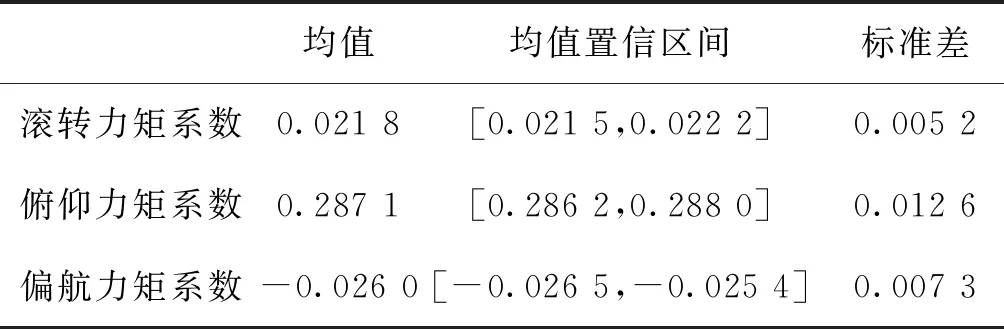
表2 串接鏈法仿真結果統計Tab.2 Simulation result statistics for daisy chain method

結合圖5和表2中數據來看，在舵面效率存在50%的不確定性時，同偽逆法相比，串接鏈法均值離期望力矩系數較遠，且期望的三軸力矩系數在均值置信區間之外，說明仿真得到的力矩系數與期望力矩系數差別較大；標準差總體上比偽逆法大，說明仿真結果分布較為分散。因此，從仿真統計結果分析，可以認為該方法在舵面效率存在50%的不確定性時魯棒性比偽逆法差。

串接鏈分配方法考慮控制效能矩陣不確定時的累積頻數曲線如圖6所示。

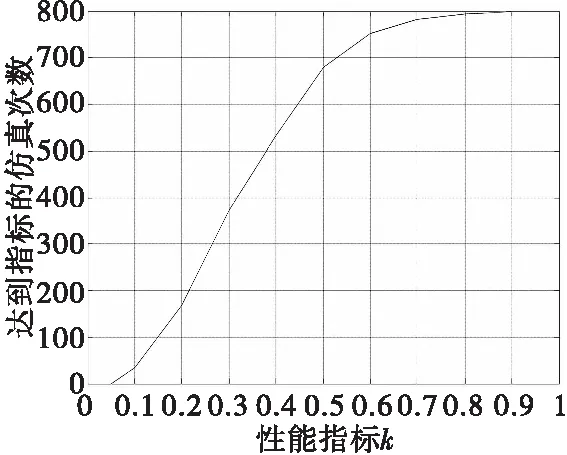
圖6 控制效能矩陣不確定時的串接鏈法累積頻數曲線Fig.6 Frequency accumulating curve of daisy chain method for uncertain control efficiency matrix

考慮舵效值的50%不確定性，結合圖6可知，當k=0.5時，此期望狀態下對于所有的控制效能矩陣參數的不確定性，串接鏈法達到指標的仿真次數為679，也就是說此期望狀態點下對于控制效能矩陣參數的不確定性，串接鏈法得到的實際三軸力矩系數值與期望三軸力矩系數之差有84.88%的概率不超過期望三軸力矩系數的一半。總體來說，串接鏈法對于舵效不確定性的魯棒性比偽逆法差。

3.3 面搜索分配方法的魯棒性評估

給定期望的三軸力矩系數vd不變。進行N次蒙特卡洛仿真后得到面搜索法對應的實際無量綱三軸力矩系數曲線如圖7所示。

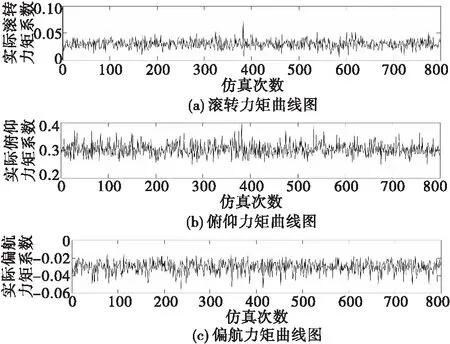
圖7 控制效能矩陣不確定時的面搜索法三軸力矩系數Fig.7 Triaxial torque coefficients of surface search method for uncertain control efficiency matrix

統計N次蒙特卡洛仿真后實際三軸力矩系數的均值與標準差，并求其對應的均值置信區間如表3所示。

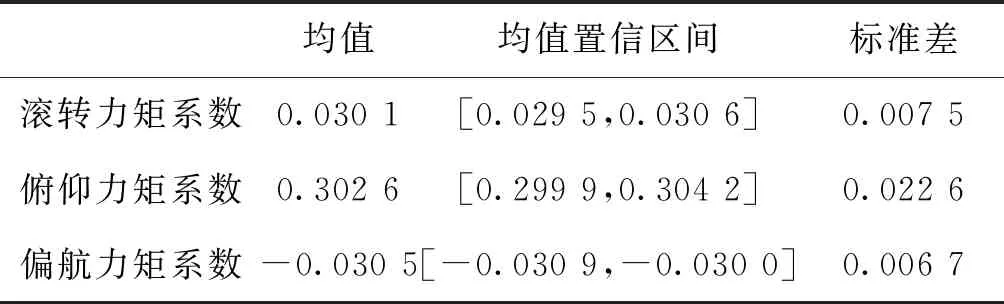
表3 面搜索法仿真結果統計Tab.3 Simulation result statistics for surface search method

結合圖7和表3來看，在舵面效率存在50%的不確定性時，通過蒙特卡洛仿真驗證可知，面搜索法計算得到的三軸力矩系數均值在期望三軸力矩系數附近，且期望的三軸力矩系數均在均值置信區間之內，說明面搜索法仿真得到的力矩系數與期望力矩系數差別不大，面搜索法對于舵效的不確定性具有一定的魯棒性。但該方法的仿真結果統計中標準差總體上稍大，說明該方法的仿真結果分布較散。

考慮控制效能矩陣不確定時的累積頻數曲線如圖8所示。

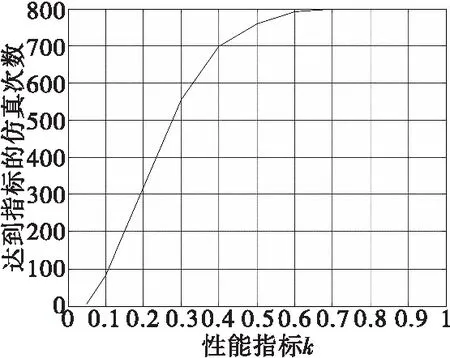
圖8 控制效能矩陣不確定時的面搜索法累積頻數曲線Fig.8 Frequency accumulating curve of surface search method for uncertain control efficiency matrix

考慮舵效值的50%不確定性，結合圖8可知，k=0.5時，此期望狀態下對于所有的控制效能矩陣參數的不確定性，面搜索法達到指標的仿真次數為758，也就是說此期望狀態點下對于控制效能矩陣參數的不確定性，面搜索法得到的實際三軸力矩系數值與期望三軸力矩系數之差有94.75%的概率不超過期望三軸力矩系數的一半，優于偽逆法和串接鏈法。

總體來說，通過綜合對比仿真結果統計和累積頻數曲線可以發現：與前兩種方法相比較，面搜索方法的魯棒性最強。究其原因在于面搜索法的分配效率最高，在分配時能夠最大限度達到轉矩可達集邊界，進而當控制效能矩陣存在不確定時能夠體現較強的魯棒性。

4 結論

本文提出一種多操縱面飛機控制分配的魯棒性評估方法，在建立魯棒性評估指標函數的基礎上，基于蒙特卡洛方法，進行了數值計算仿真，對偽逆、串接鏈和面搜索三種控制分配方法進行了魯棒性評估。仿真結果表明，該方法可以有效實現控制分配方法的魯棒性評估，具有較好的通用性和較高的評估準確度，能夠為控制分配的性能評估提供有效的技術支撐和參考。仿真結果顯示，在控制效能矩陣存在50%不確定性的情形下，面搜索法的魯棒性能最好，偽逆法次之，串接鏈法的魯棒性能最差。